钢桁腹式混凝土组合箱梁的扭转效应分析
杨霞林, 于小芹, 张元海
(1.兰州交通大学 土木工程学院,兰州 730070; 2.山东省建筑工程质量检验检测中心有限公司,济南 250031)
1 引 言
钢桁腹式混凝土组合箱梁是一种较新型的钢-混组合箱梁结构,具有现场施工便捷、自重轻、避免腹板开裂、通透性好以及桥型优美等优点。我国已有的该种桥型最为典型的是南京江山桥,已建成的该种桥型还有国道107宝安段匝道以及水碾堡特大桥。目前,国内外学者对该类结构的受力特点进行了较为深入的研究与探索,但关于扭转性能方面的研究涉及很少[1-5],王彤等[6]利用换算薄壁箱梁法思想及箱梁结构理论,提出了桁腹式组合桁架弯曲变形、扭转和畸变的计算方法。国内外对其他类型的钢-混组合箱梁的扭转性能研究比较成熟[7-9],故本文以薄壁箱梁扭转理论为基础,结合现有钢-混组合箱梁的扭转研究方法对钢桁腹式混凝土组合箱梁进行扭转效应的初步探究。
首先,按照剪切变形相等的原则将不连续钢桁腹杆转化为连续的薄壁混凝土腹板,并推导其各项扭转几何特性值。然后,基于薄壁箱梁扭转理论,推导出组合箱梁闭口断面的混凝土顶底板和换算钢腹板的扭转翘曲应力表达式,进而推导出组合箱梁约束扭转控制微分方程;利用初参数法求解微分方程,并分析出翘曲双力矩以及扭转翘曲正应力随梁跨的变化规律。最后,通过有限元模拟分析,将有限元值和理论值进行比较,以验证理论计算方法的可靠性与准确性。
为便于开展相应的分析与研究,本文引入以下基本假定。 (1) 斜腹杆为二力杆,仅承受轴力,不考虑失稳; (2) 上部荷载作用下的弯矩由顶底板承担,腹杆仅承受剪力且受力均匀; (3) 组合箱梁在偏载作用下发生扭转时,忽略钢桁腹杆自身的扭转; (4) 符合小变形假定,且各个杆件的受力均在弹性范围内; (5) 横断面的纵向应力分布符合拟平截面假定。
2 钢桁腹杆纵向表观弹性模量
由于钢桁腹式混凝土组合箱梁的腹杆不连续,且腹杆与混凝土顶底板材料不一致,因此需要先求解钢桁腹杆的纵向表观弹性模量。
相邻两腹杆相接节点通过剪力键钳固于混凝土承托中,因此混凝土翼板所受的力能够平顺地传递到钢桁腹杆,可将混凝土顶底板之间的钢桁腹杆看作连续折线。任取一组折线单元如图1所示,每组折线单元以两个弯矩零点为界限[3]。
利用图乘法计算单元在轴向力作用下的纵向变形Δ1。图2为乘法受力图。

图1 腹杆折线单元

图2 腹杆折线单元受力
折线单元纵向变形Δ1为
(1)
式中E0为钢桁腹杆初始弹性模量(即钢材弹性模量),I0为钢桁腹杆截面惯性矩,A0为钢桁腹杆截面面积,P为钢桁腹杆所受轴力,h为钢桁腹杆竖向高度,θ为相邻两钢桁腹杆之间的夹角。
取一块等效平钢板代替钢桁腹杆[6],假设此平钢板厚度为ts,则
ts=E0/Gs·(A0hm/L3)
(2)
式中Gs为钢材剪切模量,m为折线单元纵向长度的一半,L为钢桁腹杆长度。
在作用力P作用下,等效平钢板的纵向位移为
(3)
式中Ex为钢桁腹杆纵向表观弹性模量,As为等效钢腹板的截面积。
由Δ1=Δ2,联立式(1~3),得钢桁腹杆纵向表观弹性模量Ex为
(4)
3 扭转荷载分解
图3所示为钢桁腹式混凝土组合箱梁的横断面,断面上作用有竖向偏载时会发生扭转变形,一般而言,将该偏心荷载分解为一对对称荷载与一对反对称荷载[10]。组合箱梁在反对称荷载作用下,截面会产生刚性扭转与畸变变形。为阻止组合箱梁截面发生畸变变形,在截面施加一虚拟的对角支撑,使其只发生刚性扭转变形[9],如图3所示。
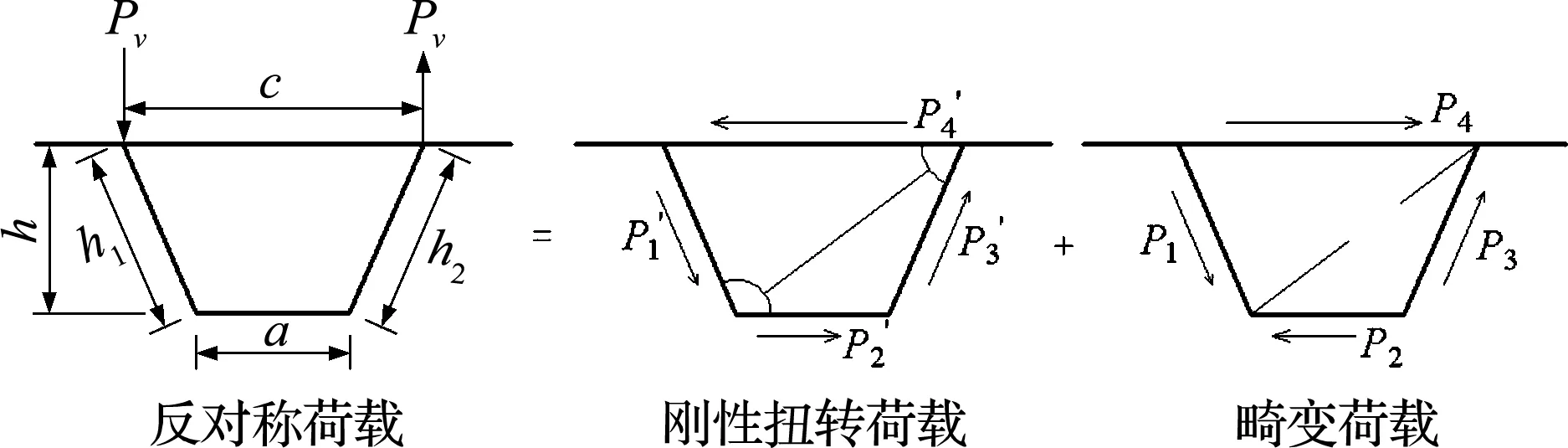
图3 反对称荷载的分解
根据静力平衡条件,得扭转荷载为[11]
(5)

4 钢桁腹式混凝土组合箱梁的扭转分析
4.1 扭转几何特性
分析钢桁腹式组合箱梁的约束扭转翘曲应力,需先计算钢桁腹式组合箱梁的截面扭转几何特性(包括扭心、辅助扇性坐标、主扇性坐标、主扇性惯性矩、主扇性静矩和广义扇性静矩)。
图4的点1为混凝土顶板与钢桁腹杆交接处参考计算点,点2为顶部翼缘板端部参考计算点,点3为底板与钢桁腹杆交接处参考计算点。辅助极点选取顶板中心点B处,计算控制点1,2和3辅助扇性坐标ωB、主扇性坐标ωA、主扇性静矩Sω以及扭心位置R和主扇性惯性矩Iω。各参数(宽度、厚度和倾角)均在图4中标明。
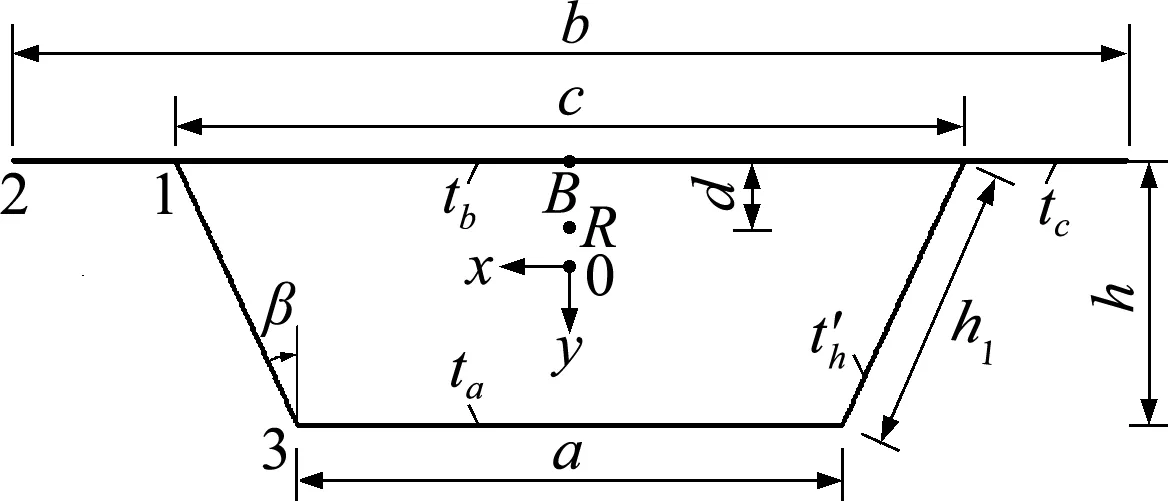
图4 钢桁腹式混凝土组合箱梁截面
点1,2和3的辅助扇性坐标表达式为
(6)

扭心R到顶板中心的距离d为
d=-Iω B x/Iy=h/[a3ta+c3tb+(b3-c3)tc+
(7)
式中Iω B x为辅助扇性坐标图与x坐标图图乘所得,Iy为组合箱梁截面对x轴的惯性矩,
点1,2和3的主扇性坐标表达式为
(8)
主扇性惯性矩可通过将主扇性坐标图自乘求得,
(9)
式中nc为混凝土弹性模量与钢桁腹杆纵向表观弹性模量之比,即nc=Ec/Ex。
主扇性静矩计算式为
(10)
4.2 自由扭转
组合箱梁横断面扭转变形的截面位移可以表示为[10]
(11)
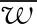
根据式(11),可得组合箱梁横截面的正应力和剪应力为

(12a)

(12b)
式中v为泊松比。
纯扭转翘曲位移为
(13)

组合箱梁的自由扭转微分方程为
(14)
式中Mz为集中扭矩,mz为分布扭矩,Id为扭转惯性矩。
(15)
式中mG=Gc/Gs,式(15)表示若将换算钢腹板进一步等效换算为混凝土腹板,可将其按混凝土薄壁箱梁计算Id。Id通常由闭口箱室与开口悬臂板迭加求得[12],而在计算组合箱梁的Id时,开口部分的扭转刚度很小,为计算简便,一般忽略不计。
4.3 约束扭转
根据薄壁箱梁设计理论,需要引入位移量β′(组合箱梁翘曲位移自由度)对翘曲位移计算进行修正,使得组合箱梁发生约束扭转后仍能保持变形后的连续。
翘曲位移表达式为
(16)
翘曲正应力的表达式可以表示为
(17)

对于钢桁腹式混凝土组合箱梁,顶底板和换算钢腹板由于其材料不同,各自翘曲正应力计算式也不相同。
混凝土翼板约束扭转正应力计算式为
(18)
式中Ec为混凝土的弹性模量。
换算钢腹板的扭转翘曲正应力计算式为
(19)
式中Ex为钢桁腹杆的纵向表观弹性模量。
翘曲正应力σω对应的翘曲双力矩Bω是一对大小相等方向相反的力矩,计算式为
(20)
式中Iω为主扇性惯性矩,
(21)
式中A1,A2和A3为混凝土顶板和底板截面面积以及换算腹板截面面积。
由式(18~20),翘曲正应力表示为
(22)
约束扭矩Mz可由翘曲双力矩Bω表示为
(23)
5 约束扭转微分方程及其参数解
5.1 约束扭转微分方程
双力矩Bω、扭矩Mz以及翘曲正应力σω的求解需要先求出挠曲变形系数β′,然后通过β和θz的关系求解θz。
截面总扭矩为
(24)

根据式(24)可得β和θz的关系为
(25)
(26)
Mz为集中扭矩,mz为分布扭矩,两者之间的关系为
dMz/dz=-mz
(27)
对式(26)求导并联立式(27),经整理得β的微分方程为
(28)

同理可推导出θz的微分方程为
(29)
5.2 初参数法求解微分方程
规定z=0处,四个初参数中θ0为该处角位移,β′0为翘曲位移,Bω 0为扭转翘曲双力矩,M0为扭矩,微分方程的齐次方程的通解为
θz=C1+C2z+C3sinhkz+C4coshkz
(30)
(31)
Bω=-GId(C3sinhkz+C4coshkz)
(32)
Mz=C2GId
(33)
初参数解为
(34)
(35)
(36)
Mz=M0
(37)
在式(34~37)中,组合箱梁的边界条件决定4个初参数的取值,初参数解适用于无外界荷载作用下的组合箱梁,一般而言,对于作用有外荷载的组合箱梁,应在初参数解的基础上补充相应的影响项。
如图5所示,当组合箱梁跨内有扭矩时,式(34~37)分别为
(38)
(39)
(40)
(41)
式中符号=a表示只有z>a时的数值才计入算式,同样=b表示只有z>b时的数值才计入算式,当z>c时,对应的积分上限也会发生改变。
5.3 边界条件
边界条件不同,角位移θz以及挠曲变形系数β′的取值也不相同[13]。
(1) 固定端θz=0,β′=0
(2) 简支端θz=0,β″=0
5.4 作用集中扭矩的简支组合箱梁扭转分析
在简支组合箱梁中,距梁端a处作用一集中扭矩,如图6所示,根据边界约束条件θz=0,β′=0,z=0时,θz=0,Bω 0=0,可得微分方程解为
当z (42) 当z≥a时, Mz=-(a/l)T (43) 图6 简支组合箱梁作用集中扭矩 以某钢桁腹式混凝土组合箱梁简支梁为例[14],其上部结构采用单跨(35 m)等截面钢桁腹式预应力混凝土组合箱梁结构,主梁为单箱单室截面,顶板宽8.5 m,底板宽4.8 m,梁高2.3 m。混凝土板采用C50混凝土,弹性模量为3.45×104MPa,钢桁腹杆采用Q345C级钢管,规格为Φ351×16,钢桁腹杆水平倾角为67° 左右,节间距为1.95 m。组合箱梁横断面和纵断面分别如图7和图8所示。为简化计算,分别将顶板和底板的板厚均分,将钢桁腹杆转换成薄壁混凝土腹板,横断面简化为如 图9 所示截面。按上述理论推导式(6~10)和式(15)求得扭转几何特性,结果见表1及图10~图13。 图7 组合箱梁横断面(单位:m) 图8 组合箱梁纵断面(单位:m) 图9 组合箱梁计算模型及横向加载位置(单位:mm) 表1 扭转几何特性 图10 辅助扇性坐标ωB(单位:m2) 图11 主扇性坐标ω(单位:m2) 图12 主扇性静矩单位:m4) 图13 广义扇性静矩单位:m4) 依据《公路桥规》[15]中车道荷载的情况对该桥施加P=330 kN的偏载,偏心距e=2075 mm,不计桥梁自重。横向加载如图14所示。 以此算例为研究对象,探究翘曲双力矩随着集中扭矩分别作用在简支钢桁腹式混凝土组合箱梁上l/4和3l/4跨以及跨中截面处的变化,图15所示为翘曲双力矩沿梁纵向的变化曲线。可见,翘曲双力矩在集中扭矩作用处达到最大值,并且衰减速度相当快,距离集中扭矩作用处越远,翘曲双力矩就越小,梁端处为0。 以跨中作用集中扭矩为例,绘出点1(左侧腹杆与混凝土顶板交点)、点2(混凝土顶板左端点)与点3(左侧腹杆与混凝土底板交点)翘曲正应力沿梁纵向的变化曲线,如图16所示,图中应力以拉为正,以压为负。集中扭矩作用处的翘曲双力矩很大,使得该处组合箱梁截面产生了很大的翘曲应力,而距离集中扭矩作用处越远,组合箱梁的翘曲双力矩越小,翘曲正应力也越小,梁端处为0。 图14 横向加载位置 图15 翘曲双力矩沿梁纵向的变化曲线 图16 扭转翘曲正应力沿梁纵向的变化曲线 为验证以上理论计算方法的可靠性与准确性,运用ANSYS进行有限元数值模拟计算,并进一步与理论计算结果进行对比分析。有限元模型横向和纵向尺寸构造如图7和图8所示,选用SOLID185单元模拟顶板和底板,BEAM188单元模拟钢桁腹杆[16],不考虑腹杆与混凝土的相对滑移,钢桁腹杆与混凝土板的刚性连接通过建立约束方程进行自由度耦合。简支钢桁腹式混凝土组合箱梁的边界一端为活动铰支座,约束梁的竖向和横向位移,另一端为固定铰支座,约束梁的竖向和纵向和横向位移。模型的相关数据列入表2。腹杆倾斜的角度为67° 左右,两相邻腹杆的最大距离为1.95 m。对该模型跨中截面处施加如图17所示的一对反对称荷载,使其满足仅表现出扭转与畸变的叠加效应,而不包含弯曲效应。 根据上述所推导的理论计算方法求取算例中钢桁腹式混凝土组合箱梁的跨中截面处和0.1l跨截面处1点(腹杆与顶板连接点)、2点(顶板左端点)以及3点(腹杆与底板连接点)的扭转翘曲正应力,叠加畸变翘曲正应力(计算过程本文略)后与有限元计算结果进行比较,列入表3。 图17 反对称荷载施加 表2 有限元模型的相关参数 表3 翘曲正应力有限元数值与理论数值的对比(单位:kPa)Tab.3 Comparison between finite element value and theoretical value(unit:kPa) 由表3可知,有限元数值与本文方法计算的理论数值相差并不大,差值百分比在10%以内,可见本文计算方法合理可行。 (1) 通过选取合适的辅助极点,推导出组合箱梁横截面辅助扇性坐标ωB、扭心R、主扇性坐标ωA、主扇性惯性矩Iω及主扇性静矩Sω等扭转几何特性表达式,并通过算例求解出扭转几何特性值,绘出辅助扇性坐标图、主扇性坐标图、主扇性静矩以及广义扇形静矩图。 (2) 对钢桁腹式混凝土组合箱梁进行自由扭转与约束扭转分析,推导出组合箱梁约束扭转微分方程,并通过初参数法求解出转角、翘曲位移、扭转翘曲双力矩以及扭矩的一般公式,以跨中作用集中扭矩的简支组合箱梁为例,赋予边界条件,求解出四个参数的表达式。 (3) 根据算例,分析翘曲双力矩以及扭转翘曲正应力随梁跨变化,翘曲双力矩在集中扭矩作用处达到最大值,并且衰减速度很快,使得该处箱梁截面的翘曲应力达到最大值,箱梁的翘曲双力矩在远离集中扭矩作用处几乎为0,翘曲正应力也几乎为0。 (4) 建立有限元模型施加荷载并求解出翘曲正应力,利用本文所述方法求取跨中截面和0.1l跨截面点1,2和3的扭转翘曲正应力,与畸变翘曲正应力叠加后与有限元值作比较,结果表明有限元数值与本文方法计算的理论数值差值百分比在10%以内,可见本文推导的理论计算方法合理可行。 (5) 本文没有考虑预应力对扭转效应的影响,实际工程中钢桁腹式混凝土组合箱梁常在上下翼板布置预应力筋,故需进一步研究预应力产生的扭转效应。

6 算例分析
6.1 扭转几何特性计算






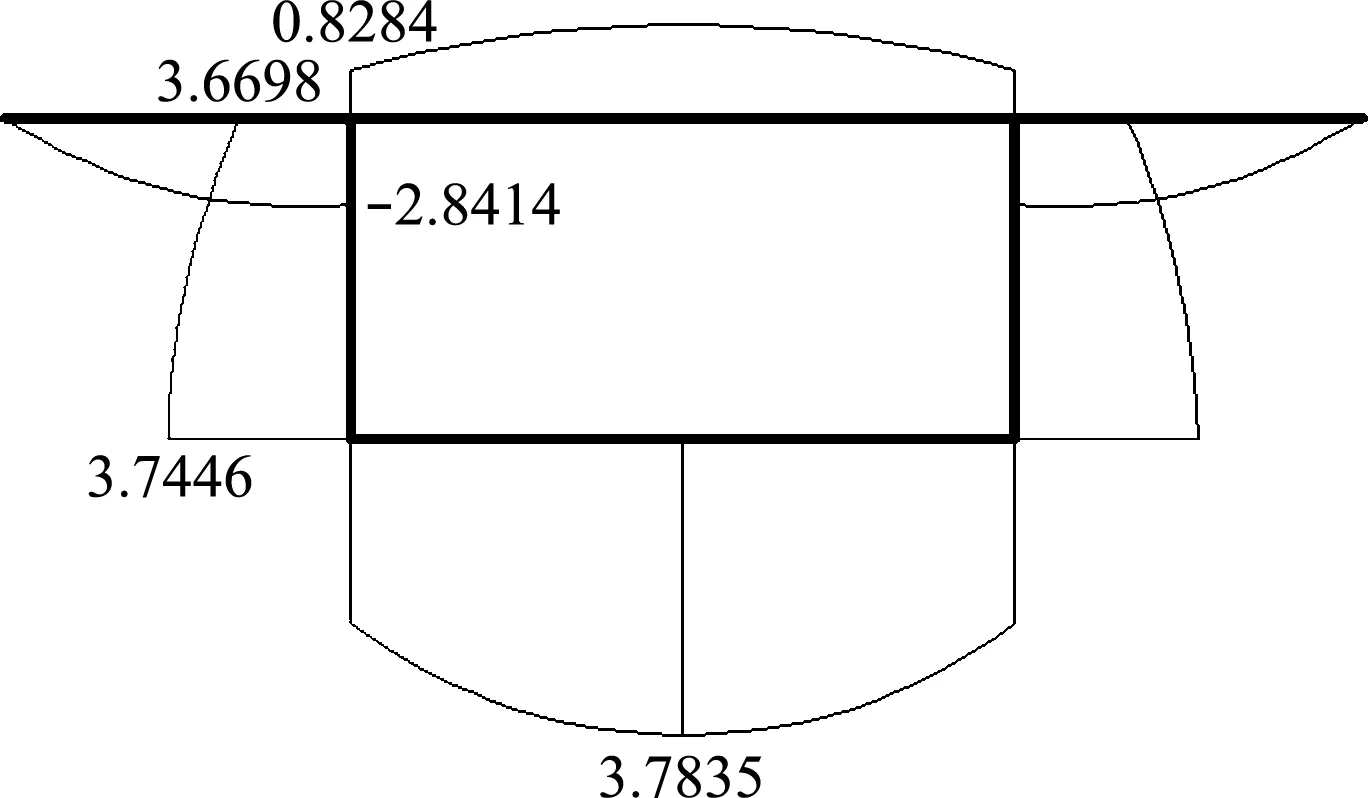

6.2 结果分析



6.3 对比分析



7 结 语

