珩磨加工中运动仿真分析与工艺实践

闵浩晨，宁会峰，2，龚 俊，2，师志鹏

（1.兰州理工大学机电工程学院，甘肃 兰州 730050；2.兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃 兰州 730050）

1 引言

珩磨是磨削加工的一种特殊形式，已成为发动机汽缸、工程机械液压缸与精密联轴器加工不可或缺的工艺技术。珩磨是缸孔的最终精密加工步骤，形成缸孔的结构形状、尺寸和表面精度，对缸孔的性能与寿命起到决定性作用。因此，研究缸孔珩磨的运动参数是十分重要的，在珩磨过程中，每条油石都均匀的固定在珩磨头上，珩磨头的运动直接影响缸孔珩磨的质量。所以这里着重对珩磨的运动、轨迹形成及加工过程进行分析，深入研究不同参数的选择对于珩磨加工质量的影响，从而选出最优的参数方案。

文献[1]建立了珩磨轨迹分布与珩磨去除量的转换关系，对珩磨轨迹进行了优化，提高了缸孔的形状精度；文献[2]使用MATLAB软件模拟和分析了发动机气缸镗孔过程中油石磨粒的轨迹，通过研究发现，磨粒分布存在缺陷，提出了改善气缸缸孔形状的几种措施；文献[3]以圆柱形珩磨头为研究对象，对珩磨头进行运动和动力学分析，探讨了珩磨头的设计与仿真；文献[4]建立了四种常用圆柱度误差评定方法的数学模型，并将收敛因子的粒子群优化算法应用于圆柱度误差的目标函数优化问题，比较了各种模型的计算精度；文献[5]以单体泵的柱塞孔为研究对象，构建了珩磨加工的有限元模型，对仿真分析做了比较、优选工艺参数。综合以上研究现状，珩磨的参数分析现在还处于摸索阶段，虽然理论研究和仿真分析做得比较充分，但是其并没有与实验相结合起来，能进行实验验证说明的研究现在还比较少。针对这一问题，首先对珩磨的三维轨迹进行重构，分析影响到珩磨轨迹的运动参数；其次选择参数建立加工方案，在仿真分析之后得出数据，对所得数据进行圆柱度误差评定。其中，圆柱度是评判缸孔加工质量的一个重要因素，如果圆柱度不在基本范围之内，缸孔形状会产生腰鼓形、马鞍形、锥形和桶形等不满足基本使用条件的废品，带来效率下降、寿命减短等问题。最后得到正确的圆柱度数据，对比缸孔之间质量水平不同，选择出最优的缸孔加工方案，并进行实验验证，实现珩磨加工运动参数对珩磨质量影响的综合性分析。

2 珩磨轨迹形成过程的分析

2.1 运动参数的选择

在珩磨的实际加工中，珩磨头旋转并往复运动，往复运动包括三个工作段：下行程、下端滞留和上行程。根据珩磨加工情况，选取实际加工的参数：在珩磨头上均匀分布着八条油石，珩磨头往复速度V、旋转速度n=230r/min、油石长度为l=60mm、缸孔高度L=150mm、两端越程量为l1=l2=20mm、下端停留时间t3=0.3s，油石上每隔15mm 取一磨粒点，这样沿油石的长度方向均匀的取4个点，可以直观的反映出磨粒轨迹的分布。

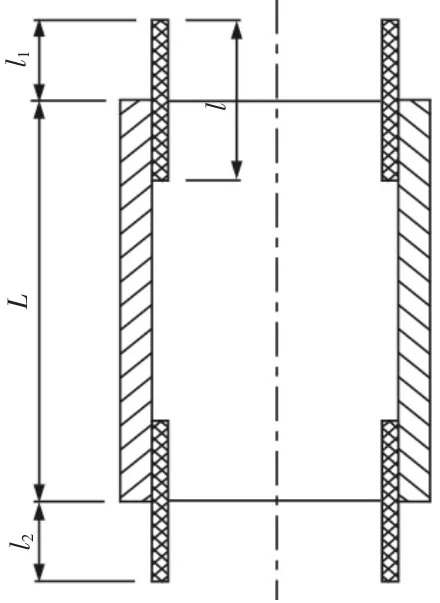
图1 珩磨加工示意图Fig.1 Honing Process Diagram

2.2 珩磨中油石三维轨迹的重构

当珩磨头的旋转速度、两端越程量和下端停留时间恒定，往复速度改变时，珩磨头的旋转相位角将相应地改变。珩磨头旋转的相位角角度，在改变往复速度的情况下，可以通过计算得到。珩磨头的行程距离Lx=L+l1+l2-l=130mm，油石下行程时间为t1=Lx/V；则油石上行程的时间为t2=t1=Lx/V，t=t1+t2+t3=（15.6/V）+0.3。珩磨头在一个周期内所转动的角度：θ=nt=n/60×（15.6/V+0.3）×360°=（15.6/V+0.3）×1380°。此时，在往复周期内选择合适旋转相位角，V=15.6×［（θ/1380-0.3）］。当V=15.6×［（9t-41.4）/138］，θ=πt/4（t为正整数），取t=28、26 时的运动轨迹图，当t=28 时，V=23.807m/min；t=36时，V=31.946m/min。根据以上参数进行计算，使用MATLAB 模拟出珩磨的三维轨迹图。

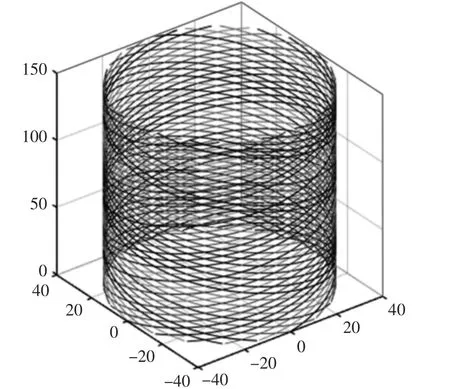
图2 往复速度为23.807m/min 时的三维轨迹Fig.2 3D Trajectory Reciprocat’s Speed at 23.807m/min

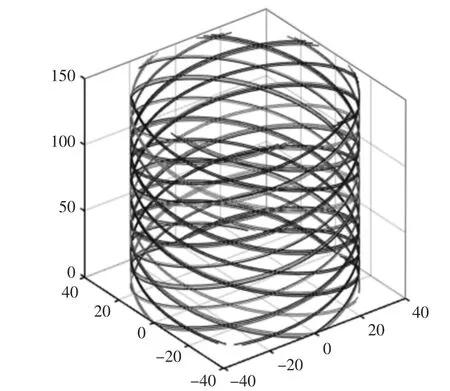
图3 往复速度为31.946 m/min 时的三维轨迹Fig.3 3D Trajectory Reciprocat’s Speed at 31.946m/min

在珩磨过程中，珩磨头的运动是旋转运动和上下运动的综合运动，因此油石的轨迹是交叉分布的，这样才形成了交叉网纹。而油石的旋转速度和往复速度决定了网纹的分布情况，在图2 与图3 中可以大致看出，在不同往复速度下，油石运动轨迹也产生了变化，珩磨头的往复速度影响到了缸孔珩磨的效果。

2.3 运动参数对珩磨轨迹的影响

现在将上述油石的三维分布轨迹转化成为二维图形，这样就能够更加直观的观察油石轨迹分布情况，如图4、图5 所示。对油石轨迹的分布差异直接进行对比。

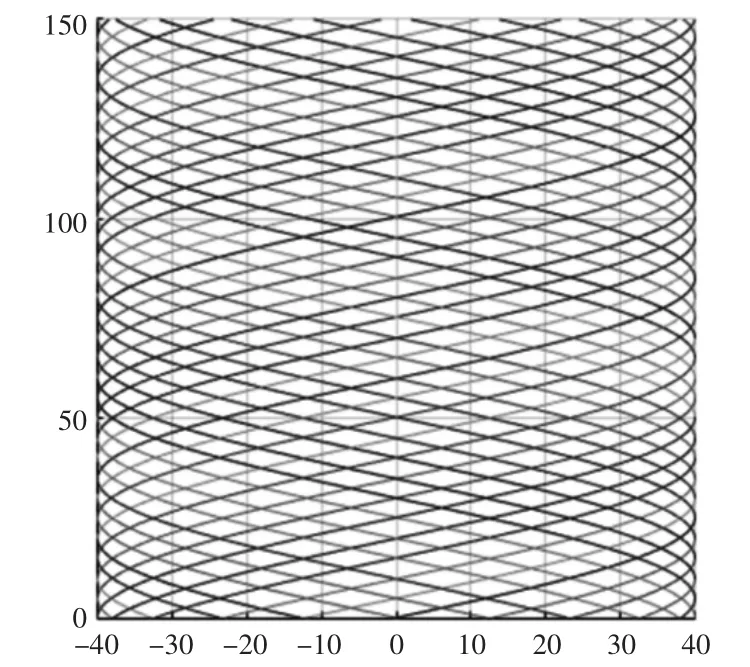
图4 往复速度为23.807m/min 时的二维轨迹Fig.4 2D Trajectory Reciprocat’s Speed at 23.807m/min

图5 往复速度为31.946m/min 时的二维轨迹Fig.5 2D Trajectory Reciprocat’s Speed at 31.946m/min

由上面的二维平面轨迹图分析可知，油石轨迹沿缸孔深度方向分布不均匀，而珩磨头的往复速度很大程度上影响到了磨粒的空间分布情况。图4 中的运动轨迹具有较小的重合度，网纹的分布比较相对均匀，所以缸孔内表面珩磨很充分，保证了缸孔的表面精度；而图5 中的油石运动轨迹重合度较高，这会导致缸孔的部分表面被重复加工，整体内表面加工不均匀，极大地影响到了缸孔的表面精度。通过上述表象分析，推断出了运动参数直接影响缸孔性能参数，但缸孔的性能参数影响值差异无法确定，针对存在的问题，通过对珩磨过程进行仿真分析，研究运动参数对于珩磨性能参数的影响。

3 珩磨加工的仿真分析

3.1 珩磨加工的仿真机理

珩磨加工过程中，在缸孔内壁发生微小的塑性应变，这种塑性应变等效交叉网纹的作用变量，这些变量的作用汇集在一起使得缸孔发生变形。珩磨仿真运算结束后，将会得到缸孔的应变云图，这时对缸体的变量数据进行采集、汇总，对集合起来的变量数据进行计算并分析出缸孔的圆柱度，对圆柱度误差进行评价。

3.2 建立三维模型

首先，建立珩磨头的三维模型，如图6 所示。建立模型时，要使用柱坐标系，将珩磨头结构尽量简化，在保证了基本结构的前提下，尽可能的提高运算速度。在仿真分析下，珩磨头与油石均不考虑其本身的磨损与变形，即珩磨头与油石是刚性实体，这样在一定程度上减少了多余运算量。

图6 珩磨头与缸孔的有限元模型Fig.6 Finite Element Model of Honing Head and Cylinder Hole

珩磨加工过程中，因为加工余量很小，所以仅需保留被加工材料的部分来制定缸孔的有限元模型，考虑到温度、应力和塑形变形的影响，采用Johnson-Cook 模型构建缸孔材料，实现磨削过程中切屑分离，在轴向方向细化了网格，能更加完整、精确的运算出真实的工况，最后，装配珩磨零件，获得完整的有限元模型。

3.3 模型参数赋予

仿真油石与缸孔材料的参数与Johnson-Cook 本构常数如下：

表1 缸孔材料参数与Johnson-Cook 本构常数Tab.1 Cylinder Hole Material Parameters and Johnson-Cook Constitutive Constants

珩磨在加工过程中有着加工速度快、精度高等特点，经过珩磨三维轨迹构成运动参数的分析：首先，珩磨头的往复速度是影响珩磨质量的一个重要因素；其次，珩磨过程的珩磨余量和下端滞留时间也会影响到缸孔材料的剥离程度。因此，针对这三个方面制定不同的工艺方案进行仿真，验证在哪一种方案下珩磨加工精度能达到最高，通过理论、仿真方法来验证假设是否成立，如表2 所示。

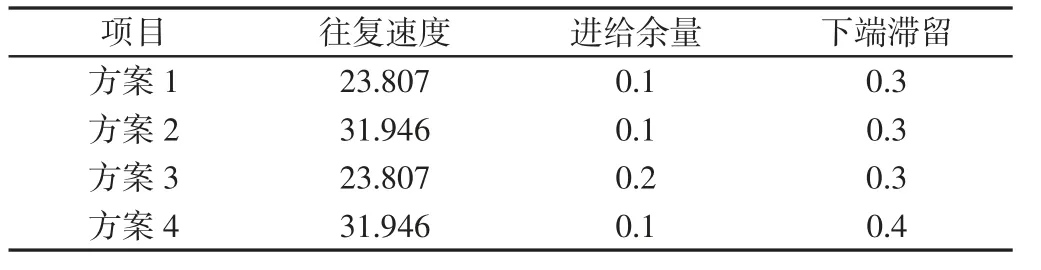
表2 制定的工艺方案Tab.2 The Processing Plan

在得到了仿真应变云图之后，对模拟运算加工后的缸孔坐标数据进行采集，如图7 所示。其中，方案1 的缸孔坐标数据，如表3 所示。

图7 仿真应变云图Fig.7 The Simulation of Strain Nephogram

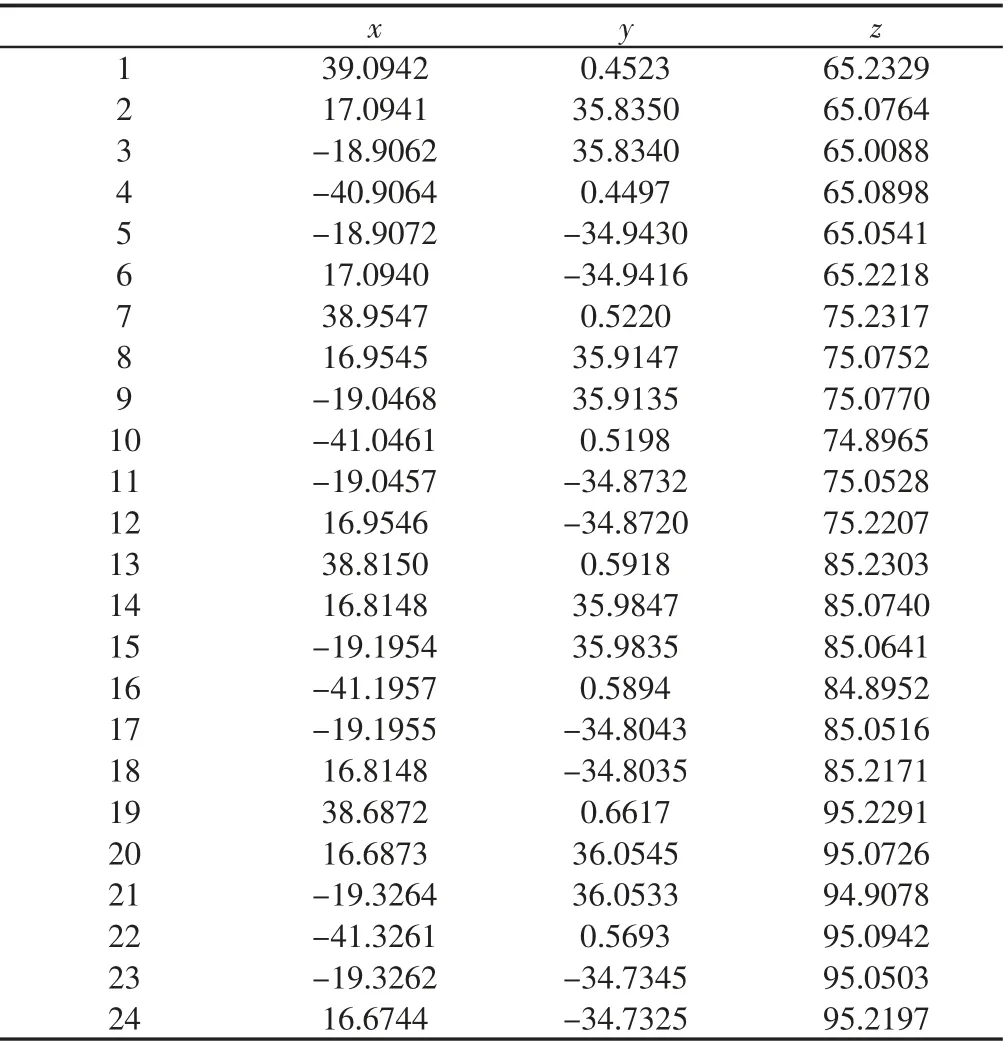
表3 缸孔变量数据Tab.3 Cylinder Hole Variable Data

4 仿真数据的后处理

4.1 圆柱度误差评价的数学建模

圆柱度误差指的是理想圆柱面与实际被测圆柱面之间的变动量，确定理想圆柱面的位置是误差评定的第一要素，理想圆柱面的选择应满足最小条件，即被测实际数据相对于理想数据的最大变动量为最小值。根据理想圆柱面的位置不同，分为最小区域法、最小二乘法、最小外接圆柱法和最大内接圆柱法，其中最小区域法是最为有效，计算结果最佳的结论[4]。

首先，建立空间直角坐标系，如图8 所示。设圆柱面的回转轴线为L，位置由参数a、b控制，方向由u、q控制，可推导出方程：

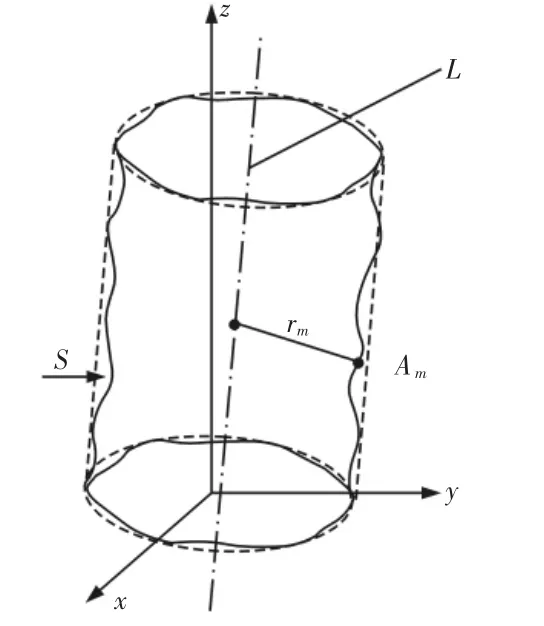
图8 被测圆柱面及理想轴线Fig.8 The Measured Cylinder Surface and Ideal Axis

最小区域法评价圆柱度误差的定义如下：被测对象由两个同轴的理想圆柱面包含其中，两个圆柱面的半径差为最小值时，它们之间包含的区域就是最小区域，半径差即为圆柱度误差。根据最小区域法定义，得出圆柱度误差目标优化函数为：

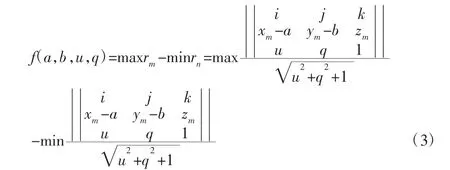
4.2 圆柱度误差的数学运算

而将方案一至四的缸孔坐标数据均采集并逐步迭代运算，得到的结果，如表4 所示。

表4 仿真计算的圆柱度Tab.4 The Simulation Calculation of Cylindricity

可以看出，方案1 与2 的进给余量与下端滞留时间相同、往复速度不同的情况下，所得到圆柱度的数值明显相差，表明珩磨过程的往复速度对缸孔精度有一定的影响。方案1 与3 的往复速度与下端滞留时间相同、进给余量不同的情况下所得到圆柱度的数值最小，进给余量对于缸孔精度的影响并不明显。方案2 与4的往复速度与进给余量相同、下端滞留时间不同的情况下，发现下端滞留时间对于缸孔精度的影响不大。

5 珩磨的加工实验

5.1 珩磨的实验设备

前面进行了珩磨三维轨迹、加工模拟、仿真分析，虽然计算已经得出满足要求的圆柱度数据，但是没有经过试验验证，理论分析依然具有一定的局限性。我们将计算参数运用于实践加工，利用仿真数据开展实验。前面建立的珩磨磨削加工模型是从三维轨迹的成型机理出发，依据理想工况做出假设而得到的，需要试验验证其是否对实际加工具有指导意义。

实验设备为银川大河2MK2210 型数控珩磨机床，机床配备的珩磨头可加工的工件为内孔直径为Φ80mm～Φ100mm 的工件。机床自身量仪可以实现在线测量并可以实现自动加工。

图9 银川大河2MK2210 型数控珩磨机床Fig.9 Yinchuandahe’s 2MK2210 NC Honing Machine Tools

为了验证珩磨加工测量精度，能够快速的测量出精度数据，专门配备了PULCOMV4 量仪。PULCOM V4 电动测量仪连接机床系统进行有效测量，实现对工件的在线实时测量和加工后的手动测量。该气动量仪最小分辨尺寸为0.1μm，数值显示可以根据倍率变换进行自动调整，可显示最大范围为（±999.9）μm，且表头可根据量程的切换显示（±10～±50）μm、（±100～±500）μm 的测量范围。

5.2 加工实验结果分析

图10 实际加工图Fig.10 The Actual Processing Figure

珩磨加工后的实验工件，从左往右分别是按方案一至方案四顺序排列，在工件内部可以看到清晰的加工珩磨网纹，每个加工工件内表面光洁度均有不同，表面质量明显存在差异，并存不同规律的珩磨网纹，如图10 所示。通过观察发现方案1、3 的珩磨网纹平整、连接性平滑，方案2、4 的珩磨网纹与方案1、3 有明显的差距、连接性也有所降低，这表明运动参数的选择直接影响珩磨的精度。使用珩磨机床上的气动测量仪（PULCOM V4 量仪）对工件进行测量，测得的结果，如表5 所示。

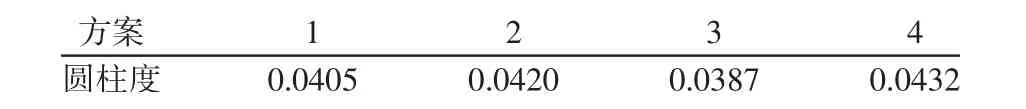
表5 实验加工的圆柱度Tab.5 The Experiment Process of Cylindricity

将所有方案结果统计绘制出圆柱度对比图，如图11 所示。利用仿真数据与实验结果进行整理和对比分析，实验测量精度与仿真计算数据非常接近，两条折线的相似度也非常高，通过使用仿真参数加工缸孔，可以有效的控制缸孔的圆柱度精度，获得较好的珩磨效果。

图11 仿真计算与实验加工的圆柱度对比Fig.11 The Simulation Calculation and Experimental Processing’s Cylindricity of Contrast

在理论和实验的结合过程中，突出解决了三个关键问题：

（1）通过珩磨运动参数构建了珩磨加工三维轨迹，其中珩磨头的运动参数是影响缸孔轨迹的主要因素，重点分析在不同参数下形成的不同的运动轨迹，从而得到了珩磨几何轨迹、疏密分布程度和缸孔圆柱度之间的关系，初步建立仿真分析方法。（2）珩磨仿真运用实际加工中，现在在国内仍处于空白阶段，相关理论研究内容较少，这里通过运动参数的选择、三维轨迹的重构、珩磨加工的仿真创建模型、圆柱度误差评价的数学建模、设置接触以及设立边界条件等一系列理论流程实施后，构建了珩磨加工的仿真系统，能够模拟珩磨加工并运算出在理想条件下缸孔加工的应变云图。（3）圆柱度误差的评价采用了最小区域法，得到了仿真应变云图与形变云图，通过采集仿真缸孔数据计算出圆柱度，在与实验测得的圆柱度进行对比，验证运动参数对于加工质量产生影响。这种参数优化的思路与实验过程相结合的方法，将为今后的制造和设计提供有力的理论指导。

6 结论

围绕珩磨过程中运动参数选取，运用三维轨迹和有限元模型分析，在不同参数下对缸孔圆柱度影响进行分析，得到了珩磨过程中往复速度对缸孔圆柱度的影响效果；通过理论仿真结果与实验研究数据对比和分析，证明运用优选方法可以准确确定珩磨过程中运动参数，得到最佳的珩磨缸孔圆柱度，达到保证加工精度的目的。