改进扰动观测优化轮毂电机无位置控制

赵九九，闫 洁

（1.长春汽车工业高等专科学校电气工程学院，吉林 长春 130013；2.吉林大学，吉林 长春 130013）

1 引言

全电化车体已经成为未来发展趋势，通过永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）将驱动力直接传递到装甲履带，相比于传统机械传动及燃油造成的尾气污染，具有更好的控制性能，且机体积小、强度高，适于在车体轮毂整体安装。但传统PMSM 设备的位置传感器故障频发，且转矩脉动大、抖振明显、抗扰动能力差[1]，因此，为提高PMSM 电机的控制性能，研究基于无位置传感器的PMSM 电机预测控制方法具有重要作用。

为此，文献[2]通过三种算法合并滤波器与惯性环节，提出SMC 和MTPA 的混合正交模型，其主要抑制电机的三相电流谐波，对启动电流及其谐波率有较好的改进，但算法依赖于磁链值，且在转速突变时引入较大误差；文献[3]对磁链脉动进行基于PLL 的改进，提出双滑模控制算法，但算法的位置补偿精度较低，超调误差较大；由于PMSM 转子在低速时其反电动势较小，在零速或低速时，上述算法不再适用，为此，文献[4]将传统滑模符号函数修正为分段指数有效削弱了滑模抖振，提高其对电流的响应速度，但算法仍未解决超调问题，且自适应性能不足；文献[5]通过低通滤波器改进电机控制算法的滑模观测器，以实时快速跟踪电机转子位置，但其固定的截止频率对高频分量的自适应能力较差；文献[6]通过流频比优化零/低速控制和开环启动带载能力，采用融合过渡处理速率切换，有效消除零漂问题；文献[7]提出高频注入与模型参考相融合的全速区复合电机无位置控制策略，提高了预测控制性能；文献[8]采用改进的模型参考自适应算法以提高控制策略对参数的辨识能力，以增强对电机参数时变的适应性。

PMSM 转子的位置观测通常由反电动势法和磁路凸极法两大类算法实现，前者在零/低速时因电动势激励不足而无法观测位置，而后者的额外激励注入会干扰PMSM 的基本控制，两种方法组合存在高效切换和速区合理选择问题[7]。为此，提出改进扰动观测器的反电动势[10]电机无位置传感器控制算法，算法将电流反电动势作为观测干扰量进行建模，以实现扰动准确估计，进而通过反正切变换实现转子位置的精确估计与误差补偿，仿真实验验证了算法的有效性。

2 参数自适应控制算法

实际使用过程中，经典扰动观测器控制依赖于模型参数的精确性，导致与电机的实际运行规模不匹配。为此，提出参数自适应设置的改进扰动观测器，以缓解经典算法对模型参数的敏感性。

2.1 改进电机扰动观测模型

式中：ud、uq—定子在d、q轴电压；id、iq—对应电流；Ld、Lq—对应静态电感；ld、lq—对应动态电感；R—定子电阻；ψf、ωe—转子磁链和电角速度。根据自抗扰思想[11]，设中间变量z=d^-Lx，则改进扰动观测模型：

可以看出，改进模型同时避免了额外信号注入，从而减少外界信号干扰对模型控制性能的影响。

2.2 位置观测估计

将式（6）改进扰动观测器代入电机电流状态方程中，模型中振动量为反电动势e=（ed，eq）T，可得[10]：

其中，补偿角θc=arctan（Ls pωr/l）可以根据电机转子的转速对其位置进行补偿。根据以上分析，基于改进扰动观测器的位置观测器估计过程，如图1 所示。

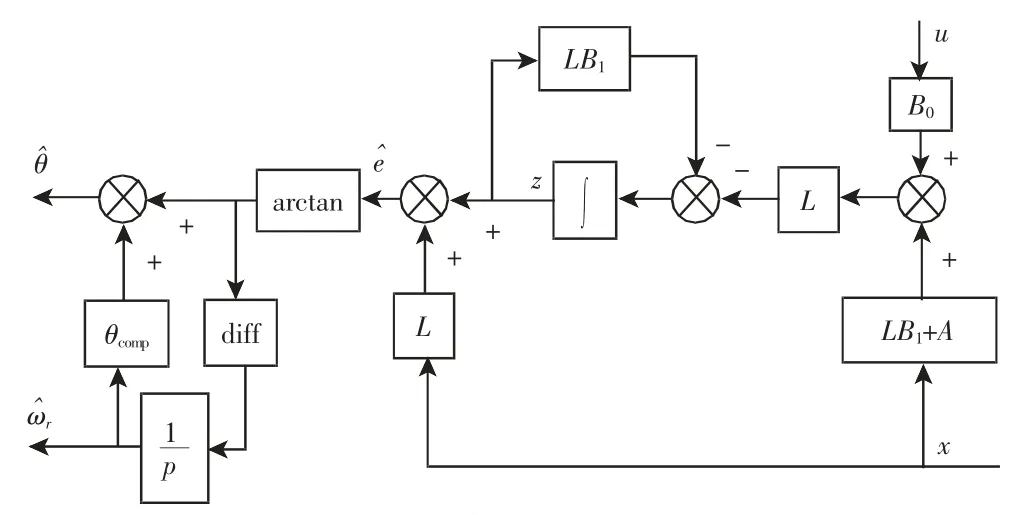
图1 无位置传感电机的位置估计Fig.1 Position Estimation of Position Sensorless Motor

2.3 初始磁极辨识

位置观测器不能有效区分南北磁极，较大的初始误差会导致收敛错误，因而需要辨识初始磁极。设位置观测速度高于磁极辨识收敛速度，即辨识在位置误差收敛后，则用于无位置传感器电机的初始磁极辨识计算式为[9]：

此时，当增益l＜0 时，有＜0，其满足稳定性要求，说明当前位置观测器收敛，根据观测可以进行初始磁极辨识，需要说明的时，初始磁极辨识只在算法开始时进行，且仅需要完成一次即可。

基于改进扰动观测器模型，无位置传感器电机的预测控制策略的系统框图，如图1 所示。

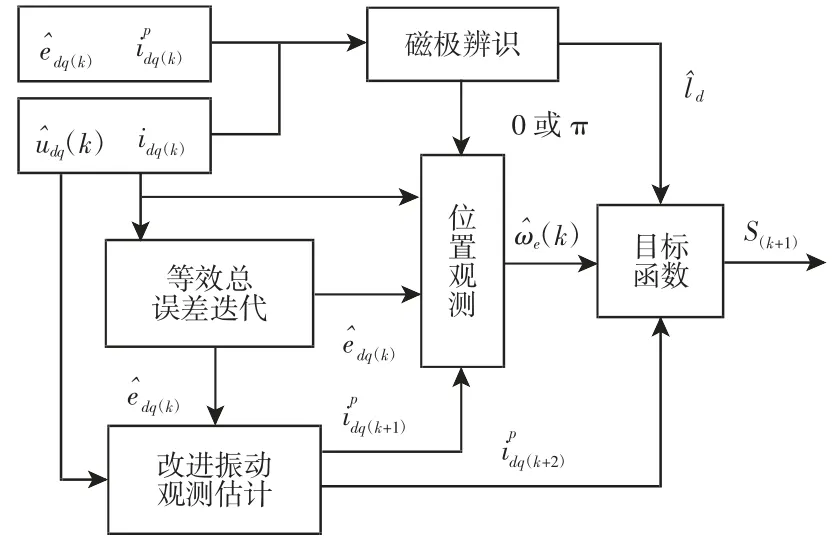
图2 改进算法控制框图Fig.2 Block Diagram of the Improved

3 仿真实验与分析

以某轮毂内置式PMSM 作为研究对象，如图3 所示。被控pmsm 与负载电机相连，在Matlab 2016a 中搭建实验环境，仿真搭建电机与图3 电机原理相同，电机参数对控制器不开放。以电机的光电编码器获得的转子位置作为实际位置，用于控制结果比较。

图3 实验用内置式PMSMFig.3 Experimental Built-in PMSM

为分析位置估计补偿算法有有效性，将转子的转速以20%额定转矩启动并逐渐增加转速，实验时间为1.4s，在1.2s 时转速达到预设值并稳定运行，观测器增益l取值分别为－5、－10 和－20，实验过程转子位置误差哪图4 所示，可以看出，随转速增加转子的位置误差也逐渐增大，并在转速稳定时，达到稳态误差，且l值取值越大稳态误差越大。相同实验条件下，增加位置补偿算法后的转子位置误差，如图5 所示。实验过程中将转速与位置进行反馈以实现无位置传感器预测控制，可以看出，经过位置估计补偿算法的补偿后，转位置误差变得非常小，甚至忽略不计，从而验证算法的有效性。但根据图4 结果，观测器增益l就尽量取较小值，以减少补偿算法负担，增加算法的鲁棒性。

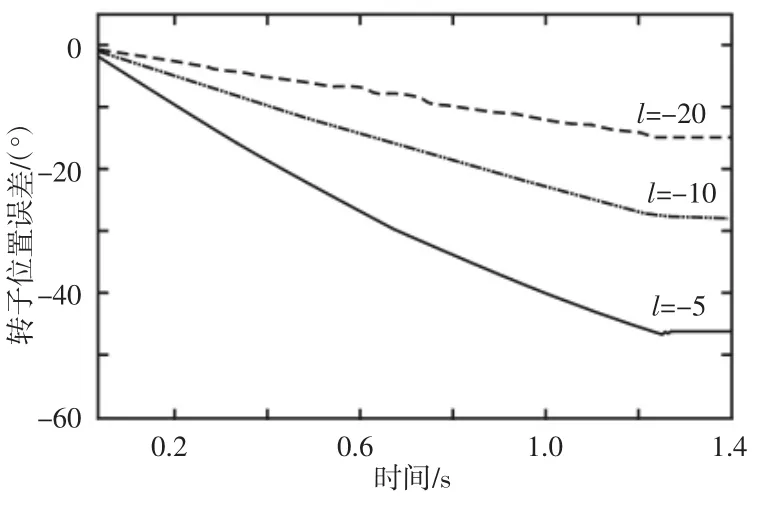
图4 观测器增效对位置误差影响Fig.4 The Effect of Observer Efficiency on Position Error

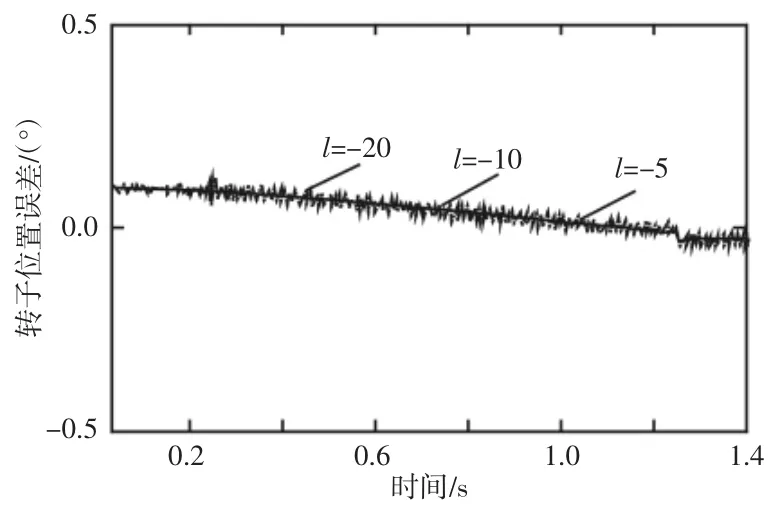
图5 位置补偿器对位置误差改进Fig.5 Improvement of Position Error by Position Compensator

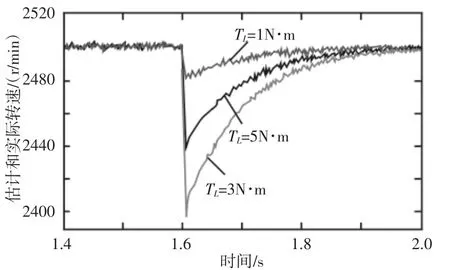
图6 负载变化对算法控制性能的影响Fig.6 Impact of Load Changes on Algorithm Control Performance

对算法进行负载变化适应性实验，其实验结果，如图6 所示。图中，在1.6s 时刻增加TL=｛2，5，10｝N·m 的负载，从图中实验结果可以看出，负载转矩增加时，转子的转速会有较大的幅值变化，但转速估计算法仍可以准确跟踪，由此可知，文中基于改进扰动观测器的无位置传感器预测控制具有较强的鲁棒性。

4 结论

针对传统扰动观测造成的噪声放大问题，提出基于改进扰动观测器的无位置传感器控制算法，算法将电流反电动势作为观测干扰量进行建模，并通过反正切估计转子的精确位置，同时基于转子速度进行位置误差补偿，实现电机的鲁棒控制，仿真实验表明，改进算法在在电机不同工况和负载下能准确估计转子位置，具有较好的适应能力和位置跟踪补偿能力，验证了算法的有效性。