长江叙渝段航道最大开发尺度研究
李文杰,王 皓,龙 浩,杨胜发,肖 毅,杨 威
(1. 重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074)
长江三峡工程蓄水后,大坝至重庆涪陵常年回水区已建设成高等级航道,通航条件明显改善[1],基本满足通航船舶大型化的航道尺度需求。重庆至宜宾段航道经泸渝段航道建设工程后技术等级为Ⅲ级,维护水深仅为2.9 m,而长江上游航运需求发展导致船舶大型化趋势明显,低水位时期航道尺度不足的问题越发凸显[2]。基于自然条件评估航道最大开发尺度是合理利用航道资源的先决条件,也是航道开发建设的基础,我国学者曾总结国内航道整治实践,建立航道最大可开发尺度与流量和比降关系的经验式[3],但该式缺乏理论支撑,相关学者又提出了稳定航深法和等级流量法[4]。等级流量法是将航道开发成各标准航道等级理论上所需的通航流量,与天然情况下的设计最低通航流量比较,进而确定航道最大开发尺度。稳定航深法是假定整治后枯水断面与优良河段断面形态相近,并基于优良河段特征流量下河相关系,推求整治后航道可能达到的最大航道深度。目前上述方法已在西江、岷江等流域的航道建设规划中得到初步应用[5-8],但实际操作过程较为复杂。
本文拟根据长江宜宾至重庆河段的实测水文地形资料,基于河相关系对稳定航深法进行优化改进,简化稳定航深值的计算过程,针对长江上游航道尺度亟待提升的宜宾至重庆河段,运用改进稳定航深法计算该河段不同航宽标准下的最大航深值,评估其航道的最大可开发尺度,以期为该河段后续的航道建设规划提供支撑。
1 数据来源及研究方法
1.1 数据来源
长江上游宜宾(上游航道里程1 044 km)至重庆江津(上游航道里程726 km)河段地形数据使用2015 年实测地形数据,由于长江上游属于典型山区河流,山区河流河床以岩质河床和卵石河床为主,其河床形态相对稳定[9],认为选择2015 年地形具有代表性。以该河段最低设计通航流量2 230 m3/s,流量12 100 m3/s 以及流量20 291 m3/s 为三种特征流量,最低设计通航流量有35 个设计水位点,其余两种特征流量下水位来源于2016 年实测的30 个水尺点数据,三级流量下的水位见图1,用于研究不同流量下河相关系参数的变化规律。朱沱站(上游航道里程806 km)水位流量关系见图2,用于验证河相关系变化规律。

图 1 宜宾至重庆三级流量下沿程水位Fig. 1 The water level from Yibin to Chongqing for three flow discharges
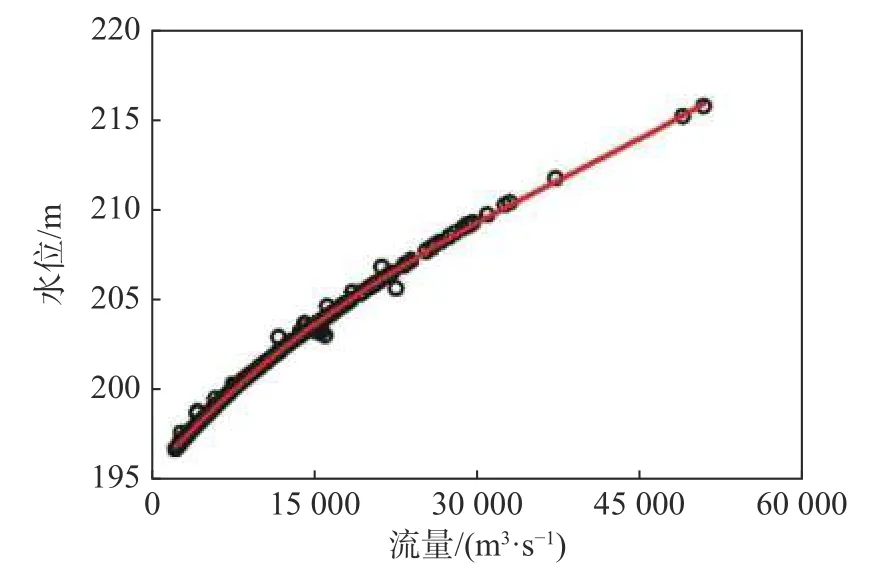
图 2 朱沱站水位流量关系Fig. 2 The relationship between water level and flow discharge at the Zhutuo station
根据设计最低通航水位求得宜宾至江津河段枯水平均比降为0.253‰。张有林等[10]在建立向家坝至朱沱的计算模型时,模拟糙率范围为0.022~0.048,平均糙率为0.035;朱代臣等[6]认为长江干线泸渝段河床糙率取值范围为0.030~0.045,平均糙率为0.038;何大伟等[11]认为川江河段糙率取值为0.025。本文综合上述资料,为计算方便,取叙渝段平均河床糙率为0.033。
1.2 稳定航深法原理
稳定航深法需先确定天然河道的优良河段,优良河段可被认为是航道整治工程参考的样板。一般认为在河流演变过程中河道形态比较顺直,且经过历年冲淤后河床变形不显著,对航行没有障碍的河段属于优良河段[4]。优良河段的河相关系[12-14]意在描述天然状态下河流通过整治后可达到的最稳定的河床断面形态。假定航道在完成整治后的河道断面与优良河段的断面形态相似,据此建立某一特征流量(一般为设计最低通航流量)下的河相关系,见下式[15]。

式中:B为水面宽度;H为河道断面平均水深;α、β为河相关系参数。
假定河段经过航道整治后流量Q、糙率n及平均水面比降J保持不变,根据水流连续方程和曼宁公式联解得:

式(1)和式(2)联立得到某断面经过航道整治后可达到的稳定平均水深如下:

对于任何一个河道断面来说,都存在断面平均水深H与航道水深h的函数关系,其关系可写成H=ηh形式,其中η为水深修正系数,代表断面平均水深与航道边缘水深的比值,由此可通过水深修正系数将平均水深转化为稳定的航道水深。目前,求解水深修正系数时,首先需要给定航宽,然后量取该航宽下的航道边缘水深,最后点绘断面平均水深和航道边缘水深的相关关系,由此推求水深修正系数。
综上,采用稳定航深估算法估算某河段的航道可开发尺度时,首先需要根据特定流量下断面形状数据率定沿程的河相关系参数α和β,计算航道整治断面可达到的稳定平均水深;然后确定某个设计航宽标准,量测该航宽下的航道边缘水深,推求水深修正系数η,进而将稳定平均水深转化为稳定航道水深,根据航宽和航深可判定河道可开发的航道尺度。
1.3 稳定航深法的改进思路
1.3.1 河相关系改进 长江上游修建有梯级水库群,考虑到水库调度等因素的影响,虽然相关管理部门颁布了设计通航流量,但该流量仍有调整的空间。当最低设计通航流量发生改变时,平均水深和河面宽度会随之改变,该方法所需参数数α和β则需重新率定得到。因此,为提升稳定航深法的计算简易性,应考虑寻求建立河相关系参数与流量的直接联系。拟先统计分析不同流量下叙渝段河相关系,然后提出河相关系参数随流量的变化规律,进而直接求得给定流量下稳定航深法所需的河相关系参数。
1.3.2 水深修正系数改进 传统稳定航深法中设计航宽发生改变时,需重复测量边缘航道水深,进而率定出设计航宽改变后的水深修正系数,过程较为繁琐,拟寻求水深修正系数随设计航宽的变化规律。图3 是天然河道的单式断面形态示意图,其中H为断面平均水深,h为航道深度,Hm为断面最大水深,B为水面宽度,b为航道宽度。
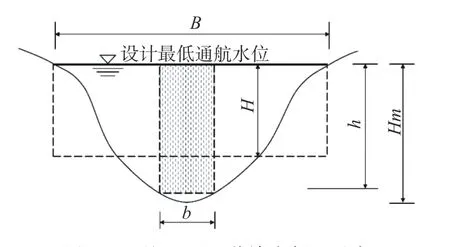
图 3 天然山区河道单式断面示意Fig. 3 Single-section profile of a natural mountain river
假定位于单式断面航道下端的区域形状相似于整个断面形状,根据几何相似原理存在如下关系:

提出河道断面形状系数k的概念,即断面最大水深与断面平均水深之比。将Hm=kH代入式(4),可得水深修正系数η:

若河道断面为完全“V”字形时,河道断面形状系数等于确定值2,但实际河道条件复杂,可能存在分汊河段或复式断面,k值随断面形状波动较大,拟先统计不同流量下断面形状系数的变化规律,然后直接利用流量和设计航宽计算水深修正系数。
优化后的稳定航深法计算某河段航深时,首先通过流量确定河相关系参数进而计算稳定平均水深,然后通过设计流量和航宽确定水深修正系数进而将稳定平均水深转化为稳定航道水深。
2 稳定航深法改进结果
2.1 不同流量下的河相关系
根据宜宾至重庆河段三级流量下水位数据,考虑比降线性内插得到739 个优良河段断面的水位数据,并以优良河段断面宽深数据在式(1)的基础上进行曲线拟合,拟合结果详见图4。
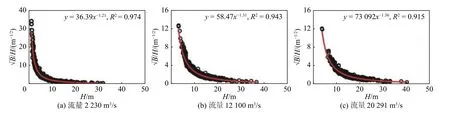
图 4 宜宾至重庆河段沿程断面河相关系Fig. 4 River hydraulic geometry relation of the Yibin-Chongqing reach
通过对宜宾至重庆段三级流量下河相关系的分析可知,河相关系系数α随流量的增加而增大,而河相关系指数β随流量的增加而减小(图5)。通过图5 可知,在确定了特定河段的理论河相关系系数变化规律后,只要给出流量,即可确定参数,简化了繁琐的河相关系参数率定过程。并基于图5 得到的叙渝段河相关系参数与流量的关系,以朱沱站3 400~20 800 m3/s 流量下的7 组断面参数验证河相关系随流量变化的合理性(图6)。

图 5 三级流量下宜宾至重庆段河相关系参数变化Fig. 5 River hydraulic geometry parameters against flowdischarge from the Yibin-Chongqing reach
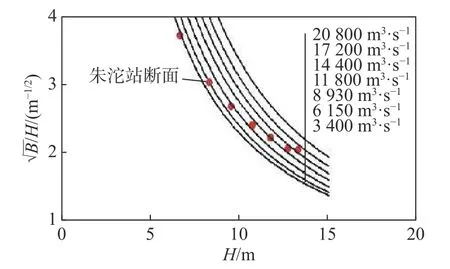
图 6 朱沱站断面多级流量下的河相关系验证Fig. 6 Validation of hydraulic geometry equations using the data of Zhutuo station
由图6 可知,提出的叙渝段河相关系参数与流量的关系,在10 000 m3/s 下与朱沱站实际断面的吻合程度较高。由于长河段水位资料有限,只在三级流量下分析了河相关系参数与流量的关系,因此拟合的河相关系式在洪水期的验证误差相对较大。
2.2 不同航宽下的水深修正系数
为了分析河道断面要素随流量的变化,将叙渝段三级流量下优良河段各个断面自然河宽B和断面形状系数k做移动平均,结果见图7。
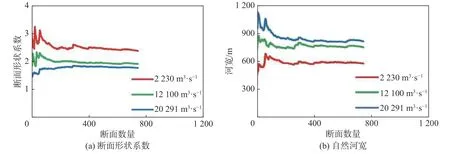
图 7 宜宾至重庆段三级流量下自然河宽、断面形状系数Fig. 7 River width and cross-sectional shape coefficient under different flow discharges of the Yibin-Chongqing reach
可知断面数量达到一定值后,平均河宽和平均断面形状系数趋于稳定。其中最低设计通航流量2 230 m3/s 时,叙渝段稳定自然河宽为577.47 m,稳定断面形状系数为2.38;流量为12 100 m3/s 时,叙渝段稳定自然河宽为749.73 m,稳定断面形状系数为1.91;流量为20 291 m3/s 时,叙渝段稳定自然河宽为812.93 m,稳定断面形状系数为1.77。基于上述数据,分析得叙渝段断面形状系数和自然河宽随流量的变化关系见图8。基于断面形状系数和稳定河宽,拟定设计航宽为50~200 m,可根据式(5)计算叙渝段三级流量下水深修正系数随设计航宽的变化趋势(图9)。
由图9 可知,水深修正系数随设计航宽的增加而线性增加,且在同一设计航道宽度下,流量越大,水深修正系数也会增大。
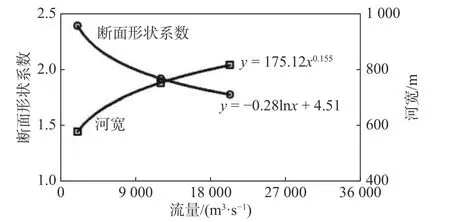
图 8 三级流量下断面形状系数及河宽随流量的变化Fig. 8 Cross-sectional shape coefficient and river width against the flow discharge
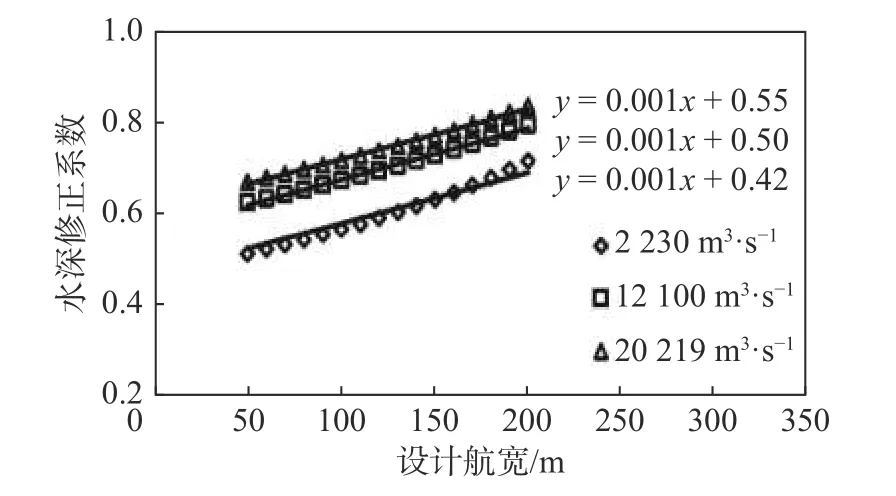
图 9 宜宾至重庆段水深修正系数与设计航宽的关系Fig. 9 Relationship between the depth correction coefficient and the waterway width of the Yibin-Chongqing reach
3 叙渝段航道最大开发尺度估算
叙渝段设计最低通航流量2 230 m3/s 是在向家坝水电站设计下泄流量1 200 m3/s 的基础上加上岷江流量入汇等计算得到,而向家坝水电站实际运行以来最低下泄流量稳定在1 600 m3/s 以上。虽然设计通航流量不考虑此流量的增加,本文初步分析设计通航流量增加400 m3/s 时稳定航深值的变化情况,即分析流量为2 230 m3/s 和2 630 m3/s 两种工况。在改进稳定航深法的公式基础上,结合沿程优良河段河相关系,计算叙渝段航道整治后在两种流量下开发成各航道等级(设定航道整治宽度b=60~150 m)可能达到的最大稳定航深,后续将理论稳定航深值与标准内河航道等级下不同设计航宽的航深对比,即可判定河道可开发航道尺度,计算结果见表1。
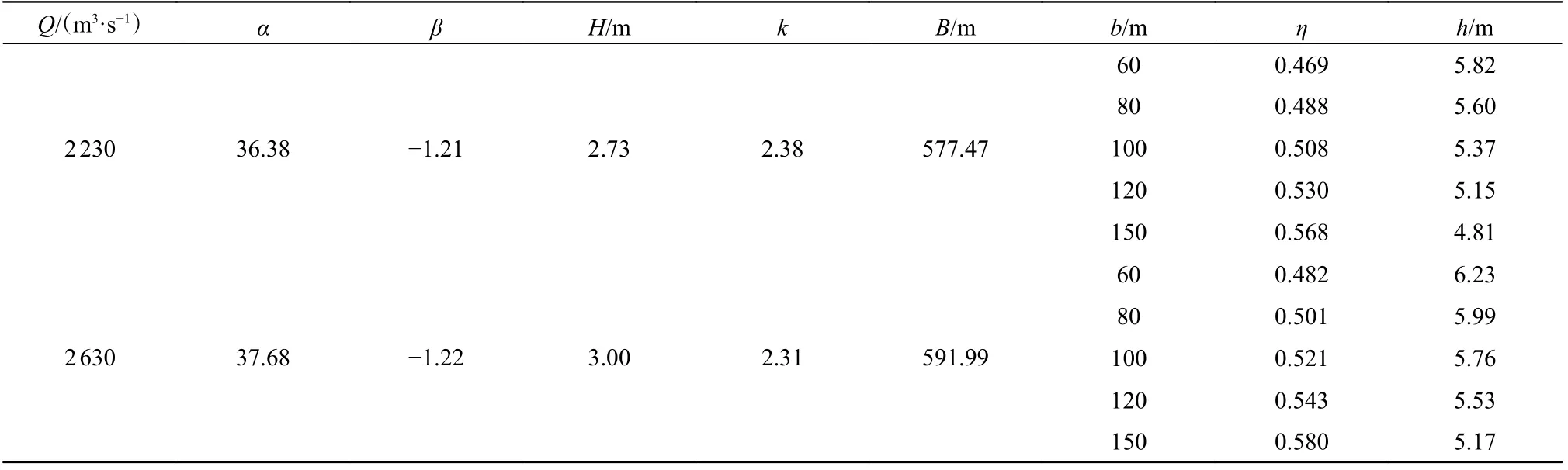
表 1 宜宾至重庆河段稳定航深估算Tab. 1 Estimation of the stable waterway depth of the Yibin-Chongqing reach
由表1 可知,通航流量为2 230 m3/s 时,拟定设计航宽从60 m 增加至150 m,稳定航深值由5.82 m减少至4.81 m。而流量为2 630 m3/s 时,拟定设计航宽从60 m 增加至150 m,稳定航深值由6.23 m 减少至5.17 m。设计通航流量增加400 m3/s,任意设计航宽标准下的稳定航深值可平均增加约0.39 m,因此,向家坝设计下泄流量若批复增加,有利于叙渝段航道尺度的提升。长江上游宜宾至重庆段正在规划提升航道等级达到Ⅱ级航道3.5 m×100 m 的设计标准,并且随着上游航运的发展,航运需求逐步提高,航道尺度有可能需要达到I 级航道4.5 m×150 m 的设计标准,从自然条件下的航道最大开发尺度来看均是可行的。
4 结 语
长江上游枯水期航道尺度不足问题日渐严重,而航道建设开发需要在考虑自然条件的基础上估算最大开发尺度。本文基于河相关系理论,针对叙渝段实际航道情况,在传统稳定航深法的基础上,对其存在的部分繁琐工作进行相应改进,计算了不同设计航宽标准下的稳定航深值,提出了宜宾至重庆段河相关系参数随流量的变化关系,当特征流量发生变化时,无需重新率定河相关系,可直接求得相关参数。提出河道断面形状系数,建立了水深修正系数与设计航道宽度的关系式,可直接计算设计航宽变化下的水深修正系数。
基于改进后的稳定航深法对宜宾至重庆段航道开发尺度进行估算,结果表明:叙渝河段通过航道整治可达到Ⅱ级航道3.5 m×100 m 及Ⅰ级航道4.5 m×150 m 的标准,可为长江上游河段的航道建设规划提供支撑。
本文虽然通过改进后的稳定航深法计算得到稳定航深值,但在计算的过程中,一些重要参数并没有根据实际情况分河段取值,如河流比降和糙率等,所以其计算结果对于较长河段来说往往只具有参考性,研究结果适用于类似河道、河岸组成相对接近的山区河流特定河段。由于资料有限的原因,只在三级流量条件下研究了叙渝段河相关系参数和断面形状系数的变化规律,后续应测量分析更多级流量下的变化规律以及糙率的取值,增强本研究的适用性。

