TIGGE 多模式降水预报产品检验与集成研究

舒章康 ，汪 琳 ，金君良 ，王国庆 ，曹民雄

(1. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；2. 长江保护与绿色发展研究院，江苏 南京 210098；3. 水利部应对气候变化研究中心，江苏 南京 210029)

数值天气预报是根据天气演变过程的流体力学和热力学的方程组，在一定初值和边界条件下，求解未来一定时期内大气运动状态和天气现象的预报方法。由于不同模式的初始场、初始扰动生成、参数化方案、模式框架等各不相同，因而其预报效果也具有明显的时空差异[1-2]。利用合理的检验方法评定数值天气预报在时间和空间上的适用性对资源合理配置与决策（管理的）、理解并改进预报系统（科学的）和预防与减轻自然灾害（经济的）等具有重要意义[3]。同时，针对预报误差采取一定的集成或修正方案，不仅可以为数值预报发展和进步提供参考，还可以为陆面水文过程模拟预测提供可靠精度的数据输入[4-5]。数值预报发展至今，其检验方法也在不断进步，最古老的方法是通过目视进行对比分析，目前多采用命中率（POD）、预报偏差（BS）、空报率（FAR）及漏报率（PO）等指标从时间和空间等角度进行综合评价[6-9]。

在降水集成或订正方面，诸多研究人员采取加权平均、多元回归或概率匹配等方法对产品进行再处理，以提高产品预报精度。如卞赟等[10]采用集合平均、多模式消除偏差集合平均、加权消除偏差集成等方法对TIGGE 资料中的多种模式产品进行了集成预报，结果表明集成预报相对于单模式预报的效果更优。刘汉武等[11]针对巢湖的多模式降雨预报产品，采用预报效果加权平均法开展了集成预报研究，结果表明集成预报相比单模式预报误差明显降低，预报准确率有所提高，对不同时效和量级降雨的预报效果相对更加稳定。荣艳敏等[12]则采用概率匹配平均法针对山东省典型的强降水过程进行了再预报，结果表明该方法相对于集合平均，对大雨以上量级降雨的预报效果有明显改善，较单模式的确定性预报也有一定的提高。

随着探测信息的日趋丰富和预报方法的增加，一方面使天气气候预测与诊断中的信息量成倍增长[13]，可以参考的资料信息内容更加丰富、种类更加齐全；另一方面也不可避免地产生对同一预报对象有多个预报结果不同甚至截然相反的结论，使综合集成的难度加大。近年来，随着预报产品的日趋丰富和综合集成预报服务需要的增强，全国各地的台站都相继开展了预报客观集成方法和技术的研究。尽管迄今为止国内外尚没有一种成熟而有效的集成技术，但围绕集成的基本原理、思路和目的，一些既有理论基础，同时又有较好集成预报效果的集成预报方法逐渐形成。如选择最优法、回归集成预报法、加权平均法、相对权重法、交叉相关法、条件频率法等，其基本思路都是将各种预报结果做统计平均，从而进一步改善预报过程中的薄弱环节，提高预报服务水平[14-15]。

池潭流域位于福建金溪中上游，汛期常受台风暴雨影响，其入库径流预测对金溪防灾预警和水与电力资源协调配置至关重要，而提前和准确的天气信息是池潭径流预测的关键基础。本文拟对TIGGE 资料中心的NCEP、ECMWF、JMA 和KMA 等四类预报产品在福建金溪池潭流域的预报效果进行评价，从降水分级预报、降水量级和降水过程预报等角度出发，综合评估多类产品的综合预测性能，并采用多种集成方法对比研究多模式降水集成预报在区域的适用性，以期更好地为区域防灾预警和资源配置决策提供支撑。

1 研究区域、资料与方法

1.1 研究区域

金溪为福建省闽江水系的二级支流，发源于杉岭山脉东部，其上游称宁溪，在西南部与其大支流杉溪汇合，称金溪。池潭水库位于金溪中上游，流域地理位置如图1 所示，其坝址以上控制流域面积4 766 km2，占整个金溪流域的66%，池潭水电站以上河长253 km，平均坡降0.15%。本文收集整理了池潭流域内18 个雨量站2014—2017 年的逐日降水，1 个国家基本气象站点1981—2017 年的逐日降水，各站点位置如图1 所示，站点的空间分布较为均匀，数据长度也满足产品评估需求。

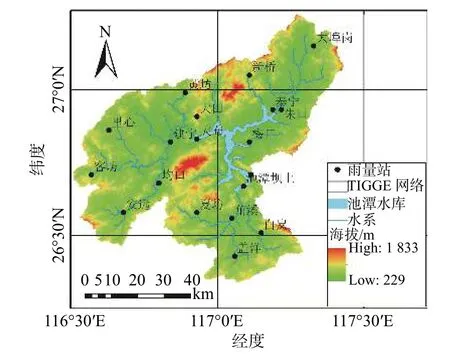
图 1 池潭流域及TIGGE 网格地理位置Fig. 1 Geographical location of Chitan watershed and TIGGE grid

1.2 资料来源及处理

交互式全球大集合系统（TIGGE）是世界天气研究计划的系统研究与可预报性试验THROPEX 计划的核心组成部分，旨在将全世界各国的气象业务中心集合预报产品集中起来，形成超级集合预报系统，并加速提高中短期1～14 d 预报时效上的预报精度[16-17]。本文选取了TIGGE 资料中心ECMWF、NCEP、JMA 和KMA 四种模式2014—2017 年的24 h （未来 1 d）控制预报产品作为检验和集成对象，模式基本信息见表1，预报数据空间分辨率为0.5°，统一选取世界时（Universal Time Coordinated，UTC） 00: 00 作为预报起点，这对应北京时间08: 00 （UTC+8: 00），正好与中国每日气象观测信息起点一致。覆盖流域的TIGGE 网格共有6 个，如图1 所示。控制预报数据可在网站http://apps.ecmwf.int/datasets/data/tigge/levtype=sfc/type=cf/进行下载。下载的模式数据格式为二进制格点数据(GRIB2)格式，可用资料中心提供的wgrib2.exe 解码得到相应的数据文本，具体解码命令可在Windows 命令提示符窗口下进行操作[18]。

本文统一采用网格平均和多站点算术平均提前将多模式降水和多站点实测降水处理为流域面平均降水，以此检验TIGGE 资料中心四种产品在池潭流域的日降水预报效果，并开展多模式降水集成预报研究。

表 1 数值预报产品基本信息Tab. 1 Basic information of the numerical prediction products

1.3 降水预报检验方法

1.3.1 降水分级预报检验 参考中国气象局雨量等级划分的标准，根据24 h 的降水量大小将降水量分为无雨（雨量＜0.1 mm）、小雨（0.1 mm ≤雨量＜10.0 mm）、中雨（10.0 mm ≤雨量＜25.0 mm）、大雨（25.0 mm ≤雨量＜50.0 mm）、暴雨以上（雨量≥50.0 mm）等5 个等级，并采用气象部门常用的《中短期天气预报质量检验办法》，利用TS 评分（临界成功指数）、BS 评分（预报偏差）、FAR（空报率）及PO（漏报率）这4 个评估指标来检验不同模式在降水分级预报中的表现，各指标计算公式如下：

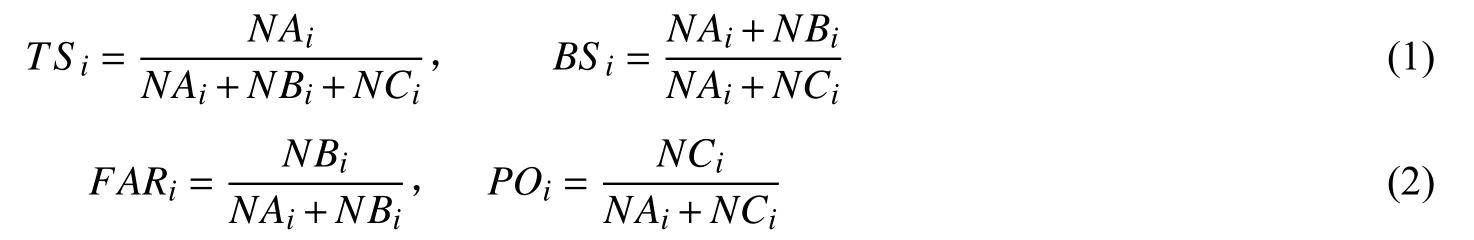
式中：i代表不同的降水量级；NAi为预报正确的次数；NBi为空报的次数（即预报了某量级降水而实际没有出现的情况）；NCi为漏报的次数（即没有预报某量级降水而实际却出现了的情况）。实况缺报或预报缺报，均不计入统计。

1.3.2 降水量预报检验 除降水分级预报效果评估外，对日降水量及过程预报进行整体评估也很有必要。本文采用AS 评分（Acceptable Score）检验降水量预报效果[19]。AS 评分是一个综合考虑绝对误差和相对误差的检验指标，其计算公式为：

式中：N1为预报系列中可接受的预报次数；N为总的预报次数。可接受预报的标准是满足条件：|Ea|≤Th或|Er|≤50%，Ea和Er分别为绝对误差和相对误差；Th为绝对误差的阈值，24 h 累积降水量的检验时取5 mm。

同时，利用检验雨量预报误差的常用指标：平均绝对误差（MAE）、均方根误差（RMSE）、预报偏小率（Sl）、预报偏小误差（Xl）、预报偏大（Sg）和预报偏大误差（Xg）来评估降水量预报效果，并采用Nash～Sutcliffe 效率系数（NSE）评估降水过程预报的整体效果。

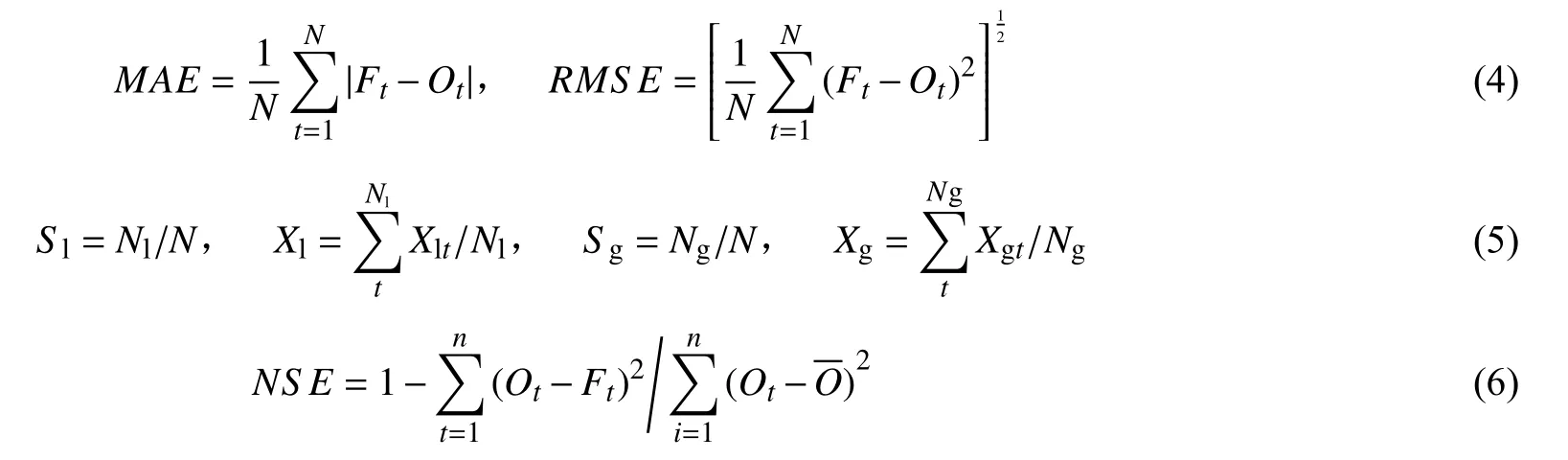
式中：Ft和Ot分别为第t天的预报降水和实测降水；N为总预报天数；Xlt为第t天降水偏小的误差；Xgt为第t天降水偏大的误差。若Ft＜Ot则预报偏小，Xlt=Ft-Ot，Nl为N天降水预报中偏小的总天数；反之若Ft＞Ot则预报偏大，Xgt=Ft-Ot，Ng为N天降水预报中偏大的总天数。平均绝对偏差（MAE）反映预报序列偏离实测的程度；均方根误差（RMSE）反映预报场和实况场差别的平均大小；预报偏小率（Sl）与偏小误差（Xl）、预报偏大

率（Sg）与偏大误差（Xg）分别反映降水预报值相对实测值的平均偏小和偏大程度。

1.4 降水集成方法

1.4.1 多元回归集成预报 多元回归集成预报法[20]是以各种预报产品为回归因子，以对应预报对象的实际观测值为集成变量，根据多元回归分析方法进行预报集成。目的是通过多元回归分析的拟合使集成变量能够最大程度地逼近预报对象的实际观测值

1.4.2 Nash 加权平均集成预报 Nash 效率系数NSE 加权平均法即以4 种模式的预报值和实测值之间的效率系数作为多模式集成的权重，计算公式如下：

式中：Wi为第i种模式的权重；m为参与集成的模式个数。

1.4.3 TS 分级加权平均集成预报 TS 评分分级加权法是以降水分级预报的TS 评分为权重，分别对不同量级降水进行加权。该方法是在NSE 系数加权平均法基础上的改进，不同量级降水赋予不同的权重值。传统的加权平均法（如平均权重法、效率系数加权平均法）均是根据相关指标值赋予某一种模式单个权重[21]，但由于不同模式对不同量级降水预报的效果存在一定差异，而单模式权重值仅可以反映该模式整体的预报效果，而无法体现模式对不同量级降水的预报差异，因此，本文以降水分级检验的TS 评分为依据构建了TS 评分分级加权平均法。计算方法如下所示：

式中：TSi,j为第i种模式j量级降水的TS 评分值；Wi,j为第i种模式j量级降水的TS 权重值；Pi,j为第i种模式j量级降水的降水量；Pj为j量级的多模式集成降水。

由于不同模式对同一天预报的降水量级可能不同，导致计算该天的集成降水时无法选取合适量级的TS 评分权重参与计算，故本文限定，当所有预报模式对该天的预报结果显示有一半以上均预报为某一量级降水时，则认定该量级的TS 评分权重为该天的权重值。

2 TIGGE 降水预报效果评估

2.1 降水分级预报

采用上述4 个评估指标，分析NCEP、ECMWF、JMA 和KMA 这四类预报模式对福建金溪池潭水库流域2014—2017 年不同降水量级的预报结果。由各等级降水的TS 评分结果图（图2）可知，各个模式无雨的TS 评分在0.40～0.60 之间，小雨的TS 评分在0.60～0.70 之间，说明各模式对无雨和小雨的预报能力均较高。对比空报率和漏报率变化图，小雨以上等级预报的TS 评分呈明显下降趋势，空报率和漏报率则显著增大，表明随着降水量级的增加，各个模式预报能力逐渐下降。从各等级降水的BS 评分来看，各个模式小雨和中雨的BS 评分均大于1，表明各个模式对小雨和中雨的预报误差主要来源于空报现象，反之，无雨、大雨、暴雨及以上等级的预报漏报现象较为严重。

对比各个模式的预报效果，可发现4 种模式在进行无雨预报时，预报效果JMA＞KMA＞ECMWF＞NCEP；进行小雨、中雨和大雨预报时，各个模式差别不大；当进行暴雨及以上量级的预报时，JMA 和KMA 模式TS 评分仅为0.10，显著低于其他两种模式（TS 评分在0.27 左右）。结合JMA 和KMA 模式BS 评分、空报率和漏报率变化情况可知，JMA 模式对暴雨及以上量级的预报漏报现象明显高于其他模式，Su 等[22]的研究也显示JMA 的暴雨预报量比其他中心要低得多，尤其是在较长的预见期内。

同时，由图2 TS 变化可知，JMA 和KMA 模式对无雨、小雨和中雨的预报效果均较好，小雨预报TS 评分高达0.69；而NCEP 和ECMWF 对大雨、暴雨及以上量级的预报效果最佳，暴雨及以上量级预报TS 评分达到0.27；ECMWF 模式对中雨以上量级的预报效果更优，其TS 评分均略高于其他模式。总体而言，进行25 mm 以下量级的降水预报时，JMA 模式最优，而对25 mm 以上量级降水的预报ECMWF 效果更好。

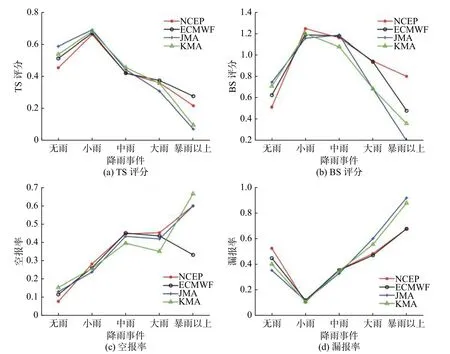
图 2 NCEP、ECMWF、JMA 和KMA 模式预报分级检验结果Fig. 2 Classification test results of NCEP, ECMWF, JMA and KMA model

2.2 不同时期日降水量预报

2.2.1 不同月份降水量预报检验 图3 给出了各个模式预报的平均绝对误差、均方根误差、AS 评分值和效率系数的逐月变化过程。从MAE 和RMSE 两类误差指标可以看出，4 种模式对各个月份降水量的预报效果不一，其中对5—6 月的降水量预报效果最差，预报的平均绝对误差达到7.5 mm 以上，均方根误差也高于15.0 mm；预报相对较好的月份如1—2 月、9—10 月和12 月等，其平均绝对误差基本低于3.0 mm，均方根误差也均低于5.0 mm。对比各个模式的预报误差，4 种模式除在9 月份的平均绝对误差和均方根误差有较为明显的差异外，在其他月份并无太大差异；并且，NCEP 模式在多数月份的平均绝对误差要高于其他3 种模式，而JMA 和ECMWF 模式的预报误差要略低于其他模式。因此从预报误差来看，4 种模式在预报各个月份的日降水量时效果差异不大，但整体而言JMA 和ECMWF 模式的预报效果更好一些。

从AS 评分和效率系数两类精度指标来看，精度指标随月份的分布情况和上文误差指标随月份的分布情况基本一致，4 种模式预报的效果随时间呈先下降再上升的变化特征。其中5—6 月模式预报降水的AS 评分均低于0.70，效率系数也均低于0.50，表明5—6 月份降水量预报最差；同时，根据效率系数的变化情况，4 种模式对于4 月、7 月和11 月的降水预报效果也相对比较差。对比各个模式的预报精度，从AS 评分来看，4 种模式之间的预报效果差异并不大，但从效率系数来看，模式间的差异较为明显，如3—4 月、7 月和9 月预报最好的模式和预报最差模式的效率系数差值均高于0.20，其中9 月份的效率系数差值更达到0.45 以上；并且，JMA 和ECMWF 模式在多数月份的预报精度要高于其他两种模式。总的来看，虽然不同指标对不同模式间的对比判别有所差异，但无论从误差指标还是精度指标的判定而言，JMA 和ECMWF 模式在预报各个月份日降水量时效果均要更好一些。

图 3 各个模式预报检验指标的月变化Fig. 3 Monthly variation of forecast verification indexes of each model

2.2.2 不同季节降水量预报检验 图4 给出了各个模式预报的平均绝对误差、均方根误差、AS 评分值和效率系数的季节变化过程。从MAE 和RMSE 两类误差指标可以看出，4 种模式在预报各个季节的日降水时具有明显差异，其中春季和冬季的平均绝对误差基本在1.2 和2.5 mm，均方根误差在3.0 和6.0 mm 左右，而夏季和秋季的平均绝对误差均高于5.0 mm，均方根误差也均高于11.0 mm。对比各个模式间的预报误差，4 种模式在预报春季日降水时，预报效果差异较小，预报其他季节日降水时差异较为明显，其中JMA 模式的平均绝对误差相对低于其他3 种模式，ECMWF 模式的均方根误差也相对低于其他模式。

从AS 评分和效率系数两类精度指标来看，精度指标随季节的分布情况和上文误差指标随季节的分布情况基本一致，4 种模式预报的效果随时间呈现先下降再上升的变化特征。预报较好的春季和冬季的AS 评分均高于0.85，而预报较差的夏季和秋季AS 评分均低于0.80，效率系数也均低于0.50，并且，各个模式对各个季节降水的预报效果各有差异，但整体而言，ECMWF 模式对各个季节的预报精度均优于其他模式。

不同模式在不同方面的表现存在一定的差异性，这与模型本身结构和配置方案有很大关联（表1）。比如相对其他模式，ECMWF 在结构上耦合了海洋模型，并且其垂直分层达到137 层（高度0.01 hPa），模式结构和模式分辨率相对其他模式更优，因而ECMWF 的综合表现更为稳健。

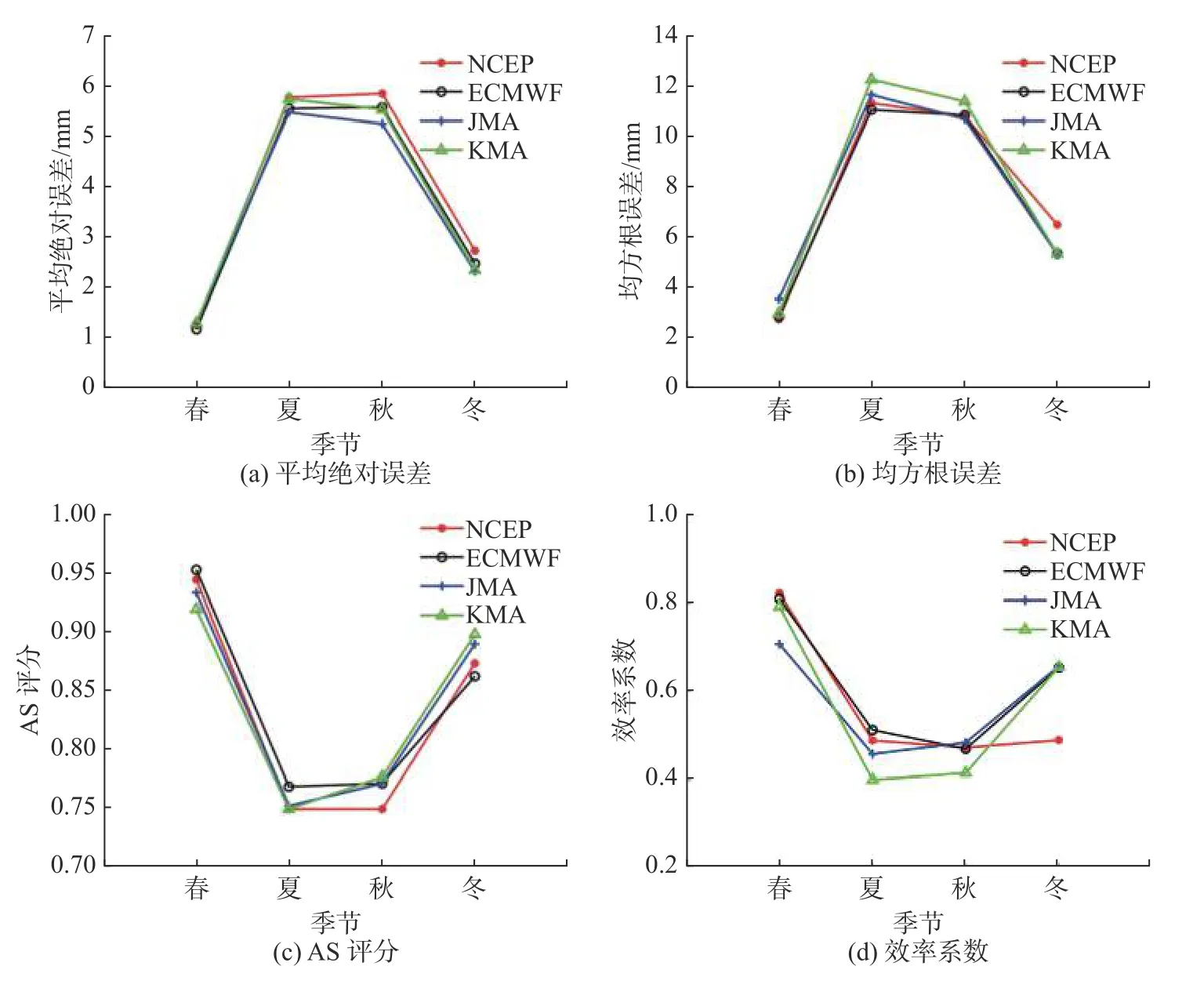
图 4 各个模式预报检验指标的季节变化Fig. 4 Seasonal variation of the forecast verification indexes of each model

3 多模式降水集成预报

选取TIGGE 中心的NCEP、ECMWF、JMA 和KMA 等4 种模式的2014—2017 年日降水预报数据为集成对象，采用多元回归集成、Nash 加权平均集成和TS 分级加权平均集成方法对4 种模式降水进行集成预报，并采用上文TS 评分、各类降水量及过程预报检验指标分析集成预报效果。TS 评分检验结果见图5。

图 5 集成预报与常规预报的降水分级TS 评分检验结果Fig. 5 The classification TS score test results of integrated forecast and conventional forecast products

由图5 可见，3 种集成方法对不同量级降水的集成效果各有差异，回归集成预报对无雨和小雨两种量级降水事件的预报效果较好，其TS 评分相对于该量级的单模式最优预报JMA 模式要高。Nash 加权平均集成预报相比于单模式预报，仅在中雨预报时其TS 评分大于该量级最优的单模式预报KMA 模式，而相较于其他两种集成预报，该方法的预报效果并无明显优势。相对而言，TS 分级加权平均集成预报对中雨、大雨、暴雨以上3 种降水事件的预报效果较好，其TS 评分相对于该量级的单模式最优预报均要高（大雨和暴雨以上的单模式最优预报为ECMWF 模式）。将集成预报同单模式预报进行对比可知，尽管部分集成预报并未比单模式最优预报效果要好，但集成预报对于各个量级的预报效果均优于大多数单模式模型，表明多模式集成预报能有效提高降水预报的稳定性。

降水量及过程预报检验指标如表2 所示。从MAE 和RMSE 这两个误差指标可以看出，NCEP、ECMWF、JMA 和KMA 这4 种模式的平均绝对误差和均方根误差的变化范围分别为3.9～4.3 mm、8.6～9.0 mm，而3 种集成预报方法的平均绝对误差和均方根误差的变化范围分别为3.6～3.7 mm、8.0～8.3 mm，整体相对于单模式预报的误差有所降低。从AS 和NS 两类精度指标可以看出，4 种单模式预报的AS 评分和效率系数的变化范围分别为0.81～0.83、0.49～0.55，而3 种集成预报的AS 评分和效率系数的变化范围分别为0.84～0.86、0.60～0.61，表明降水集成预报能够有效提高日降水量及过程预报的精度。对比4 种模式和3 种集成方法的偏小率、偏大率、偏小误差和偏大误差还可发现，7 种方法的偏大率均高于偏小率，而偏大误差均低于偏小误差，说明这4 种模式和3 种集成方法预报时偏大现象更多，但偏小幅度更为严重。分析可知，集成预报的偏大偏小误差现象主因在于4 种模式原始的预报偏差，尽管通过集成方法能从一定程度上降低整体降水预报的误差，提高降水预报精度，但由于集成方法本身考虑因素较少、原理简单，因而并不能较好解决此类偏大偏小误差现象。

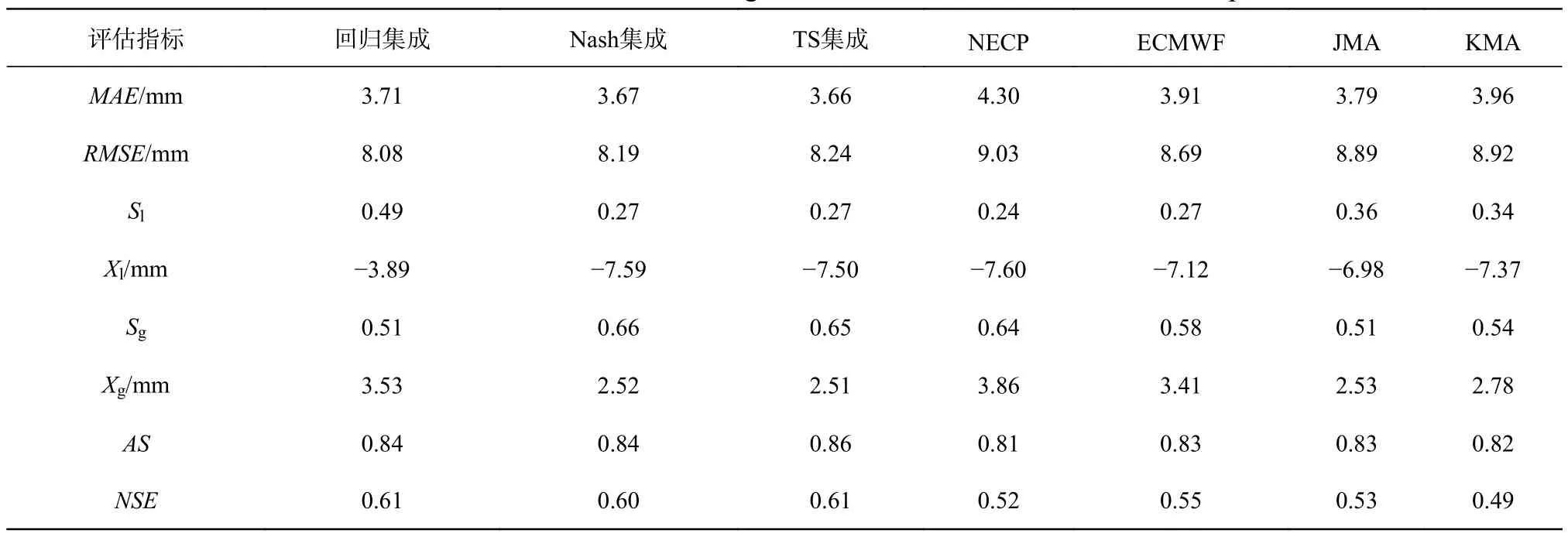
表 2 集成预报与常规预报产品检验指标统计Tab. 2 Verification index statistics of integrated forecast and conventional forecast products

对比3 种集成预报的MAE 和RMSE 误差指标，TS 集成的平均绝对误差最小，而回归集成方法的均方根误差最小；同时从AS 和NS 两类精度指标来看，TS 集成的AS 评分达到0.86，效率系数也达到0.61，表明TS 集成和回归集成两种方法的预报效果均较好。综合上文3 种集成方法的各量级降水TS 评分结果可知，利用这3 种方法进行降水集成预报时，预报效果优劣为：TS 集成＞回归集成＞Nash 集成。

4 结 语

以池潭流域为研究对象，对TIGGE 数据中心的ECMWF、NCEP、JMA 和KMA 模式2014—2017 年日降水预报数据进行了精度检验，采用多种评价指标分别从降水分级预报、降水量预报和过程预报等角度综合分析了单模式预报产品在池潭流域的适用性；并采用回归集成、TS 集成和Nash 系数集成等3 种方法对多模式产品开展了降水集成预报，在此基础上，探讨了不同集成方法对最终降水预报效果的影响，同时对比了单模式降水预报和基于多模式的降水集成预报的效果。结果表明：

（1）TIGGE 资料中心的4 种模式对无雨和小雨的预报效果较好，其TS 评分均高于0.45，而对暴雨及以上量级的降水预报效果较差，其中最优模式ECMWF 的TS 评分也仅为0.27；对比各个模式对各量级降水的预报效果，进行25 mm 以下量级的降水预报时，JMA 模式最优，而对于25 mm 以上量级降水的预报ECMWF 预报效果更好。

（2）对于日降水量的预报，NCEP 模式对日降水量的预报效果最差，而ECMWF 模式对日降水量的预报则最为精确，整体而言，这4 种模式预报时偏大现象更多，但偏小幅度更为严重。对于日降水过程的预报，KMA 模式的效率系数为0.49，而其他3 种模式效率系数均高于0.52，其中ECMWF 模式的效率系数最高，达0.55，表明ECMWF 模式对2014—2017 年金溪池潭水库流域的日降水过程的预报相对更为准确。

（3）集成预报对降低预报误差并提高降水过程预报有较好的效果，本文选用的3 种集成方法中，预报效果优劣为：TS 集成＞回归集成＞Nash 集成。TS 集成方法针对不同量级分类加权，较好地提升了高量级降水的预测效果。