多基地雷达栅栏覆盖的优化布站方法
李海鹏,冯大政,周永伟
(1.西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071;2.西安电子工程研究所,陕西 西安,710100)
无线传感器网络可用于解决区域监视问题,如何优化传感器的覆盖区域是其中一个研究重点。覆盖区域按覆盖类型可分为点覆盖、面覆盖和栅栏覆盖,其中栅栏覆盖应用较广[1]。文献[2]中首次提出了弱栅栏覆盖与强栅栏覆盖的概念。弱栅栏覆盖可以探测到沿垂直路径进入监测区域的入侵者,但不一定能探测到其他路径的入侵者;而强栅栏覆盖可以探测到以任意路径穿越到监测区域的入侵者。显然,强栅栏覆盖提供了更好的监测效果。随着雷达技术的不断发展,以雷达为传感器节点的栅栏覆盖问题引起了广泛关注。
根据雷达发射站与接收站的位置关系,雷达可以分为以下两种类型:发射站和接收站共置,即单基地雷达;多个(或一个)发射站和多个(或一个)接收站分置在距离较远的不同位置,即多基地雷达[3]。由于多基地雷达具有反隐身、抗反辐射导弹、抗电子干扰和抗超低空突防的优势[4-7],因此其栅栏覆盖问题成为了一个研究热点[8-11]。
文献[8]以克拉美罗下界的迹最小为优化布站准则,指出当接收站包围目标并呈等角布站时,对目标定位的克拉美罗下界取得最小值。但是对于目标运动,并不能保证接收站实时包围目标并呈等角分布,因此该方法不适用于探测运动目标。文献[9]研究了在不同接收站数量和目标位置的情况下,接收站布站对目标定位误差估计的影响,该方法仅优化了接收站位置,没有考虑发射站布站对优化性能的影响。文献[10]利用多基地雷达构建圆周栅栏覆盖,但是没有要求栅栏宽度不能为零,因此在栅栏覆盖上存在脆弱点。文献[11]构建了一种宽度不小于预定值的带状栅栏,用来覆盖矩形区域;同时考虑发射站和接收站的成本区别,以最小化布站总成本为目标,提出一种基于等分部署线的优化布站策略,即当需要多个部署线来覆盖被保护区域时,在每条部署线上均采用相同的布站序列,此种布站序列的两个端点至少有一处是发射站,甚至均为发射站。这种布站方式有两个不足:一是没有充分利用发射站,特别是当发射站成本远大于接收站成本时,发射站的成本浪费更明显;二是采用等分部署线的优化策略仅得到局部最优解。笔者旨在克服文献[11]中方法存在的不足,提出一种非等分栅栏覆盖的优化布站策略及求解算法。仿真结果表明,所提优化方法的布站总成本更低,且需要的发射站更少。
1 基本概念与理论
对于包含一对发射站T和接收站R的双基地雷达,空间任意一点z到接收站和发射站的直线距离分别记为RT和RR,接收站和发射站之间的距离L0称为基线。由于雷达经常工作于复杂电磁环境之下,在接收天线输出端的信号中除了有用的目标信号回波外,通常还包含杂波和干扰。因此,相干脉冲双基地雷达的基本方程为[12]
(1)
其中,Pav是发射平均功率,t0是相干积累时间,GR与GT分别是接收天线和发射天线的功率增益,λ是信号波长,FT与FR分别是目标至发射站与接收站路径的方向图传播因子,k是玻耳兹曼常数,T0是标准温度,Fn是接收机噪声系数,LT与LR分别是发射站和接收站的系统损耗,I0是干扰、杂波和热噪声在接收天线输出端产生的总能量,Emin/I0是检测目标信号所需的最小信干噪比(Signal-Inference-Noise Ratio,SINR)。假设目标雷达截面积σb不变,则Kb是由双基地雷达物理特性所确定的参数[13]。为书写方便,令γ0=Emin/I0。若目标在z点时接收天线输出端的信干噪比为γz,则当γz≥γ0时,认为该目标可以被检测到;反之,该目标不能被检测到。因此,满足γz≥γ0的z点所构成的区域是双基地雷达的覆盖区域。同时可知(RTRR)max=(Kb/γ0)1/2。令Lmax=((RTRR)max)1/2,称Lmax为等效单基最大距离。
由以上分析可知,双基地雷达的最大覆盖区域由一个焦点分别在接收站和发射站的卡西尼卵形线构成。覆盖区域的类型由参数L0和Lmax的关系决定[13],如图1所示。

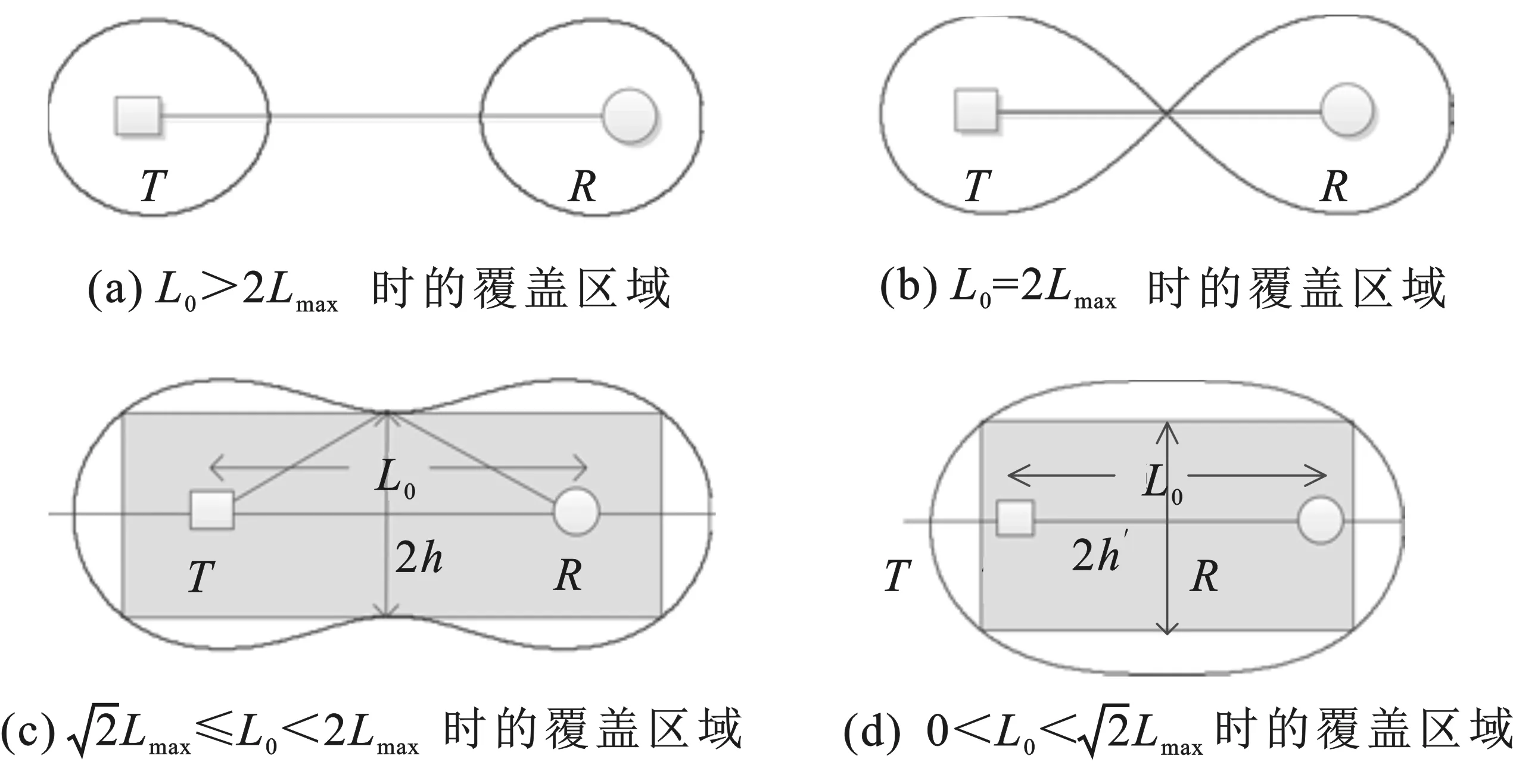
图1 双基地雷达覆盖区域类型
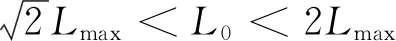

图2 栅栏覆盖长度示意图
(2)
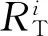
2 单条部署线的优化布站方法
为了求解布站问题,首先研究单条部署线上多基地雷达的栅栏覆盖特点。欲构成宽度为2h的栅栏覆盖,在一条部署线上依次连续部署1个发射站和m个接收站,构成布站模式Pm,记Pm=(Ti,R1,…,Rm),其栅栏覆盖的长度函数为ϖP(h,m)。在一条部署线上依次连续部署1个发射站、n个接收站和1个发射站,构成布站模式Fn,记Fn=(Ti,R1,…,Rn,Ti+1),其栅栏覆盖的长度函数为ϖF(h,n),如图2所示。相邻的Pm和Fn组成布站模式Gn,m=(Ti,R1,…,Rn,Ti+1,R1,…,Rm),其栅栏覆盖的长度函数为ϖG(h,n,m)。
由文献[11]可知,ϖP(h,m),ϖF(h,n)可分别按照以下公式计算:
(3)
(4)

由式(3)及式(4)可知,对给定的栅栏宽度2h,覆盖长度函数ϖF(h,n)和ϖP(h,m)是关于接收站数量的单调增函数,但是序列{dn,1≤n≤Nmax}是严格单调递减的[15],即随着接收站数量增大,覆盖长度的增幅逐渐减小。所以,虽然增加接收站的数量可以增加覆盖长度,但显然不是最优的布站方法。同时,为了避免部署线两端使用发射站,通过引理1说明部署线两端分别使用模式Pmi(i=1,2)的可行性,并证明|m1-m2|≤1是ϖP(h,m1)+ϖP(h,m2)的值取最大的充要条件。
引理1设m1,m2∈N*,max{m1,m2}≤Nmax,l=m1+m2,则
(1) ϖP(h,m1)+ϖP(h,m2)≤ϖF(h,m1+m2), 当且仅当m1=m2时等号成立。进一步有ϖP(h,m1)+ϖP(h,m2)的值取最大的充要条件是|m1-m2|≤1。

证明:(1)不失一般性,设m1≤m2,若m1+m2为奇数,由式(3)及式(4),有
(5)
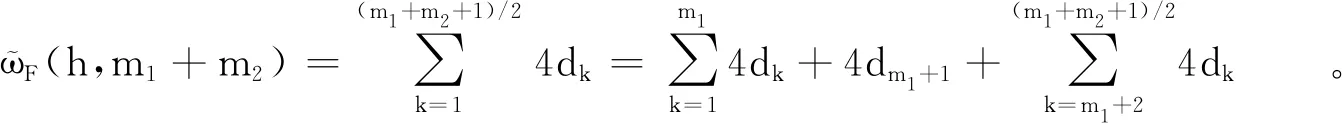
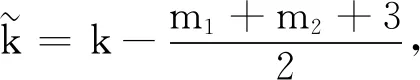
(6)
同理,当m1+m2为偶数时,有
(7)
由序列dk的递减性及式(6)~(7)可得ϖP(h,m1)+ϖP(h,m2)≤ϖF(h,m1+m2)。值得注意的是:若m1+m2为偶数,由式(7)可知,当且仅当m1=m2时,ϖP(h,m1)+ϖP(h,m2)的值取得最大值ϖF(h,m1+m2);若m1+m2为奇数,由式(6)可知,仅当m2=m1+1时,ϖP(h,m1)+ϖP(h,m2)的值取得最大值ϖF(h,2m1+1)-(xm1-xm1+1)。综上,ϖP(h,m1)+ϖP(h,m2)的值取最大的充要条件是|m1-m2|≤1。
(2)若l=2v-1为奇数,则由式(3)及式(4)分别可得
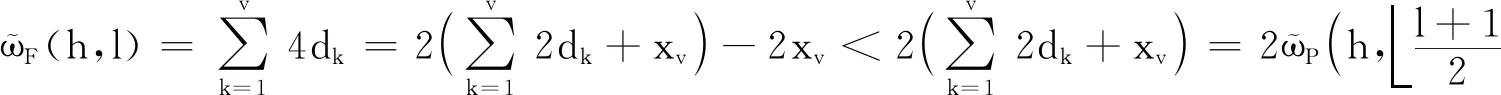
同理,当l=2v,即为偶数时,有

引理1进一步表明:若模式Fn中接收站数量n为奇数,那么其覆盖长度大于模式P(n+1)/2与P(n-1)/2的覆盖长度之和,小于两个模式P(n+1)/2的覆盖长度之和。因此,可以用两个模式P(n+1)/2替代1个模式Fn;若n为偶数,则可以用两个模式Pn/2等量替代1个模式Fn,且这种替代是最优的。

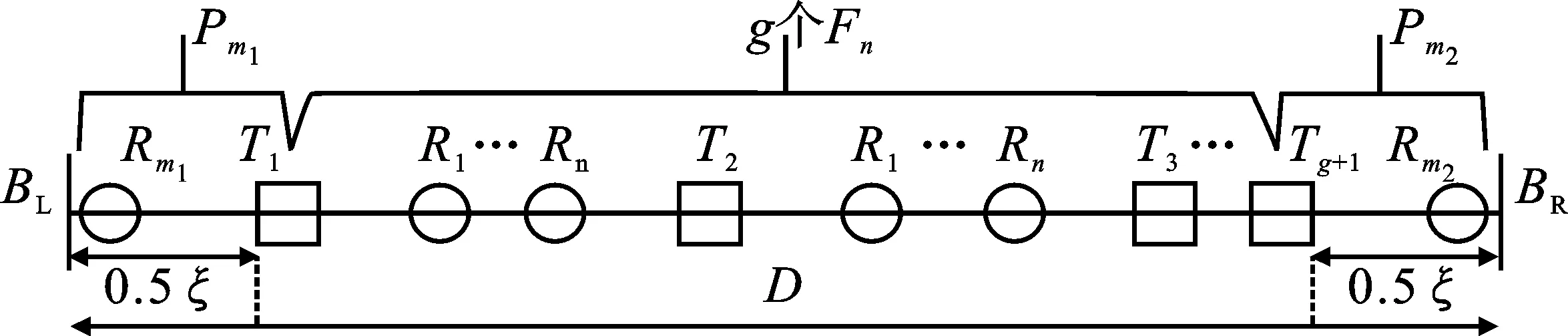
图3 单条部署线的模式布置示意图

(8)
易知对于给定的n,m,ϖF(h,n)与ϖP(h,m)分别是关于h在某个区间的单调递减连续函数。由于LS(h)是ϖF(h,n),ϖP(h,m1)和ϖP(h,m2)的线性组合,因此LS(h)也是关于h的单调递减连续函数。所以对于给定的布站序列,其覆盖的长度越大,则覆盖的栅栏宽度越小;也即在保证覆盖长度满足需求的条件下,总有一个栅栏覆盖宽度最大的布站序列。在优化布站策略中,一般选择覆盖长度不小于给定值且覆盖宽度最大的栅栏。
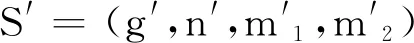
以下通过引理2表明对于非等分栅栏覆盖矩形区域,栅栏宽度的可能取值为有限多个。

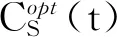
不妨设接收站成本单位为1,则图4给出α=5时,最优部署成本函数Copt(t)的图像(局部)。可以看出,当栅栏宽度变化时,其需要的部署费用并不一定随之改变。也就是说,同样的部署成本可以对应不同的栅栏宽度。因此从优化费效比的角度来说,应当选择其中宽度最大的栅栏,最终优化布站结果是这些非等分栅栏的线性组合。
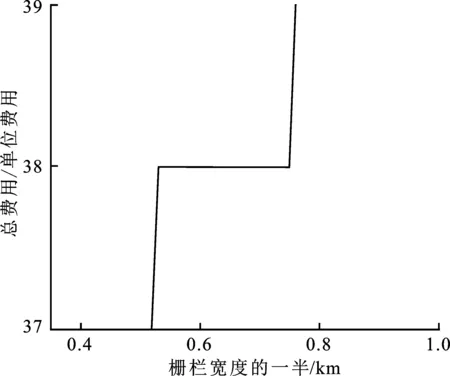
图4 当α=5时最优部署成本函数的曲线图
因此,对于给定的h,单条部署线的优化问题为
(9)
式(9)的解就是单条部署线覆盖区域2h×D的最优覆盖序列,即单条部署线的最优布站序列。
3 矩形区域的优化布站策略与算法
采用非等分部署线的布站策略,即从宽度上将矩形区域划分成若干个小矩形(各小矩形的宽可以不相等,但小矩形的长与矩形区域长相等),每条部署线布站的方式也不相同,其中单条部署线上布站的方式如图3所示。
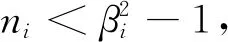
(10)

(11)
至此,式(11)所示优化问题可转化为以下两个子优化问题。
子优化问题1(hi给定):
(12)

子优化问题2:
(13)
采用分层方法求解式(11)所示的优化问题,即利用穷举法求解式(12)和整数线性规划方法[16]求解式(13)。
笔者所提算法的伪码表示如下。
输入:等效单基最大距离Lmax,发射站与接收站费用比α,覆盖矩形区域的宽度H及长度D。

② forhi=hmin∶η∶hmax,η是栅栏宽度变化步长;

④ 循环结束;

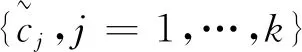
说明:
(1)子优化问题1的求解过程。

② forn=1∶1∶Nmax;
③ 计算两端Pl与Pr模式中接收站的个数r,l,以及此时单条栅栏的部署费用:

④ 循环结束;
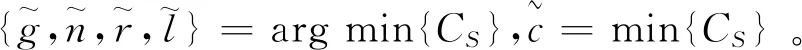
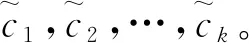
4 仿真实验
以下通过仿真实验说明所提算法的有效性。仿真实验基本假设同文献[11],等效单基最大距离Lmax=4 km,单条部署线所构建的栅栏宽度最小阈值2τ=0.6 km。矩形长度D=100 km不变,矩形宽度H由 4 km 增加到25 km,步长为1 km。对费用比α=1,20,70的情况分别进行仿真,并与文献[11]的结果进行比较。为便于叙述,将文献[11]的优化布站方法称为“文献[11]方法”、笔者所提优化布站方法称为“文中方法”。费用减少率定义如下:费用减少率η=100%×(C1-C2)/C2,其中C1,C2分别是文献[11]方法和文中方法得到的优化布站总费用,费用减少率曲线如图5所示。
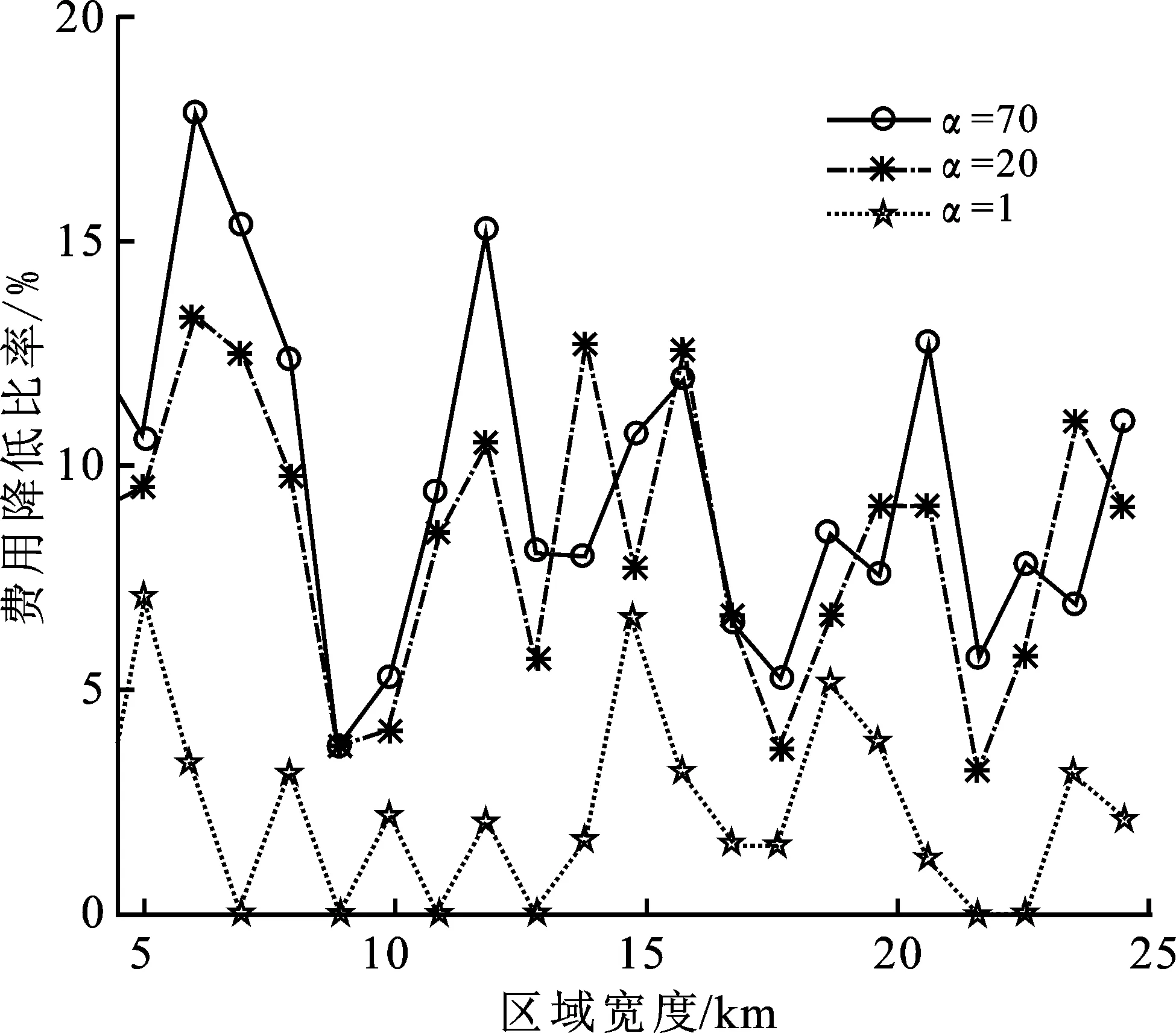
图5 α=1,20,70时费用降低率曲线图
由图5可知在不同费用比下,费用减少率均不小于零,因此相比于文献[11]方法的部署成本,文中方法的布站总费用更低。即使在发射站费用与接收站费用之比α=1时,文中方法也能取得更低的部署成本,这些说明了文中方法的有效性。值得注意的是,当α=1时,两种方法的优化结果在有些宽度情况下相等,此时发射站并不存在成本优势,文中优化方法的特点是最大化发射站的成本。在实际应用中,发射站成本远大于接收站的。
下面给出在α=1,20,70时,针对不同区域宽度,文献[11]方法与文中方法的发射站需求数量差,如图6所示。从图6可以看出,发射器总量差均不小于零,说明文中方法需求的发射站数量不多于文献[11]方法的。由于有源的发射站容易被干扰和定位,采用更少的发射站有利于多基地雷达系统在电子战中发挥效能,降低风险。
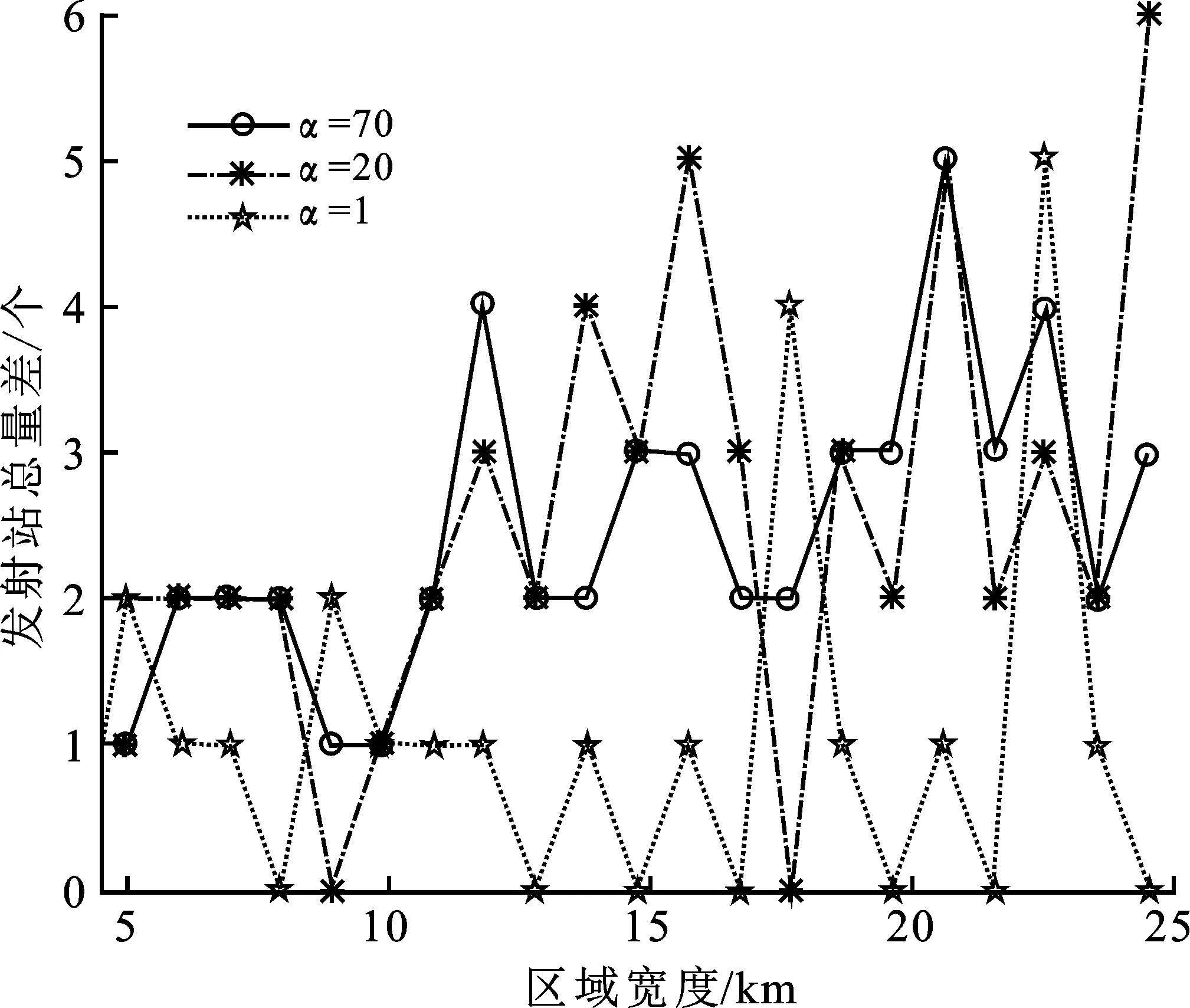
图6 α=1,20,70时发射站总量差曲线图
下面以α=20,D=100 km为例说明文中方法的布站结果,如表1所示。

表1 α=20,D=100 km时文中方法的优化布站结果
表1中,H、C、q、h、n、l、r、g、M、N、DL分别表示矩形宽度、优化布站的总费用、不同栅栏数量、半栅栏宽度、模式Fn中接收站数量、模式Pl与Pr中接收站数量、模式Fn的数量及单条部署线上发射站与接收站的数量、实际栅栏覆盖的长度。
表1说明在α=20的情况下,为了覆盖一个宽度H=14 km,长度D=100 km的矩形区域,按照文中方法所得的布站结果。具体来说:当半栅栏宽度h=2.10 km,即单条整栅栏宽度为4.2 km时,对应的栅栏数量q=2个,模式Fn中接收站数量n=2个,且模式Fn的数量g=6个。同时,模式Pt与Pr中接收站数量分别为l=1个和r=1个。因此单条部署线上接收站数量N=q(gn+l+r)=2×(6×2+1+1)=28个,发射站数量m=q(g+1)=2×(6+1)=14个。类似可知,当半栅栏宽度h=1.50 km,即单条整栅栏宽度为 3.0 km 时,布站结果为:部署线中间使用4个模式F4,部署线两端分别使用一个模式P2,需要发射站5个,接收站20个。当半栅栏宽度h=1.28 km,即单条整栅栏宽度为2.56 km时,布站结果为:部署线中间使用4个模式F3,部署线两端分别使用有一个模式P1与P2,需要发射站5个,接收站15个。共计需要发射站 24个,接收站63个;相应地,由式(2)可知布站总费用为543个单位费用。
5 结束语
在最小部署费用的准则下,基于区域覆盖研究了多基地雷达的优化布站问题。在栅栏宽度一定时,通过理论分析说明了布站模式的覆盖特点,并提出了单条栅栏覆盖的优化布站序列。进而采用非等分栅栏的布站策略覆盖给定的矩形区域,分别利用整数线性规划与穷举搜索确定最小部署成本及对应的布站参数。最后通过仿真,表明笔者提出的方法可以在满足覆盖需求的情况下,获得更低的部署成本和使用更少的发射站。

