非自治随机p-Laplacian格点方程的后向紧随机吸引子

宋 立，李扬荣

西南大学 数学与统计学院， 重庆 400715

若随机吸引子的后向并是预紧的， 则称该吸引子为后向紧随机吸引子． 文献[1-2]对非自治动力系统所产生的拉回吸引子的存在性和后向紧性做了深入的研究， 并建立了相对完善的理论体系． 文献[3-6]对非自治方程的吸引子的存在性进行了研究， 文献[7-8]对自治p-Laplacian格点方程吸引子的存在性做了研究． 本文将在文献[8]的基础上， 研究非自治情况下， 带有乘法噪音的随机p-Laplacian格点方程的后向紧吸引子的存在性．

1 预备知识

θt(s+t， ·)=θt(t， ·)∘θt(s， ·) ∀t，s∈R

则称(Ω， F，P，θ)是一个度量动力系统．

则称映射Φ是关于(Ω， F，P，θ)的非自治动力系统， 也称协循环．

定义4令B是X的所有有界非空子集族构成的集合， 假设集合

K={K(τ，ω)：τ∈R，ω∈Ω}∈B

若对任意的τ∈R，ω∈Ω，D∈B， 存在T=T(τ，ω，D)>0， 使得当t≥T时有

Φ(t，τ-t，θ-tω，D(τ-t，θ-tω))⊆K(τ，ω)

则称K为Φ的B-拉回吸收集．

2 非自治随机动力系统

本文将在l2空间上讨论带有乘法噪音的非自治随机p-Laplacian格点方程

(1)

其中Z代表整数集，λ，α>0，p>2，W(t)是双边实值Wiener过程， ∘代表Stratonovich积分意义下的乘法噪音． 对于外力项f=(fi)i∈Z和非自治项g=(gi)i∈Z有如下假设：

fi(s)s≤0 ∀s∈R

(2)

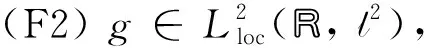
(3)

(4)

定义l2上的有界算子：

B： (Bu)i=ui+1-uiB*： (B*u)i=ui-1-ui

A： (Au)i=|ui-ui-1|p-2(ui-ui-1)-|ui+1-ui|p-2(ui+1-ui) ∀u∈l2

因此， 根据算子的定义， 有

(5)

微分方程(1)可整理为

(6)

下面证明方程(6)能生成随机动力系统．

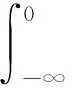
(7)

因此方程(6)可转化为关于v的随机微分方程

(8)

由文献[8]可知， 对任意T>0，v0∈l2，ω∈Ω， 方程(8)存在唯一的解v(·，τ，ω，v0)∈C([τ， +∞)， l2)， 且依赖初值v0连续． 因此方程(8)在(Ω， F，P， {θt}t∈R)上能生成一个连续的随机动力系统{Φ(t)}t≥0， 即对v0∈l2，t≥0，τ∈R， 和ω∈Ω， 有

Φ(t，τ，ω，v0)=v(t+τ，τ，θ-τω，v0)

在下文中， 设D0是X中所有缓增集构成的集合， D是X中所有后向缓增集构成的集合． 若集合D0满足

(9)

则称集合D0为缓增集； 若集合D满足

(10)

则称集合D为后向缓增集．

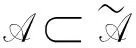
3 解的估计

引理1若假设(F1)，(F2)成立， 那么有：

(11)

其中R0(τ，ω)是可测函数， 定义为

(12)

(13)

其中

(14)

证对任意固定的τ∈R，ω∈Ω，vs-t∈D(s-t，θ-tω)， 令v(r)=v(r，s-t，θ-sω，vs-t)， 其中s≤τ．v(r)与方程(8)作内积可得

(15)

利用(2)，(5)式整理(15)式， 可得

(16)

利用Hölder不等式及Young不等式， 有

(17)

代入(16)式可得

(18)

对(18)式利用Gronwall不等式， 计算可得

(19)

再由(7)式、 (9)式可知， 存在T0(D0，s，ω)≥1， 使得当t≥T0时， 有

(20)

因此(11)式得证．

对(19)式关于s∈(-∞，τ]取上确界， 由于vs-t∈D(s-t，θ-tω)(s≤τ)， 结合(7)式、 (10)式可知， 存在T=T(s，ω， D)≥1， 使得当t≥T时， 有

(21)

因此可以得到

(22)

即(13)式得证．

注射碘酊治疗组:1周后,囊肿注射部位的粘膜表面发白,无触痛,3周后,注射部位与周围粘膜无差异,囊肿已完全消失,表面粘膜未见异常,半年内进行随访,见6例囊肿复发。

引理2若假设(F1)，(F2)成立， 则有如下结论：

K0(τ，ω)={w∈l2： ‖w‖2≤1+R0(τ，ω)} ∀τ∈R，ω∈Ω

(23)

(24)

首先证明R(τ，ω)是有限的． 根据(7)式可知， 对任意ε>0， 存在C=C(ε，ω)>0， 使得

(25)

(26)

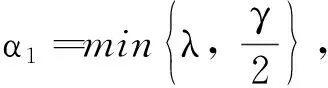
(27)

所以K∈D0． 又由于K0⊂K， 因此K0∈D0．

最后证明K∈D． 根据(24)式， 易知集合K是递增的， 即

K(τ1，ω)⊂K(τ2，ω) ∀τ1<τ2

因此， 结合K∈D0可知， 对任意γ>0， 有

(28)

即证得K∈D． 再由(13)式可知， K在任意集合D∈D上是后向一致吸收的．

引理3若假设(F1)，(F2)成立， 则对∀ε>0， (τ，ω， D)∈(R×Ω×D)，vs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，N(ε，τ，ω， D)≥1， 使得

证构造光滑函数ρ， 满足0≤ρ≤1， 且当|s|≤1时，ρ=0； 当|s|≥2时，ρ=1． 并假设存在常数c0， 使得对任意s∈R， 有|ρ′(s)|≤c0． 令N是一个固定的整数， 设

x与(8)式作内积可得

其中

(29)

由于|ρ′(s)|≤c0， 因此

(30)

故由(29)式、 (30)式可得

(31)

由假设(F1)可知

(32)

由Young不等式可知

(33)

结合(31)-(33)式， 可得

(34)

对(34)式运用Gronwall引理， 计算整理可得

(35)

由于vs-t∈D(s-t，θ-tω)(s≤τ)， 结合(7)，(10)式可得

(36)

(37)

(38)

因此， 结合(36)-(38)式可得， 对任意的ε>0， (τ，ω， D)∈(R×Ω×D)，vs-t∈D(s-t，θ-tω)， 存在T(ε，τ，ω， D)>0，N(ε，τ，ω， D)≥1， 使得

引理4若假设(F1)，(F2)成立， 则协循环{Φ(t)}t≥0在吸收集K∈D上是后向渐近紧的．

证对任意固定的τ∈R，ω∈Ω， 取任意序列{τk}≤τ， {tk}→+∞(k→+∞)， 及任意的v0∈K(τk-tk，θ-tkω)． 定义vk=Φ(tk，τk-tk，θ-tkω，v0)=v(τk，τk-tk，θ-τkω，v0)， 下证{vk：k∈N}在l2中是预紧的．

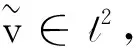
(39)

下面只需证明该弱收敛实际上是强收敛， 即只需证明：

对任意ε>0， 存在T>0和K≥1， 使得当k>K时， 有

(40)

注意到

(41)

一方面， 由引理3可知， 对任意ε>0， 存在T1>0，N1，K1≥1， 使得当k>K1时， 有

(42)

(43)

由(42)-(44)式可知， 令

即证得协循环{Φ(t)}t≥0在吸收集K上是后向渐近紧的．

4 后向紧随机吸引子

定理1若假设(F1)，(F2)成立， 则方程(1)生成的动力系统存在后向紧随机吸引子．

证引理2和引理4的结论满足了文献[11]的定理3.9中拉回吸引子的存在性条件， 因此方程(8)生成的非自治随机动力系统Φ(t)存在唯一的后向紧D-拉回吸引子A∈D， 和唯一的可测D0-拉回吸引子A0∈D0． 再由文献[9]的定理6.1知A=A0， 故吸引子A也是随机的， 即Φ(t)存在唯一的后向紧D-拉回随机吸引子A∈D． 再由文献[12-13]知方程(1)与方程(8)生成的随机动力系统共轭， 进而可知方程(1)存在后向紧随机吸引子．