一种基于多重特征融合的信源个数估计方法

张冰玉，潘 晴，田妮莉，Everett Xiaolin Wang

（广东工业大学信息工程学院，广州 510006）

0 概述

在阵列信号处理过程中，空间谱表示信号在空间各个方向的能量分布［1］，常用的空间谱估计算法有旋转不变子空间（Estimating Signal Parameters via Rotational Invariance Techniques，ESPRIT）算法［2］、多重信号分类（Multiple Signal Classification，MUSIC）算法［3］和相关改进算法［4-5］，这些算法都是以事先已知信源的个数为前提条件。目前，信源个数估计多使用基于信息论准则的方法，包括最小信息准则（Akaike Information Criterion，AIC）［6］、最小描述长度（Minimum Description Length，MDL）准则［7］及相关改进算法［8-9］，但这些算法仅适用于白噪声环境下的信源个数估计。

适用于色噪声环境的盖尔圆估计（Gerschgorin Disk Estimation，GDE）准则［10］虽然能够弥补信息论准则在色噪声环境下信源个数估计失效的不足，但其在低信噪比和小快拍数条件下的性能会急剧下降甚至失效。针对该问题，文献［11］提出一种新的酉变换方法，并结合GDE 准则进行信源个数估计。实验结果表明，该方法在快拍数为90 时的信源个数检测准确率达到90%，但是要求信噪比在10 dB 以上。文献［12］将GDE 准则和AIC 准则结合，克服了特征值的无序性导致估计错误的缺陷，使得检测准确率在信噪比为−5 dB 时达到93%，但该方法要求较大的快拍数。文献［13］对盖尔圆半径进行压缩，并结合盖尔圆心值提出一种基于自适应调整因子的GDE准则。实验结果表明，该方法在信噪比为−4 dB、快拍数大于2 000 的条件下检测准确率为80%，而在信噪比为15 dB、快拍数为50 时检测准确率达到90%。由此可知，该方法无法同时保证低信噪比和小快拍数条件下的检测性能。文献［14］利用接收信号协方差矩阵的对角线平均值来构建新的协方差矩阵，并结合GDE 准则估计信号源数。该算法在非平稳的色噪声环境中，信噪比为−8 dB、快拍数为100 时的检测准确率就已经达到80%以上，虽然能同时保证低信噪比和小快拍数情况下的高检测准确率，但仅限于在10 个阵元估计2 个信源的条件下。文献［15］基于Khatri-Rao 积先对接收信号的协方差矩阵做延迟处理后再对矩阵进行矢量化来构造新的矩阵，并结合盖尔圆准则估计信源数。该方法虽然能在M个阵元下至多估计出(2M-1)个信号源，但仅限于在白噪声条件下，具有一定的局限性。

上述GDE 准则及改进方法对于含M个阵元的阵列，在构造盖尔圆盘过程中都只用到了前（M-1）个阵元接收的信息，导致这些方法能估计的最大信源个数为M-2。文献［16］提出了加权盖尔圆估计（Weighted Gerschgorin Disk Estimation，WGDE）准则，由于该准则中的特征加权矩阵对增广盖尔圆矩阵中的盖尔圆半径做特征加权变换，因此进一步增大了信号盖尔圆和噪声盖尔圆之间半径的差异，使快拍数为64 时的信源估计准确率达到90%，但是信噪比要求为13 dB。同时，WGDE 准则在构造增广盖尔圆矩阵及其增广加权盖尔圆矩阵过程中都保留了M个阵元的信息，这使得估计(M-1)个信号源数成为可能。文献［17］将信源数估计问题转为模式识别问题，依据阵元在接收含有不同信源个数的入射信号时会产生不同相位差异这一特点，结合希尔伯特-黄变换（Hilbert-Huang Transformation，HHT）和SVM 进行信源个数估计，从而利用M个阵元估计（M-1）个信号源数，但该文并未对快拍数小于100时的信源数估计性能进行验证。

本文结合文献［17］方法，针对WGDE 准则对增广加权盖尔圆矩阵信息利用不足的缺陷，提出一种在增广加权盖尔圆矩阵中获取多重特征并融合的信源个数估计方法。同时获取可用于描述信源个数的盖尔圆心值、盖尔圆半径和加权盖尔圆半径等多重特征进行融合，构建能够描述信源个数的高维特征向量，标定后代入支持向量机（Support Vector Machine，SVM）中训练可用于信源个数估计的分类器，并利用包含M个天线的均匀圆阵（Uniform Circular Array，UCA）（下文简称M-UCA）进行仿真实验。

1 M-UCA 的接收信号模型

假设k个远场窄带信号入射到M-UCA 上，其中k=1，2，…，K且K＜M，则M-UCA 接收信号表示为：

其中，X(t)=[x1(t)，x2(t)，…，xM(t)]T为t时刻的接收信号矢量，S(t)=[s1(t)，s2(t)，…，sk(t)]T为t时刻信号的源矢量，N(t)=[n1(t)，n2(t)，…，nM(t)]T为t时刻加性噪声矢量，A=[α(Θ1)，α(Θ2)，…，α(ΘK)]为M-UCA的阵列流型矢量，Θk=(φk，ϑk)为第k个信号源的入射角，φk和ϑk分别为第k个信号源的方位角和俯仰角，且为第k个信号源的导向矢量，其中为逆时针第m个阵元与x轴的夹角，，m=1，2，…，M，为载波波长。

2 增广加权盖尔圆矩阵与加权盖尔圆准则

在满足奈奎斯特采样定理［18］的条件下，对X(t)做快拍数为L的均匀采样，获得X(t)的观测信号数据集X(l)，l=1，2，…，L且X(l)=[x1(1)，x2(2)，…，xM(l)]T，则观测信号数据集的协方差矩阵为：

其中，(⋅)H表示共轭转置。对Rxx做特征分解得到：

其中，λm为Rxx的第m个特征值，λ1＞λ2＞，…，＞λk-1＞λk＞＞，…，＞λM，当m≤k时，λm为信号特征值，反之为噪声特征值，um为λm所对应的特征向量。定义如式（4）所示的矩阵：

其中，r为Rxx的最后一列向量。定义酉变换矩阵T如式（5）所示：

其中，u=[u1，u2，…，uM]T。经过如式（6）所示的酉变换计算得到增广盖尔圆矩阵RG：

其中，Σ为所有λm组成的对角阵。定义特征加权矩阵W如式（7）所示：

对RG做特征加权变换，得到增广加权盖尔圆矩阵RF，如式（8）所示：

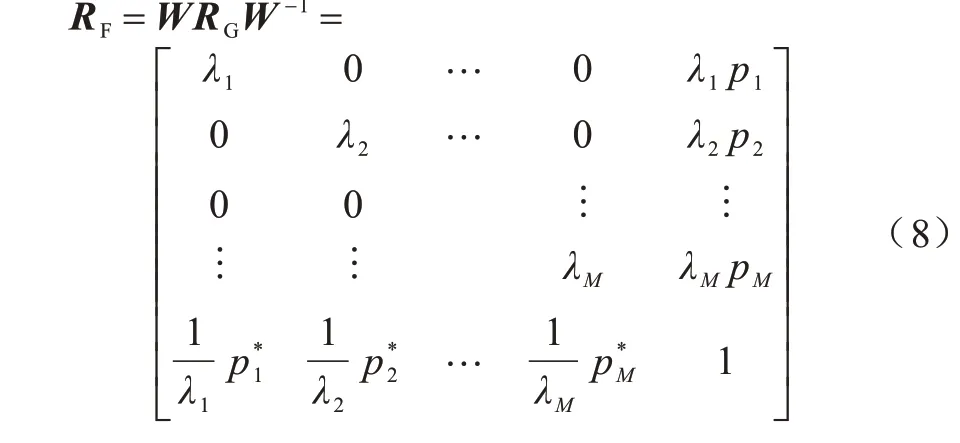
令rm=λm pm，得到判别准则为：

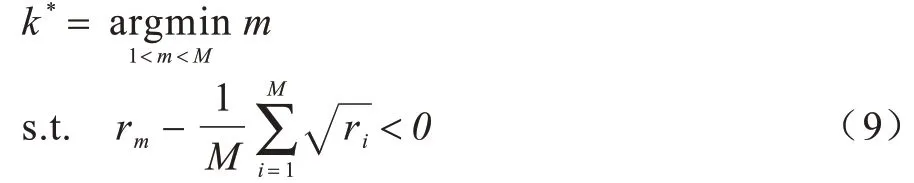
则利用WGDE准则得到的最终信源估计个数为：

3 增广加权盖尔圆矩阵多重特征融合及建模

在增广加权盖尔圆矩阵RF中包含了pm、λm、rm3 种用于信源个数估计的特征，分别表示盖尔圆心、盖尔圆半径和加权盖尔圆半径，其中，AIC 准则利用λm对信源个数进行估计［6］，GDE 准则利用pm对信源个数进行估计［10］，而WGDE 准则利用rm对信源个数进行估计［16］，显然WGDE 准则对RW中的特征应用并不充分。因此，本文将上述都能用于信源个数估计的3 种特征进行融合，构建3M维的特征列向量θ，如式（11）所示：

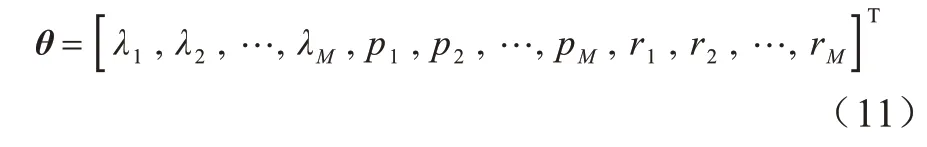
分别对式（11）中的各特征做归一化处理，如式（12）～式（14）所示：

在式（16）中，g为高斯径向基函数的核参数，φ：ℝ3M→ℝS，且有：

本文模式分类的SVM 设计通过寻找以下优化问题的解来实现：

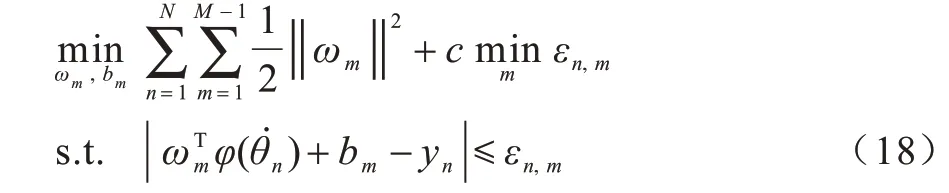
其中，ωm，bm∈ℝS，c为惩罚因子，εn，m为松弛变量。由于式（18）中的最优解为，因此本文利用Libsvm 工具包在寻优的过程中同时求解最优的参数对(c*，g*)，从而提高对训练数据集的识别率。

4 仿真实验及分析

4.1 数学模型训练

实验采用4-UCA 作为接收信号阵列，阵元间距为载波波长的1/2，3 个远场窄带信号源的入射角随机设置，分别为(0°，25°)、(29°，69°)和(60°，106°)，信噪比为-7 dB，采样快拍数L=120，在色噪声条件下［19］，随机选取信源数分别为1、2、3 时的各1 000 个样本生成特征向量并标定，放入Libsvm 中训练，令lbg∈[-10，10]、lbc∈[-10，20]，搜索步长为1，采用10 倍交叉验证法［20］寻找(c*，g*)，寻优过程的二维等高线图和三维等高线图分别如图1（a）和图1（b）所示，其中，lbc*=18，lbg*=-4，此时的估计准确率约为92.2%，从而获得能够进行信源个数估计的4-UCA 数学模型。

图1 基于4-UCA 的SVM 模型在不同网格点上寻优参数对时的准确率等高线图Fig.1 Contour map of the accuracy rate when SVM model searches optimal parameter pairs based on 4-UCA at different grid points

4.2 仿真实验

实验1不同快拍数下信源个数估计的对比实验

选取4-UCA 接收的包含1 个、2 个和3 个信号源的测试样本各200 个，且测试样本与训练样本的入射角不同，信噪比为0 dB，快拍数L从40 增加到200，步长为20，将本文方法与文献［10］提出的GDE 方法、文献［12］提出的改进GDE 算法（此处记为GDE_AIC 方法）、文献［16］提出的WGDE 方法以及文献［17］方法（此处记为HHT_SVM 方法）做对比实验，针对不同拍数下采集的测试样本，每个方法重复Monte Carlo 实验［21］200 次。分别对含1 个、2 个和3 个信号源的阵列信号做测试，得到5 种方法在不同快拍数下的检测准确率。

实验2不同信噪比下信源个数估计的对比实验

实验中的条件除了L=100，SNR 范围为−20 dB～20 dB，步长为5 dB外，其他条件与实验1相同，得到5种方法对不同信噪比阵列信号的检测准确率。

4.3 结果分析

实验1 的检测准确率对比如图2 所示，可以看出：当信号源个数为1 和2 时，在快拍数L≤200 条件下，GDE 方法、MGDE 方法、WGDE 方法失效，GDE_AIC 有一定的检测准确率但最高只有72%，而本文方法则表现出优异的检测性能，当L＞90 时，对信号源个数的检测准确率就已经超过了90%；当信号源为3 时，GDE 方法、MGDE 方法、WGDE 方法、GDE_AIC 方法完全失效，本文方法在快拍数L=60时检测准确率就达到了80%；HHT_SVM 方法只是在L≥100 时才表现出检测性能优于本文方法。

图2 5 种方法在不同快拍数下的检测准确率对比Fig.2 Comparison of the detection accuracy of five methods under different snapshot numbers

实验2 的检测准确率对比如图3 所示，可以看出：当信号源个数为1 和2 时，GDE 方法和WGDE 方法在信噪比大于等于7 dB 时才能获得80%以上的检测准确率，GDE_AIC 方法在信噪比大于等于5 dB 时的检测准确率达到90%以上，而本文方法在信噪比为-20 dB 时检测准确率就已经达到80%，且检测准确率随着信噪比的提高而稳步提高；当信源个数为3 时，GDE 方法、WGDE 方法、GDE_AIC 方法失效，本文方法则始终保持较高的检测准确率；HHT_SVM 方法的检测性能优越一直保持在80%以上，在信噪比大于等于10 dB 时其检测性能略优于本文方法。

图3 5 种方法在不同信噪比下的检测准确率对比Fig.3 Comparison of the detection accuracy of five methods under different signal-to-noise ratios

5 结束语

GDE 准则及现有改进方法大多只能估计比阵列天线阵元个数少2 个的信源个数。为弥补这一缺陷，本文提出一种基于多重特征融合的信源个数估计方法，从WGDE 准则得到的增广加权盖尔圆盘矩阵中同时获取盖尔圆心、盖尔圆半径和加权盖尔圆半径等多重特征进行融合，构建可描述信源个数的特征向量，并利用SVM 训练分类器数学模型用于信源个数估计。基于4-UCA 的仿真结果表明，本文方法不仅能够准确估计仅比阵元数少1 的信源个数，而且在低信噪比和小快拍数条件下也具有良好的估计性能。本文未考虑信号源数目大于或等于阵元数目的情况，后续将从这一角度出发对信源估计方法做进一步探索。