基于数据驱动的人机混驾多车协同控制算法*

王会鲜 李 波 郑洪江 陈 伟

（1.上海立信会计金融学院信息管理学院 上海201209；2.上海智能网联车载终端工程技术研究中心技术部 上海200030；3.上海博泰悦臻电子设备制造有限公司技术部 上海200030；4.武汉理工大学自动化学院 武汉430070）

0 引 言

近年来，随着无人驾驶技术以及车车、车路通信技术的不断突破，对单车智能的研究逐渐转变为对车路协同系统[1]的研究。多车协同控制[2]由于具有以下3 个方面的优势而得到了学者的广泛研究：①在保证驾驶安全的前提下，通过控制车车间距达到最小化，有效的提高了道路的通行能力，缓解了交通拥堵[2]；②由于车车之间能够实时共享各自的状态信息，使得车辆具有更好的预测能力，从而提前做出准确的决策[3]，能够有效减少交通事故的发生；③车辆保持队列的行驶状态能减少实际交通环境中的“走走停停”现象[4-5]，从而有效的减少了燃油消耗[6]。在车联网环境下，车辆可以利用LTE-V2X通信获得周围车辆的BSM 数据以及与道路相关的MAP 信息，促进了车车之间以及车路之间实现高效的协同合作方式，有利于多车协同控制系统的实现。

自适应巡航控制（ACC）系统[7]作为高级辅助驾驶系统（ADAS）的1种，是最早用于实现多车协同控制的1种手段[7-8]。结合LET-V2X通信技术，ACC拓展为协同自适应巡航控制（CACC）系统[9]，具有更好预测能力。比如，由荷兰经济事务部资助的Connect &Drive 项目使用了6 辆乘用车进行了CACC 演示多车编队控制，该系统采用了恒定的时间间隔策略[10]。2016 年，无人车辆协同驾驶挑战赛（GCDC）举办第二届，旨在演示多车协同控制系统如何在接近真实交通场景的情况下执行复杂的操作，测试了2个平行车队的合并以及交叉路口场景，同时展示了C-ITS 如何帮助创建应急车辆的自由通行[11]。2018年，奥本大学利用2 辆Peterbilt 579 和2 辆M915 在美国移动中心及公共道路上进行了队列测试，测试结果表明，即使在交通非常拥挤的情况下，4辆卡车排也能够完成换道操作，并且系统也能保持车辆之间的恒定间距[12]。

然而目前对于CACC系统的研究主要是假设车队中除了leader 以外的所有车辆都为无人驾驶车辆，配备有传感器、控制器以及执行器。但在今后较长的一段时间中，有人驾驶车辆和无人驾驶车辆混行在道路上，如何处理人机混驾混合组成的多车协同控制值得深入研究。

从控制的角度看，目前大多数对多车协同控制系统的实现主要是基于线性二次型调节器（LQR）、模型预测控制（MPC）以及强化学习（RL）等方法。T.Stanger 等[13]采用LQR 方法优化由人机混驾组成的多车协同控制系统的控制增益，但是该方法需要准确的知道车队系统中与驾驶员驾驶行为习惯相关的参数以及与车辆系统动力学相关的参数。Cao Wenjing 等[14]设计了1 种线性MPC 作用于CACC 系统，与以前提出的模型预测控制方法相反，其目标是更高的燃油效率，它包含了对近似燃油消耗而不是加速度的直接惩罚。然而，基于MPC的方法通常依赖于1个先验系统模型，同时，该方法很难保证闭环系统的稳定性。C.Desjardins等[15]利用RL方法设计了CACC 系统中无人驾驶车辆的控制器，使用函数逼近技术和梯度下降学习算法作为直接修正控制策略的方法以优化其性能。然而，由于缺乏稳定性分析，可能导致传统的RL方法存在安全问题。

上述研究主要是基于自动网联汽车进行多车协同驾驶设计，需要准确获取多车系统中与驾驶员驾驶行为相关的参数以及与车辆系统动力学相关参数（这些参数在实际交通系统中无法准确获取），并且这些方法也很难满足复杂交通环境下的实时计算要求以及对无人驾驶车辆控制精度要求，不能解决实际情况下复杂交通环境的问题。

本文以人机混驾混合组成的多车协同控制场景为研究对象，设计了基于数据驱动的自适应动态规划横纵向控制算法。该控制策略仅仅利用多车系统中车辆的在线状态信息BSM 数据以及与道路相关的信息MAP数据（车辆的前轮转角以及车辆期望的纵向加速度）作为控制器的输入，利用能够保证动态系统稳定的递推数值方法在线逼近最优解，控制无人驾驶车辆在多车系统中保持期望的车速并且与前车保持期望的车间距，同时在任意曲率道路上行驶时与车道中心线之间的横向误差趋于0。

1 人机混驾多车协同场景数学模型构建

本文主要研究的是人机混驾多车协同控制场景，见图1。图1 中#1、#2 和#4 为有人驾驶车辆，#3和#5 为无人驾驶车辆。其数学模型包含了2 部分：无人驾驶车的横向控制模型和加入间距控制策略的纵向控制模型。前者确保了无人驾驶车辆能够在任意曲率道路上行驶时与车道中心线之间的横向误差趋于0，后者确保了无人驾驶车辆能够在队列系统中与前车保持期望的车间距。

本文中所使用的符号及其含义见表1。

图1 人机混驾组成的多车协同控制Fig.1 Multi-vehicle cooperative control consisting of manned and unmanned vehicles

表1 人机混驾多车协同控制机制符号Tab.1 Notations for the multi-vehicle cooperative control strategy

1.1 无人驾驶车横向控制数学模型

无人驾驶车辆横向误差的计算原理见图2。

根据图2中车辆当前的期望轨迹及实际轨迹信息可以得到无人驾驶车辆横向误差e1和航向误差e2的计算公式为

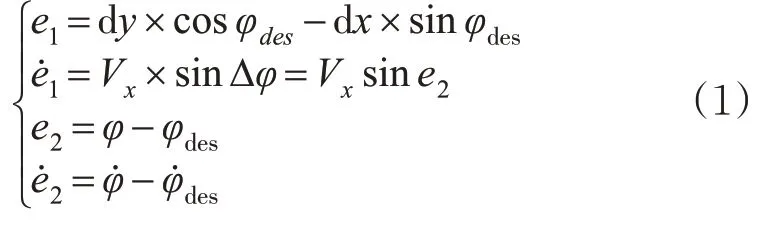
图2 横向误差计算原理示意图Fig.2 Calculation principle of the lateral and heading errors

式中：dx=x-xdes，dy=y-ydes；横摆角速度φ̇可以从本车BSM消息中获得；期望横摆角速度φ̇des可以结合本车BSM消息，以及和道路相关的MAP消息，利用公式̇des=Vx·ρ求解得到。

根据车辆运动学以及动力学[16]，无人驾驶车辆的横向方向盘控制模型可以写成如式（2）的系统状态方程

1.2 基于间距控制策略的纵向控制数学模型

假设图1中第i辆车的长度为li，xi表示第i辆车前保险杠所在的位置。因此，第i辆车和第i-1辆车之间的车间距hi可以表示为：hi=xi-1-xili，对时间t进行求导之后可以得到

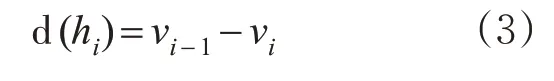
为了使有人驾驶车辆达到期望的运行速度，并且保持期望的车间距，需要在式（3）的基础上补1条跟车规则，即速度或者加速度必须作为激励函数给出。

因此，本文采用关于车间距hi、相对速度ḣi和本车速度vi的最优速度模型（OVM）[17]来模拟不同驾驶员的驾驶行为

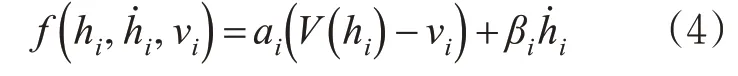
式中：ai和βi为与驾驶员驾驶行为习惯相关的参数。

对于函数V(·) ，需要满足：①连续且单调递增的，因为交通越稀疏，驾驶员倾向于以越快的速度行驶；②当本车与前车的间距h≤hstop时，V(h)≡0，因为在交通非常拥堵的情况下，驾驶员倾向于停车；③当本车与前车的间距非常大时，V(h)≡vmax。故最优相对速度函数可表示为

对最优相对速度函数V(·) 在期望状态点(h*，v*)进行泰勒展开，可以把非线性模型线性化，得到有人驾驶车辆的系统状态方程

同理，对于无人驾驶车辆#3 和#5，采用车头时距控制策略[18]，定义车头间距为：hi，des=τivi+hi*，其中，hi*为制动距离，τi表示最小的车头时距，因此第i辆无人驾驶车辆实际的车头间距与期望的车头间距之间的误差可以表示为Δhi=hi-τivi-hi*。则无人驾驶车辆的系统状态方程用误差量可以表示为

2 数据驱动的自适应动态规划控制算法

在人机混驾混合组成的多车协同控制场景中，由于车辆行驶时不可避免地存在某种干扰的影响，导致车队中车辆行驶状态总是会发生偏离，很难时时保持在期望状态。为使偏移车辆能及时回归到期望状态，本文采用自适应动态规划控制算法对无人驾驶车辆行进轨迹进行实时控制。

对于无人驾驶车辆控制机制的设计包含2个部分：横向控制机制设计和纵向控制机制设计。

对于横向控制机制，主要控制目标为：①为了使车辆按照期望的轨迹行驶，横向误差以及航向误差需要保持尽可能小；②在发生横向操作时，为了获得更好的乘客舒适性，控制输入即方向盘转角不应该过大。考虑以上2个因素，控制目标为找到1个线性控制器

来最小化下列性能指标

纵向控制机制是为了使车辆达到期望的车速，并且与前车保持期望的车间距，因此控制目标包括：①速度误差vi-v*及车头间距误差hi-h*应该尽可能小；②在实际的交通环境中，考虑到交通安全以及交通吞吐量，期望的车速以及车间距不应该过大也不应该过小；③多车协同控制的1 个目的是为了降低燃油消耗，因此，控制输入u 应该保持较小值。

考虑以上3个因素，与横向控制机制类似，控制目标为1个线性控制器

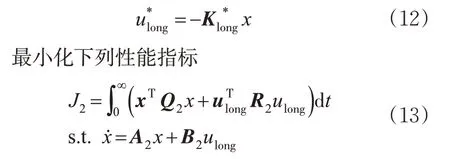
由于横向和纵向控制机制具有相同的表达式，只是具有不同的状态矢量X、与状态量相关的权重矩阵Q、与控制量相关的权重矩阵R 以及与系统矩阵A 和B 。因此，接下来对控制算法的推导将不再区分二者。

将式（2）和式（9）表示的连续时间系统离散化后可以得到

式中：P*=P*T＞0 为下列代数黎卡提方程（ARE）的最优解

但是，上面的算法需要准确的知道系统矩阵As和Bs。在横向控制机制中，As和Bs中包含了与系统动力学相关的参数，而在纵向控制机制中，As和Bs包含了与驾驶员驾驶行为习惯相关的参数，这些参数在实际的交通环境下是无法准确获取的。

因此，本文通过对最优反馈控制矩阵K*进行优化求解，提出基于数据驱动的自适应动态规划控制算法（见图3），可以简化系统的控制输入参数，利用V2X 通信获得的实时数据作为控制输入，来实现无人驾驶车辆的优化控制。

该算法在传统自适应动态规划控制算法[17,19]的基础上进行优化。令Aj=As-BsKj，可将系统状态方程式（14）改写为

根据文献[17]中递归求解李雅普诺夫方程的算法，同时结合式（18）和式（19）可以得到

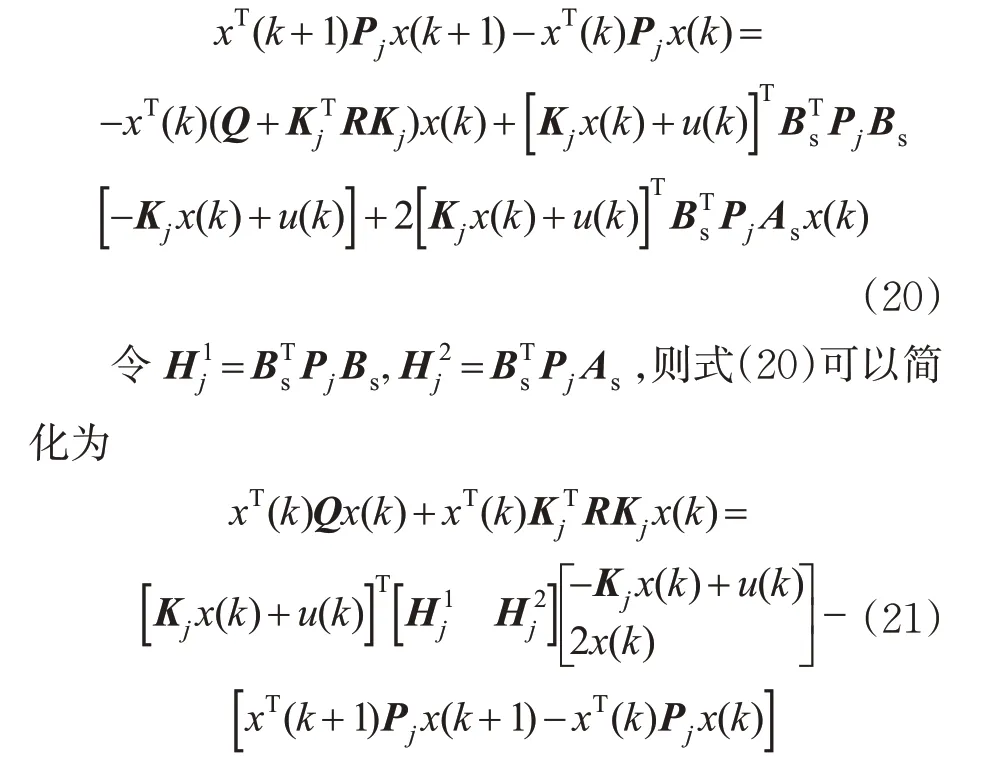
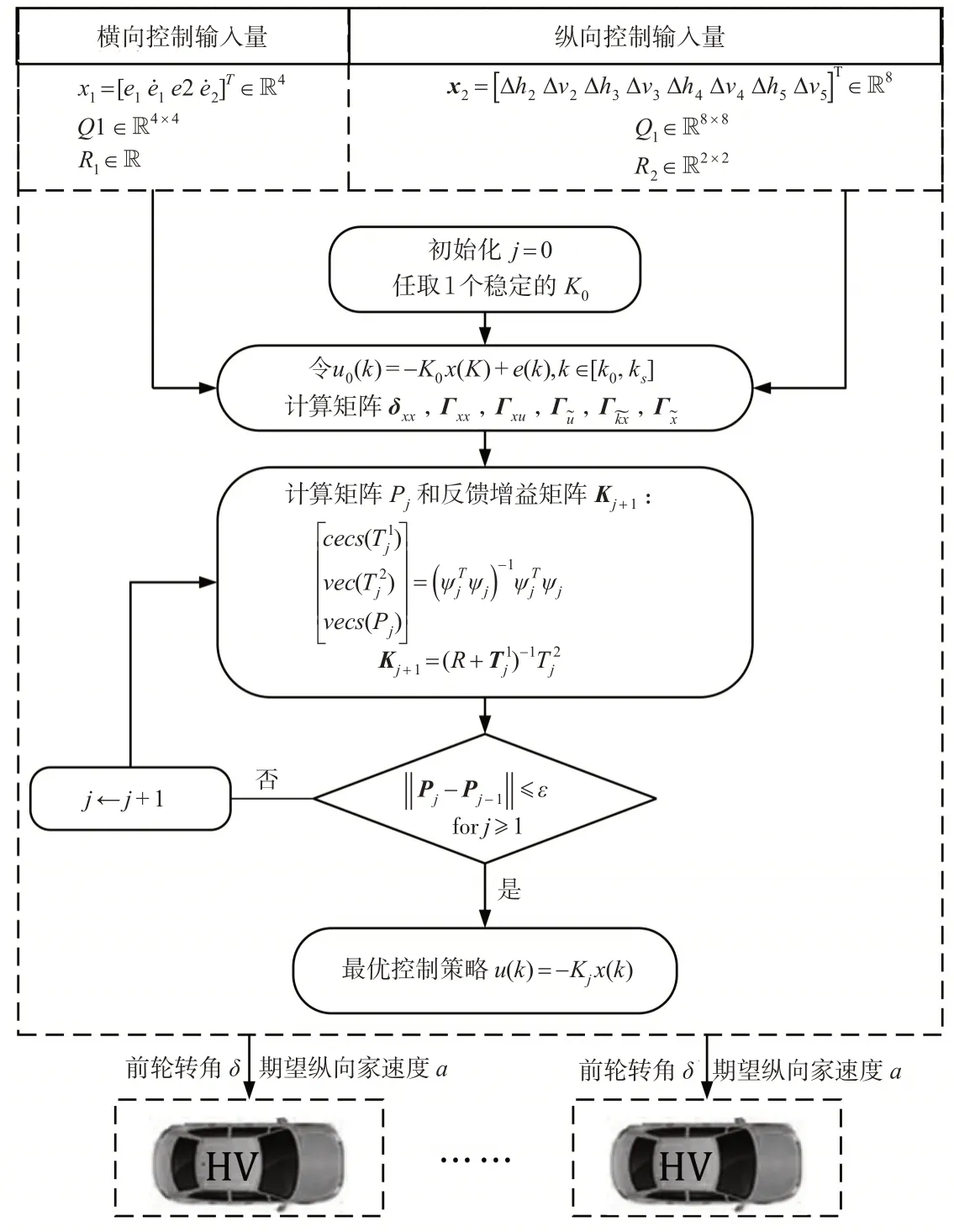
图3 数据驱动的自适应动态规划控制算法Fig.3 Data-driven adaptive dynamic programming-control algorithm

如果矩阵ψj是列满秩的，则式（22）可以利用下式进行求解。

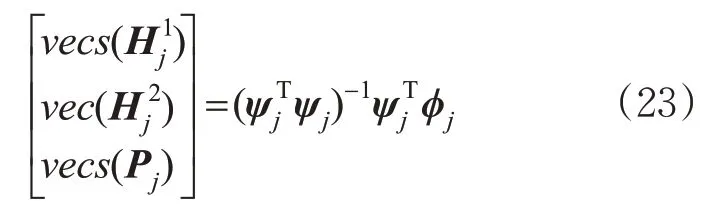
反馈增益矩阵Kj+1可以利用下式迭代求解。

可知，基于数据驱动的自适应动态规划控制算法仅仅利用V2X通信获得的在线数据：车辆的前轮转角δ以及车辆期望的纵向加速度a，作为控制输入，即可实现无人驾驶车辆的优化控制。

3 仿真实验与结果分析

为了说明本文设计的基于数据驱动的自适应动态规划控制算法能够有效的实现由人机混驾车辆组成的多车协同控制系统中无人驾驶车辆的横纵向控制，本文基于CarSim和Simulink进行联合仿真测试验证，分析所设计的横纵向控制机制控制效果以及收敛速度。

3.1 单无人驾驶车横向控制仿真分析

为了说明横向控制器的控制效果以及适应性，本文考虑了道路曲率连续发生变化的螺旋型道路以及S 型道路，分析无人驾驶车辆在数据驱动的自适应动态规划横向控制算法作用下能否有效的逼近期望轨迹，并且始终保持稳定的控制状态。

首先在CarSim 中设置1 条螺旋形式的曲线道路，设置车辆的纵向速度Vx=10 m/s，同时还考虑了初始时刻，车辆具有1个横向偏移量为1 m，即把车辆的初始位置设置在距离车道中心线1 m 的地方。为了实现仿真，需要对控制算法中的某些参数进行初始化，在本文中设置状态量的权重矩阵Q=diag {0.01，0.01，0，0} ，控制量的权重矩阵R=diag{1} 。最后，对矩阵P达到收敛时的标准进行设置，在本文中假设当时，迭代停止，最优反馈控制达到最优K*。得到仿真结果见图4。

图4 螺旋型道路下的无人驾驶车横向控制仿真结果Fig.4 Simulation results of the lateral control of autonomous vehicles on spiral roads

根据图4（a）可以看出车辆有1个初始的横向偏移量1 m，然后在大概1 s的时间内横向误差稍微有所增大，主要原因是在这段时间内，控制器收集本车的状态数据以及与道路相关的数据来求解最优的控制器K*，因此控制器相当于没有输出作用于车辆，所以在前1 s的时间内车辆的前轮转角为0，见图4（b）。但是由于道路具有曲率，所以无人驾驶车辆在这段时间内的横向误差稍微有所增加。由于开始的横向误差较大，为了使车辆横向误差最终能够趋于0，当求解得到最优的控制器之后，会输出1 个较大的前轮转角作用于车辆，见图4（b）。当横向误差趋于0时，前轮转角随时间呈线性增加，这主要是由于螺旋线的曲率也是线性增加的，所以为了使横向误差趋于稳定状态，方向盘转角必须也要逐渐增加，见图4（c）。图4（d）则更加形象的展示了车辆的行驶轨迹为1条曲率不断增加的螺旋线。

从上述仿真结果可以看出，对于道路曲率连续发生变化且具有较大初始偏移量的情况，基于数据驱动的自适应动态规划横向控制算法能够很好的求解最优控制器，确保车辆与期望行驶轨迹之间的横向误差趋于0，且收敛速度较快。

对S型道路的工况进行仿真分析，其结果见图5。从仿真结果可以看出，控制器的收敛速度非常快，当初始横向误差为1 m时，在最优控制器的作用下，无人驾驶车辆的横向误差很快能够趋于0。从5（a）中还可以看出，在t=20 s 和t=40 s，横向误差会有1个较小的波动，主要是由于道路曲率的突变导致的，见图5（c），但最终被控车辆还是能够稳定下来。

图5 S型道路下的无人驾驶车横向控制仿真结果Fig.5 Simulation results of the lateral control of autonomous vehicles on S-Roads

综合螺旋型道路以及S形道路的仿真结果可以看出，在数据驱动的自适应动态规划横向控制算法作用下，控制器的收敛速度较快，控制效果非常好，适应性非常强，能够保证无人驾驶车辆在任意曲率道路上行驶时与道路中心线之间的横向误差能够始终趋于0。

3.2 人机混驾多车协同控制机制横纵向综合控制仿真分析

接下来验证人机混驾组成的多车协同控制场景中，在数据驱动的自适应动态规划横纵向综合控制算法作用下，无人驾驶车辆能否保持与道路中心线横向误差趋于0，同时在队列系统中达到期望的行驶速度并且与前车保持期望的车间距。

首先，在CarSim 中对道路场景进行搭建，见图6。在本场景中，主要可以分为3个阶段：0～400 m内是直线道路，＞400～600 m内为S形道路，最后再连接1条直线道路。接着，在Simulink中对无人驾驶车辆#3 和#5 的控制器进行搭建。然后，在CarSim 对有人驾驶车辆和无人驾驶车辆的初始速度以及在所设置道路上的初始位置进行设置。同时控制算法中需要对车辆的最大车速、制动距离等参数进行设置，所有的初始化参数见表2。

图6 人机混驾多车协同控制系统行驶轨迹Fig.6 Trajectory of the multi-vehicle cooperative-control system

表2 人机混驾多车协同控制系统初始化参数设置Tab.2 Initialization parameters of the multi-vehicle cooperative-control system

从表1 可以看出，第3 辆无人驾驶车辆的制动距离设置为9 m，同时最小车头时距设置为1 s，由于在第1 条直线道路上所有车辆的期望速度为15.56 m/s，因此，当第3 辆无人驾驶车辆达到期望速度时，其与前车的期望车头间距为h3，des=τ3v3+h*3，代入数值为24.56 m，与第1 和第2 辆车之间的车头间距保持一致；当驶离弯道进入第2 条直线道路后，车辆的期望速度为20 m/s，当第3辆无人驾驶车辆达到此速度时，其与前车的期望车头间距为29 m，同样与有人驾驶车辆之间的车头间距保持一致。同理，也可以计算出在第1条直线道路和第2条直线道路上第5辆无人驾驶车的期望车头间距。最后得到人机混驾组成的多车协同控制系统在数据驱动的自适应动态规划横纵向综合控制算法作用下车速和车间距随时间的变化曲线见图7。

图7 人机混驾车辆车速和车间距随时间的变化关系Fig.7 Trajectory of the velocity and headway under the lateral and longitudinal integrated control scene

由图7 可见，无人驾驶车#3 以=8 m/s 的初始速度行驶，在t=1 s控制器更新，输出最优的控制量即期望的油门开度或制动踏板的力度作用于无人驾驶车辆，驱动其加速至期望的车速，并保持该速度行驶，同时与有人驾驶车辆#2之间的车间距达到期望车间距=24.56 m。无人驾驶车#5 以=4 m/s初始速度行驶，由于第5辆车需要收集前面4辆车的状态数据，因此其状态量的维度更大，在采样时间相同的情况下，其需要收集更长时间的数据，才能达到满秩的条件。控制器在t=3 s 左右更新，控制器输出最优的控制量作用于车辆，使其加速至期望车速，并且当车速达到时，其与有人驾驶车辆#4 之间的车间距达到期望车间距=24.56 m。多车协同控制系统大约在时间t=20 s时驶入弯道，大约在时间t=40 s时驶离弯道。当驶离弯道后进入第2段直线道路，此时参考车辆开始加速，最后达到新的期望车速=20 m/s，因此当其后面的4辆车驶离弯道后也跟随头车加速至。最后，5 辆车又达到相同的车速，并且保持相同的车间距=29 m。综合上述分析可以看出，对于2辆无人驾驶车#3和#5，利用数据驱动的自适应动态规划控制策略能够使车辆控制器很快收敛，达到期望的运行状态，并且在整个过程当中稳定性都非常好。

为了分析多车协同控制系统进入曲线道路时数据驱动的自适应动态规划控制算法对无人驾驶车辆的控制效果，还做出了车辆与车道中心线之间的横向误差大小以及横摆角随时间的变化曲线见图8。

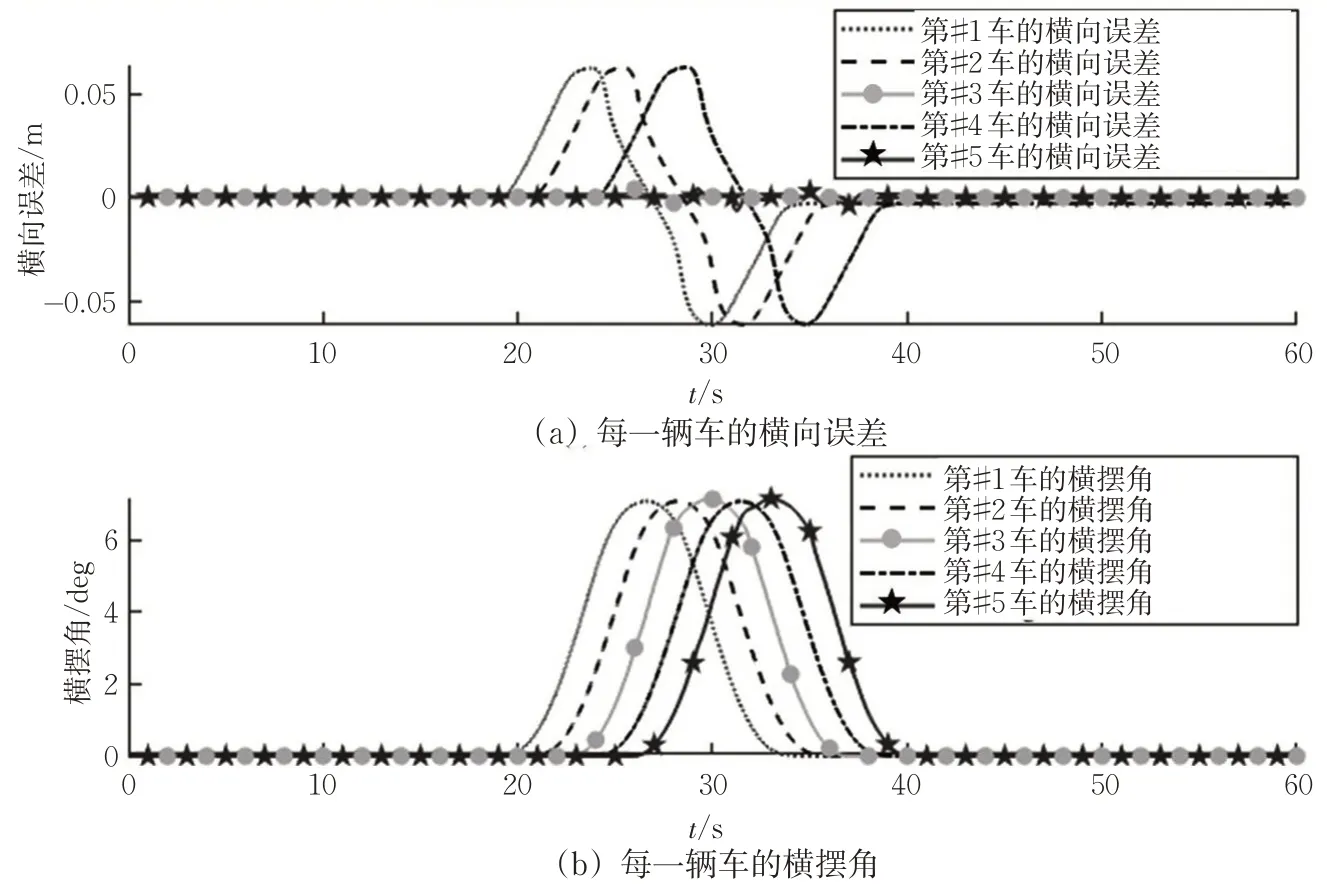
图8 车辆横向误差和横摆角随时间的变化关系Fig.8 Trajectory of the lateral error and yaw angle under the lateral and longitudinal integrated control scene

由图8（a）可见，对于有人驾驶车辆#1、#2和#4，由于使用的是CarSim自带的控制器，其控制原理较为简单，因此在弯道行驶的过程当中，其横向偏差较大，而对于无人驾驶车辆#3 和#5，其横向偏差基本接近于0，从而说明了基于数据驱动的自适应动态规划控制策略对于在弯道上行驶的车辆也有非常好的控制效果。

综上所述，可以得到在由直道和S 形道路构建的复杂场景下，基于数据驱动的自适应动态规划策略不仅在直线道路上有很好的控制效果，在曲率大小和方向变化的弯道行驶时也有不错的控制效果，即在该控制策略的作用下，无人驾驶车辆能够达到期望的运行速度以及与前车保持期望的车间距，同时与车道中心线之间的横向偏差也趋于0，并且在整个行驶的过程中都保持稳定的状态。

4 结束语

本文以人机混驾组成的多车协同控制场景为研究对象，提出了基于数据驱动的自适应动态规划控制算法。通过对多车系统的横纵向控制机制分别进行分析，推导出系统的状态方程，采用递推数值方法在线逼近最优解，并通过对最优反馈控制矩阵进行优化求解，简化了系统的控制输入参数。基于CarSim和Simulink 进行联合仿真测试验证，分析所设计的横纵向控制机制控制效果以及收敛速度，得出如下结论。

1）简化了控制输入参数，仅仅利用V2X 通信实时获得的车辆的前轮转角以及车辆期望的纵向加速度数据作为控制输入，即可实现人机混驾多车协同控制。

2）对于道路曲率连续发生变化且具有较大初始偏移量的情况，该控制算法能够很好的求解最优控制器，确保车辆与期望行驶轨迹之间的横向误差趋于0，且收敛速度较快。

3）在由直道和S形道路构建的复杂场景下，该控制算法不仅在直线道路上有很好的控制效果，在曲率大小和方向变化的弯道行驶时也有不错的控制效果，即在该控制策略的作用下，无人驾驶车辆能够达到期望的运行速度以及与前车保持期望的车间距，同时与车道中心线之间的横向偏差也趋于0，并且在整个行驶的过程中都保持稳定的状态。