散射项约束非负矩阵分解的高光谱图像解混

陈善学，董桓宇，陈雯雯

(1.重庆邮电大学 通信与信息工程学院,重庆 400065；2.重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)

0 引 言

高光谱图像具有较高的空间分辨率与丰富的光谱信息的特点使其在多个领域有着卓越的表现，例如在军事、环境、海洋、地理、农业等领域，高光谱遥感技术都发挥着重要的作用，因此，高光谱技术的研究在国防、生产、生活中显得极为重要。尤其高光谱图像解混技术，其对地物成分和光谱特性的体现，使其成为高光谱技术研究的新秀和宠儿，成为高光谱遥感技术研究最为重要的内容之一。

由于高光谱图像具有丰富的光谱信息和空间特征，使得解混方法蓬勃发展。端元提取算法主要有纯像元指数法(pixel purity index, PPI)[1]，最大体积法N-Finder[2]，顶点成分分析(vertex component analysis, VCA)[3]，正交基算法(orthogonal bases algorithm, OBA)[4]，曲线成分分析(curvilinear component analysis, CCA)[5]等，丰度估计较常用的算法是全约束最小二乘法(fully constrained least squares, FCLS)[6-7]。

文献[8]和文献[9]分别详细地总结了国内外基于线性模型和非线性模型的高光谱图像解混的研究情况，并针对近几年的研究成果提出了问题与展望。约束非负矩阵分解是高光谱解混算法中的一个热点：文献[10]提出最小体积约束非负矩阵分解(minimum volume constrained nonnegative matrix factorization,MVC-NMF),用最小体积项(minimum volume term)作为目标函数的约束条件，构成新的目标函数，这一算法被后来的一些研究人员进一步研究改进[11-12]。文献[13-14]进行了关于L1/2稀疏性约束非负矩阵分解(L1/2-NMF)和平滑性约束非负矩阵分解(smoothness constraint nonnegative matrix factorization, CNMF)的研究。近年来国内外越来越多的研究人员关注于约束非负矩阵分解的算法研究。文献[15]提出一种了基于神经网络的稀疏性约束非负矩阵分解方法：L1-DNMF算法。文献[16]也研究了结合深度学习的总体差值稀疏性约束非负矩阵分解(sparsity-constrained deep nonnegative matrix factorization with total variation, SDNMF-TV)的方法。文献[17]提出基于非线性模型，对L1/2稀疏性约束和平滑性约束的结合方法，用核方法进行优化的算法，即基于丰度约束核非负矩阵分解的非线性光谱解混算法(abundance sparseness and smoothness constrained KNMF, ASSKNMF)。文献[18]通过结合Euclidean范数稀疏约束和Frobenius范数稀疏约束的方法，提出了一种强鲁棒性约束非负矩阵分解的解混方法。还有其他许多关于约束非负矩阵分解的解混方法，这里就不做介绍了。

以上介绍的关于约束非负矩阵分解的解混算法，都有着明确的数学意义和一定程度上的物理意义，并在真实数据的实验中，有着优秀性能。但是这些方法或基于图像的马卡洛夫模型的随机特性，或基于数据的稀疏特性，亦或是基于数据的空间连续性、平滑性，都是考虑到数据的数学特性，而在真实场景的物理背景上考虑的程度较为有限。STC-NMF算法在前人的线性模型上进行约束非负矩阵分解算法研究的基础上，受Hapke辐射传输理论[19]的启发。根据辐射传输理论，在大气的辐射传输中，大气中存在的胶着物和悬浮物对光线的辐射传输有着不可忽视的作用。由大气中的微粒，如烟、尘埃、小水滴及气溶胶等会引起形成近似夫琅禾费衍射现象，其方向性比较明确。表现在传感信号上，由接收仪器接收，就会形成在本像素点的射入射出信号，即被邻域的散射信号干扰，同时又干扰邻域信号，因此，STC-NMF算法对物理层面有较多的考虑，这是不同于以往算法的。这一算法在目标函数中，将干扰看作噪声和具有现实物理意义的散射，并以散射项作为约束项参与约束算法。也正是因为如此，STC-NMF算法虽然还存在着许多不足，但在实验中仍旧具有非常优秀的解混性能。此外，由于约束项在数学形式与数学特性上与一些较为知名且被较多引用的算法，如CNMF，L-SNMF，SDNMF-TV等都具有较高的相似性，所以，STC-NMF算法在实验仿真中也有着不错的表现。

1 相关工作

1.1 线性混合模型

线性混合模型(linear mixing model, LMM)是一种重要的混合模型，具有简单明了的数学特性和一定的物理意义，在高光谱解混领域拥有举足轻重的地位，很多研究都建立在线性混合模型之上。在一般情况下，像元的反射率可以近似地看作端元的线性混合

R=AS+n

(1)

(1)式中：R为像元反射率；A为端元反射率矩阵；S为丰度矩阵，地物丰度满足非负性与全加性；n为噪声干扰。

1.2 非负矩阵分解

在线性解混模型中，将像元的反射率看作端元丰度线性组合，若在理想条件下，符合公式(1)，各种各样的影响因素都可看作噪声，那么有

n=R-AS

(2)

若使得‖n‖最小，采用文献[20]提出的非负矩阵分解。构建目标函数为

(3)

则求min‖n‖的问题将等同于求arg minf(A,S)问题，根据梯度下降算法，其乘法迭代规则为

A←A.*(RST)./(ASST)

(4)

S←S.*(ATR)./(ATAS)

(5)

每个符号代表的意义同公式(1)，.*和./分别代表矩阵的点乘和点除。

2 散射项约束非负矩阵分解

散射相函数即为介质相位函数，在辐射传输理论中常用以描述米氏散射(Mie scattering)，是对于处于均匀介质的各向同性的单个介质球在单色光照射下，基于麦克斯韦方程边界条件下的严格数学解。其中最简单最常用的是Henyey-greenstein项函数

(6)

但由于Henyey-greenstein项函数的形式较为复杂，因此本文选用相对简明的，在文献[19]中提出的勒让德多项式形式的散射相函数。在文献[19]中，Hapke提出勒让德多项式形式的散射相函数为

P(g)=1+bcosg+c(3cos2g-1)/2

(7)

本文采取将勒让德多项式形式的散射相函数作为目标函数中的约束条件对图像进行解混，目标函数变化为

(8)

(8)式中：λ定义下降速度；g是非对称因子；b与c是可调节参数。由于入射波的相位在粒子上是不均匀的，造成了各子波在空间和时间上的相位差，因此，本文用地物在像素点的丰度与其四邻域相同地物的丰度的平均值求差，将差值的绝对值作为非对称因子描述由于大气散射造成不同像素空间中相同地物间的散射项贡献，则定义非对称因子g为

(9)

(9)式中：Spk为k地物在p像素点的丰度；SNpk为这一地物在该像素点四邻域丰度均值；p是像素点的四邻域。〈〉表示矩阵元素的和为

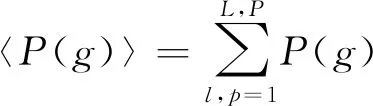
(10)

将散射项约束作为约束条件，其物理意义为，将干扰因素看成2部分组成，分别是噪声和邻近区域米氏散射影响，并将米氏散射对邻域贡献看成是线性的。以丰度差值作为非对称因子，在宏观上以单个像元所处空间作为单位，以此计算像素总体相位差异，求相同地物在邻域具有不同空间占有率情况下，因米氏散射对该像元区域造成的贡献。在数学上，文献[14]采用MRF模型，将平滑性约束作为约束项，以此达到对数据进行分段平滑性约束的目的。平滑性约束为

g(x)=-e-x2/γ+1

(11)

将约束项泰勒展开为麦克劳林级数有

(12)

而散射项约束项展开为

(13)

(13)式中，o(x),o(g),o(2g)为二阶余项。在形式上g(x)与p(g)二阶泰勒展开式相似，如果继续展开到高阶依旧相似，且对丰度约束而言，x和g的定义域相同，说明两者有着相近的数学意义，即勒让德多项式形式的散射项函数作为约束项也具有一定程度的分段平滑性约束的能力。由于相近的数学意义，则其梯度下降算法的新乘法迭代规则也可借鉴文献[14,20-21]确定，即

A←A.*(RST)./(ASST)

(14)

S←S.*(ATR)./(ATAS+λS.*

[-bsinΨ-3ccosΨsinΨ]

(15)

(15)式中，矩阵Ψ为像素点位置对应的非对称因子g所组成的矩阵。

证明借鉴文献[14,20]，定义有辅助函数G(S,St)使得

St+1=arg minG(S,St)

(16)

(16)式中：上标t表示当前状态；t+1表示下一状态，满足迭代要求的关系

F(St+1)≤G(St+1,St)≤G(St,St)=F(St)

(17)

不妨假设辅助函数为

G(S,St)=F(St)+(S-St)T(∇F(St))+

(18)

(18)式中：

K(St)=diag((ATASt)./St)+λP′(Ψ)

(19)

那么对比目标函数为

F(S)=F(St)+(S-St)T∇F(St)+

(20)

根据(20)式，有G(S,St)≥F(h)，即为

(S-St)T(ATA-K(ht))(S-St)≥0

(21)

可以推出∇SG(S,St)趋向于零

(22)

通过化简与简化，关于丰度矩阵的乘法迭代规则可以确定为

(23)

STC-NMF算法如下。

输入：高光谱图像R，像素点数P，I行J列，波段数L;

步骤1：使用N-Finder或Hysime初始化端元矩阵A，然后用Fcls初始化丰度矩阵S;

步骤2：使用公式(14)更新端元矩阵A;

步骤3：使用公式(12)更新丰度矩阵S;

步骤4：一直重复步骤2，步骤3更新，直到达到最大迭代次数，或目标函数，即公式(8)满足fnew(A,S)-fold(A,S)

输出：端元矩阵A与丰度矩阵S.

3 实验与讨论

3.1 数据集

本文使用的数据集是用由朱飞云博士整理并在科研在线公开的数据，与文献[14]相同，数据是美国地质调查局的urban场景，307×307像素的数据区域，去除1-4, 76, 87, 101-111, 136-153和 198-210波段的162个波段。图1为该场景第9个波段的成像图。

图1 Urban场景第9个波段的成像图Fig.1 9th band image of urban

3.2 参数设置与算法对比

仿真实验在主频3.7 GHz，内存8 GB的PC机上进行，操作系统为Window(64位)，仿真平台为Matlab2014a(64位)。散射项约束非负矩阵分解中有3个参数λ,b,c可以设定,其中,λ调节乘法迭代规则的梯度下降速度，b,c作为调节参数，可根据对数据的适应性做调整，根据(12),(13)式，这2个参数满足特定条件时，可以看做进行平滑性约束的塑形参数。这里将这3个参数依次设置为0.01,0.2和0.1进行实验。实验L1/2-NMF算法设置调节参数λ为0.01，CNM算法设置调节参数λ为0.01，γ为0.01。实验结果，评价指标最优结果用下横线标出。关于实验结果的评价标准有：光谱信息散度(special information divergence, SID)，均方根误差(root mean square error, RMSE)。本次实验与还原的L1/2-NMF算法、CNMF算法以及VCA+FCLS算法进行对比，实验结果如表1和表2。

表1 Urban场景的4端元光谱信息散度

表2 Urban场景的4端元均方根误差

以上端元对比，通过对比可以得到，在上述实验条件下，与L1/2-NMF和CNMF相比较，STC-NMF算法性能有一定的提升，同时这3种算法相比较VCA+FCLS都有较为明显的提升，虽然VCA+FCLS在沥青路和屋顶2个端元解混效果也不错，但相比较其他算法并没有明显优势，所以暂时不做过多讨论。在表1、表2的具体数值比较，STC-NMF算法解混的4种地物端元都拥有着优秀的性能，但与L1/2-NMF和CNMF相比较并没有特别明显的优势。从端元的波形图来看，这3种算法解混出来的波形与真实地物的波形都很接近，且大致轮廓基本一致，其中STC-NMF算法计算出来的端元与真实端元最为接近；但是这3种算法在关于屋顶的端元解混，效果都不太好，有较为明显的差异，但其中STC-NMF算法仍优于另外2种算法解混出来的，在波形上与真实地物也更为贴合。

图2 4种算法与真实端元的端元对比Fig.2 Endmembers comparison with real endmembers of the four algorithms

图3 真实地物四端元丰度图Fig.3 Abundance for 4 endmembers of ground truth

图4 STC-NMF算法四端元丰度图Fig.4 Abundance for 4 endmembers of STC-NMF

图5 L1/2-NMF算法四端元丰度图Fig.5 Abundance for 4 endmembers of L1/2-NMF

图6 CNMF算法四端元丰度图Fig.6 Abundance for 4 endmembers of CNMF

图7 VCA算法四端元丰度图Fig.7 Abundance for 4 endmembers of VCA

从丰度图直观的视觉感受来看，3种算法皆明显优于VCA，因此，在此处也暂时对VCA不做过多讨论。STC-NMF对于沥青路的解混效果略优于CNMF，但略差于L1/2-NMF；对草地的解混效果3种算法无明显的感觉差异；对于树木的解混效果STC-NMF略优于另2种算法；对于屋顶的解混效果没有造成感官上的明显优势，3种算法都有将沥青路出现在屋顶的地物丰度之中，但相比之下，在图像左部区域，STC-NMF树木与屋顶的丰度差异较为明显一些，也相比之下略微贴近真实地物的丰度图。

特别需要注意的是，不论在端元对比亦或是丰度对比，关于屋顶的解混效果，VCA略优于这3种算法，这是优于为了对比更加公正、更加明显，实验中STC-NMF，CNMF，L1/2-NMF 3种算法初始化，都是用N-Finder初始化端元，用FCLS初始化丰度；而VCA本身作为聚类方法可以为算法进行端元初始化。在实验中经过多次对比，此场景的四端元解混中，进行屋顶端元解混，大约在第50个波段开始N-Finder初始化端元开始有较为明显的向上趋势，而VCA接近于真实地物，有向下趋势；而经过约束非负矩阵分解的梯度下降，有效抑制了这种向上的趋势，特别是STC-NMF最为有效，最为接近真实地物，但这种差异是由于初始化算法造成的，因此，STC-NMF也明显受到初始化算法聚类效果的影响。而实验中初始化选择N-Finder而不是VCA是因为在实验中，对于端元的初始化效果，不论是四端元或五端元亦或是六端元，N-Finder总体是优于VCA的，同时也是为了减小初始化对算法的影响。

4 结束语

本文提出一种将米氏散射看作干扰的约束非负矩阵分解算法，散射项约束非负矩阵分解，并将其与几种较为知名且被较多引用的算法进行对比。通过实验比较可以看出，这种算法在本组实验的既定条件下，性能要略微具有优势，即是说，还可以通过对调节参数的深入研究进一步使解混能力变优。而这种算法从理论角度出发，STC-NMF将约束项由抽象的数学符号到具象的物理意义，在梯度下降过程中，使得所求的端元与丰度更贴近于现实的情况，且其勒让德函数形式的数学解使得其在数学角度，与统计性、稀疏性等基于数学特性的约束也高度耦合，因此，STC-NMF应具有优秀的解混性能。通过实验仿真，可以证明，STC-NMF也确实有着不错的解混性能，相较于L1/2-NMF和CNMF，解混性能也具有一定的优势。