礁面大糙率存在下孤立波传播变形及爬高实验研究

杨笑笑，姚宇,2*，郭辉群，贾美军

(1.长沙理工大学 水利工程学院，湖南 长沙 410114；2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114)

1 引言

海啸是一种极具破坏性的自然灾害，它可以由海底地震、海底滑坡、火山爆发或陨石撞击产生，主要发生在沿海地区，其蕴含的巨大能量对海岸建筑物和人身安全构成了严重的威胁[1]。这种毁灭性的灾害在2004 年印度洋海啸和2011 年东日本海啸中均有报道[2-3]。近年来生物海岸（如红树林、珊瑚礁等）对海啸波的积极防御作用引起了从事灾后调查的学者们的广泛关注[4]。理想的珊瑚礁地形主要由连接深海海床较陡的礁前斜坡和延伸至海岸且水深较浅的水平礁坪组成[5]。在礁前斜坡、礁冠和外侧礁坪上常常有充分发育的珊瑚群落，造成地形地貌结构复杂多变和礁面粗糙度大且不均匀[6]。波浪向岸线传播过程中，由于礁缘处的破碎和礁坪上的摩擦损耗将削弱大量的入射波能，因此研究海啸波在珊瑚礁海岸附近的传播变形和岸滩爬高特征，可为评估珊瑚礁地形对海啸灾害的防治作用提供参考依据。

由于海啸波的首波接近孤立波，因此学术界多采用孤立波来模拟海啸波[7]。与对规则波和不规则波的研究相比，国内外利用物理模型实验来研究孤立波与粗糙珊瑚礁地形相互作用问题较为少见。文献中仅有Quiroga 和Cheung[8]将礁面糙率概化为与水槽等宽并按照一定间距分布的矩形木条，通过物理模型实验对不同礁面粗糙度时孤立波传播变形特性进行了研究。Yao 等[9]在物理模型实验中采用在礁冠附近均匀布置PVC 圆柱体来模拟粗糙的珊瑚礁面，研究了入射波高、礁坪水深、糙率以及潟湖宽度对孤立波传播变形与爬高的影响。但是Quiroga 和Cheung[8]的研究中由于采用了间距较大的人工木条糙率，并不能真实地代表实际珊瑚礁群落的情况。Yao 等[9]使用的圆柱体阵列虽能更真实地模拟鹿角类珊瑚群落，但是其糙率仅仅设置在了珊瑚礁缘破碎带附近。因此本文拟改进Yao 等[9]的实验设计，将整个礁体均设置人工糙率来进一步探讨粗糙礁面存在下孤立波传播变形及爬高规律。

2 物理模型实验设置

本研究的物理模型实验在长沙理工大学水利实验中心的波浪水槽中进行，水槽长40 m，宽0.50 m，高0.8 m。实验布置如图1a 所示，在水槽的一端设置一台推板式造波机。基于Becker 等[10]的野外观测，根据弗汝德相似准则构建了几何比尺为1∶20的珊瑚岸礁概化模型。整个珊瑚礁模型由厚度为1 cm的PVC 板构成（图1b），其中1∶6 的礁前斜坡设置距造波机27.3 m 处，随后连接长度为8 m 的水平礁坪并延伸至1∶8 的礁后岸滩斜坡，礁坪距水槽底部垂直距离为0.35 m。珊瑚岸礁模型通过悬挂在水槽边壁上的不锈钢杆固定，礁体模型宽度与水槽的宽度一致。

实验设置了18 个（G1−G18）电容式浪高仪测量自由液面高程的变化，采样频率为100 Hz，在礁缘的波浪破碎带附近浪高仪的布置相对密集。在礁后岸滩上绘制了间隔为1 cm 的标记线以测量波浪的爬高，同时采用1 个CCD 高速相机记录孤立波的爬坡过程。

本实验拟参考Yao 等[9]采用的圆柱体阵列来人工模拟生长有鹿角类珊瑚的珊瑚礁面。在整个礁前斜坡和礁坪区域内均匀布置由直径为d=1 cm、高度为3.5 cm 的木质材料制成的圆柱体阵列（图1c），相邻柱体间距为S=2.5 cm（图1d）。圆柱体粗糙单元固定于礁面PVC 板预留的孔洞中，洞深1 cm，故礁坪上人工糙率的高度为2.5 cm。柱体的密度采用固体体积分数φ=Vs/V进行计算，式中V为控制体体积，Vs为控制体中圆柱体所占体积，对于本实验设置 φ值为0.126。

基于光滑（φ=0）和粗糙（φ=0.126）两种礁面，本实验分别测试了5 种入射波高（H0=0.04 m,0.06 m,0.08 m,0.10 m 和0.12 m）和4 种礁坪水深（hr=0.025 m,0.05 m,0.075 m 和0.10 m）共计40 种组合工况，根据前述的相似准则和几何比尺（1∶20），对应的原型波浪要素为H0=0.8～2.4 m 和hr=0.5～2 m。

3 结果分析

3.1 孤立波垂直于岸线方向沿礁的传播变形过程

图2 以入射波高H0=0.08 m 和礁坪水深hr=0.08 m的典型工况为例，展示了孤立波分别与光滑礁面和粗糙礁面作用时，在外海（G1）、礁前斜坡（G5）、礁缘（G7）、礁坪前部（G10）、礁坪中部（G14）和礁坪末端（G18）处自由液面高度（η）的时间序列。当波浪传播至G5 时，由于礁前斜坡的浅化作用波峰开始变陡，在礁缘G7 处已发生了破碎，表现为锯齿状；随后波浪以激波的形式在礁坪上传播。从G5 开始除了孤立波的首峰外，还出现了一个反向传播的次峰，这是由波浪在礁后岸滩处爬坡后的回落造成。粗糙礁面的影响从礁坪前部G10 开始向海岸方向逐渐变得显著，到岸滩坡脚G18 处入射波首波在粗糙礁面时显著降低，同时粗糙礁面的存在也相应地削弱了各位置的次峰值。最后还可以发现礁面糙率降低了波浪的传播速度，因此从G14 位置开始波浪在两种礁面下呈现出相位差。

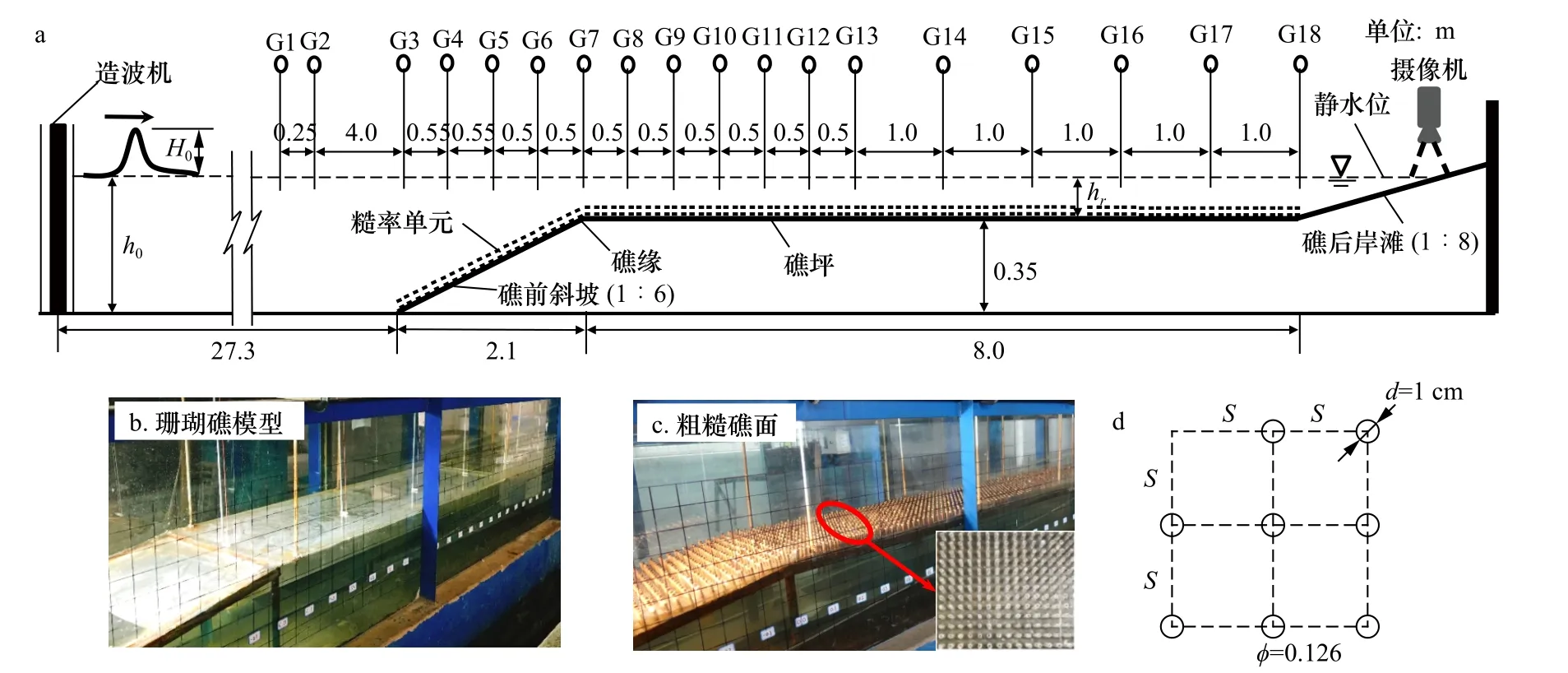
图1 物理实验设置Fig.1 Experimental setup

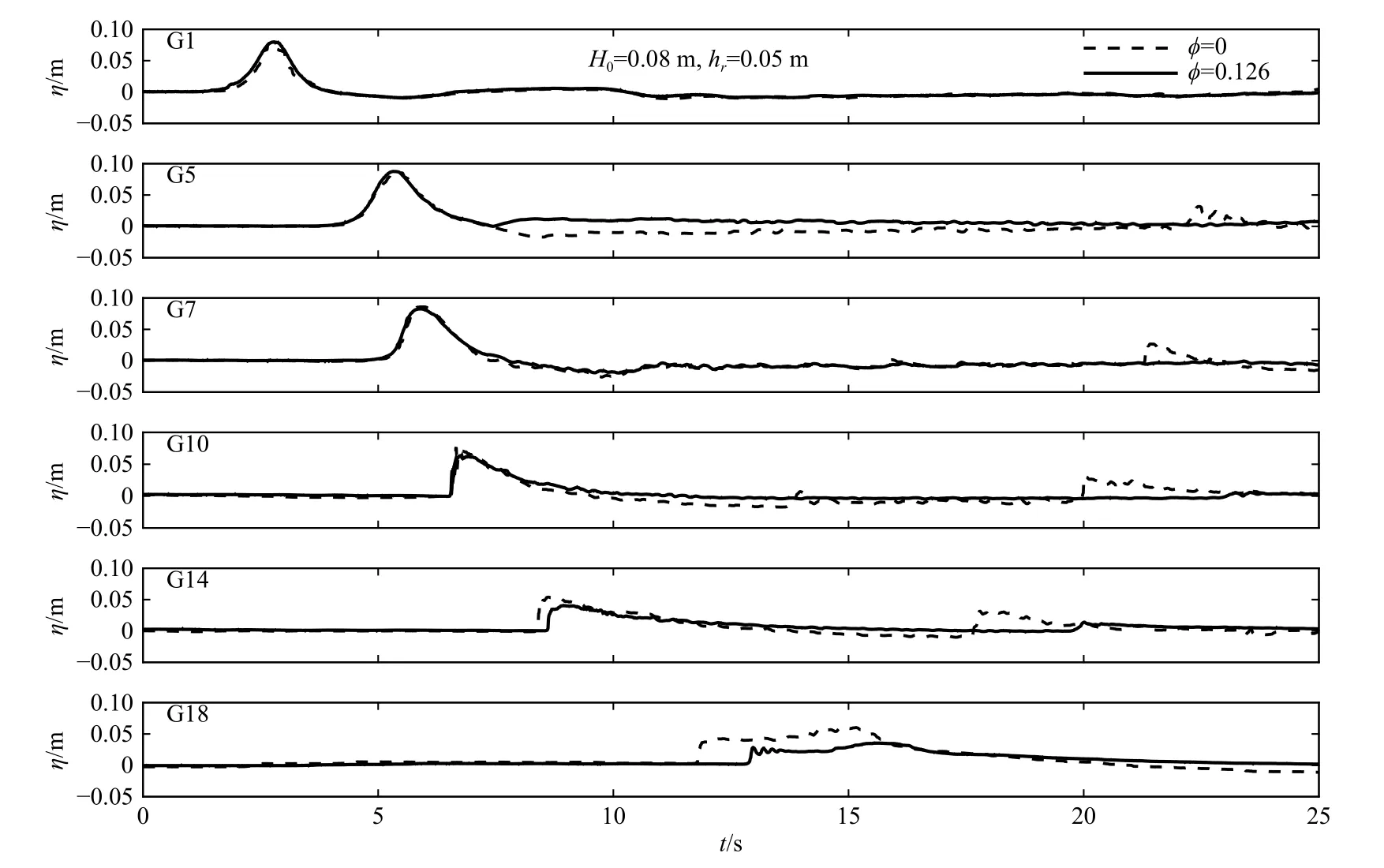
图2 垂直于岸线方向沿礁不同位置（G1、G5、G7、G10、G14、G18）自由液面高度(η)的时间序列Fig.2 Time series of free surface elevation (η) at different cross-shore locations (G1,G5,G7,G10,G14,G18) along the reef

3.2 波高垂直于岸线方向的沿礁变化

为了研究粗糙礁面（φ=0.126）上波高的衰减过程，图3a 和图3b 分别展示了礁坪水深hr=0.05 m 时不同入射波高影响下和入射波高H0=0.08 m 时不同礁坪水深影响下无量纲波高Hi/H0垂直于岸线方向的沿礁变化规律：当孤立波从深海传播到礁前斜坡时，由于浅化作用，波浪高度增加，并在礁前斜坡上开始发生破碎（最大的Hi/H0处），图3b 中hr=0.10 m 这一工况例外，此时由于水深较大波浪破碎发生在礁坪上。波浪破碎后在礁坪上传播，由于表面激波产生的湍流耗散和底部糙率造成的摩阻耗散共同作用，Hi/H0沿礁逐渐衰减。同时，从图3a 和图3b 中可以分别观察到：随着H0的增加，礁坪上Hi/H0减小，说明当入射波高较大时，在礁坪上的能量透射率更低；随着hr增加礁坪上Hi/H0增加，这是因为礁坪水深变大减弱了波浪破碎和底部摩擦引起的波能耗散。图3c 对光滑礁面（φ=0）和粗糙礁面（φ=0.126）进行了对比，从礁缘附近开始，由于摩阻耗散的增加，粗糙礁面上Hi/H0沿礁的衰减更为显著。

3.3 礁前斜坡的波浪反射

图4a 以入射波高H0=0.08 m 和礁坪水深hr=0.05 m的工况为例，展示了外海（G1）处自由液面的时间序列：自由液面的过程线存在两个明显的峰值，首先出现的为入射波，随后出现的为礁前斜坡反射造成的反射波。与入射波的定义类似，我们将反射波波峰与初始静水位之间的垂直距离作为反射波高HR，值得注意的是HR的值可能一定程度上会受到入射波尾波振荡影响。

图4b 展示了G1 处无量纲反射波高HR/H0即反射系数随着无量纲入射波高H0/h0的变化规律。H0/h0一定时，波浪在礁坪水深hr较小时的HR/H0要大于hr较大时，这是因为礁前斜坡在低潮位时对入射波的影响更加显著。同时在hr较小时，HR/H0随着H0/h0的增加而迅速减小，而在hr较大时，HR/H0随着H0/h0的增加缓慢增大，不同hr下的HR/H0最终趋向于一个常值约为0.08，这是由于大波高或高潮位时处于淹没状态的礁前斜坡反射影响有所减弱造成。对比光滑和粗糙礁面的情况可以发现：对于大多数测试工况，礁面糙率的存在略微增大了礁前斜坡的反射，这可能是由于糙率单元的存在增大了整个礁体的高度造成。

3.4 礁坪透射波高和礁后岸滩爬高

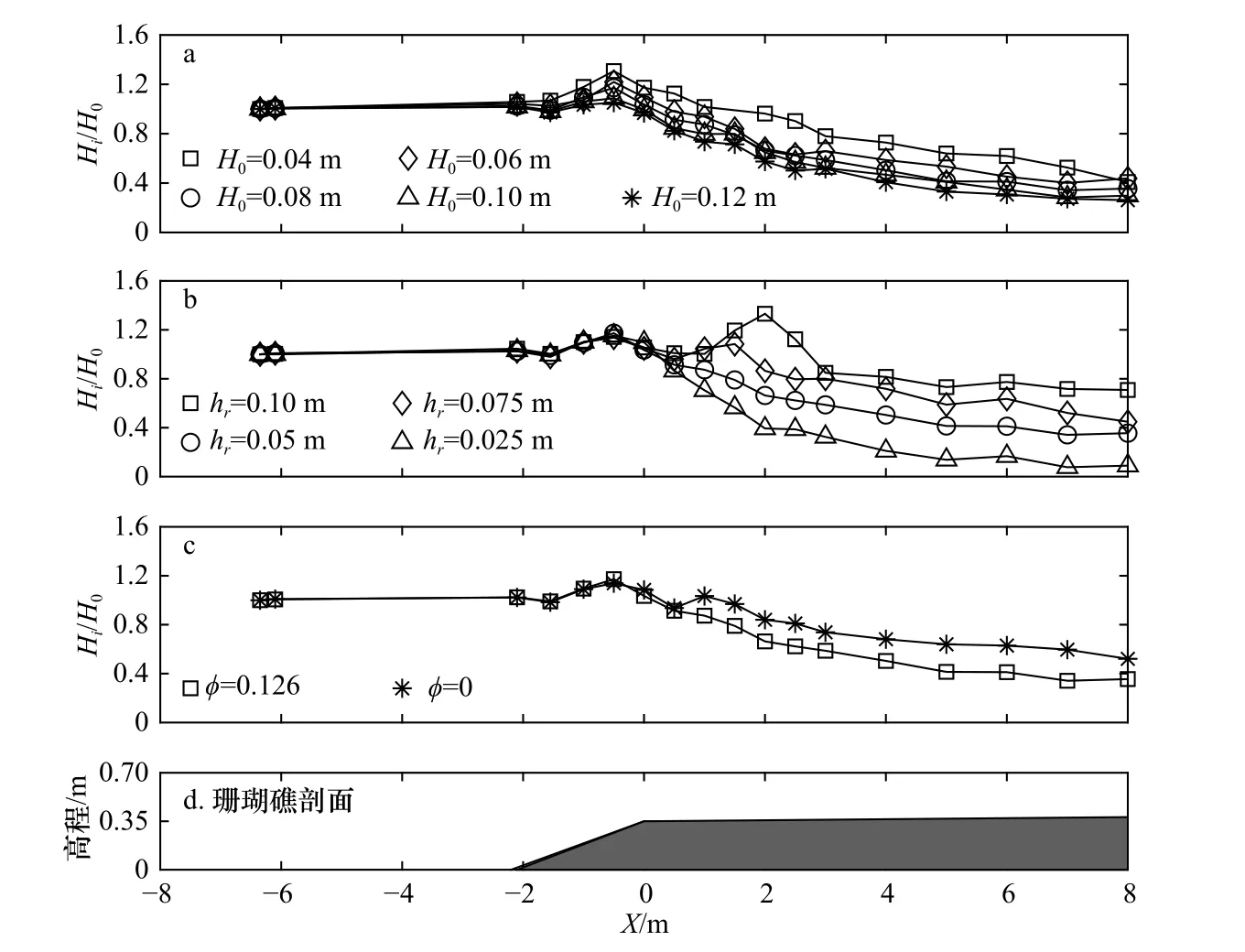
图3 无量纲波高Hi/H0垂直于岸线方向的沿礁（G1−G18）变化规律Fig.3 The cross-shore variation of normalized wave heights (Hi/H0) along the reef (G1−G18)

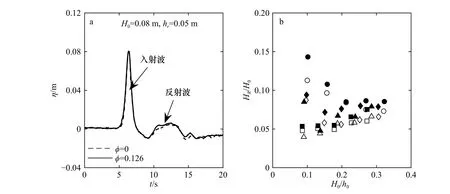
图4 外海G1 处自由液面（η）的时间序列（a）和无量纲反射波高HR/H0随无量纲入射波高H0/h0的变化（b）Fig.4 Time-series of the free surface elevation at offshore G1 (a),and variation of the normalized reflected wave height at G1 (HR/H0)with the normalized incident wave height (H0/h0)（b）

图5a 展示了粗糙和光滑礁面情况下礁后岸滩坡脚（G18）处，无量纲透射波高（H18/H0）即透射系数随无量纲入射波高（H0/h0）的变化规律。结果表明，H18/H0值的范围为0～1.67，说明入射波高在珊瑚礁上不一定表现为衰减，也可能会增长。H18/H0＞1通常发生在礁坪水深hr较大，H0/h0较小的工况，这主要是由于在大潮位情况下，入射波高较小的波浪在礁坪上发生传播变形时，由于波浪破碎和底床摩擦引起的波高衰减不足以抵消由于波浪在礁前斜坡上浅水变形引起的波高增大；当hr较大时，随着H0/h0值的增加，H18/H0下降迅速，当hr减小时，H18/H0下降趋势有所减缓；同时通过对比发现粗糙礁面时的H18/H0要显著低于相同情况光滑礁面时的H18/H0。

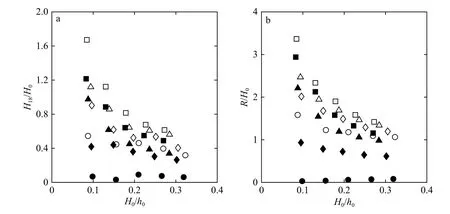
图5 礁后岸滩坡脚（G18）处无量纲透射波高（H18/H0）随无量纲入射波高（H0/h0）的变化（a），岸滩爬高（R/H0）随无量纲入射波高（H0/h0）的变化（b）Fig.5 Variation of the normalized transmitted wave height at the toe of back-reef beach (G18) (H18/H0) with the normalized incident wave height (H0/h0) (a),and variation of the wave run-up on the back-reef beach (R/H0) with the normalized incident wave height (H0/h0) (b)

图5b 中展示了无量纲岸滩爬高（R/H0）随无量纲入射波高（H0/h0）的变化规律。正如预期的那样，R/H0的变化趋势与图5a 中的无量纲透射波高一致；R/H0的值最高达到3.4，说明礁后岸滩孤立波的爬高可能是入射波高的几倍，且发生在hr最大时，因此在评估海啸减灾时，应特别关注大波高与高潮位同时发生的情况。图5b 也表明粗糙礁面上R/H0的值均小于相同情况下光滑礁面的值，对于本文测试的粗糙礁面上波浪爬高值的平均减小幅度达到46%，这意味着实际珊瑚礁上产生大糙率的珊瑚群落的存在对防治海啸灾害起着积极的作用。

4 有关孤立波爬高的进一步讨论

对于平直海岸，Synolakis[11]提出下列经验公式来预测孤立波爬高

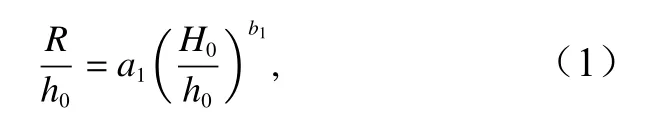
式中，系数a1和b1为经验参数。基于本文实验数据根据公式（1）描述的R/h0与H0/h0的关系如图6a 所示。可以观察到图中的数据离散度比较大，因此公式（1）不适用于珊瑚礁地形。以往的研究表明礁坪相对水深hr/H0是描述波浪在珊瑚礁上水动力特性的一个重要参数[12-13]。Yao 等[9]基于此参数，提出了适用于孤立波与光滑珊瑚礁面相互作用时预测波浪爬高的经验关系式

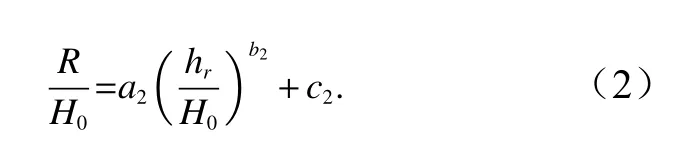
对于本文研究的粗糙礁面，hr实际的礁坪水深应为糙率单元淹没深度，即原始光滑礁坪淹没度减去粗糙单元高度（本文为2.5 cm）。公式（2）表示的无量纲爬高与礁坪相对水深的关系如图6b 所示。可以发现公式（2）可以分别较好地描述本文光滑和粗糙礁面的实验数据，但两组数据不能聚合在同一条线上。因此对公式（2）通过进一步加入糙率密度参数 φ来描述礁面粗糙度的影响，经回归分析得到预测无量纲爬高的幂函数型经验公式关系为

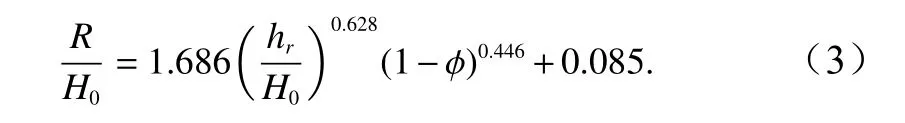
拟合精度为R2=0.96。图6c 展示了根据公式（3）计算的无量纲爬高预测值与实验测量值的比较，两者符合较好，表明公式（3）可以较好地预测不同礁面粗糙度时孤立波在礁后岸滩上的爬高，值得说明的是公式（3）根据本试验的测试仅考虑了入射波特征参数和礁面糙率的影响，进一步对其的改进可以加入其他的礁形参数（礁坪宽度、礁前斜坡坡度）的影响以及考虑潟湖和/或防浪建筑物的存在。

5 结论

本文通过波浪水槽物理模型实验对礁面大糙率影响下孤立波在珊瑚礁地形上传播变形及岸滩爬高的变化规律进行了研究，并与光滑礁面进行了对比，结果分析表明：

（1）孤立波破碎后以激波的形式在礁坪上传播，粗糙礁面的存在显著削弱了礁坪上孤立波的首峰和礁后岸滩反射造成的次峰，同时降低了波浪在珊瑚礁面的传播速度；

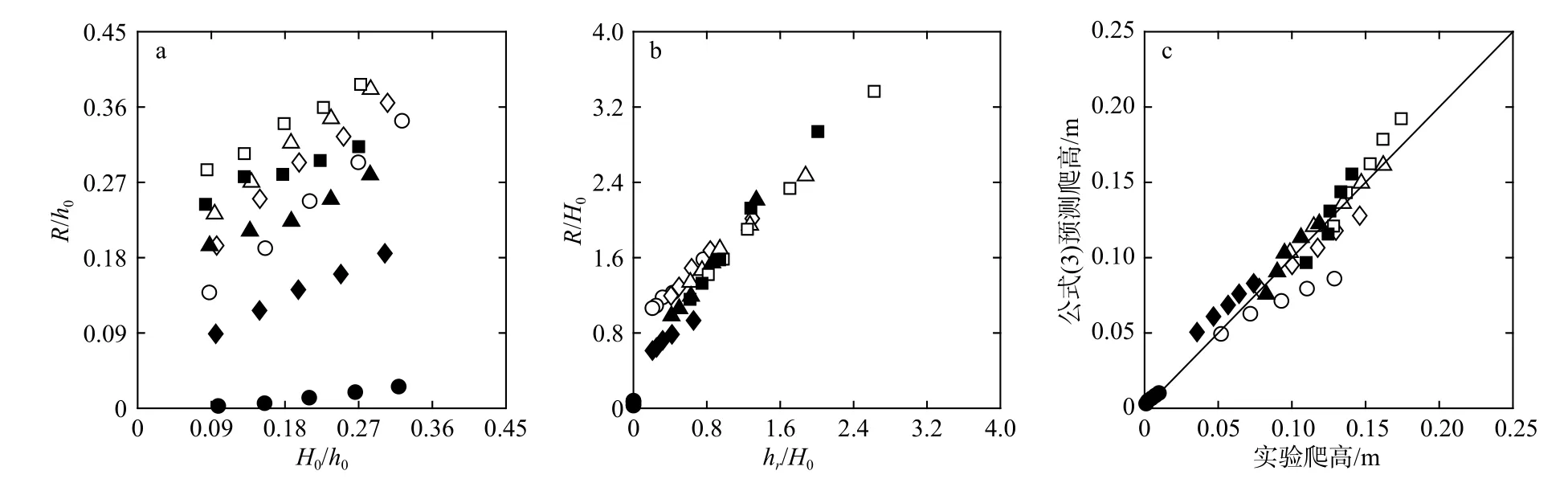
图6 无量纲礁后岸滩爬高（R/h0）随无量纲入射波高（H0/h0）的变化（a）；无量纲礁后岸滩爬高（R/H0）随相对礁坪水深（hr/H0）的变化（b）；基于公式（3）的预测值与实验测量爬高对比（c）Fig.6 Variation of the normalized wave run-up on the back-reef beach (R/h0) with the normalized incident wave height (H0/h0) (a);variation of the normalized wave run-up on the back-reef beach (R/h0) with the relative reef-flat water level (hr/H0) (b);comparison between the predicted wave run-ups based on Eq.(3) and the measured wave run-ups (c)

（2）垂直于岸线方向沿礁相对波高随着入射波增大而减小，随着礁坪水深的增大而增大，粗糙礁面上波高沿礁的衰减更为显著；

（3）礁前斜坡的无量纲反射波高随无量纲入射波高的变化与礁坪水深有关，当入射波高足够大时其趋向于一个常值，粗糙礁面略微增大了礁前斜坡的反射；

（4）无量纲透射波高和无量纲岸滩爬高随着无量纲入射波高的增大而减小，特别是礁坪水深较大时更为显著，无量纲岸滩爬高在粗糙礁面相对于光滑礁面平均减小幅度达到46%；

（5）通过回归分析得出了同时适合于光滑和粗糙礁面的预测孤立波岸滩爬高的幂函数型经验关系式。