考虑黏弹性边界及缝面水压的重力坝地震开裂模拟

徐 浩 江守燕 杜成斌

(河海大学 工程力学系,南京 210098)

大坝作为挡水建筑物,在调节水资源、航运、发电等领域都发挥着举足轻重的作用,因此如何准确评估大坝抵御地震荷载的能力是水利水电工程抗震问题的研究重点[1].传统有限元法模拟裂缝扩展等不连续问题时需不停地进行网格重划分,Belytschko等[2]提出的扩展有限元法(extended finite element methods,XFEM)可以使裂纹扩展的几何路径独立于网格,避免了网格重划分,极大地提高了运算效率.杜效鹄等[3]结合扩展有限元法对重力坝动态响应进行了数值模拟;董玉文等[4]推导建立了满足大坝水力压裂问题的扩展有限元法;高景泉等[5]研究了静力作用下重力坝踵预设裂缝的水力压裂问题;庞林等[6]基于比例边界有限元法研究了缝水压力和裂缝面接触条件对重力坝裂缝扩展的影响;李宗利等[7]研究了混凝土重力坝裂缝面上施加不同水压分布形式的稳定性情况,这些研究均为地震作用下坝体水力劈裂研究奠定了重要基础.

重力坝地基边界模拟和地震荷载输入方式是大坝地震响应分析的关键,对数值模拟结果的准确性有着直接的影响.目前,动力人工边界主要有透射边界[8]、无限元边界[9]、黏性边界[10]、黏弹性边界[11]等.透射边界应用较复杂,且通常只限于二阶精度以内,可能存在高频失稳的问题;黏性人工边界忽略了弹性恢复力,只考虑阻尼吸收作用,容易出现结构整体漂移,不宜应用在较复杂的大型结构中.黏弹性人工边界较于黏性边界避免了低频失稳问题,同时可以模拟截断边界上弹性恢复力和无限远场散射辐射,具备了较高的精度和稳定性,黏弹性边界最早由Deek和Randolph提出,随后刘晶波和吕彦东[12]在此基础上研究并提出了三维时域黏弹性边界[13].地震荷载输入方法在ABAQUS中有两种不同的实现思路,苑举卫等[14]通过ABAQUS中的DLOAD和UTRACLOAD两个子程序实现,而何建涛等[15]是计算每个节点在每一时刻对边界的作用力,并将其作为振幅数据导入ABAQUS中,应用到每个相应的结点上.

本文采用扩展有限元法仿真模拟混凝土重力坝的地震开裂过程,根据波场分离理论和与黏弹性人工边界相适应的地震动输入公式,结合ABAQUS二次开发功能,利用Matlab编写相应的边界条件自动施加和地震动输入程序,分析探讨不同的抗震分析模型对大坝地震开裂过程的影响.

1 动力扩展有限元法

1.1 位移模式

对于裂纹问题,XFEM位移模式可以表示为:

式中:Ni(x)为常规有限元插值形函数;ui为常规结点自由度;ai为与跳跃函数有关的附加自由度;bli为裂尖附加自由度;Ω为所有离散节点的集合;ΩΓ为裂纹贯穿单元的结点集;ΩΛ为裂尖单元的结点集.H(x)为Heaviside函数,是反映裂纹面位移不连续的一个附加函数,分别取裂纹面上、下侧的+1和-1来反映位移不连续性,定义为

式中:r、θ分别为裂尖局部极坐标半径、夹角.

1.2 控制方程

因缝水压力为结构所受外荷载,故作为面力施加到裂缝面,且作用于增强自由度上.因此参照文献[16],可以假定缝面水压力P的分布形式为:

式中:r为开裂缝面上节点到裂纹尖端的距离;a为裂缝长度;P0为裂纹开口处的静水压力;论文采用均匀分布水压,故n取0.

考虑阻尼的影响,由弹性动力学的基本方程[17]及XFEM位移模式,运用虚功原理[18],可得动力XFEM的控制方程为:

采用Newmark隐式时间积分算法进行时间离散[19],假设

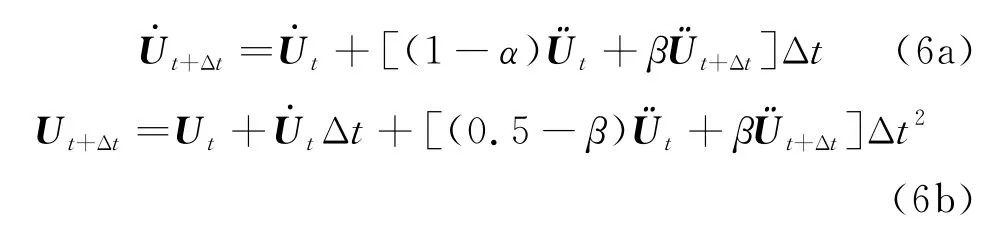
式中:α和β为积分常数,与积分精度和数值稳定性有关,α=0.25(1-δ)2,β=0.5-δ,且δ∈[-1/3,0].

Newmark隐式时间积分算法是无条件稳定的,

式中:x为观测点;x*为观测点在裂纹面上的投影点;n为x*处裂纹面的单位外法向.

建立以裂尖为坐标原点的(r,θ)极坐标系,则裂纹尖端附加函数Fl(x)由下列4个基函数组成:结果的稳定性与时间步长无关,时步长的选取依赖于求解精度,文中取δ=-0.05.

1.3 裂纹开裂准则

ABAQUS中基于拉伸分离损伤法的初始损伤准则有6种,但只有最大主应力准则和最大主应变准则可用于模拟裂纹扩展等不连续问题.选择最大主应力准则[20]作为裂纹开裂的判据,可表示为

2 黏弹性人工边界及地震动输入模型

2.1 黏弹性人工边界模型及实现

通过在边界上设置连续分布的并联弹簧阻尼单元来实现黏弹性人工边界(如图1所示).

图1 黏弹性边界弹簧-阻尼器单元

其中弹簧和阻尼器的力学参数由围岩材料参数所决定,可通过下式计算[21]

式中:KBT、KBN分别为弹簧在切向和法向的刚度系数;CBT、CBN分别为阻尼器在切向和法向的阻尼系数;αT、αN为修正系数,一般情况下,αT、αN的取值参考刘晶波等[22]的研究,取αT=0.5,αN=1.0;R为边界点与波源的距离;ρ、G分别为材料的密度和剪切模量;Cs和Cp分别为材料的剪切波速和纵波波速,可表示为

式中:E、λ、μ分别为介质的弹性模量、Lame常数和泊松比.

利用有限元软件ABAQUS中提供的弹簧单元和阻尼器单元,可以实现截断边界上各结点弹簧单元和阻尼单元的施加.文中基于MATLAB语言编写了批量自动施加黏弹性边界的程序,首先读取边界结点坐标,然后根据式(8)计算出弹簧刚度系数和阻尼系数,最后通过修改ABAQUS中的输入数据文件完成所有边界结点处弹簧和阻尼单元的施加.

2.2 地震动输入模型及实现

根据波场分离,截断边界上的波可分解为散射场与自由场,在黏弹性边界上设置自由场时自动满足散射场,将外源地震波输入到了有限域地基内.人工边界上的等效结点荷载通过下式计算得到[23]

式中:KB为刚度系数;CB为阻尼系数为该人工边界点的自由场位移为该点的自由场速度为该点应力;n为该点外法线方向余弦.

根据弹性力学理论,结合底边位移边界条件和波动理论,首先计算应变,然后由应力-应变关系求出应力,再由边界结点平衡关系得到边界结点上的等效结点力,具体边界结点力计算公式可参见文献[24].

文中采用的方法是提前计算人工边界上各点随时间变化的切向与法向荷载数值,利用ABAQUS软件中的指令在边界点上输入随时间变化的等效荷载.具体做法是:首先提取坝体模型的尺寸大小、材料参数值、单元结点坐标和编号、结点控制面积大小、地震波的位移和速度时程曲线;然后利用式(8)中的弹簧刚度系数和阻尼系数计算值,结合地震波处理软件SeismoSignal分时段积分得到的速度与位移时程,推导出地震在自由场产生的应力以及弹簧和阻尼单元产生的附加应力;最后与提取得到的结点控制面积相乘,得到边界上各结点的等效荷载时程情况,通过在原有模型文件中插入新的inp计算文件,在ABAQUS求解器提交运算即可.

2.3 程序验证

假设一个二维弹性矩形体,从底部边界垂直入射地震波,则该入射波位移函数为:

弹性体长为762 m,宽为381 m,质量密度ρ=2.7 kg/m3,弹性模量E=13.23 MPa,泊松比ν=0.25,P波波速cP=2 425 m/s,SV波波速csv=1 400 m/s.假定为平面应变问题,弹性体被离散成76×38个四边形等参元,底边分布76个黏弹性单元,左、右侧边各分布38个黏弹性单元.二维弹性体网格图及计算波形分别如图2、3所示,计算时间增量Δt为0.005 s,模拟过程总时长t为2 s.

图2 二维弹性体网格图

图3 入射波位移时程曲线

数值计算结果如图4所示,上边界A、B、C3个观测点位移幅值接近于入射波位移幅值的两倍,这一现象证实了入射波传播至上边界后形成反射波,波形叠加形成了上边界各点的位移时程曲线,0.75 s后3个观测点都不再有位移变化,这表明反射波抵达底部边界后可以被黏弹性边界充分吸收,之后不再反射.

图4 理论解与数值解的比较

相比于上边界各点波形叠加只形成了单个波峰,底部边界上D、E两点均有一前一后两个波峰,可以看出入射波在形成第一个波峰之后,经上边界反射之后在下边界又形成了一个波峰.另外,同一水平位置观测点的位移曲线规律基本相同,说明波的传播是均匀的.该数值结果与波传播规律的理论解基本一致,说明文中所应用的程序与模拟方法是正确可行的.

3 重力坝地震开裂模拟

以Koyna重力坝为研究对象,图5(a)为该重力坝的几何模型及尺寸,大坝坝高103 m,坝顶宽度14.8 m,坝底宽70 m,地震时库水位为91.75 m,上游面垂直,下游面折坡点以上部分坡比为1∶0.12,以下部分坡比为1∶0.76.坝体混凝土材料弹性模量为31.027 GPa,泊松比为0.15,质量密度为2 463 kg/m3,抗拉强度为2.9 MPa,抗压强度为24.1 MPa,断裂能为250 N/m.坝基岩体的弹性模量为24 GPa,泊松比0.25,质量密度为2 500 kg/m3.参照文献[17],为便于研究和对比,假定坝体上游面距离坝踵20 m处有一水平预设裂纹,长度设为8 m.图5(b)为坝体-地基系统网格,坝基系统离散成四结点平面等参元,共3 794个单元,3 986个结点,地基范围向上游面、下游面以及深度方向延伸3倍坝高.

图5 重力坝坝体几何模型及坝基系统网格

在进行数值计算时,施加的荷载包括坝体自重、上游面静水压力、地震荷载以及动水压力.地震波采用Koyna地震实测地震波,水平向峰值加速度为0.49g,竖向峰值加速度为0.34g,如图6所示.动水压力采用附加质量法近似模拟.计算总时间为10 s,计算时间增量为0.01 s.根据加速度时程曲线分时段积分得到速度与位移时程,再根据底边与侧边各点速度和位移计算出等效荷载实现地震波输入.

图6 输入的Koyna地震波

文中分析探讨了3种模型对大坝地震开裂的影响,模型1为无质量地基模型且缝面无水压;模型2为无质量地基模型缝面有水压;模型3考虑缝面有水压的同时,地基采用有质量弹性地基并设置黏弹性人工边界,地震波输入采用等效荷载形式.采用黏弹性人工边界时,底边与侧边共有黏弹性单元83个.

图7给出了坝顶观测点A在3种模型下的水平位移时程曲线,可以看出缝面有无水压两种情况的位移变化规律大致一样,有水压的位移幅值比无水压的位移幅值高出26.1%,且二者出现位移幅值的时间与预设裂纹长度骤然增加的时间相吻合,这表明无质量地基模型在8～9 s之间地震响应最明显.考虑了黏弹性边界的位移幅值较不考虑黏弹性的位移幅值显著降低,说明采用无质量刚性地基重力坝抗震模型相较于黏弹性地基模型,放大了地震动响应.

图7 观测点A的水平位移时程曲线

图8给出了3种模型下的裂纹扩展路径,图9对比了3种模型下的裂纹开裂扩展路径.

图8 地震开裂扩展路径

图9 3种模型下裂纹开裂扩展路径对比

从图中不难看出裂纹面上有水压时的偏转角要小于无水压时的结果,这个结果与文献[24]中得到的结果相一致,而考虑黏弹性边界且采用有质量弹性地基时的裂纹扩展路径则比较平缓,偏转角也要小于不考虑黏弹性边界时的结果.分析裂纹路径成因,可能由于惯性力周期性变化,因此在开裂初期不断由上游面向下游面扩展,在裂纹扩展前期,自重引起的压力作用导致裂纹闭合,故裂纹沿水平方向延伸,保持了坝体的基本稳定.而在后期裂纹在扩展中开裂路径并非水平延伸,而是斜向下延伸,推测原因是裂纹尖端区应力需受惯性力和坝体自重叠加影响,而在裂纹扩展后期裂纹尖端区应力受惯性力影响减弱,坝体自重影响增大,故裂纹向右下方延伸.

图10对比了3种模型下的裂纹开裂扩展路径,给出了裂纹长度随时间的变化曲线,容易看出缝面有水压时裂纹的开裂距离大于无水压的开裂距离,分析其原因,是由于外法向水压作用于裂纹表面,相当于增加了Ⅰ型裂纹开裂的驱动力.此外考虑黏弹性边界时的裂纹开裂长度小于无质量地基模型的结果.

图10 裂纹长度随时间变化曲线

图11是3种情况的裂缝宽度变化情况,不难发现三者的扩展规律相一致,都是裂纹宽度越接近裂尖位置越小,缝面有水压时裂纹扩展宽度明显大于无水压情况,这是因为裂纹面上施加了外法线方向的水压力,水压的驱动力必然引起法线方向的扩展宽度变大.考虑黏弹性边界时的最大裂纹宽度小于无质量地基模型的结果,减小了约19%.

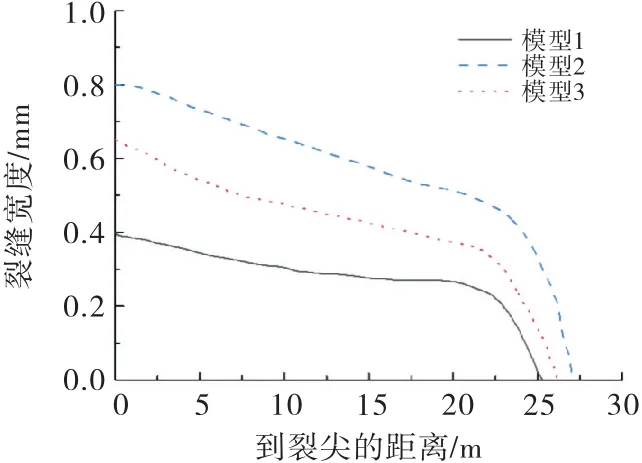
图11 3种模型下裂缝宽度变化对比

4 结 论

采用扩展有限元法仿真模拟了混凝土重力坝的地震开裂过程.分析探讨了3种模型对大坝地震开裂过程的影响:1)无质量地基模型且缝面无水压;2)无质量地基模型且缝面有水压;3)缝面有水压且考虑黏弹性人工边界有质量地基及地震动等效荷载输入的抗震计算模型.

仿真模拟结果表明:1)黏弹性人工边界模型计算得到的位移幅值较无质量地基模型的结果小,即无质量刚性地基抗震分析模型放大了大坝的地震动响应;2)缝面有水压时的裂纹偏转角小于无水压时的结果,而考虑黏弹性边界且采用有质量弹性地基时的裂纹扩展路径则更平缓;3)缝面有水压时裂纹的开裂距离大于无水压时的开裂距离,考虑黏弹性人工边界时的裂纹扩展长度小于无质量地基模型的结果;4)缝面有水压时裂纹扩展宽度明显大于无水压情况,考虑黏弹性边界时的最大裂纹宽度小于无质量地基模型的结果,减小了约19%.

此外,库水的可压缩性对重力坝地震开裂也有一定影响,在今后的研究中将进一步考虑大坝-地基的流固耦合效应,探讨无限库水的影响.