某型电动飞机起飞加速特性分析与仿真模型修正
张钧尧,佟刚,李亚东,2,王锋,周国庆
(1.沈阳航空航天大学辽宁通用航空重点实验室,沈阳110136)
(2.沈阳飞机设计研究所 飞行控制部,沈阳110035)
0 引言
飞机对改善人类生活和促进经济发展起到了至关重要的作用,但也对生态环境造成了许多负面影响[1-3]。电动飞机零排放、低噪声,对环境几乎没有负面影响。因此国内外相关机构投入大量资源对电动飞机进行技术攻关[4]。
起飞是飞机飞行中至关重要的阶段,也是最容易发生事故的阶段之一。起飞场长和地面滑跑距离是机场和飞机设计公司仿真模型中常见的参数。完全通过飞行试验来收集这些数据是非常耗时且昂贵的,因此许多国内外学者对起飞性能仿真模型展开了一系列研究。国外,D.Zammit-Mangion等[5-6]评估了克兰菲尔德大学开发的大型运输机起飞性能计算程序,并与早期双涡轮螺旋桨飞机起飞性能计算程序进行了对比,为了对飞机性能进行实时监视,提出了一种使用速度分布二阶近似值计算飞机起飞性能的简化算法,并检验了该简化算法的准确性;K.Orleans等[7]介绍了一种替代标准化起飞性能计算的方法,该方法使用建模仿真来校正非标准环境因素,例如风速、跑道坡度和飞机起飞总重等因素对起飞性能的影响,并使用涡轮螺旋桨战术运输机来验证此方法;N.F.A.B.Elmajdub等[8]基 于MATLAB软 件 的SIMULINK模块,搭建了飞机起飞降落阶段的可视化自动控制模型。
国内对于起飞性能仿真和优化也开展了一系列的研究工作,林可心等[9]建立了飞机起飞着陆过程的微分方程,使用SIMULINK对起降性能进行建模仿真,通过对比飞行过程中记录的数据和仿真结果验证了模型的准确性;吴大卫等[10]针对小型无人倾转旋翼机建立了短距起飞仿真模型,为了得到最短的起飞距离,使用遗传算法对操纵变量进行优化;郑峰敏[11]根据两点式起飞和三点式起飞的运动特点,在MATLAB中建立了两种起飞方式的动力学模型,分析了两种起飞方式对飞机起飞性能的影响;李亚东等[12]基于电动飞机输出功率、总体参数、气动参数、螺旋桨的效率以及锂电池能量密度等特点,采用Simpson积分法和Run⁃ge-Kutta法计算了电动飞机起飞爬升性能,并通过对比飞行试验数据验证了模型的准确性。上述研究都是将飞机起飞滑跑过程简化成匀加速直线运动,这与飞机真实起飞情况存在一定差异,将这类仿真模型简称为近似匀加速仿真模型。魏志强等[13]针对大型民用客机建立了一种加速度估算模型,该估算模型的准确性优于近似匀加速仿真模型,但也存在一定的不足,例如需要以大量的起飞数据为基础,并且难以量化风速、飞机质量改变等因素对飞机起飞性能的影响。
虽然国内外在电动飞机研制方面取得了一定成果,但偏向于工程应用。上述研究对象绝大多数都是油动飞机,国内鲜见纯电动飞机起飞性能仿真方面的研究文献。
本文针对电动飞机在MATLAB中建立完整起飞过程的仿真模型,根据电动飞机飞行试验采集的加速度与速度数据使用数值拟合的方式对仿真模型中速度进行修正;分别使用修正前后的模型对某型电动飞机起飞性能进行仿真计算,并与飞行试验数据进行对比;使用修正后的模型分析风速、电动机功率以及飞机质量对该型飞机起飞性能的影响。
1 电动飞机起飞模型建立
1.1 飞机起飞过程分析
电动飞机与传统油动飞机在计算起飞性能时主要有两点不同:①电动飞机中电动机替代了燃油发动机,燃油发动机最大功率会随着飞行速度的变化而变化,而电动机的最大功率在计算起飞性能时可以认为是一个常量;②传统油动飞机重量和重心会随着燃油的消耗而改变,而电动飞机的重量和重心在飞行过程中并不会随着电量消耗而改变。
根据起飞过程的运动特点,可以将起飞分为两点式起飞和三点式起飞[14]。本文探讨三点式起飞,起飞过程如图1所示。三点式起飞可以分为三个阶段:三轮滑跑阶段、两轮滑跑阶段以及起飞空中阶段。

图1 三点式起飞过程Fig.1 Three-point takeoff process
(1)三轮滑跑阶段
飞机从静止开始起跑,速度逐渐增大。当飞机速度增至抬前轮速度(VR)时,驾驶员操纵飞机抬起前轮,该阶段结束[15]。在飞机飞行性能计算手册及美国联邦航空条例(FAR)第25部中明确规定,民用飞机抬前轮速度为

式中:VR为飞机抬前轮速度;VS为失速速度,工程初算时抬前轮速度在初算可取平均值1.15VS。

式中:G为飞机质量;CLmax为配平后的最大升力系数;ρ为机场当地空气密度;S为机翼面积。
可用拉力计算公式为

式中:Tky为可用推力;P为电机功率;η为螺旋桨效率;V为飞机速度。
使用Runge-Kutta法求解微分方程组:

式中:L1为三轮滑跑阶段的地面滑跑距离;VW为风速,规定逆风为正;g为重力加速度;α为飞机迎角;φP为推力作用线与飞机迎角基准之间的夹角;φ为跑道坡度,规定向上为正;f为滑跑时的地面摩擦系数;CD、CL分别为阻力系数和升力系数。
给定初始条件t=0,V=0,L1=0,终止条件V=VR,可以得到V(t)和L1(t),进而得到地面滑跑距离和时间。
(2)两轮滑跑阶段
飞机抬起前轮后,保持两主轮接地继续加速滑跑,随着速度的增加,飞机升力也逐渐增加[16-17]。当速度达到离地速度以后,飞机的升力等于重力,主轮离开地面,地面滑跑结束。飞机飞行性能计算手册中明确规定,民用飞机离地速度:
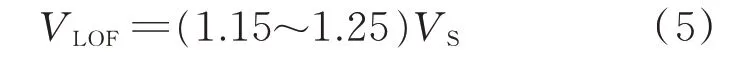
式中:VLOF为飞机主轮开始离地时的速度,也称为飞机离地速度,在工程初算时可取平均值1.2VS。
初 值 条 件t=0,V=VR,L2=0,终 止 条 件V=VLOF时,使用Runge-Kutta法求解微分方程组:

式中:L2为两轮滑跑阶段的地面滑跑距离。
飞机在两轮滑跑过程中迎角逐渐增大,为了简化模型该过程迎角取平均值,CL、CD分别取平均仰角对应的升、阻力系数,进而得到滑跑距离和时间。
(3)起飞空中阶段
地面滑跑结束以后,飞机进入加速爬升阶段。当飞机高度达到安全高度15 m后,起飞过程结束[18]。这个过程是变加速爬升,为确定飞机的飞行轨迹建立质心的运动方程,初始条件t=0,V=VLOF,L3=0,终止条件H=15 m时,使用Runge-Kutta法求解微分方程组:
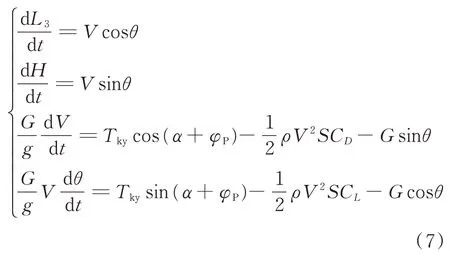
式中:L3为起飞空中阶段飞机在x方向的水平距离;H为飞机在y方向的飞行高度;θ为爬升角,为了简化模型,假设爬升角不发生改变,即
1.2 模型求解思路
模型求解思路为:确定可用推力、迎角以及升力系数阻力系数随速度的变化关系;地面滑跑阶段,通过速度是否达到离地速度来判断地面滑跑是否结束[19];起飞空中阶段,通过高度是否达到安全高度来判断起飞过程是否结束[20]。模型求解流程图如图2所示。
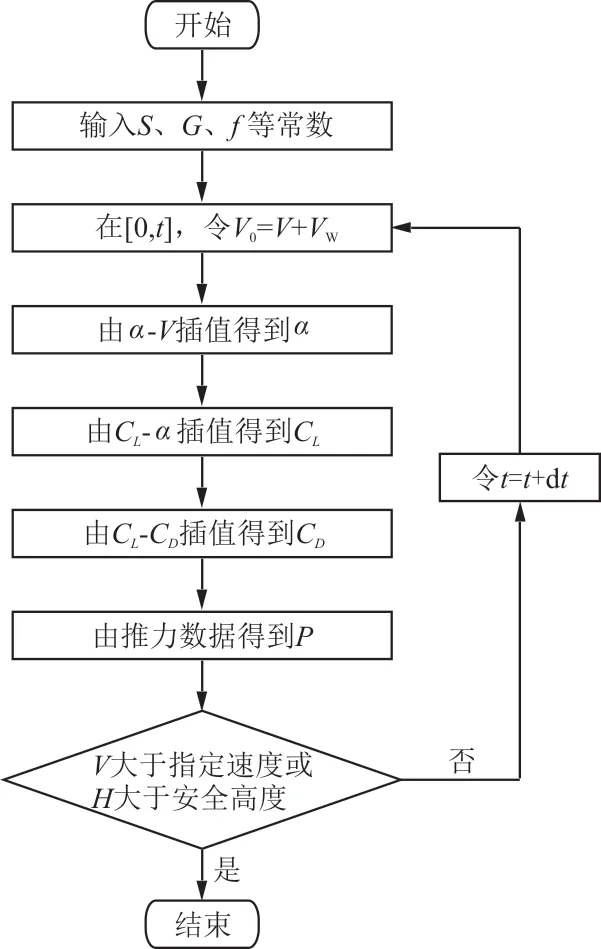
图2 模型求解流程图Fig.2 Flow chart of program calculation model
2 仿真模型误差分析
在第1节中介绍了一种工程中常用的起飞性能计算方法,适用于初算或者粗略计算。该方法只考虑主要影响因素,将飞机起飞过程简化为近似匀加速直线运动,但在实际起飞过程中由于发动机推力是油门和速度的函数,气动阻力和升力是速度的二次函数,而且由于飞机对于跑道的压力不断在变化,跑道对飞机的摩擦力也在不断变化,并且起飞空中阶段爬升角始终在变化。因此,实际起飞过程不可能是匀加速直线运动,将起飞模型简化为近似匀加速运动将带来一定误差。通过大量对比仿真结果与快速数据记录仪(QAR)记录的飞行数据,发现某客机计算结果中起飞场长与地面滑跑距离总是略小于实际的起飞场长和地面滑跑距离,误差约占实际距离的10%[13]。计算电动飞机起飞性能时也发现了类似的情况,即仿真结果中的起飞场长与地面滑跑距离总是小于试飞试验数据中的起飞场长和地面滑跑距离。
综上,近似匀加速仿真模型误差是对实际问题进行抽象、简化而导致的模型误差。
3 仿真模型修正
电动飞机的研制是一个反复迭代、逐渐逼近最优解、最终满足设计要求的过程。起飞性能仿真模型的建立也是一个逐步完善的过程。初算时模型中相关系数往往在飞行性能计算手册限定范围内取平均值或根据经验选取。试飞结束后,再根据试飞采集数据对仿真模型中相关系数进行一定的修正。由于近似匀加速模型存在一定的模型误差,同时在工程计算时往往难以建立完全符合实际起飞运动变化规律的物理模型。因此为了得到更准确的仿真模型,采用试飞采集的相关数据对近似匀加速模型进行修正。
3.1 起飞加速特性分析
为了研究电动飞机起飞过程中的加速特性,将某电动飞机试飞时采集的加速度数据进行整理,在MATLAB中使用Smooth函数以及Filter Design&Analysis Tool工具对采集的数据进行平滑、滤波处理,得到试飞采集的加速度和滤波处理后的加随时间变化的结果,如图3所示。

图3 真实加速度变化Fig.3 True acceleration variation
从图3可以看出:在0~10 s,加速度保持相对平稳;在10~18 s加速度随时间上下波动但总体呈现增长趋势;在剩余时间内,加速度呈现递减趋势且存在一定的波动。
仿真速度与试飞采集速度对比结果,如图4所示。将起飞过程中飞机的速度分为地面阶段和空中阶段来研究。地面阶段开始时真实速度与仿真模型速度都为0,此后真实速度大于仿真速度且速度差距逐渐增大;直到滑跑过程中间时刻,真实速度与模型仿真速度差距达到最大;此后真实速度与仿真速度差距越来越小,在结束时,真实速度与仿真速度十分接近,真实速度略大于仿真模型速度。起飞空中阶段开始真实速度与仿真速度十分接近,此后仿真模型速度大于真实速度,且差距越来越大,在起飞空中阶段结束时速度差距达到最大。

图4 速度对比Fig.4 Speed comparison
3.2 修正函数的构建
为了采用试飞数据对起飞性能仿真模型进行修正,引入修正函数的概念。修正函数反映近似匀加速仿真模型中速度与真实试飞速度的差异。修正后的速度为
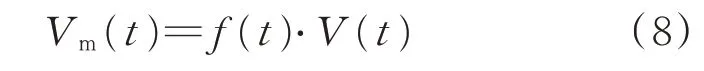
式中:Vm(t)为修正后的速度函数;f(t)为引入的修正函数。
理想的修正函数为真实速度与近似匀加速仿真模型速度的比值。使用多项式插值法拟合理想的修正函数,发现起飞地面阶段的修正函数近似于抛物线,起飞空中阶段的修正函数近似于直线。再结合加速度、速度的变化规律,可以将地面滑跑阶段的修正函数简化为满足如下条件的二次函数:起飞滑跑开始和滑跑结束时,即t=0和t=tLOF时,函数值为1;在地面滑跑的中间时刻,即t=时,真实速度与仿真速度误差达到最大,函数值为此时真实速度与仿真速度的比值。将起飞空中阶段的修正函数简化为满足如下条件的一次函数:从飞机离地这一瞬间开始,即t=tLOF时,函数值为1;在到达安全高度(15 m)时,函数值为此时真实速度与仿真速度的比值。修正函数如图5~图6所示。

图5 地面段修正函数Fig.5 Modified function in the ground segment during takeoff
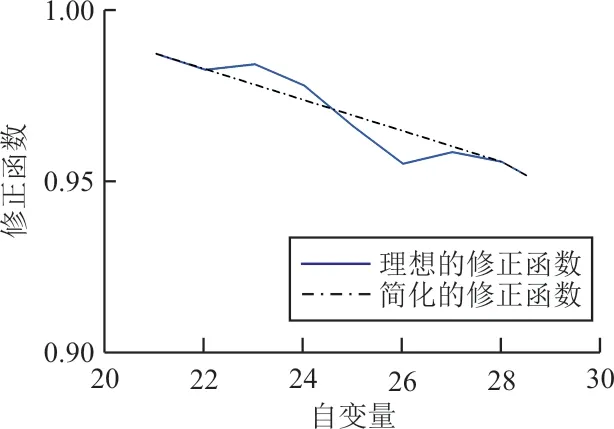
图6 空中段修正函数Fig.6 Modified function in the air segment during takeoff
简化后的修正函数仅需两个关键点数值即可确定:①地面滑跑过程中间时刻的真实速度与仿真速度的比值;②起飞空中阶段到达安全高度(15 m)时刻真实速度与仿真速度的比值。
两个关键点数值通常由该飞机或该飞机改型前飞机试飞试验得到,对于没有试飞试验数据的电动飞机可尝试通过相同布局、质量相近的电动飞机试飞数据统计得到。需要注意的是,如果通过相同布局、质量相近的电动飞机试飞数据确定修正函数,修正后模型的准确性与所选机型密切相关,难以保证准确性,计算结果仅可作为参考。同时,试飞实验前进行起飞性能仿真的精确度要求往往不高,采用近似匀加速模型即可满足精确度要求。
4 算例与分析
4.1 算例参数
本文以某电动飞机增程型号为例,对起飞性能进行仿真计算。根据适航条例要求,在采集飞机起飞距离等数据时,应以最大起飞质量、全油门(电动机最大功率)状态越过15 m障碍物,因此在起飞性能仿真时飞机质量应使用最大起飞质量,电动机应采用最大功率[12]。算例中电动飞机增程型号外形如图7所示,主要参数为:起飞质量600 kg;机翼参考面积12 m2;平均气动弦长0.868 m;电机最大功率40 kW;电机额定功率30 kW;电机效率0.92;控制器效率0.98;地面滑跑摩擦系数0.03。

图7 某电动飞机外形[12]Fig.7 Shape of a certain type of electric airplane[12]
升降舵偏角δz变化时,升力系数、阻力系数和力矩系数的风洞试验数据如图8~图10所示。

图9 阻力系数随迎角的变化Fig.9 Drag coefficient changed with attack angle

图10 力矩系数随迎角的变化Fig.10 Moment coefficient changed with attack angle
螺旋桨的效率、前进比是根据电动飞机螺旋桨的风洞试验获得[22]。不同速度下的螺旋桨效率及前进比如图11所示。

图11 不同速度、不同前进比的螺旋桨效率曲线Fig.11 Propeller efficiency curve changed with different speed and advanced ratio
修正后距离的计算步骤为:
①以风洞实验数据为基础,通过多项式插值得到对应的函数表达式。
②带入数据并采用Runge-Kutta法求解对应阶段的微分方程组,得到对应阶段速度关于时间的函数V(x)。
③通过分析计算该电动飞机增程前原型机起飞加速特性来确定修正函数的两个关键数值:地面滑跑过程中间时刻的真实速度与仿真速度的比值为1.130;起飞空中到达安全高度(15 m)时刻真实速度与仿真速度的比值为0.952。通过这两个关键数值可以得到简化后的修正函数f(t),进而得到修正后的速度Vm(t)。
④使用Simpson数值积分法对Vm(t)的时间求积分可以得到修正后的距离。
4.2 计算结果
模型修正前后仿真结果与试飞采集数据,如表1所示,可以看出:修正前的仿真结果与试飞采集的数据有一定误差,对模型中速度进行修正后仿真结果与试飞试验采集的数据基本吻合,模型准确度高于近似匀加速仿真模型。
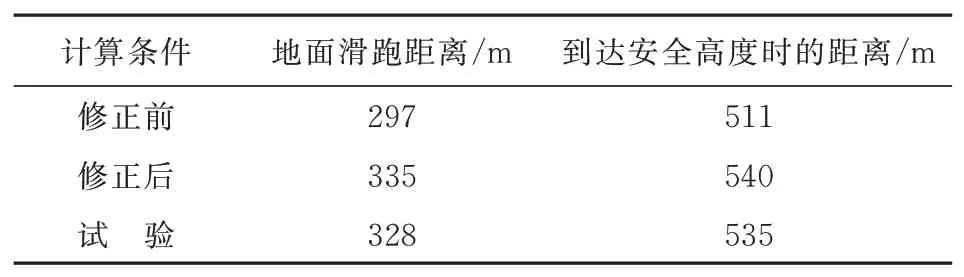
表1 计算结果Table 1 Calculate results
4.3 不同因素对起飞性能影响分析
仿真的意义在于使用仿真模型将特定于某一具体层次的某些不确定性转化为对目标的影响。对于起飞性能仿真而言,需要通过仿真模型尽可能准确地量化如风速、飞机质量等因素对飞机起飞性能的影响。完全通过试验测试不确定因素对起飞性能的影响是不现实的。
以算例中的电动飞机为例,采用修正后的仿真模型分析风速、电动机功率以及飞机质量对起飞性能的影响。
①风速对起飞性能的影响
在其他条件保持不变的情况下,风速从顺风3 m/s变化到逆风3 m/s,规定逆风为正。飞机起飞时风速在小范围内对起飞距离的影响呈线性关系。逆风起飞时,飞机的相对初速度大,有利于起飞。对于本算例中的电动飞机,顺风风速每增加1 m/s,则起飞距离增加5%。
②电机最大功率对起飞性能的影响
算例中的电动飞机电机有两种最大功率40 kW和50 kW,两种不同的功率对应着不同的推力数据。在其他条件保持不变的前提下,分别采用两种不同的最大功率起飞,计算结果如表2所示。

表2 不同最大功率的计算结果Table 2 Calculate results at different maximum powers
从表2可以看出:电机最大功率为50 kW时,起飞距离缩短60 m,约为起飞场长的12%。
③飞机质量对起飞性能的影响
在其他条件保持不变的情况下,飞机起飞质量从520 kg变化到600 kg,距离计算结果如表3所示。

表3 距离计算结果Table 3 Calculation results of distance
从表3可以看出:起飞时飞机质量对起飞距离的影响在小范围内呈线性关系,对于本算例中的电动飞机,质量每增加20 kg,起飞距离增加5%。
研究不同因素对新型号飞机的飞行性能影响,能为电动飞机参数改进提供指导,是电动飞机获取适航型号合格证的重要一环。
5 结论
(1)在小范围内,风速对电动飞机滑跑距离的影响呈线性关系,逆风风速每增加1 m/s,则起飞距离会缩短5%;相较于使用40 kW起飞,电机功率使用50 kW起飞时起飞距离会缩短12%;在小范围内,质量对飞机滑跑距离的影响呈线性关系,电动飞机质量每增加20 kg,起飞距离增加5%。
(2)传统起飞仿真模型与飞机实际起飞过程存在一定差异,这一差异导致仿真结果中起飞距离总是略小于实际起飞距离。根据真实加速特性对模型中速度修正后的仿真模型能比较准确地计算飞机起飞性能,准确性优于传统近似匀加速模型。该模型可以为以后的电动飞机性能研究奠定良好的理论基础。
(3)算例中将起飞地面阶段和起飞空中阶段的修正函数分别设为二次函数形式和一次函数形式,修正后模型仿真结果准确性较高,因此对于算例飞机如此设置修正函数具有一定的可行性。本文修正函数的构建是在某型电动飞机前代机试飞数据拟合的基础上进行的,未必完全适用于其他电动飞机。若要对其他电动飞机起飞性能进行准确计算还需要对其起飞过程中加速特性进行分析。

