短圆管换能器辐射阻抗
梁家宁 莫喜平 柴 勇 刘永平
(1 中国科学院声学研究所 北京 100190)
(2 中国科学院大学 北京 100049)
(3 北京海洋声学装备工程技术研究中心 北京 100190)
0 引言
圆管换能器由于其结构简单、性能可靠、声辐射面积大、辐射效率高等优点,在水声及超声领域有广泛应用。Morse[1]最早研究圆柱体声辐射问题,基于柱坐标系下的声波方程给出了圆柱体辐射声场和格林函数的表达式。Junger 研究了速度在轴向均匀分布以及在轴向和周向周期性变化的无限长圆柱的辐射阻抗[2],并推导了简谐力作用下无限长弹性壳体表面的位移和流体中的声压分布[3]。Robey[4]基于格林函数推导了圆管均匀振动的自辐射和相互辐射阻,并讨论了圆管之间的距离对辐射阻的影响。Greenspon 等[5]研究了无限长刚性圆柱体上矩形活塞的声压和互辐射阻抗,并对平面、球体和圆柱体上的活塞的互辐射阻抗进行了比较。Sandman[6]研究了两端有刚性固定端面支撑的有限长圆柱壳体的辐射阻抗,在计算有限长圆柱壳流体负载时,可以用无限长刚性障柱上的圆柱壳体模型来近似。Steppanishen[7]研究了引入壳理论的弹性圆柱壳辐射阻抗的渐进表达式,并讨论了不同振动模式对声辐射的相互耦合效应。Bulter等[8]建立了刚性扩展模型,利用傅里叶级数法计算了0∼2阶圆管圆周模态的辐射阻抗。当圆管高径比h/r >2时,利用刚性扩展模型可以较好地表述圆管换能器的辐射阻抗,但随着高径比(h/r)的减小,模型计算的辐射阻抗与实际存在较大误差,因此,有必要对短圆管情况下(1h/r2)的辐射阻抗进行更精确的估计。
1 圆管换能器有限元分析
对圆管换能器建立有限元软件二维轴对称模型,如图1所示。换能器为空气背衬,上下两端面处为刚性端盖。为了简化处理,建模过程中忽略刚性端盖和去耦垫,代之以流体介质的刚性边界条件。h为圆管换能器高度,r为圆管换能器半径,在换能器半径方向施加法向振速u。进行谐响应分析,提取表面节点压强p(h),根据公式(1),计算流体反作用力并得到辐射阻抗,分析范围kr= 0.03∼10,结果如图2、图3所示。
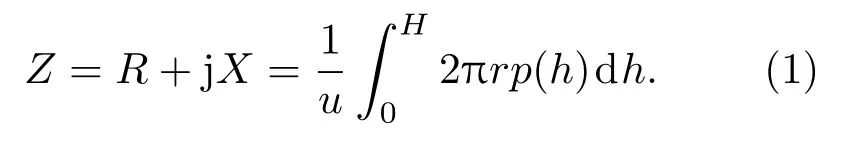
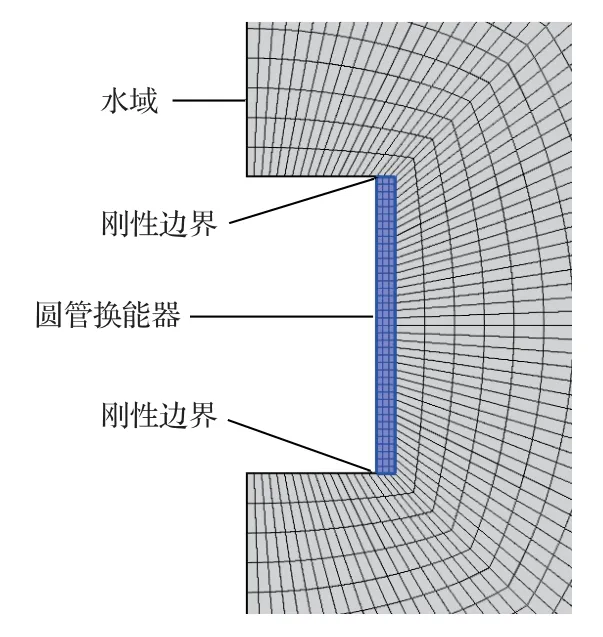
图1 圆管换能器有限元模型Fig.1 Finite element model of a cylindrical transducer
如图2、图3所示,圆管换能器的辐射阻抗与圆管换能器高径比(h/r)有关,且曲线的变化规律较复杂。随着高径比(h/r)的增加,在kr尺度较小时(kr <4),辐射阻抗斜率变大;在kr尺度较大时(kr4),辐射阻抗波动起伏减小。
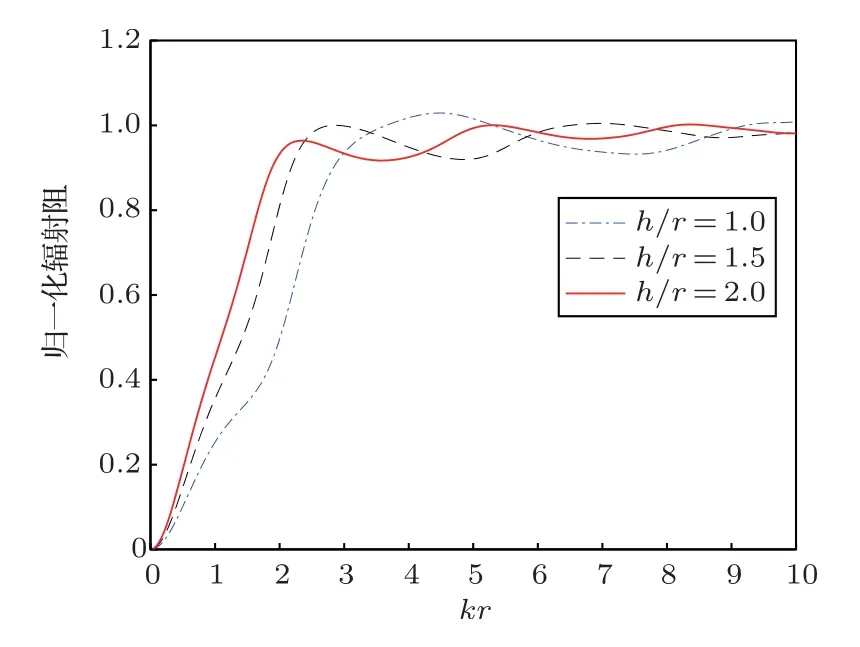
图2 有限元计算辐射阻Fig.2 Finite element calculation results of radiation resistance
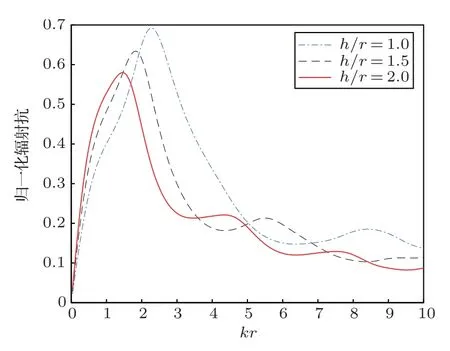
图3 有限元计算辐射抗Fig.3 Finite element calculation results of radiation reactance
2 圆管换能器辐射阻抗的曲线拟合
由于圆管声场瑞利积分求解的复杂性,想直接得到圆管换能器辐射阻抗的解析解是很困难的[9−10]。因此,提出一种圆管辐射阻抗经验公式的表达形式。为了确定经验公式的母函数形式,仔细研究图2、图3中曲线,发现其具有以下特点:(1)辐射阻抗受两因素影响,分别是圆管的高径比(h/r)和波数k。因此,母函数中应带有两自变量;(2)曲线存在渐进特性,辐射阻的渐进值R∞=ρcS,辐射抗的渐进值X∞= 0;(3)曲线存在振荡特性,且振荡幅度呈衰减规律;(4)曲线在kr较小时的增长趋势类似于脉动球源的辐射阻抗曲线。
根据以上特点,选择处理方法和函数类型:(1)设经验公式的两自变量为kh、kr;(2)渐进特性:将参量减去渐进值,作为新变量参与曲线拟合;(3)振荡特性及衰减规律:用sinc 函数进行拟合;(4)设定母函数时参考脉动球源辐射阻抗公式。
(1)归一化辐射阻经验公式为
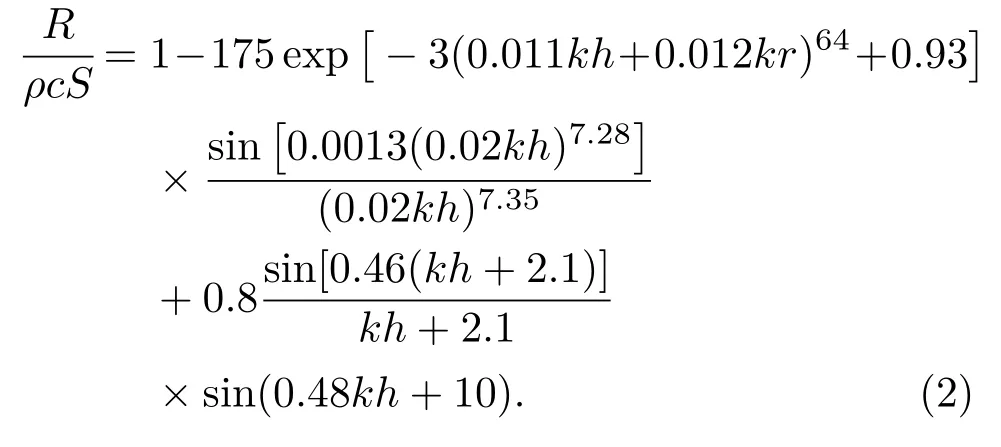
(2)归一化辐射抗经验公式为
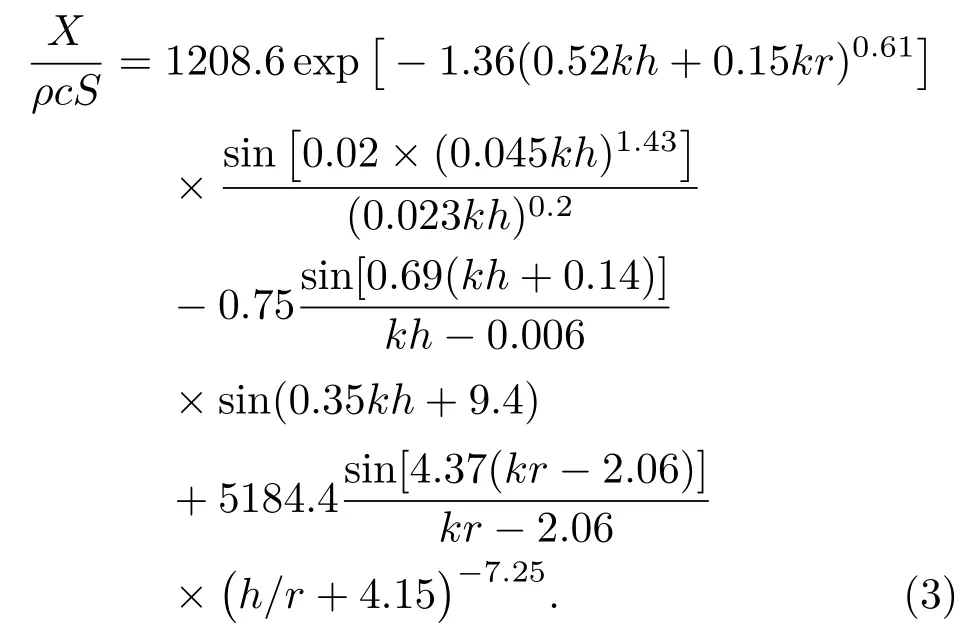
3 辐射阻抗经验公式模型有效性验证
为了估计圆管换能器辐射阻抗,Bulter 提出了圆管刚性扩展模型。声场的瑞利积分可近似考虑成傅里叶级数的叠加,得到的辐射阻抗公式为[8]

其中,βm=k[1−(m/M)2]1/2,M=d/λ,d为间距。
下面,选取高径比h/r=1、h/r=1.5、h/r=2三组数据对比分析经验公式与刚性扩展模型计算辐射阻抗结果。
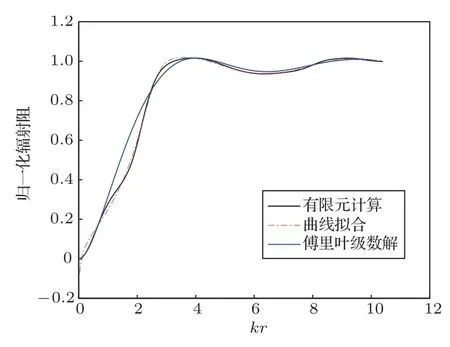
图4 h/r =1,辐射阻计算方法对比Fig.4 Comparison of radiation resistance calculation results when h/r =1

图5 h/r =1,辐射抗计算方法对比Fig.5 Comparison of radiation reactance calculation results when h/r =1
由图4∼图9对比可以看出,在1h/r2 的范围内,经验公式计算得到的辐射阻抗与有限元结果较为相符,拟合程度较高。随后计算曲线拟合、傅里叶级数解与有限元计算得到的辐射阻抗的拟合系数,如表1、表2所示。曲线拟合的拟合系数在3种高径比情况下均大于0.998,而傅里叶级数解拟合系数均不超过0.99,这是由于刚性扩展模型为理想模型,在较低高径比下存在刚性壁面的反射,导致计算结果与有限元结果出现误差。
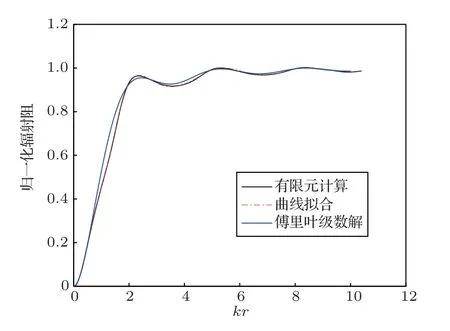
图6 h/r =1.5,辐射阻计算方法对比Fig.6 Comparison of radiation resistance calculation results when h/r =1.5
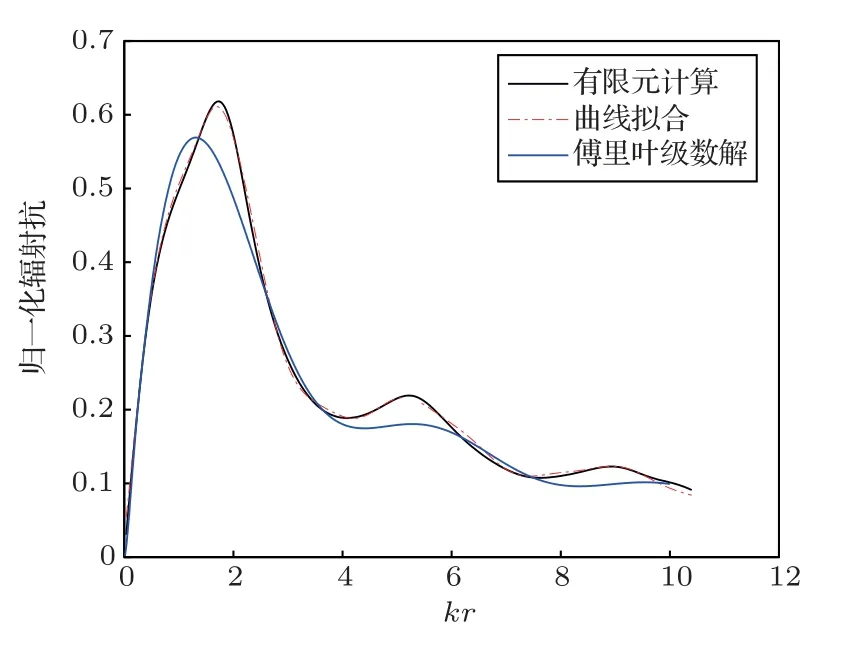
图7 h/r =1.5,辐射抗计算方法对比Fig.7 Comparison of radiation reactance calculation results when h/r =1.5
表1 曲线拟合、傅里叶级数解与有限元计算辐射阻的拟合系数(1 h/r 2)Table 1 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(1 h/r 2)
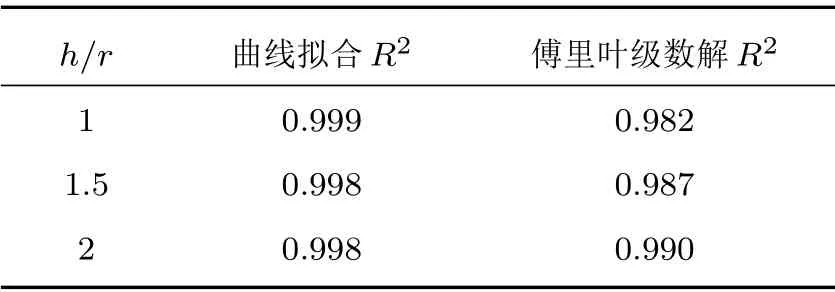
表1 曲线拟合、傅里叶级数解与有限元计算辐射阻的拟合系数(1 h/r 2)Table 1 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(1 h/r 2)
h/r 曲线拟合R2 傅里叶级数解R2 0.999 0.982 1.5 0.998 0.987 2 0.998 0.990 1
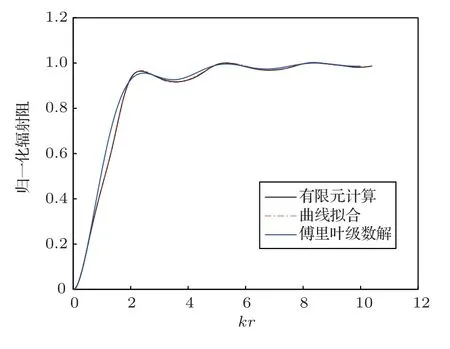
图8 h/r =2,辐射阻计算方法对比Fig.8 Comparison of radiation resistance calculation results when h/r =2
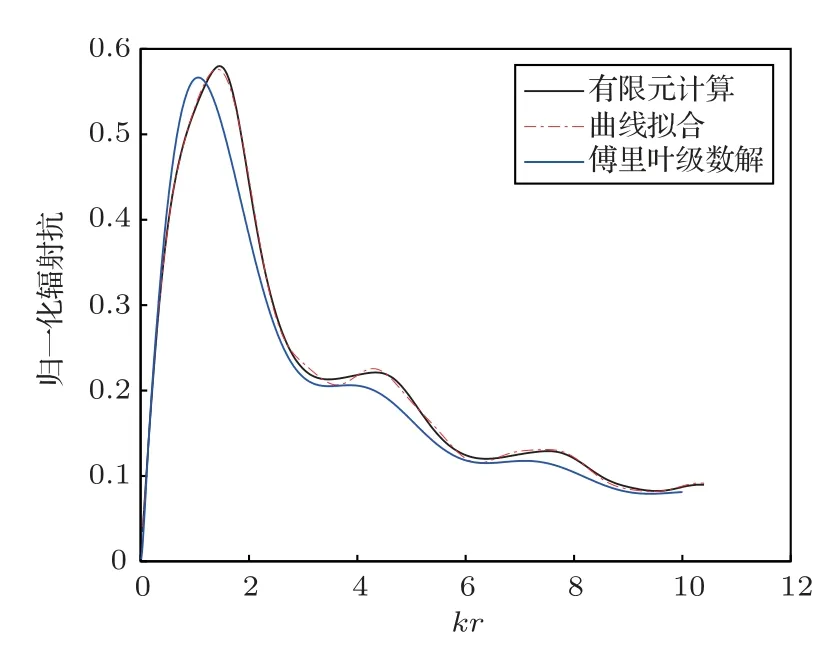
图9 h/r =2,辐射抗计算方法对比Fig.9 Comparison of radiation reactance calculation results when h/r =2
表2 曲线拟合、傅里叶级数解与有限元计算辐射抗的拟合系数(1 h/r 2)Table 2 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(1 h/r 2)
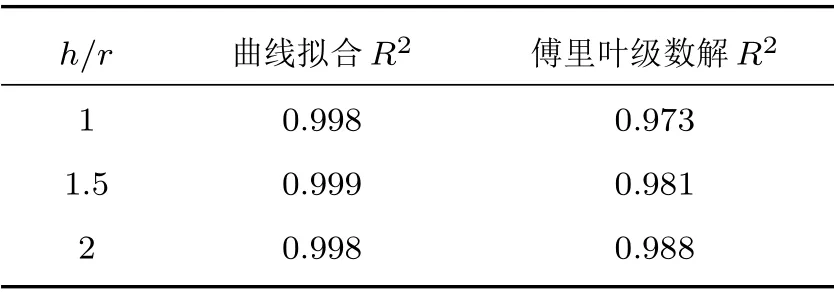
表2 曲线拟合、傅里叶级数解与有限元计算辐射抗的拟合系数(1 h/r 2)Table 2 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(1 h/r 2)
h/r 曲线拟合R2 傅里叶级数解R2 0.998 0.973 1.5 0.999 0.981 2 0.998 0.988 1
当圆管高径比进一步减小时(0.8h/r1),计算曲线拟合、傅里叶级数解与有限元计算得到的辐射阻抗的拟合系数,如表3、表4所示。随着圆管高径比的不断减小,经验公式模型与有限元计算结果误差逐渐增大。曲线拟合的拟合系数在两种高径比情况下相较之前略有降低,但仍大于0.994,这是由于为了保证经验公式的计算精度,h/r1 部分的数据未参与经验公式拟合。然而当0.8h/r1时,傅里叶级数解拟合系数均小于0.98,计算结果与理论值相差较大。此时经验公式相较于刚性扩展模型仍能较准确描述圆管换能器辐射阻抗。
表3 曲线拟合、傅里叶级数解与有限元计算辐射阻的拟合系数(0.8 h/r 1)Table 3 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(0.8 h/r 1)

表3 曲线拟合、傅里叶级数解与有限元计算辐射阻的拟合系数(0.8 h/r 1)Table 3 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation resistance(0.8 h/r 1)
h/r 曲线拟合R2 傅里叶级数解R2 0.8 0.994 0.973 0.9 0.996 0.978
表4 曲线拟合、傅里叶级数解与有限元计算辐射抗的拟合系数(0.8 h/r 1)Table 4 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(0.8 h/r 1)

表4 曲线拟合、傅里叶级数解与有限元计算辐射抗的拟合系数(0.8 h/r 1)Table 4 Fitting parameters between curve fitting, Fourier series solution and finite element calculation of radiation reactance(0.8 h/r 1)
h/r 曲线拟合R2 傅里叶级数解R2 0.8 0.998 0.967 0.9 0.998 0.970
4 结论
由于圆管换能器的辐射阻抗随圆管半径、高度和波数而变化,因此辐射声场很难用解析解表达。为解决这一问题,采用有限元分析法计算了圆管换能器的辐射阻抗,并根据计算结果拟合得到了经验公式。通过将刚性扩展模型和经验公式模型的结果与有限元数据进行比较,可以确定当短圆管情况下(1h/r2),经验模型的精度在误差允许范围内。同时,当圆管高径比在0.8∼1范围内,经验公式只存在较小的误差。因此,当圆管换能器的高径比较小时,经验公式模型可以更准确地描述辐射阻抗。这不仅有助于研究圆管换能器的辐射功率和效率,而且有助于进一步优化结构。同时,为类似难以用解析解表达的问题提供借鉴思路。

