北斗三号全球导航卫星系统全球广播电离层延迟修正模型(BDGIM)应用性能评估

袁运斌，李 敏，霍星亮，李子申，王宁波

1. 中国科学院精密测量科学与技术究创新研究院，湖北 武汉 430077； 2. 大地测量与地球动力学国家重点实验室，湖北 武汉 430077； 3. 中国科学院光电研究院，北京 100094

电离层是影响全球卫星导航系统服务性能最棘手的误差源之一[1]。为满足广大单频导航定位用户对电离层延迟实时修正的需求，美国GPS、欧盟Galileo和中国北斗(BDS)在其广播星历中播发了电离层模型参数[2]。美国GPS系统和欧盟Galileo系统分别采用8参数的Klobuchar模型[3](GPSklob)和NeQuick模型提供全球电离层修正服务[4]。我国的北斗二号系统采用改进的8参数Klobuchar模型(BDSklob)提供覆盖亚太地区的电离层修正服务[5-6]。北斗三号全球导航卫星系统(下称“北斗三号系统”)采用自主设计研制的北斗全球广播电离层延迟修正模型(BeiDou global broadcast ionospheric delay correction model，BDGIM)[7-9]。北斗三号系统实时地播发9个BDGIM模型参数，为全球用户提供实时电离层修正服务。

系统深入地评估和分析北斗三号全球广播电离层延迟改正模型的修正效果，不仅可为北斗全球系统的用户使用电离层修正服务提供参考，还可有效保障和改善刚开通服务的北斗三号系统广播电离层改正性能提供科学依据。以往，针对GPSklob、NeQuick和BDSklob模型，国内外学者开展了大量的精度评估工作[6,10-14]。研究表明，GPSklob模型在全球中纬度地区可以实现50%左右的电离层延迟修正精度[3]，NeQuick模型在全球可以实现54%～65%的修正精度[15]，BDSklob在北半球中纬度区域可实现70%左右的修正精度[11]。

近年来，随着北斗三号系统的快速建设与发展，对于BDGIM模型的性能评估逐渐受到研究者的关注[16-28]。研究结果表明：BDGIM模型在中国区域、北半球中低纬区域及全球，分别可以实现80.9%[8]、75%[6]和77.2%[22]的修正精度；在全球范围内BDGIM模型性能相对于BDSklob均有所提升，尤其在高纬地区提升范围在20%[24]；采用BDGIM模型获取的单频伪距定位精度较BDSklob和GPSklob模型的同类定位精度可分别提高13%和7%～10%[23]。然而，现有关于BDGIM模型的精度评估主要是基于2019年以前特别是北斗三号系统建设初期在5颗BDS-3试验卫星播发的BDGIM模型参数开展的。随着北斗三号系统于2020年6月完成全部组网卫星发射并正式开启全球服务，BDGIM模型在北斗三号全球组网完成前后的改正精度及对用户测距定位影响需进一步分析与研究。

本文在介绍和阐述BDGIM模型计算方法的基础上，通过以国际GNSS服务(International GNSS Service,IGS)发布的高精度全球电离层格网(GIM)产品和GNSS跟踪站实测电离层TEC(total electron content)为参考，分析电离层延迟改正精度、标准单点定位(standard point positioning,SPP)以及比较BDGIM模型的发播参数与欧洲定轨中心(The Center for Orbit Determination in Europe,CODE)发播参数之间的差异等多种方式，分析和研究了BDGIM模型在中国区域、亚太地区(60°E—160°E、60°N—60°S)以及全球范围的改正精度等应用性能，并与GPSklob模型和BDSklob模型进行了对比分析。

1 北斗三号全球广播电离层延迟改正模型(BDGIM)及其特点

BDGIM模型包括发播项和非发播项参数，其中发播项为9个模型参数，而非发播项的参数信息则固化于用户接收机端。BDGIM模型的数学结构可以表达为[7-8]

(1)

式中，Tion表示卫星与接收机视线方向的电离层延迟改正值，单位为m；mf表示电离层投影函数，用于垂向TEC(VTEC，Iv)和斜向电离层TEC(STEC)之间的转换，其计算公式见式(2)；f表示当前信号对应的载波频率；αi(i=1～9)表示BDGIM模型的播发参数，由区域/全球北斗监测站数据计算得到，单位为TECU；Ai(i=1～9)表示根据电离层穿刺点位置及观测时刻计算得到的数值，其计算公式见式(3)；N0表示电离层延迟预报值，由固化于用户接收机端的预报系数、电离层穿刺点位置及观测时刻计算得到，单位为TECU，其计算公式为

(2)

式中，mf表示余弦函数投影函数；R表示地球半径，取值为6378 km；Hion表示电离层薄层高度，取值为400 km；Z′表示电离层穿刺点处的卫星天顶距；Z表示接收机位置处的卫星天顶距。

(3)

式中，φ′及λ′分别表示日固系下电离层穿刺点处的地磁纬度和地磁经度，单位为rad；ni及mi(i=1～9)分别表示第i个播发参数对应的球谐函数阶次；Nni,mi表示正则化函数，计算公式见(4)(式中m=0时，δ0,m的值为1；m>0时，δ0,m的值为0)；Pni,mi表示标准勒让德函数，计算公式见式(5)(式中n、m均取绝对值)。

(4)

(5)

(6)

式中，βj表示BDGIM模型的非播发参数，由一系列预报系数计算得到，其计算公式见式(7)；nj与mj分别表示第j个非播发参数对应的球谐函数阶次；Nnj,mj表示正则化函数，Pnj,mj表示标准勒让德函数，其计算公式分别参见式(4)及式(5)

(7)

式中，Tk表示各非播发参数对应的预报周期；ak,j及bk,j表示BDGIM模型的非发播系数，单位为TECU；tk表示对应当天约化儒略日的奇数整点时刻(01:00:00，03:00:00，05:00:00，…,23:00:00)，单位为d，用户计算时选取距离当前计算时刻最近的一组参数即可，无须重复计算。

此外，为避免BDGIM模型计算的Iv出现负值，Iv最小值建议按式(8)计算

(8)

总体上，BDGIM模型的主要特点可概括为以下几方面：①模型以球谐函数为基础，球谐函数是描述全球高精度电离层TEC时空变化较优的数学模型之一。②模型根据不同球谐系数对电离层TEC计算贡献的大小将球谐函数系数分为播发参数和非播发参数两类，通过这种方式，模型既减少了电离层球谐函数播发参数个数，同时通过对选取的非播发参数进行建模预报，尽可能保留了高阶次球谐系数对全球电离层TEC空间分辨率的贡献，确保了采用的球谐函数对全球电离层TEC的精确描述能力。③BDGIM模型通过引入设计合理的背景电离层信息，基于境内监测站及少量境外监测站观测数据实现了模型播发参数的更新计算，尽可能地解决了一定时期内BDS进行海外监测站引发的问题。

用户接收机采用BDGIM模型计算电离层延迟，包含电离层穿刺点位置计算、基于播发系数的电离层延迟计算值解算、基于非发播系数的电离层延迟预报值计算、穿刺点处垂直方向电离层延迟计算、穿刺点电离层投影函数计算以及信号传播路径上电离层延迟改正值计算共6个环节。具体计算步骤参考文献[7—8]。

2 BDGIM模型电离层延迟改正精度评估方法

2.1 模型评估方法

本文将IGS发布的最终GIM产品、GNSS跟踪站(后文统称为“检测站”)实测BDS和GPS数据获取的TEC以及CODE发布的球谐系数为参考，从多个角度分析北斗三号系统组网完成前后(2020年5月1日—2020年7月20日)这一时段内BDGIM模型在全球不同地区的电离层延迟改正精度及其BDS单频SPP应用效果。

(1) BDGIM模型TEC与IGS发布的最终GIM TEC产品对比。IGS发布的最终GIM产品是根据不同国际电离层分析中心提供的GIM产品通过加权得到的，其精度为2～8 TECU，是目前国际发布的最具代表性、精度与可靠性较稳定的全球电离层TEC格网产品[29-30]。本文将以IGS发布的最终GIM产品为参考，按照IGSGIM产品的时空分辨率计算所有格网点TEC值，进而分析和研究BDGIM模型的电离层延迟改正精度。

(2) BDGIM模型TEC与BDS和GPS实测TEC对比。基于选取的GNSS检测站的实测BDS和GPS双频数据可以计算各卫星穿刺点的电离层VTEC信息，利用BDGIM模型也可获得穿刺点处的VTEC模型计算值。通过对比和研究二者差异可以较准确地分析和评估BDGIM模型的电离层延迟修正精度。在实测TEC计算质量得到保障的前提下，这种对比方法相对更加准确。基于GPS和BDS双频数据提取电离层TEC过程中，本文采用中国科学院精密测量科学与技术创新研究院IGMAS分析中心提供的相关产品进行卫星和接收机差分码偏差(DCB)修正。

(3) BDGIM模型对北斗定位精度的影响评估。对于单频卫星导航用户，通常采用广播电离层改正模型实时控制与削弱电离层延迟对导航定位结果的影响。为评估和掌握BDGIM模型在定位中的应用效果，利用MGEX跟踪站北斗全球观测数据进行单频SPP，评估BDGIM模型对北斗定位的影响。

为全面对比分析和了解BDGIM模型与其他广播电离层模型的改正精度等应用服务性能，本文也对GPSklob模型和BDSklob电离层模型进行了评估与分析，并系统分析和研究了不同电离层模型对各检测站BDS单频SPP定位精度的影响。

(4) BDGIM模型发播参数与CODE发布的球谐系数对比。采用球谐函数模型拟合全球电离层TEC时，球谐函数的阶次代表电离层TEC在全球范围内的分辨率，不同阶次的系数代表着不同频率信号对合成信号的贡献大小，其中全球电离层TEC的平均值可以由第一项球谐系数表示[31]。BDGIM模型与CODE均采用球谐函数作为TEC拟合函数，二者区别在于采用的球谐阶次和系数的更新时间。BDGIM采用9个球谐系数，每2 h更新一组，CODE采用阶次为15阶×15阶的球谐系数，每1 h更新一组。通过对比BDGIM模型发播参数与CODE发布的球谐系数，可以一定程度地了解BDGIM对全球电离层TEC的总体描述能力。

2.2 主要精度评定指标

目前，通常使用的电离层时延模型改正精度的评价指标，主要包括不同电离层模型的TEC计算值与电离层TEC参考值之间的平均偏差(bias)、均方根(RMS)及修正百分比(PER) 3种，具体计算见式(9)。其中，bias与RMS分别表示基于电离层时延修正模型计算的电离层TEC与参考电离层TEC差值的平均值及均方根；PER表示电离层时延修正模型相对于电离层TEC参考值的修正百分比。bias与RMS为绝对精度指标，PER为相对精度指标。

(9)

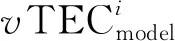
从上述定义可知，当TEC参考值较大时，即使相对精度指标较高，其绝对的误差量值也可能较大；当TEC参考值较小时，即使其相对精度较低，但其绝对误差量值也可能较小。同时，电离层受太阳活动影响表现出明显的周年变化特征，如在一个太阳活动周年内(约11 a)TEC的最大值与最小值相差10倍左右，在不同太阳活动水平下绝对精度指标和相对精度指标大小所体现的效果可能会存在一定的差异。总体而言，在电离层活动高年，相对精度指标较高，绝对精度指标往往会偏低，而在电离层活动低年，相对精度指标较小，绝对精度指标往往会偏高。因此，有些时段难以采用单一的精度指标描述电离层时延修正精度。在实际评估时，通常需综合利用绝对指标与相对指标并基于较长时段的数据分析和研究电离层模型在不同太阳活动水平下的应用效果，实现更为精准合理的精度等性能评估。

2.3 试验数据

结合上文中精度分析和评估方法的需要，选取2020年DOY 122—DOY 202作为分析与研究北斗三号组网前后全球电离层延迟广播改正精度等应用性能的时间段。利用这一时段内IGS GIM产品及多频多模GNSS试验跟踪网(MGEX)83个GNSS检测站采集的观测数据开展试验分析与评估。图1给出了所选GNSS检测站的分布情况。可以看出，选取的GNSS检测站基本覆盖了全球高中低纬度，能够反映不同电离层模型在全球各地区的整体修正精度。为综合评估不同广播电离层模型在不同区域的修正效果，本文将按照中国区域、亚太地区以及全球范围分开进行改正精度的统计。

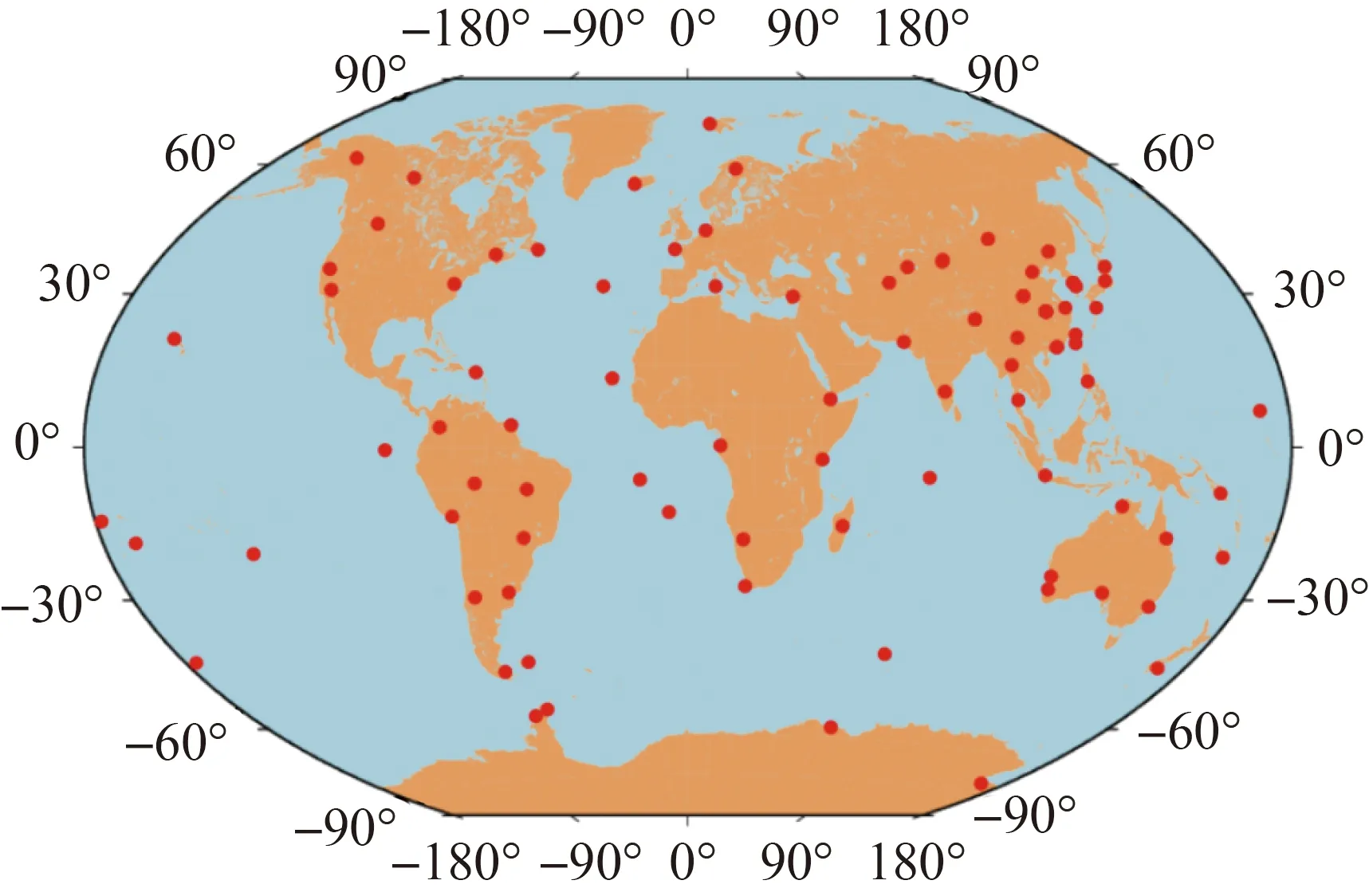
图1 选取的全球GNSS检测站分布Fig.1 Distribution of the selected GNSS checking stations

3 评估结果

3.1 BDGIM模型TEC与IGS GIM TEC产品对比

图2和图3分别给出了2020年DOY 122—DOY 202期间BDGIM模型中国区域、亚太地区以及全球范围内的RMS和PER随时间的变化，表1和表2分别给出了北斗三号系统组网完成前后的平均精度统计结果。可以看出，在2020年北斗三号系统完成全球组网(175 d)后，BDGIM精度没有发生显著变化，BDSklob优化了模型参数解算策略导致其在亚太地区和全球范围的精度有了较为明显提升。在中国区域、亚太地区和全球范围内，以IGS GIM提供的TEC为参考，BDGIM模型在北斗三号系统组网完成前后的平均电离层修正百分比分别达到84.45%、74.74%和64.57%，相对于GPSklob模型分别提升约为16.98%、26.14%和20.54%。以IGS GIM为参考，BDGIM模型精度在全球不同区域均优于GPSklob和BDSklob模型。除在中国区域BDSklob的修正精度略优于GPSklob模型之外，在其他地区GPSklob模型平均精度均优于BDSklob模型。

表1 2020年DOY 122—DOY 175以IGS GIM为参考的不同电离层模型精度统计

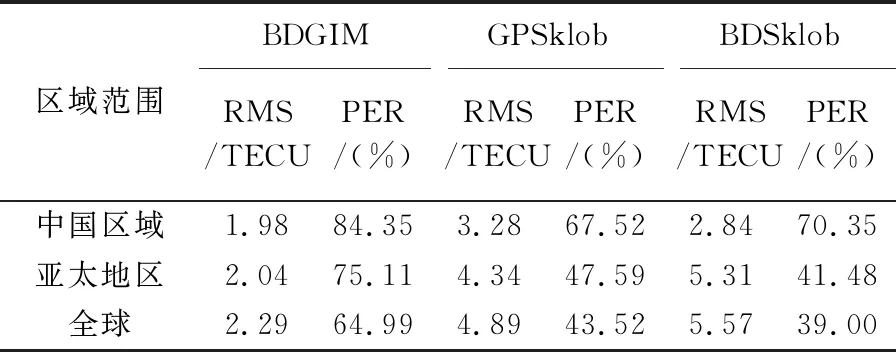
表2 2020年DOY 176—DOY 202以IGS GIM为参考的不同电离层模型精度统计

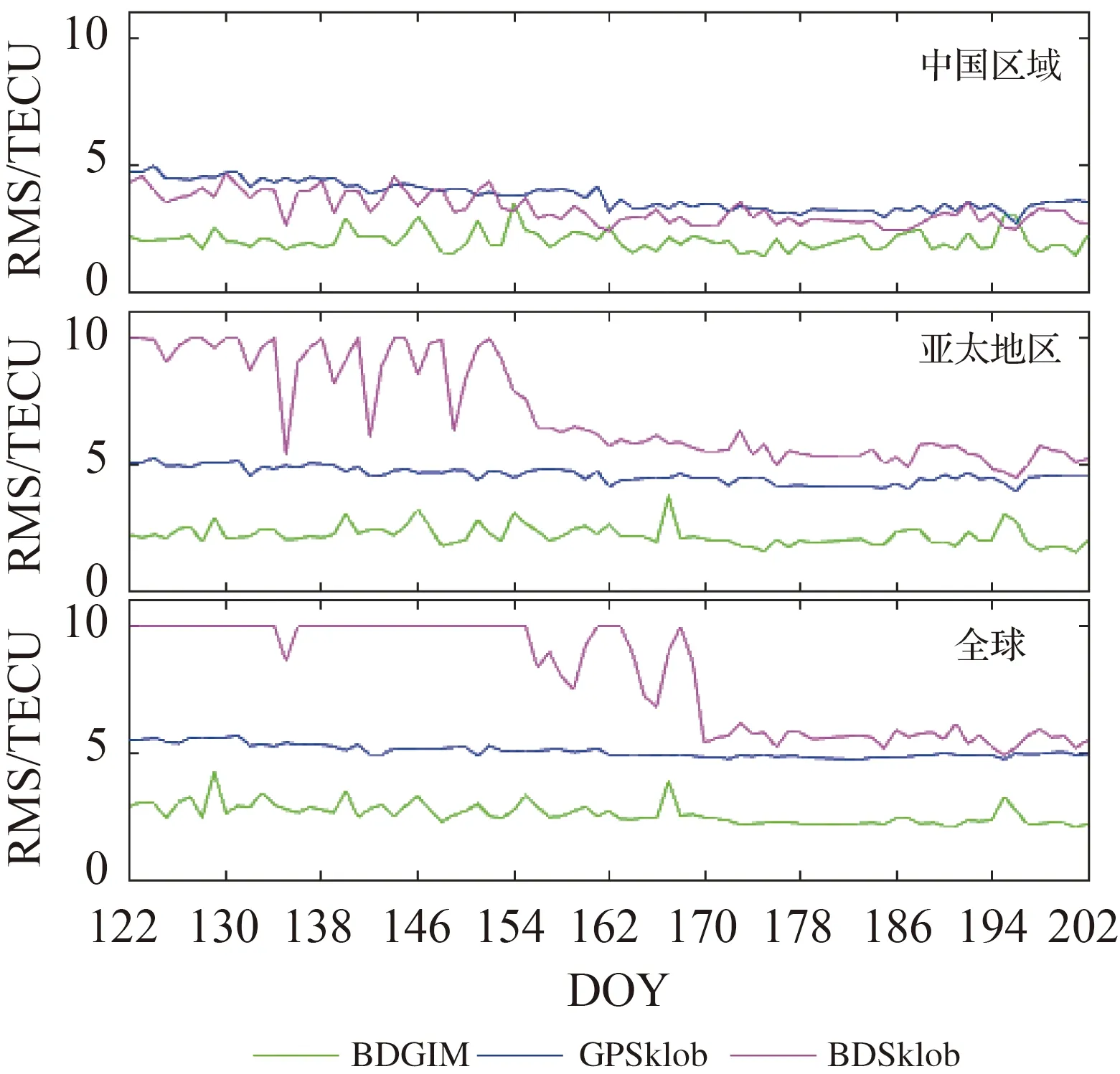
图2 2020年DOY 122—DOY 202不同电离层模型TEC计算值与IGSGIM相比的RMS时间序列Fig.2 Time series of the RMS of the TEC differences betweenmodel estimates and the IGSGIM during the period from DOY 122 to DOY 202 in 2020

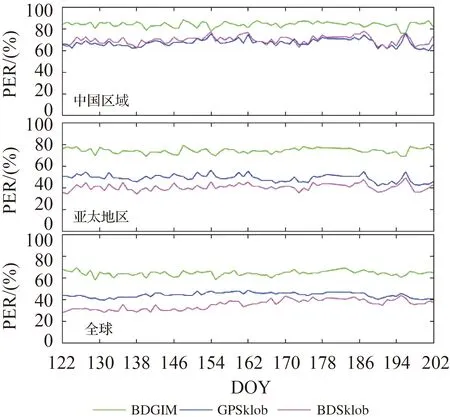
图3 2020年DOY 122—DOY 202以IGSGIM为参考的不同电离层模型修正百分比时间序列Fig.3 Correction percentage time series of TEC models with respect to the IGSGIM during the period from DOY 122 to DOY 202 in 2020

为进一步了解BDGIM模型在全球不同纬度带的精度情况，表3对DOY 122—DOY 202不同纬度带的TEC均值及模型精度进行了统计。BDGIM模型在全球中、低、高纬度的RMS精度分别优于2.2、2.5和2.94 TECU。从相对精度指标来看，BDGIM模型在北半球中纬度和低纬度地区精度较高，其修正百分比分别为81.3%和80.8%；在南半球低纬度地区BDGIM模型修正百分比为73.5%；在以海洋为主的南半球中、 高纬地区，BDGIM模型的修正百分比相对较低。一方面，类似GPSklob模型，BDGIM模型主要服务区域也是人类生产和生活比较集中的中纬度及其附近区域(也是单频用户比较集中的区域)；按设计要求，其模型系数主要采用中国境内为主结合少数布设于境外的为数不多的北斗三号运控站(必须注意的是，到目前为止，只有国内运控站参与了BDGIM播发参数的计算)数据计算得到(由于地理因素，这些站大部分布设在北半球)，加之，用于计算9个播发参数的背景电离层约束信息主要是利用北半球资料为主建立的，使得BDGIM模型在北半球中低纬度修正精度通常要显著优于其他区域。另一方面，2020年属于太阳活动低年，全球特别是南半球中、高纬度地区电离层TEC绝对值较小，导致BDGIM模型在这两个纬度带修正百分比显得相对较低，这与2.1节所述的精度指标表现形式是一致的；而实际上，其相应的RMS指标数值大概在2.94 TECU，通常要小于电离层活动高年的数值，其实际的定位精度也往往更高，即使不进行电离层修正，其定位精度也可能达到甚至优于电离层活动高年的水平。

以2020年DOY 200 18:00(UTC)时刻为例，图4和图5分别给出了不同模型计算的全球电离层TEC及其与IGSGIM产品差异的全球分布情况。可以看出，BDGIM模型与IGSGIM产品呈现的全球电离层TEC分布最为相近，能够精细表达赤道及低纬度地区的电离层TEC分布。GPSklob和BDSklob模型只能近似给出TEC的分布情况，无法反映夜间TEC形态的变化，这是由Klobuchar模型将夜间电离层设置为常数值造成的。与BDSklob模型和GPSklob相比，BDGIM模型TEC与IGSGIM TEC产品之间的差异最小且在全球分布较为均匀，最大差异分布在南半球高纬度海洋区域。与GPSklob模型相比，BDSklob模型计算的TEC呈现南北半球对称分布的特征，且在中国区域具有更高精度，但在南半球特别是高纬度区域精度较差，其原因在于BDSklob模型参数主要由中国境内的跟踪站数据计算获得，而在计算南半球电离层TEC时是采用与北半球对称的方式计算得到，因而更适合于中国区域。该现象与文献[11]得出的BDSklob模型在高纬地区应用效果的结论一致。

图4 不同电离层模型计算的全球TEC分布Fig.4 Distribution of global TEC calculated by different ionospheric models

图5 不同电离层模型计算的TEC与IGSGIM产品的差异Fig.5 Distribution of the differences of the TEC estimates obtained from different ionospheric models and those from IGSGIM

表3 2020年DOY 122—DOY 202以IGS GIM为参考的BDGIM电离层模型在各纬度带精度统计

3.2 BDGIM模型TEC与BDS和GPS实测TEC对比

利用选取的83个检测站实测BDS和GPS数据获取的电离层TEC，评估BDGIM模型的修正精度。图6给出了2020年DOY 122不同电离层模型在全球各检测站TEC计算值与实测TEC相比的RMS值。IGSGIM、BDGIM、GPSklob及BDSklob在中国区域的电离层延迟改正精度分别为2.73、2.70、4.82和4.52 TECU，在亚太地区的电离层延迟改正精度分别为2.58、2.62、4.85和5.14 TECU。可以看出，除IGSGIM产品外，BDGIM模型计算的电离层TEC在与选取的各全球检测站计算的电离层TEC的差值的RMS均最小，明显小于GPSklob模型和BDSklob模型相应的同类计算结果。

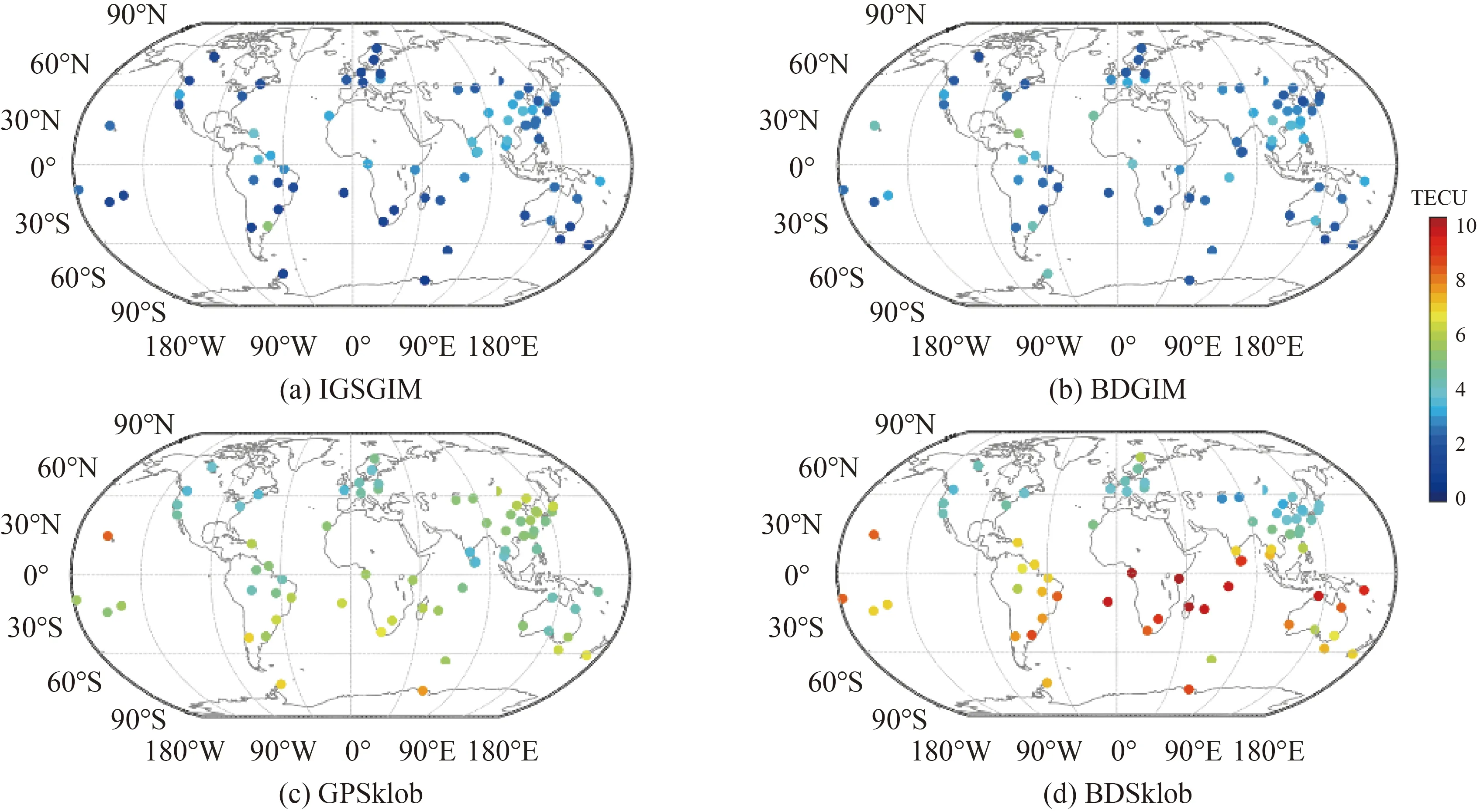
图6 2020年DOY 200不同电离层模型在各检测站的计算值与实测TEC对比的RMSFig.6 RMS of the differences between model TEC estimates and the measured TEC on DOY 200 in 2020

图7和图8分别给出了2020年DOY 122—DOY 202这一时段不同电离层模型在不同区域的RMS和相对修正精度随地方时的变化情况。表4和表5给出了北斗三号系统组网完成前后不同模型日精度的平均统计结果。由上述图、表可见，BDGIM和IGSGIM精度在白天和夜间没有显著差异，BDSklob和GPSklob模型在夜间精度明显低于白天。由表4和表5可知，在2020年北斗三号系统完成全球组网(DOY 175)后，BDGIM模型PER精度没有发生显著变化。在北斗三号系统组网完成前后，BDGIM在中国区域、亚太地区及全球各检测站的平均电离层延迟修正精度分别为73.12%、70.18%和68.06%，明显优于BDSklob和GPSklob模型的修正精度。

图7 2020年DOY 122—DOY 202不同电离层模型TEC计算值与实测TEC相比的RMS随地方时变化Fig.7 RMS of the differences between model TEC estimates and the measured TEC at different local time bins during the period from DOY 122 to DOY 202 in 2020

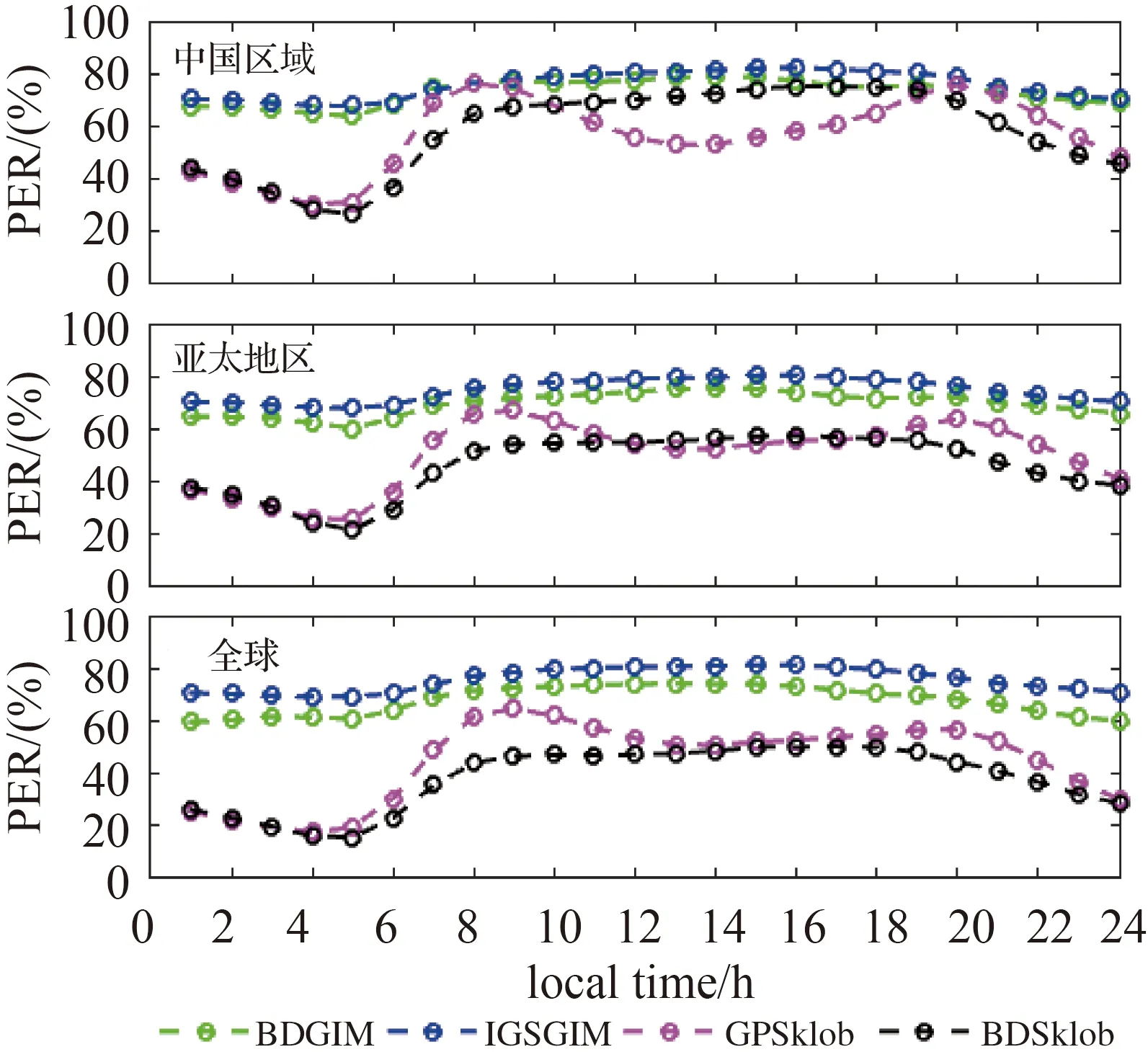
图8 2020年DOY 122—DOY 202不同电离层模型TEC计算值与实测TEC相比的电离层修正百分比随地方时变化Fig.8 The correction percentage for model TEC estimates with respect to the measured TEC at different local time bins during the period from DOY 122 to DOY 202 in 2020

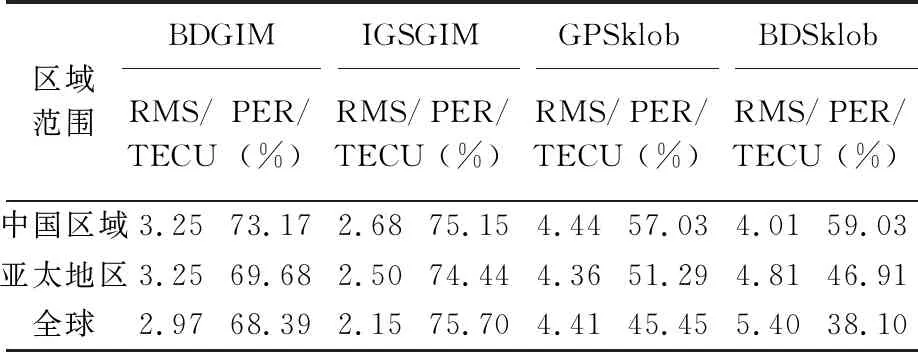
表4 2020年DOY 122—DOY 175不同电离层模型TEC计算值与实测TEC相比平均精度统计

表5 2020年DOY 176—DOY 202不同电离层模型TEC计算值与实测TEC相比平均精度统计

3.3 BDGIM模型对北斗定位精度影响的分析

从前文分析可知，BDGIM模型在北斗三号系统全球组网完成前后精度没有发生显著变化，因此，本节在分析BDGIM模型对北斗定位精度影响时不再对北斗三号系统全球组网完成前后的结果进行对比。以2020年DOY 122北半球中纬度测站POL2和南半球低纬度测站TOW2测站为例，对北斗用户采用BDGIM模型的单频SPP定位结果作进一步分析。图9和图10给出了两个测站在水平和高程方向上的定位误差时间序列图。图11给出了定位精度统计结果。从图9、图10可以看出，采用不同电离层模型的定位结果差异主要体现在高程方向上。在POL2站，BDGIM和BDSklob模型优于GPSklob模型，在高程上的定位精度分别比GPSklob模型提升了0.57和0.39 m。在TOW2站，使用BDGIM模型的定位精度较GPSklob模型在高程方向提高了0.51 m，而使用BDSklob模型获得的定位精度相对低一些。

图9 2020年DOY 122 POL2站定位精度时间序列Fig.9 Time series of the accuracy of BDS SPP at station POL2 on DOY 122 in 2020

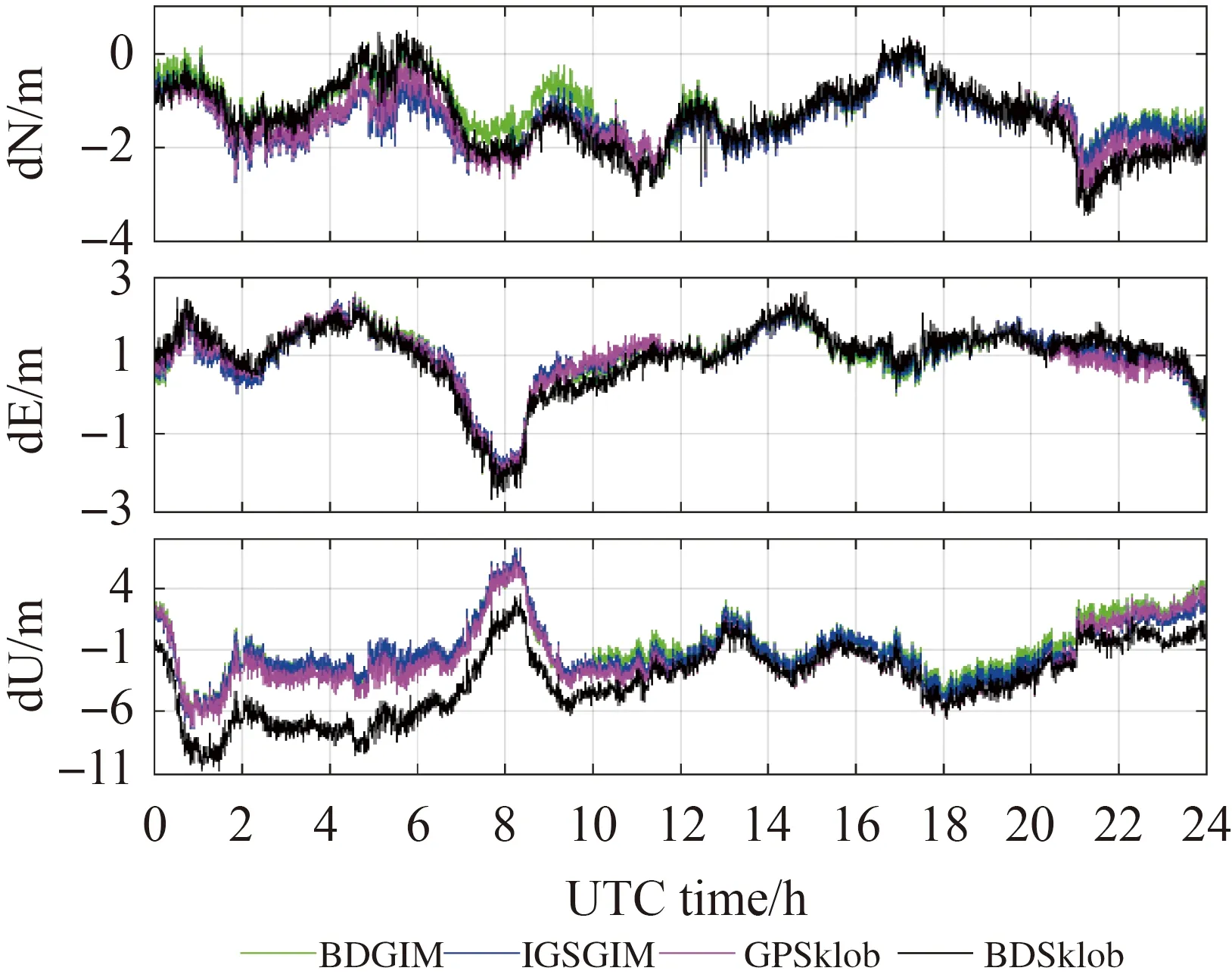
图10 2020年DOY 122 TOW2站定位精度时间序列Fig.10 Time series of the accuracy of BDS SPP at station TOW2 on DOY 122 in 2020

图11 2020年DOY 122 POL2和TOW2测站BDS SPP定位精度Fig.11 BDS SPP accuracy at stations POL2 and TOW2

图12给出了2020年DOY 122—128不同电离层模型在选取的各全球检测站三维位置定位误差的RMS时间序列。表6给出了选取的各检测站平均定位精度统计结果。由上述图、表可以看出，采用BDGIM模型的定位精度总体上(在大多数时间)优于GPSklob及BDSklob模型。与采用GPSklob模型和BDSklob模型的单频SPP结果相比，BDGIM模型的应用使中国区域定位精度分别提高0.25及0.16 m和亚太地区定位精度分别提高0.16及0.37 m。

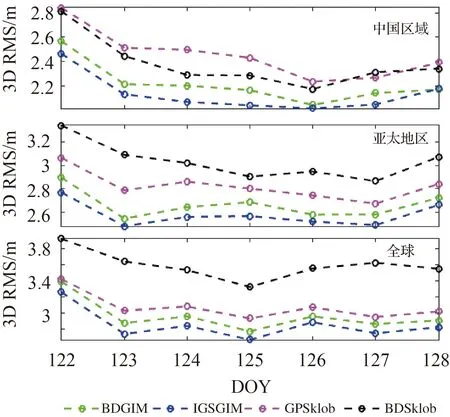
图12 2020年DOY 122—DOY 128全球各检测站三维定位精度时间序列Fig.12 BDS SPP 3D positioning accuracy time series during the period from DOY 122 to DOY 128 in 2020

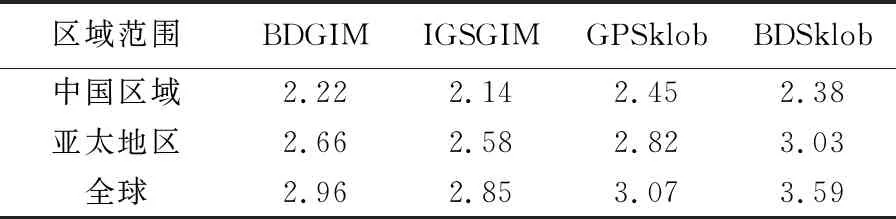
表6 2020年DOY 122—DOY 128全球各检测站三维定位精度统计

3.4 BDGIM模型发播参数与CODE发布的球谐系数对比

图13给出了2020年DOY 122—DOY 202 BDGIM模型与CODE模型播发的第一项球谐系数时间序列。可以看出，BDGIM模型与CODE播发的第一项球谐模型系数变化趋势基本一致。与CODE相比，BDGIM模型播发的第一项系数变化更为平缓，二者的差异在-1.88～1.29 TECU之间，平均偏差为-0.02 TECU，RMS为0.54 TECU。图13表明，BDGIM模型和CODE播发的球谐系数具有较强的一致性，可以较为准确地描述全球电离层TEC的整体变化形态，进一步验证了BDGIM模型播发参数计算的有效性。

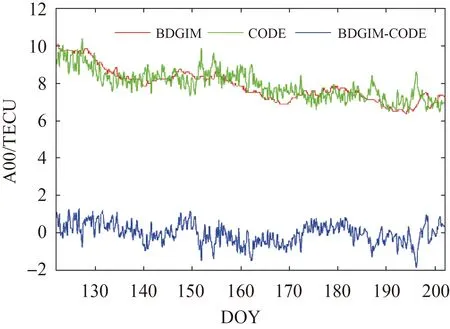
图13 2020年DOY 122—DOY 202 BDGIM与CODE播发的第1项球谐系数时间序列Fig.13 Time series of the first term spherical harmonic coefficient broadcast by BDGIM and CODE during the period from DOY 122 to DOY 202 in 2020

4 结 论

本文以IGS发布的最终GIM产品、全球83个GNSS检测站实测电离层TEC为参考，从多个精度指标及单频标准定位精度等方面，综合分析了北斗三号组网完成前后BDGIM模型在全球不同地区的应用精度，并与GPS广播的Klobuchar模型及北斗二号导航系统广播的Klobuchar模型进行对比分析研究。

分析结果表明，BDGIM模型电离层延迟改正精度在北斗三号系统组网完成前后没有显著变化。若以IGS发布的最终GIM产品为参考，BDGIM模型在中国区域、亚太地区和全球范围内，电离层修正百分比分别达到84.45%、74.74%和64.57%；若以GNSS检测站实测电离层TEC为参考，BDGIM在中国区域、亚太地区及全球各检测站的修正精度分别为73.12%、70.18%和68.06%；当BDGIM模型应用于BDS单频伪距单点定位时，在中国区域、亚太地区和全球范围内BDGIM模型可获取的三维定位精度分别为2.22、2.66和2.96 m。

随着用于计算BDGIM模型发播系数的境外北斗监测站的适度增加(目前，还没有利用中国境外北斗监测站数据计算BDGIM模型发播系数，北斗三号卫星现今播发的BDGIM参数仅由中国境内的北斗运控站数据计算得到)，BDGIM模型的电离层延迟改正精度将会得到进一步提升。后续将不断利用更多的不同时段、季节及不同区域电离层活动状态的北斗/GNSS等高精度资料，进一步深入系统分析和研究BDGIM模型的修正精度等应用性能。