不同墩高的矩形单肢薄壁空心墩动力特性的数值模拟*

沈欣茹 周正华

（南京工业大学交通运输工程学院，南京 210009）

引言

我国实施西部大开发战略已有20年，而交通工程一贯作为经济发展的生命线，更是被归为西部大开发的第一要务。西部地区地形复杂，多高山峡谷，需要修建大量的桥梁来维系线路的畅通，而在地形和通航条件以及环境等因素受到严格限制时，如果采用对称式桥梁会增加开挖量和成本，所以西部地区难以避免会出现高低墩式桥梁结构[1]。同时，西部地区地震频生，因此，研究在地震作用下的结构效应是极有必要的，其分析方法也分为理论分析、实验和数值模拟这3种。由于现实的需要，国内外已有不少学者采取不同的分析方法对高低墩的动静力特性进行了相关研究。

就静力特性，我国学者张顺民[1]用MIDAS/Civil分析连续刚构桥高低墩在不同墩差情况下的受力和变形情况，得出桥墩高度差增大时，桥梁的临界荷载会逐渐减小。董宏伟等[2]分析不同的梁高对结构整体刚度产生的影响，得出主梁梁高的增加会导致桥梁横向、竖向刚度的增大，且对于竖向刚度的影响大于横向。而朱静[3]对保持一侧墩高不变，改变另一侧墩高的跨径对称的多个连续刚构桥有限元模型进行桥墩内力及变形的计算分析，对比得出在跨径对称而墩高不对称时，桥墩高度的减小将使其抗推刚度迅速增大，从而加大墩柱弯矩。就动力特性，我国学者姜楠等[4]选取5条不同的近断层地震波运用有限元软件FRAME3D对两种不同墩高组合刚构桥进行三向地震动输入，研究其结构响应和桥墩的损伤状况，得出低墩发生损伤的部位位于墩顶、墩底、横系梁，而高墩的损伤部位主要在其下半部分。同时，程志友等[5]、周伟[6]、何伟等[7]也得出了类似的结论。此外，陈全[8]也通过三向地震动输入得出随着桥墩相对高差的增大，纵向、横向、竖向频率均增大，三向整体刚度也增大；增大桥墩的相对高差，在地震作用下，高墩墩底的弯矩、剪力会呈减少趋势，矮墩墩底情况相反。而王建忠[9]在3种不同的地震荷载工况下分别运用反应谱法和动力时程分析法对4个不同高低墩高差的桥梁结构进行地震响应分析，对比桥梁的各关键截面，得出在不同地震荷载工况下，桥梁的内力和位移存在明显差异；随着墩高差距的数倍增加，高墩弯矩的变化较矮墩要大。而耿江玮等[10]采用时程分析法研究非规则连续梁桥的非线性顺桥向地震反应，对比线性与非线性分析的结果，得出在地震作用下，线性结果将不能准确反映处于非线性状态的各墩柱的地震力；当桥墩高度相差较大时，各桥墩的变形能力差异大，矮墩会承担更大的地震力。同时，李可欣[11]运用类似方法得出线性时程分析法所得的墩顶和墩底的内力和弯矩均比非线性分析得出的结果大；桥墩高差对顺桥向刚度影响最大，而对竖向刚度影响最小。此外，周朋等[12]、倪洪将[13]也分别印证了该结论。罗松涛等[14]对5个不同桥墩高差的不对称刚构桥进行模态分析并采用反应谱法研究其空间动力特性和地震响应，得出桥墩高度的不对称性会显著影响整个桥梁结构的低阶自振周期，但对其低阶振型的影响不大，较明显的变化要到较高阶振型。李勇等[15]则结合数值分析法和振动台试验对一典型高低墩式连续梁桥进行了地震的易损性能分析。此外，还有国外学者Saiidi等[16]通过振动台试验，对不等高桥墩的多跨框架桥进行系统研究，证明了矮墩比高墩更具地震易损性。Abbasi[17]研究了从规则到高度不规则的多层框架箱梁桥的抗震性能，在桥梁的三维分析有限元模型上进行了完全非线性的时程分析，结果清楚地表明，桥梁的脆性随高度不规则度的增加而增加。

1 分析模型的建立

1.1 有限元模型的建立

建立的桥墩为单肢薄壁空心墩，截面形状为矩形，尺寸为 6 m×5 m，壁厚为 0.4 m，墩身高度为 50 m，依次调整墩高，建立5个桥墩模型：50 m、40 m、30 m、20 m和10 m，其中图1为50 m桥墩的有限元计算模型。

图 1 50 m 桥墩有限元计算模型Fig. 1 Finite element model of bridge pier

该桥墩采用C50混凝土，其材料属性：密度为2 400 kg/m3，泊松比为 0.2，弹性模量为 3.45×1010Pa；纵筋为直径32 mm的HRB335钢筋，其材料属性：密度为 7 846 kg/m3，泊松比为 0.3，弹性模量为 2×1011Pa；箍筋为直径12 mm的HPB235钢筋，其材料属性：密度为 7 851 kg/m3，泊松比为 0.3，弹性模量为 2.1×1011Pa，混凝土保护层厚度设为0.05 m。混凝土模拟为实体单元，钢筋模拟为桁架单元，将钢筋嵌入混凝土。桥墩被近似简化为墩顶自由，墩底固结的悬臂构件。

1.2 模态分析

建立桥墩的三维有限元模型后，对结构进行模态分析。表1为不同高度桥墩的前3阶自振频率计算结果（注：定义x轴为长轴方向，z轴为短轴方向）。图2为不同高度桥墩模型的前3阶自振频率对比。

对比分析不同高度桥墩模型的前3阶自振频率和振型（表1，图2—7），可以得出：对于同一阶模态，随着桥墩高度的减小，其自振频率呈现增大趋势，即桥墩结构的整体刚度在不断变大。桥墩高度从50 m降到20 m，其自振频率增加幅度较小；而高度降到20 m后，再降低桥墩高度，其自振频率增大幅度显著。从振型的性质来看，5种不同高度的桥墩模型第一阶振型均为短轴向弯曲，第二阶振型均为长轴向弯曲，前两阶振型相似，直到第三阶振型才产生差异，说明桥墩高度的变化影响的是较高阶振型。

2 地震反应数值模拟

地震荷载是工程结构主要的设计荷载之一，研究地震作用下结构的反应，对于提出合理有效的抗震措施具有重要的意义。选取大震、中震和小震3组不同的地震动分别对不同高度桥墩进行水平长轴向和短轴向输入，对比分析结构的位移和加速度反应差异。图8为3组地震动加速度时程曲线，其持续时间均为 81.9 s，时间间隔均为 0.02 s，大震峰值加速度为 3.875 m/s2，中震峰值加速度为 2.282 m/s2，小震峰值加速度为 0.639 m/s2。

表 1 模型自振特性Table 1 Natural vibration characteristics of models

图 2 模型 1 的前三阶模态振型Fig. 2 The first three modes of model 1

图 3 模型 2 的前三阶模态振型Fig. 3 The first three modes of model 2

图 4 模型 3 的前三阶模态振型Fig. 4 The first three modes of model 3

图 5 模型 4 的前三阶模态振型Fig. 5 The first three modes of model 4

图 6 模型 5 的前三阶模态振型Fig. 6 The first three modes of model 5

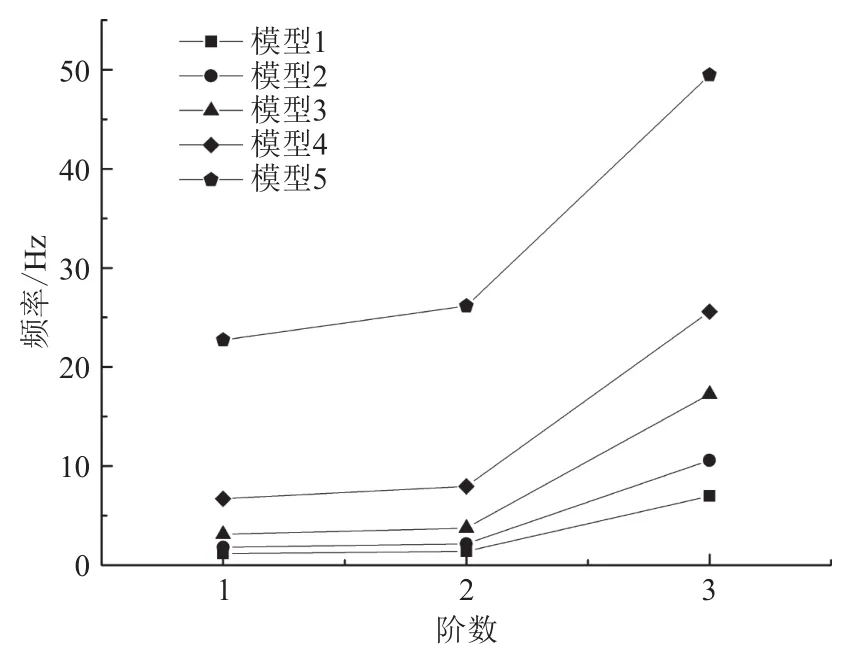
图 7 不同高度桥墩前 3 阶自振频率对比Fig. 7 Comparison of the first three natural frequencies of piers with different heights

2.1 长轴向输入

沿长轴向（即x轴向）分别输入3组地震动，不同高度桥墩墩顶各方向位移和加速度的峰值如表2—7所示。

2.1.1 位移响应分析

在大震、中震和小震作用下，不同高度桥墩沿x轴向、y轴向最大位移的变化趋势（图9）。

2.1.2 加速度响应分析

在大震、中震和小震作用下，不同高度桥墩沿x轴向、y轴向加速度峰值的变化趋势（图10）。

结合表2—7和图9—10可以得出：沿长轴向（即x轴向）输入地震动时，不同高度的桥墩都在x方向上产生最大位移响应和加速度响应。同时，沿短轴向（即z轴向）的位移和加速度最小，基本可以忽略；随着桥墩高度的增加，其刚度变大，墩顶沿x轴和y轴向的位移也不断增大；不同的地震动输入带来的结构的位移响应和加速度响应不同，在大震作用下，桥墩在各方向产生的位移和加速度响应显著大于中震和小震作用下；桥墩高度增大的同时，不同地震动输入带来的墩顶最大位移量的差异也越来越显著；桥墩高度调整到30 m时，再增加桥墩高度，在不同地震动输入下其沿x轴和y轴向的加速度峰值变化幅度基本趋于平缓；桥墩高度为10 m时，在地震作用下结构的位移响应很小，基本可以忽略不计。

图 8 大、中、小震加速度时程曲线Fig. 8 Acceleration time histories of large，medium and small earthquakes

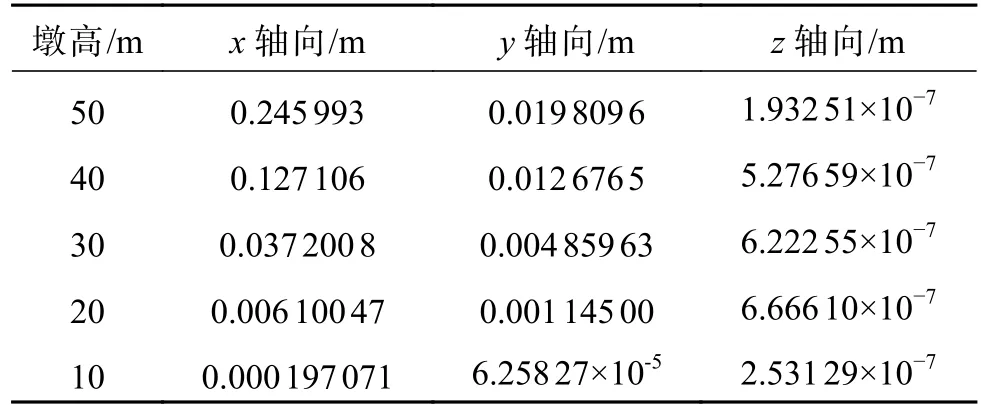
表 2 大震作用下各方向最大位移Table 2 Maximum displacements in all directions under large earthquake

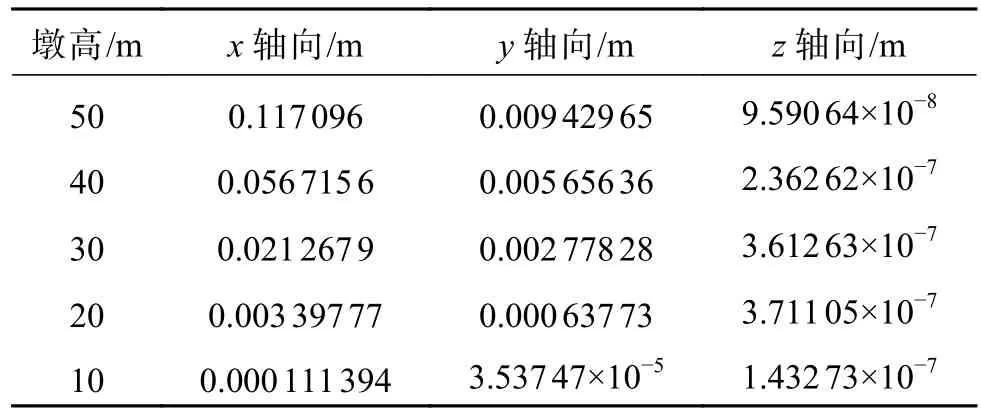
表 3 中震作用下各方向最大位移Table 3 Maximum displacements in all directions under medium earthquake

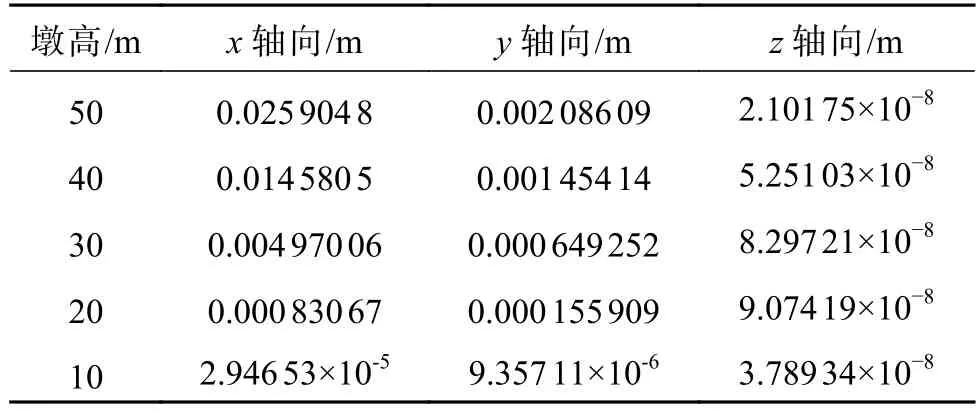
表 4 小震作用下各方向最大位移Table 4 Maximum displacements in all directions under small earthquakes

表 5 大震作用下各方向加速度峰值Table 5 Peak accelerations in all directions under large earthquake

2.2 短轴向输入

沿短轴向（即z轴向）分别输入3组地震动，不同高度桥墩墩顶各方向位移和加速度的峰值如表8—13所示。

2.2.1 位移响应分析

在大震、中震和小震作用下，不同高度桥墩沿y轴向、z轴向最大位移的变化趋势（图11）。

表 6 中震作用下各方向加速度峰值Table 6 Peak accelerations in all directions under medium earthquake

表 7 小震作用下各方向加速度峰值Table 7 Peak accelerations in all directions under small earthquake

图 9 不同高度桥墩沿各轴向最大位移Fig. 9 Maximum displacement of piers with different heights along each axis

图 10 不同高度桥墩沿各轴向加速度峰值Fig. 10 Peak acceleration of piers with different heights along each axis

2.2.2 加速度响应分析

在大震、中震和小震作用下，不同高度桥墩沿y轴向、z轴向加速度峰值的变化趋势（图12）。

结合表8—13和图11—12可以得出：沿短轴向（即z轴向）输入地震动时，不同高度的桥墩都在z方向上产生最大位移响应和加速度响应，同时，沿长轴向（即x轴向）的位移和加速度最小，基本可以忽略；随着桥墩高度的增加，其刚度变大，墩顶沿y轴和z轴向的位移也不断增大；不同的地震动输入带来的结构的位移响应和加速度响应不同，在大震作用下，桥墩在各方向产生的位移和加速度响应显著大于中震和小震作用下；桥墩高度增大的同时，不同地震动输入带来的墩顶最大位移量的差异也越来越显著；桥墩高度调整到30 m时，再增加桥墩高度，在不同地震动输入下其沿y轴和z轴向的加速度峰值变化幅度均趋于平缓；桥墩高度为10 m时，在地震作用下结构的位移响应很小，基本可以忽略不计。

表 8 大震作用下各方向最大位移Table 8 Maximum displacements in all directions under large earthquake

表 9 中震作用下各方向最大位移Table 9 Maximum displacements in all directions under medium earthquake

表 10 小震作用下各方向最大位移Table 10 Maximum displacements in all directions under small earthquake

表 11 大震作用下各方向加速度峰值Table 11 Peak accelerations in all directions under large earthquake

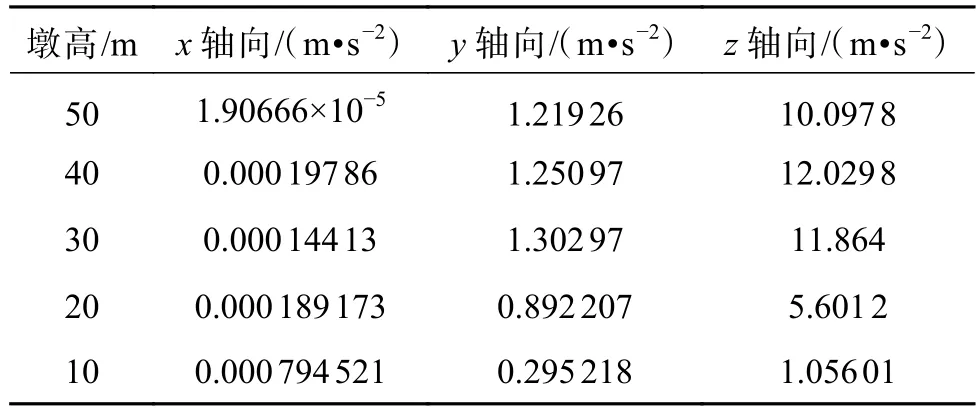
表 12 中震作用下各方向加速度峰值Table 12 Peak accelerations in all directions under medium earthquake

表 13 小震作用下各方向加速度峰值Table 13 Peak accelerations in all directions under small earthquake

图 11 不同高度桥墩沿各轴向最大位移Fig. 11 Maximum displacement of piers with different heights along each axis

图 12 不同高度桥墩沿各轴向加速度峰值Fig. 12 Peak acceleration of piers with different heights along each axis

3 结论

为研究高低墩的动力特性，借助ABAQUS建立5种不同高度桥墩的有限元模型，分别对其进行模态分析，并沿长轴向和短轴向两个方向分别输入3组不同的地震动，研究其地震响应差异。通过大量的数据分析，得出以下结论：

（1）对于同一阶模态，随着桥墩高度的减小，结构的整体刚度不断变大，其自振频率呈增大趋势；同时，桥墩高度的变化影响的是较高阶振型。

（2）沿长轴向输入地震动时，桥墩墩顶会在长轴向产生最大位移响应和加速度响应，在短轴向的位移和加速度响应很小，基本可以忽略；而沿短轴向输入地震动时，桥墩墩顶会在短轴向产生最大位移响应和加速度响应，在长轴向的位移和加速度响应很小，基本可以忽略。

（3）在不同的地震动输入下，结构的位移响应和加速度响应差异十分显著，在大震作用下，桥墩在各个方向上产生的位移和加速度响应都要显著大于在中震和小震作用下。

（4）桥墩高度的减小可以显著减小结构的位移和加速度响应，当桥墩高度调整到10 m时，受地震作用影响很小，几乎不产生位移变形。