Resonance Y-type soliton solutions and some new types of hybrid solutions in the(2+1)-dimensional Sawada–Kotera equation

Jiaheng Li,Qingqing Chen and Biao Li

School of Mathematics and Statistics,Ningbo University,Ningbo 315211,China

Abstract In this paper,based on N-soliton solutions,we introduce a new constraint among parameters to find the resonance Y-type soliton solutions in (2+1)-dimensional integrable systems.Then,we take the(2+1)-dimensional Sawada–Kotera equation as an example to illustrate how to generate these resonance Y-type soliton solutions with this new constraint.Next,by the long wave limit method,velocity resonance and module resonance,we can obtain some new types of hybrid solutions of resonance Y-type solitons with line waves,breather waves,high-order lump waves respectively.Finally,we also study the dynamics of these interaction solutions and indicate mathematically that these interactions are elastic.

Keywords: resonance Y-type solitons,(2+1)-dimensional Sawada–Kotera equation,hybrid solutions

1.Introduction

In the field of integrable systems,through various constraints on the N-soliton solutions from Hirota bilinear method,we can get different types of soliton in the bound state.By introducing module resonant [1–3],N-soliton solutions convert into breather waves that change periodically over time.Taking Hirota bilinear method and the long wave limit method,some exact solutions can be obtained,such as lump waves and line waves[4,5].The research progress of soliton molecule experiment promotes the theory development of velocity resonance mechanism [6–8].

Meanwhile,the solutions of resonance Y-type soliton continue to be studied by many scholars.Such as the resonance soliton is observed due to a photoinduced gap in wave number [9].In most studies of resonance Y-type soliton,the authors set the solution [10–12] as the following form

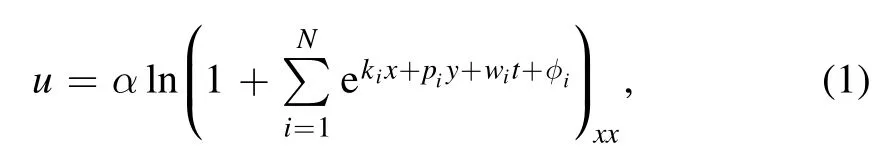
however,because of the peculiarity of the form,it’s too hard to get the hybrid solutions between resonance Y-type soliton and other types of solitons.Recently,Chen et al put forward a new form of N-soliton solutions [11] as follow

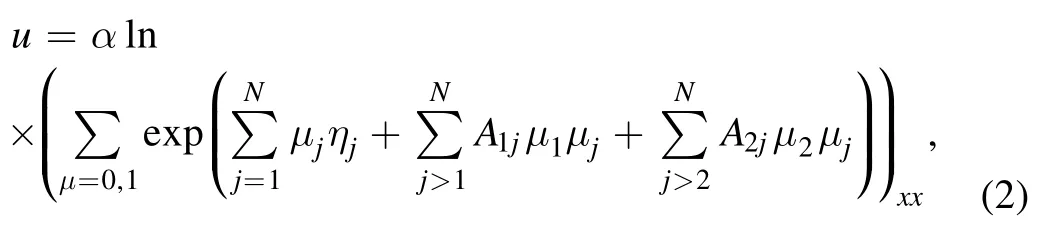
where ηj,Aijrefer to [11].We can get some hybrid solutions by this method,like an interactional solution between a firstorder lump wave and N-resonance Y-type solitons.But on the basis of equation(2),no matter what constraints you make,as a result of equation (2) has fewer terms than the classic Nsoliton solutions,we cannot obtain some interaction solution of resonance Y-type solitons with resonance Y-type solitons,breather waves,line waves,high-order lump waves respectively.

Based on classic N-soliton solutions,by the new constraint in this paper,we can obtain some new types of hybrid solutions of resonance Y-type solitons with resonance Y-type solitons,breather waves,line waves,and high-order lump waves respectively.Without generality,we take the(2+1)-dimensional Sawada–Kotera (SK) equation as an example

where u(x,y,t) is a function of the variables x,y and t,and equation (3) was first proposed by Konopelchenko and Dubrovsky [13].In the past few decades,many scholars have paid more attention to the study of equation(3).For instance,the algebraic-geometric explicit solution can be obtained in [14],symmetry analysis was studied in [15–18].Lots of different solutions including multi-soliton solutions,double periodic wave solutions,lump wave solutions,and interaction solutions have been obtained for equation (3) in [19–24].

In this paper,we mainly obtain the resonance Y-type soliton solutions and some new types of hybrid solutions of equation (3) with the new constraint.The rest of the paper is arranged as follows.In section 2,we obtain exact solutions including resonance Y-type soliton and resonance Y-type soliton with the new constraint.In section 21,some new types of hybrid solutions of equation (3) can be obtained by taking suitable parameter constraints and the long wave limit method.Finally,our conclusion is presented in section 4.

2.Resonance Y-type soliton solutions of the(2+1)-dimensional SK equation

Using Hirota bilinear method,N-soliton solution to equation (3) can be easily found

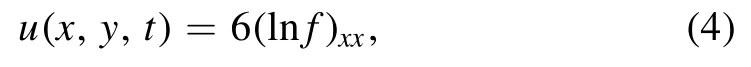
where

with

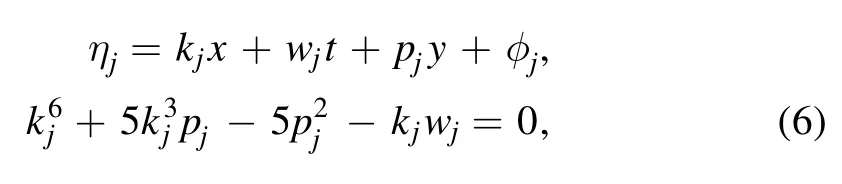
and

Supplement

In this paper,we introduce a new supplement to theexp(x) :exp (x)=0 is true if and only ifx= ln (0) .As a result of the regulation,exp (x+ln (0))= 0 exp (x)=0.The aim of this supplementary definition is to systematically get rid of the partial terms in equation (5).If allAjs= ln (0) ,then equation(5)is equivalent to equation(1).Moreover,if partialAjs=ln (0) ,3 ≤j ＜s ≤N,then equation (5) will degenerate into equation (2).According to this supplement,some very interesting conclusions will appear as follows.

Proposition 1Based on the N-soliton solutions,the interaction solutions of M-resonance Y-type solitons and L-resonance Y-type solitons can be derived via the following constraints

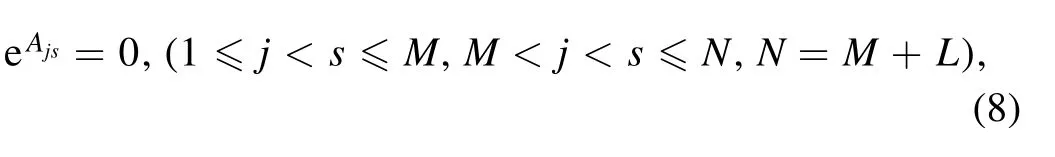
with

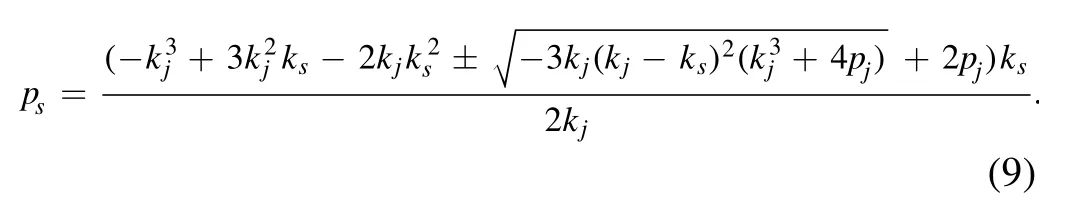
Using equations (3)–(8),we can obtain equation (9)clearly.Where the M-resonance Y-type solitons in proposition 1 generated by M-line waves.Paying attention to the equation (9),in fact,has two cases: they have two types of different openings.At the same time,these cases can be illustrated by brief example as follows.

Based on the N-soliton solutions,if N=2,we can obtain two different solitons,just like two different types of openings of 2-resonance Y-type soliton as showing in figure 1.

In fact,as shown in figure 1.It is not difficult to find that the values of figures 1(a) and (b) are only different in p2,so we illustrate two cases of equation (9).

Furthermore,if N=3,we find the change of resonance Y-type soliton with time going by.

As shown in figures 1 and 2,many scholars call them fussionable waves or fissionable waves [10–12],but we can see clearly,with time going by,these resonance solitons are only ceaselessly translating instead of fusion or fission.So,it’s more reasonable to call them resonance Y-type solitons.

In addition,if proposition 1 with M=2,L=2,the expression described an interaction between two 2-resonance Y-type soliton has the following form

with

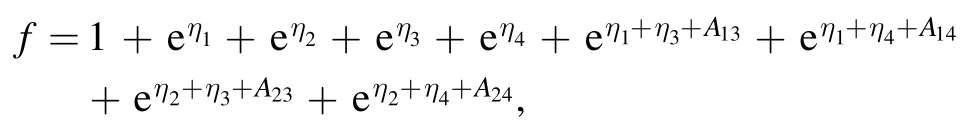
where the relevant parameters ηj,Ajshave been given in equations (7) and (8).

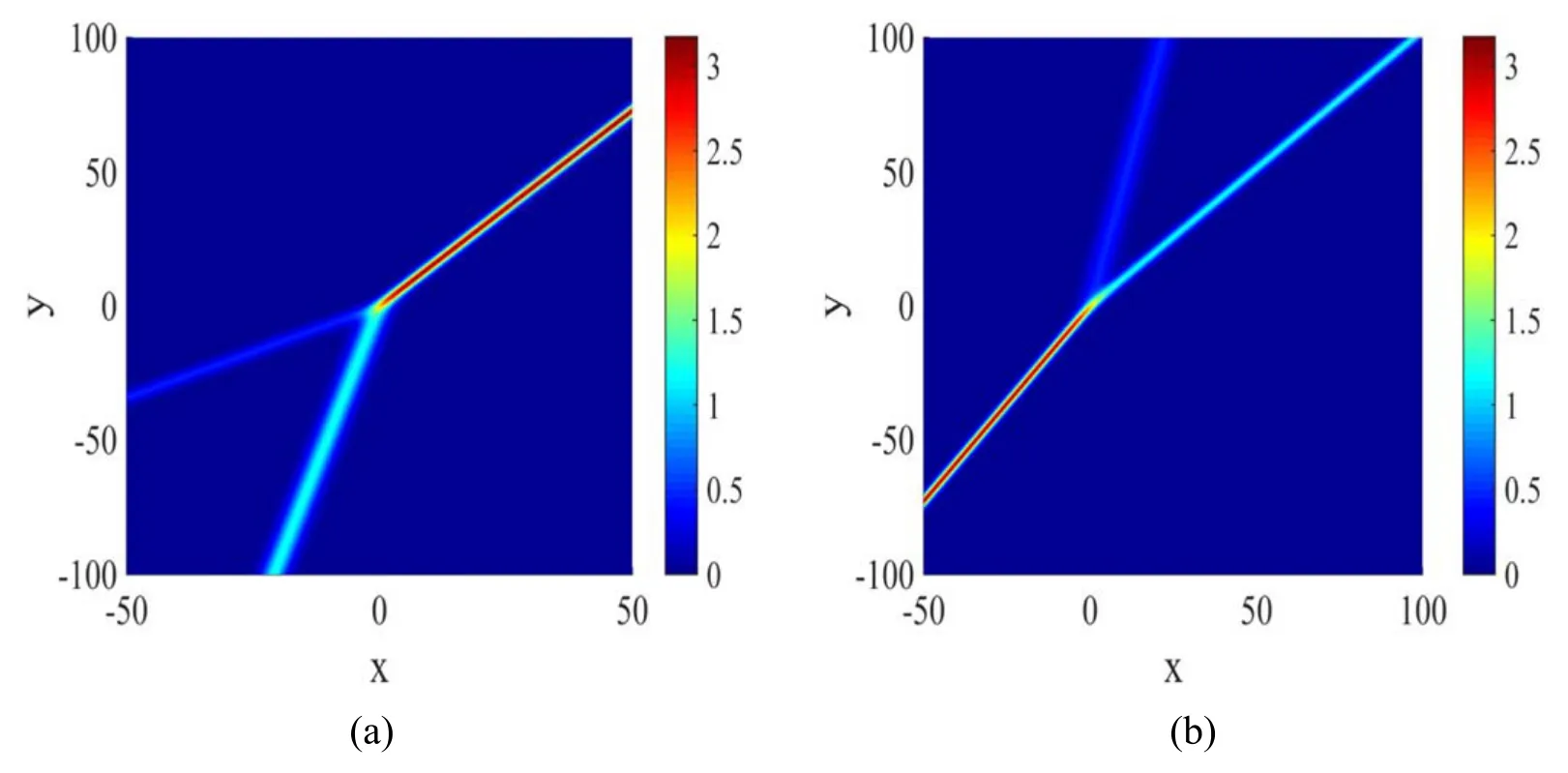
Figure 1.Density plot of 2-resonance Y-type solitons at t=0,with ,p1= − 1 ,φ1= 0,φ2=0,and: (a)

Figure 2.Density plot of 3-resonance Y-type solitons withφ1=0,φ2=0,φ3=0.

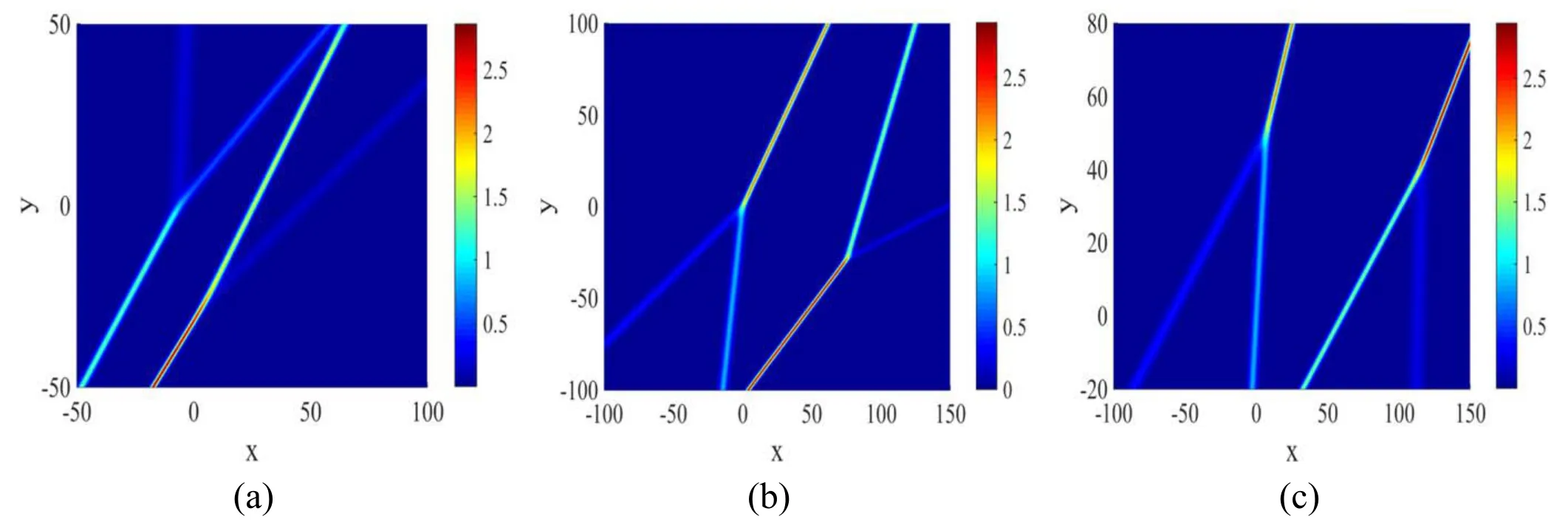
Figure 3.Three different types of interactions of two 2-resonance Y-type solitons at t=0,described by equation (10) with: (a)k1= φ1=30,φ2=−20,φ3=0,φ4=0; (b)k1=φ1=−140,φ2=−80,φ3=0,φ4=0; (c)k1=φ1=−100,φ2=−60,φ3=−30,φ4=0.

Taking the appropriate parameters,equation (10) can describe the three basic types of interaction between two 2-resonance Y-type solitons.The three pictures in figure 3 vividly illustrate these types of interactions.The interactions between line waves are elastic,so it is reasonable to believe that the interactions as shown in figure 3,reduced from the Nsoliton solutions,are also elastic.As is known to all,there is a mature method to obtain pure resonance Y-type solitons[10–12],but the interaction represented by proposition 1 has not been discovered.

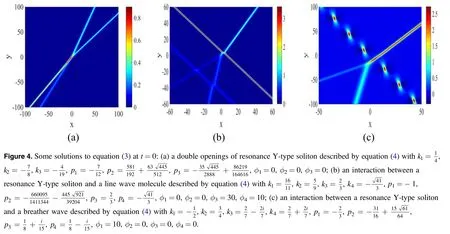
Proposition 1 contains a special case:L=0.In this case,the N-soliton solution can only be reduced to a N-resonance Y-type soliton,and most studies only obtain pure resonance Y-type solitons.In fact,by selecting appropriate parameters,double openings of resonance Y-type soliton shown in figure 4(a).In addition,if the constraints proposed in this paper are combined with velocity resonance and module resonance,some hybrid solutions including but not limited to resonance Y-type solitons can be derived from equation (4).For example,if equation (4) satisfies these constraints proposed in this paper and partial velocity resonance

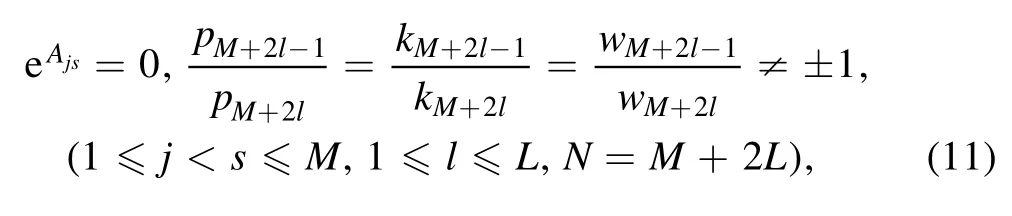
we can derive a hybrid solution of a M-resonance Y-type soliton and a L-line wave molecule.When equation (4)satisfies

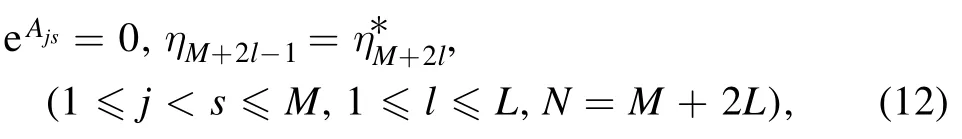
an interactional solution between a M-resonance Y-type soliton and a L-order breather wave can be obtained.

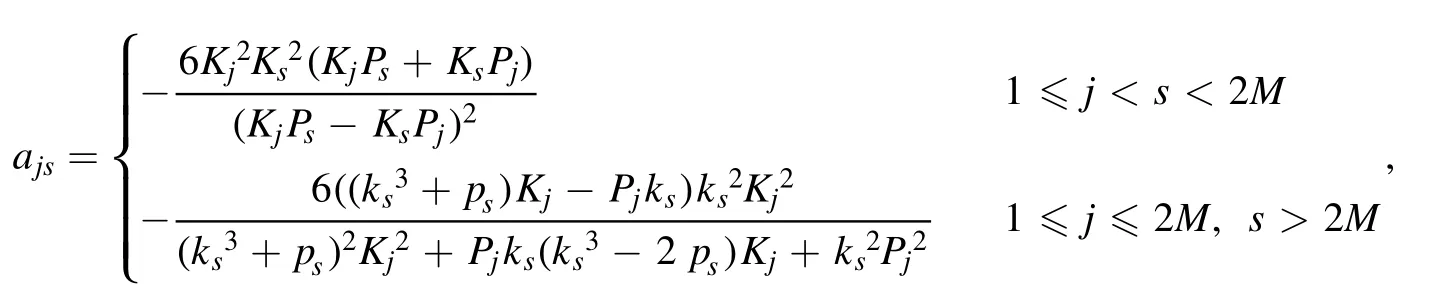
3.Interactions of resonance Y-type solitons and high-order lump waves in the (2+1)-dimensional SK equation

Based on the constraint condition equation (9),which is mentioned in this paper and the long wave limit method,a direct method is presented for obtaining the interactions between high-order lump waves and resonance Y-type solitons.Referring to some interesting work [7,25],we can directly draw the following conclusions.

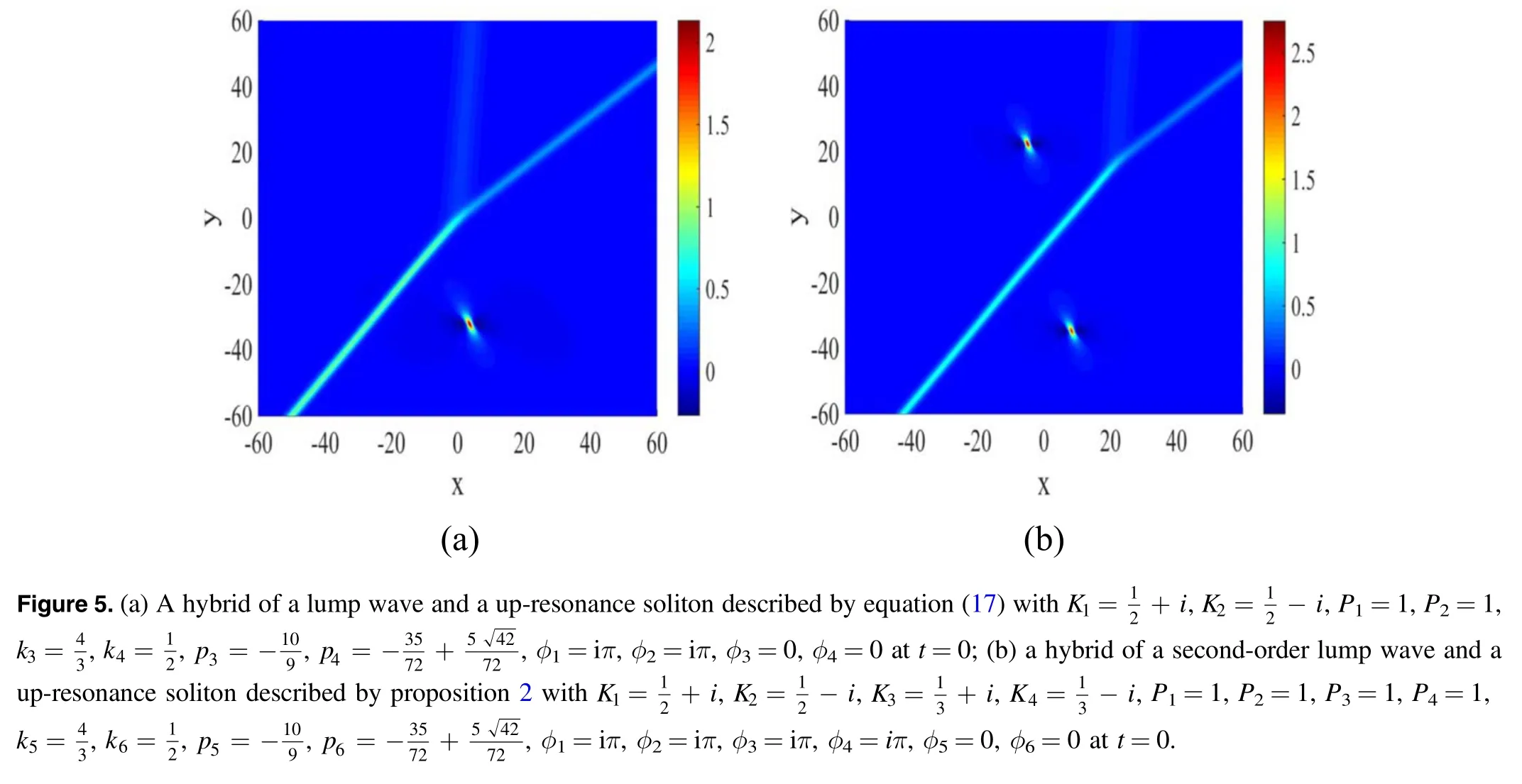
Proposition 2An interactional solution between a M-order lump wave and a L-resonance Y-type soliton can be derived if the following constraints are applied to the N-soliton solution

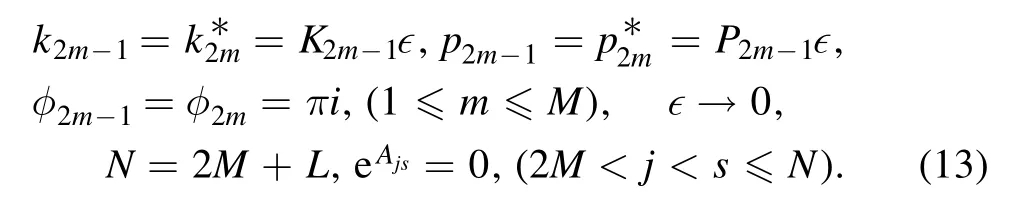
And the trajectories of the lump wave limited by the parameters {K2m−1,P2m−1,K2m,P2m} before and after the interaction of the L-resonance Y-type solitons are

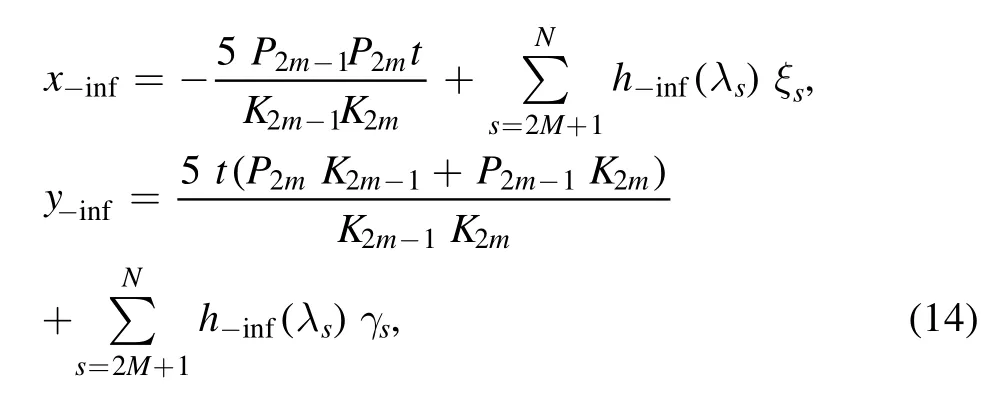
with

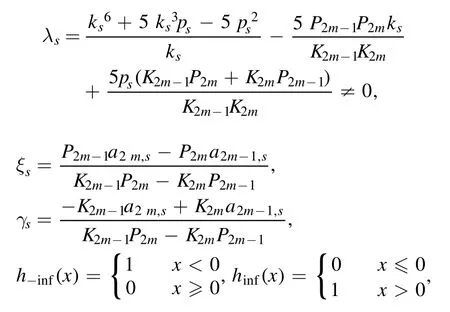
and

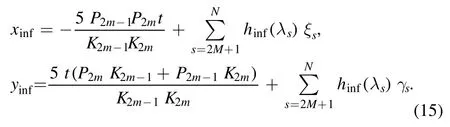
Moreover,the wave height h of the lump wave does not change before and after the interaction,as the following form

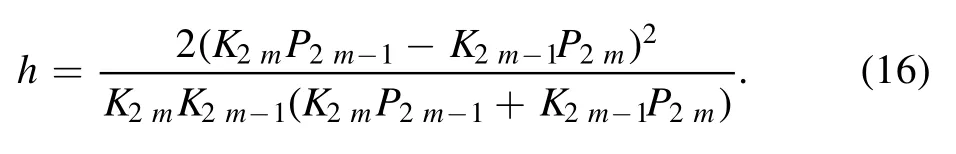
Based on Hirota bilinear method and the long wave limit method,on the one hand,we introduce a new constraint to systematically get rid of some terms of the N-soliton solutions to get proposition 2.

In [11],the authors remove so many terms that only obtain a hybrid solution between a first-order lump wave and a L-resonance Y-type soliton,if we want to obtain more generalized interactions between high-order lump waves and a L-resonance Y-type soliton,more terms must be reserved.On the other hand,we study the dynamics of these interactions described by proposition 2 and mathematically indicate that these interactions are elastic.

Particularly,if M=1,L=2 in proposition 2,we can find the expression for a hybrid solution of a first-order lump wave and a 2-resonance Y-type soliton as follows

with

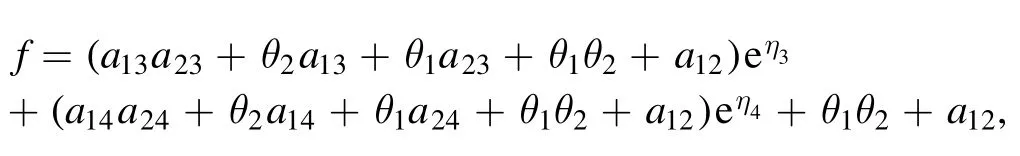
4.Conclusion

Based on N-soliton solutions generated by Hirota bilinear method,we introduce a new constraint among parameters to find the resonance Y-type soliton solutions in (2+1)-dimensional integrable systems.In this paper,we take the(2+1)-dimensional SK equation as an example to introduce how to generate these interesting phenomena in detail.At first,we give the resonance Y-type soliton solutions in figures 1 and 2.second,on the one hand,by getting rid of some terms of the classic N-soliton solutions to obtain abundant resonance Y-type soliton solutions with the new constraint condition given by proposition 1,and figure 3 intuitively shows the three fundamental interactions;on the other hand,by means of velocity resonance,module resonance and the long wave limits method,some new types of hybrid solutions of resonance Y-type solitons with line waves,breather waves,and high-order lump waves respectively are obtained shown in figures 4 and 5.In the meantime,we study in depth the dynamic properties of the interactions described in proposition 2,and clearly show that the interactions are elastic.As for whether other(2+1)-dimensional integrable equations can also obtain resonant Y-type solitons,and whether there are some limitations,it is worth looking forward to study.In order to obtain better results,we will do further research in the following time.Finally,we hope that the method for the resonance Y-type soliton solutions and these new types of hybrid solutions obtained in the paper can provide some help in the field of nonlinear science and physics.

Acknowledgment

This work is supported by National Natural Science Foundation of China under Grant Nos.11775121 and 11435005,and K C Wong Magna Fund in Ningbo University.