Pure annihilation decays of and in the PQCD approach

Yutong Chen (陈禹同),Zewen Jiang (蒋泽文) and Xin Liu (刘新)

Department of Physics,Jiangsu Normal University,Xuzhou 221116,China

Abstract We study the CP-averaged branching fractions and the CP-violating asymmetries in the pure annihilation decays of and wheredenotes the scalar a0(980) and a0(1450) and with the perturbative QCD factorization approach under the assumption of two-quark structure for the a0 and states.The numerical results show that the branching ratios of thedecays are in the order of 10−6,while the decay rates of the modes are in the order of 10−5.In light of the measured modes with the same quark components in the pseudoscalar sector,namely,→ K+ K −andthe predictions for the considered decay modes in this work are expected to be measured at the Large Hadron Collider beauty and/or Belle-II experiments in the (near) future.Meanwhile,it is of great interest to find that the twist-3 distribution amplitudes φS and φT with inclusion of the Gegenbauer polynomials for the scalar a0(1450)and states in scenario 2 contribute slightly to the branching ratios while significantly to the CP violations in theand →a0 (1 450)+ a0 (1 450)−decays,which indicates that,compared to the asymptotic φS and φT,these Gegenbauer polynomials could change the strong phases evidently in these pure annihilation decay channels.These predictions await for the future confirmation experimentally,which could further provide useful information to help explore the inner structure of the scalars and shed light on the annihilation decay mechanism.

Keywords: B meson decays,perturbative QCD factorization approach,light scalar mesons,branching ratios,CP-violating asymmetries

In the heavy flavor B physics,the annihilation diagrams are highly important in understanding the (non-)perturbative dynamics involved in the related decays,although which are generally considered as the power suppressed ones and then ever neglected because of not knowing how to effectively calculate them at the early stage of investigating the B meson decays [1–3]1It is worth stressing that the annihilation diagrams seem much more important in understanding the dynamics contained in the charmed meson decays,e.g.see [4–7] for detail..However,to interpret well the fundamental quantity,namely,the CP-violating asymmetry,one realized that the annihilation diagrams should be included essentially.Although,to date,both of the soft-collinear effective theory[8] and the pertubative QCD factorization (PQCD) approach[9–11] believed that the annihilation diagrams could be perturbatively calculated,the extremely different observations still made this issue controversial,namely,an almost real amplitude with a tiny strong phase was obtained in the former framework by introducing the zero-bin subtraction [12]; and in contrast,an almost imaginary one with a large strong phase appeared in the latter formalism naturally by keeping the transverse momentum kTof valence quark[13].Furthermore,it is stressed that more recent works based on the QCD factorization approach [3,14],one of the popular factorization methods in the current market,claimed that a complex contribution arising from the annihilation diagrams with significant imaginary parts should be essential in the B(s)→PP,PV and VV decays by fitting to experimental data [15–23].Phenomenologically speaking,they supported the viewpoint of the PQCD approach on the effective calculations of the annihilation diagrams to some extent.And what is more,the measurements from the Large Hadron Collider beauty(LHCb) experiment on the pure annihilation modes [24–26],i.e.andconfirmed the predictions of their branching ratios in the PQCD approach at leading order [27,28].Undoubtedly,the good agreement between theory and experiment is very exciting and inspiring.Therefore,in order to provide solid foundation to understand the annihilation decay mechanism,more and more investigations on the annihilation diagrams in the PQCD approach are necessary.

Motivated by this success,we shall study theanddecays within the PQCD approach at leading order in this work,where a0anddenote the light scalar states a0(980) and a0(1450),and(800) (o rκ)and(1 430),respectively.Before proceeding,it is essential to give a short review on the current status about the light scalar states a0and.It is well known that the description on the inner structure of light scalars is still in controversial (for a review,see e.g.[29–31]).The states a0(980) and κ with masses below or close to 1 GeV are classified into one nonet,while those ones a0(1450) and1 430)with masses above 1 GeV belong to the other nonet.It has been stressed that these two nonets are hard to be considered as the low-lyingstates simultaneously due to the major difficulties,e.g.see [32] for detail.Therefore,two typical scenarios are suggested for the classification of these light scalar states [33]: in scenario 1(S1),a0(980) and κ are the lowest-lyingstates,while a0(1450) and(1 430)are the first excitedstates correspondingly; in scenario 2(S2),a0(980) and κ are treated as four-quark states,and then a0(1450) and(1 430)are considered as the lowest-lying two-quark states.In the present work,we shall consider the decays ofandwith the scalars in the two-quark model.Then,it is easily found that the considered decays have the same quark components as those measured ones,i.e.andin the pseudoscalar sector.Therefore,the LHCb and/or Belle-II experiments could potentially make a sound examination on the predictions about the branching ratios and/or the CP violations of the consideredanddecays in the PQCD approach.

At the quark level,the consideredanddecays are induced by theand thetransitions,respectively.The related weak effective Hamiltonian Heffcan be written as [34],

with the Fermi constant GF=1.166 39×10−5GeV−2,the Cabibbo–Kobayashi–Maskawa(CKM)matrix elements Vu(t)band Vu(t)Q,the light Q=d,s quark,and the Wilson coefficients Ci(μ) at the renormalization scale μ.The local fourquark operators Oi(i=1,…,10) are written as

• Tree operators

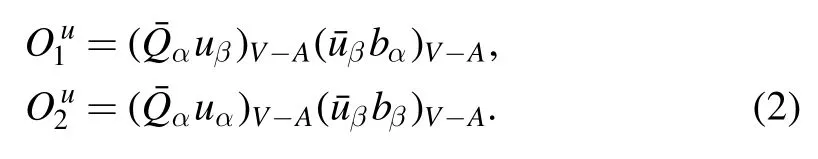
• QCD penguin operators

• Electroweak penguin operators

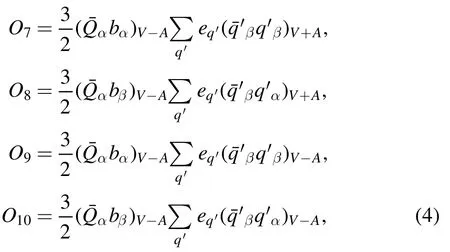
with the color indices α,β and the notationsThe indexq′in the summation of the above operators runs through u,d,s,c,and b.Note that we will use the leading order Wilson coefficients since we work in the framework of the PQCD approach at leading order.For the renormalization group evolution of the Wilson coefficients from higher scale to lower scale,we will adopt straightforwardly the formulas as given in [9,10].

The Feynman diagrams of thedecays at leading order in the PQCD formalism are illustrated in figure 1: figures 1(a) and (b) describe the factorizable annihilation(fa)diagrams,while figures 1(c)and(d)describe the nonfactorizable annihilation (nfa) ones.By replacing the s and d quarks in thedecays with the d and s ones correspondingly,then we can obtain the annihilation modesdirectly.As we know,several B →SS decays with S denoting the scalar mesons have been studied in the PQCD approach [35–39].Therefore,the analytic expressions for the decay amplitudes of the consideredanddecays can be found easily,for example,in the[37–39].Thedecay amplitudes have been presented in the PQCD approach [39].Then,we just need to replace theandstates in[39]with theand a0ones,as well as the related CKM matrix elements,to obtain easily the corresponding information of thedecays in the PQCD approach.Hence,for simplicity,we will not collect the aforementioned formulas in this paper.The interested readers can refer to [39] for detail.

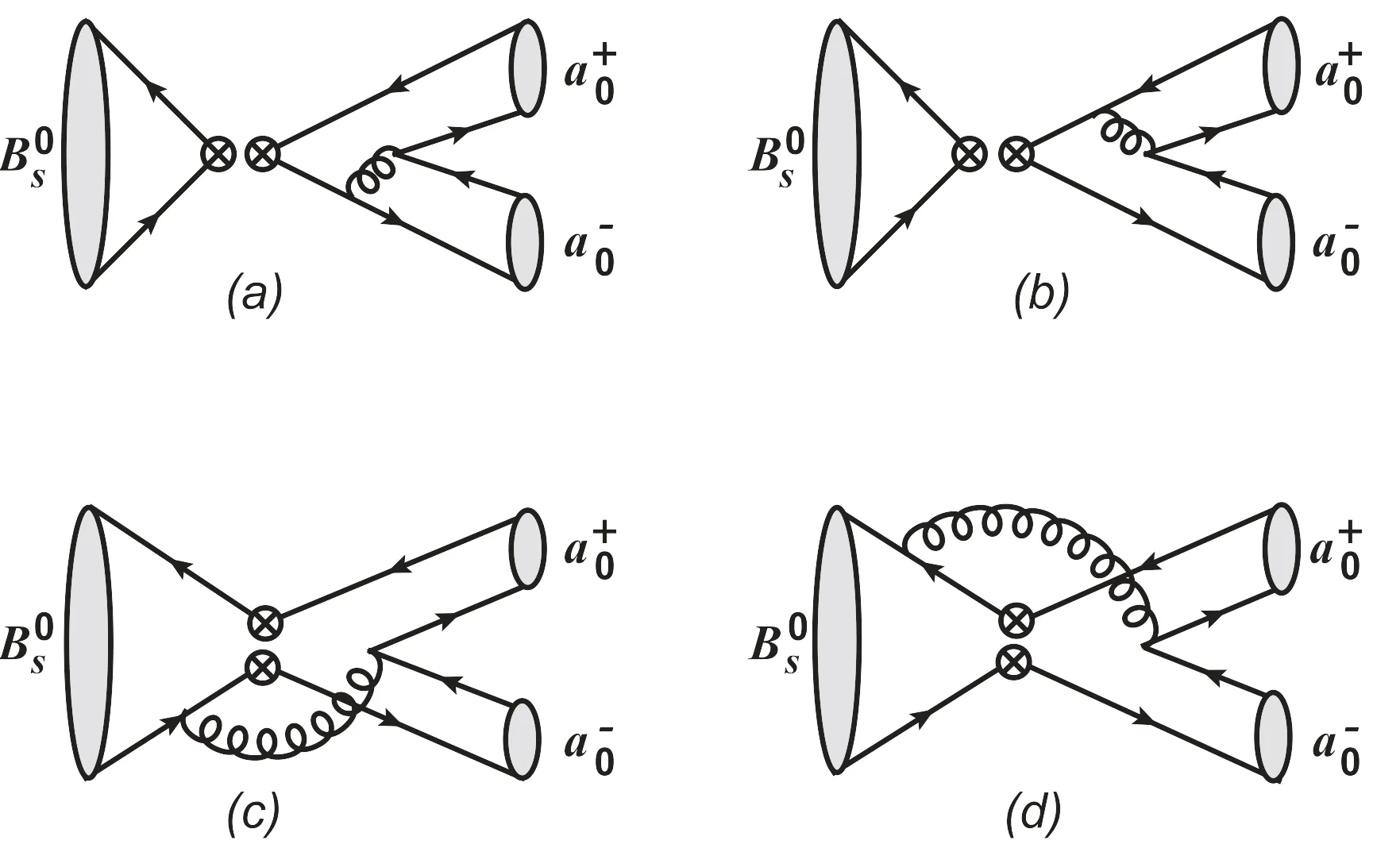
Figure 1.Leading order Feynman diagrams for decays in the PQCD formalism.

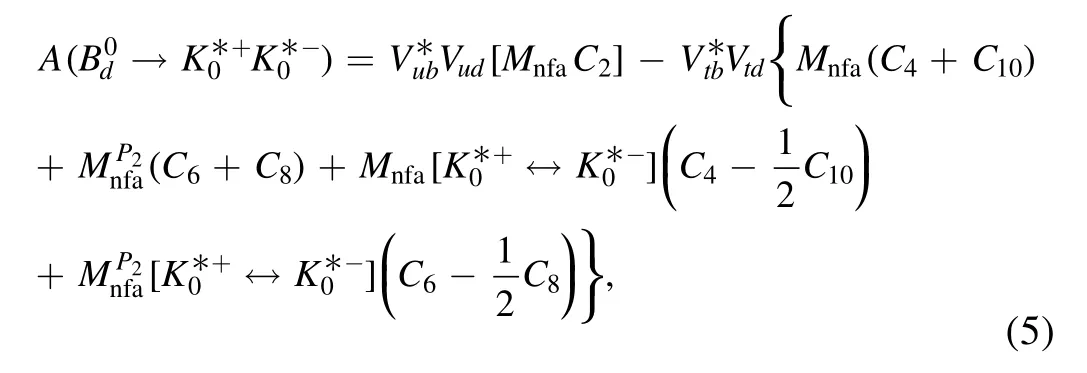
where Mnfaandstand for the nonfactorizable annihilation amplitudes arising from the (V −A)(V −A) and (S −P)(S+P) currents [39],respectively.Moreover,the almost exact cancellation of the factorizable annihilation amplitudes appear in the considered two decay modes due to the very small flavor symmetry breaking effects,which can be seen in the numerical calculations later.Similarly,we can easily obtain thedecay amplitude by the corresponding replacement of d ↔s in theone,that is,

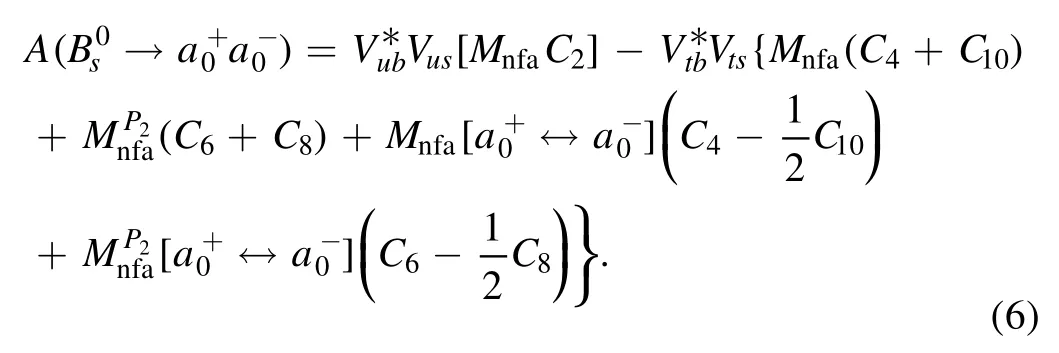
Then,we can turn to the numerical calculations of the CP-averaged branching ratios and the CP-violating asymmetries of theanddecays in the PQCD approach.Some comments on the nonperturbative inputs are listed essentially as follows:

(a) For the heavyandmesons,the wave functions and the distribution amplitudes,and the decay constants are same as those utilized in [39],but with the updated lifetimes= 1.52ps and= 1.509ps [40].It is worth mentioning that,due to its highly small effects,namely,the power-suppressed 1/mBcontributions to B decays in final states with energetic light particles[10,41],the high twist contributions from the B meson wave function in the considered pure annihilation channels have to be left for future studies associated with the precise measurements.For recent development about the B meson wave function and/or distribution amplitude,please see references,e.g.[41–46]for detail.

(b) For the considered light scalar a0andstates,the decay constants and the Gegenbauer moments in the distribution amplitudes2It is necessary to mention that we firstly adopt the asymptotic form of the twist-3 distribution amplitudes φS and φT(T3A)in the numerical calculations here as usual [33,47].And then we will estimate the effects in this work arising from the twist-3 distribution amplitudes with inclusion of the Gegenbauer polynomials(T3G)in S2 later.It is noted that only the T3G form in S2 is available currently [48].have been derived at the normalization scale μ=1 GeV in the QCD sum rule method [33]:

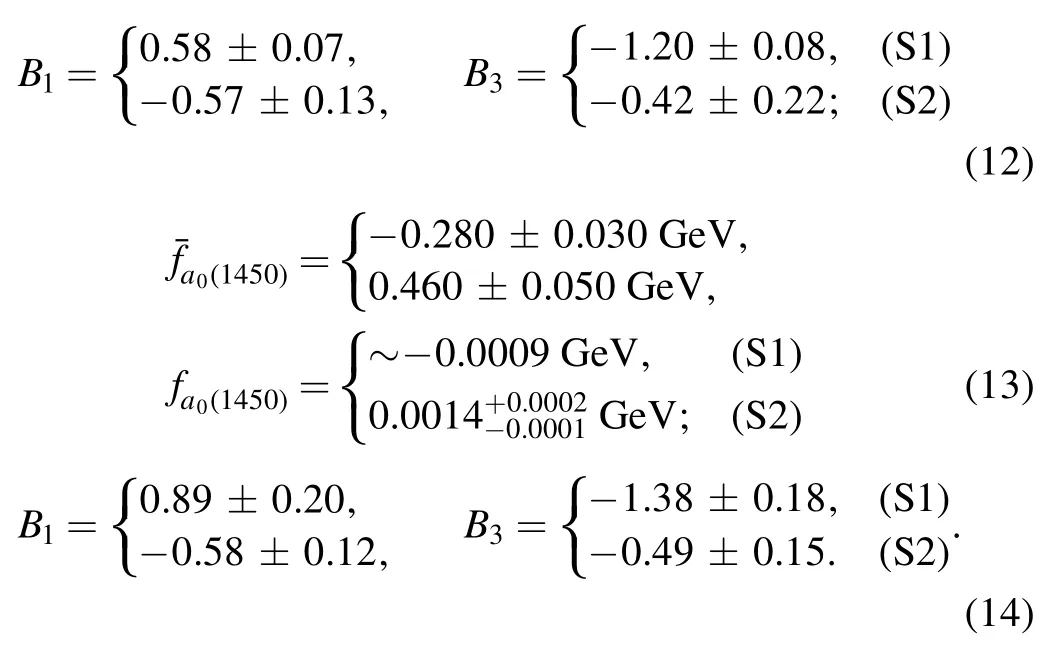
Note that the scale-dependent scalar decay constantand the vector decay constant fSare related with each other through the following relation [33],

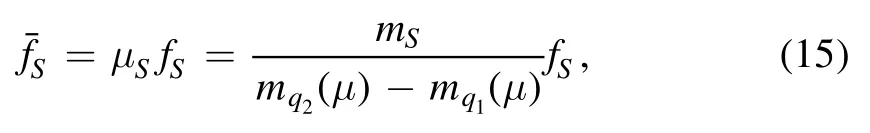
in which mSis the mass of the scalar meson,andmq2andmq1are the running quark masses.It is worth pointing out that for the a0states,the isospin symmetry breaking effects from the u and d quark masses are considered.Therefore,the running quark masses for the strange quark and the nonstrange light quarks can be read as ms=0.128 GeV,md=0.006 GeV, and mu=0.003 GeV, respectively,which are translated from those at the MS scale μ ≈2 GeV [40]. For the masses of the a0andstates,the values mκ=0.824 GeV,ma0(980)=0.980 GeV,=1.425 GeV,and=1.474GeV will be adopted in the numerical calculations3As inferred from the Review of Particle Physics[24],the considered scalar a0 andstates are also with finite widths. Generally speaking, the width effect could change the numerical results with different extent [49, 50]. In principle, we should consider the width effect to make relevant predictions more precise. However, it is unfortunate that the distribution amplitudes for the considered S-wave resonance states with the constrained parameters,e.g.Gegenbauer moments,are currently unavailable.Therefore,we have to leave the width effect in this work for future investigations elsewhere. As inferred from the Review of Particle Physics[24],the considered scalar a0 andstates are also with finite widths.Generally speaking,the width effect could change the numerical results with different extent [49,50].In principle,we should consider the width effect to make relevant predictions more precise.However,it is unfortunate that the distribution amplitudes for the considered S-wave resonance states with the constrained parameters,e.g.Gegenbauer moments,are currently unavailable.Therefore,we have to leave the width effect in this work for future investigations elsewhere..

(c) For the CKM matrix elements, we also adopt the Wolfenstein parametrization at leading order, but with the updated parameters A=0.836, λ=0.22453,[40].

Now, we present the numerical results of theanddecays in the PQCD formalism.Firstly,the PQCD predictions of the CP-averaged branching ratios can be read as follows:

and

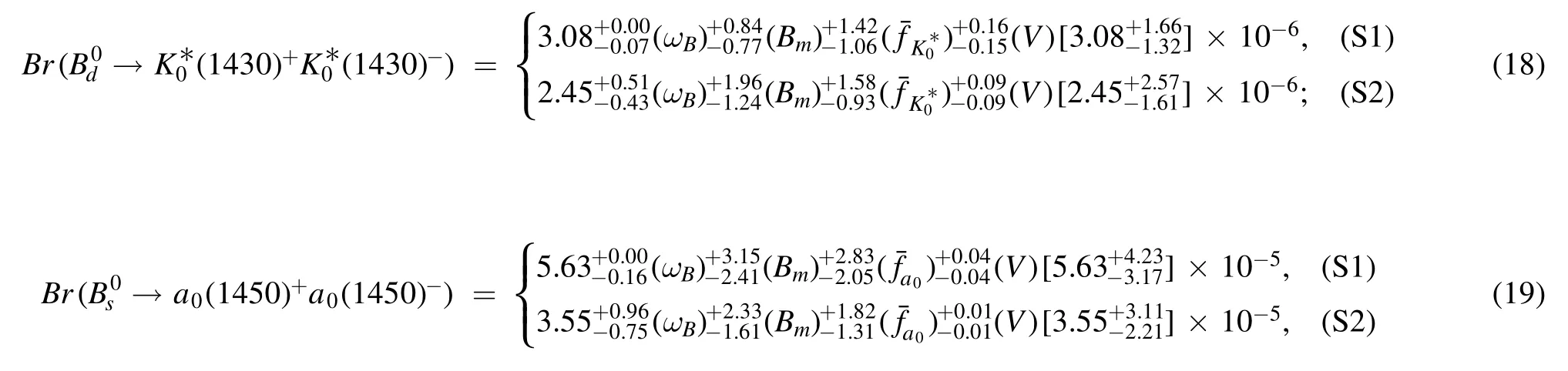
where, as clearly seen from the above results, the majored errors are mainly induced by the uncertainties of the scalar decay constantsandand the combined Gegenbauer moments Bmof B1and B3in the leading twist distribution amplitudes of the scalar mesons. The other errors induced by the shape parameter ωBin themeson distribution amplitude and by the combined CKM matrix elements V are much smaller. Frankly speaking, these mentioned hadronic parameters of the scalar mesons are currently less constrained from the experiments and/or Lattice QCD calculations. Therefore, we have to adopt those available parameters calculated in the QCD sum rule method to give a rough estimation preliminarily. Of course, both the essential measurements at the experimental aspects and the Lattice QCD computation at the theoretical aspects on the abovementioned nonperturbative inputs for the scalar mesons are urgently demanded, which is expected to help better understand the related hadron dynamics and provide more precise predictions. Note that all the errors from various parameters as specified above have been added in quadrature, which can be seen from the results presented in the square brackets.

Based on the numerical results with large theoretical uncertainties as shown in the equations (16)–(19), several remarks are in order:

(c) In light of the large theoretical errors,a precise ratio of the related branching ratios would be more interested because,generally speaking,the theoretical errors resulted from the hadronic inputs could be cancelled to a great extent.Therefore,we define the following ratios to be measured at the relevant experiments of B meson decays,which would help to study the QCD dynamics,even the decay mechanism of these considered pure annihilation decays.

Of course,it is found that the uncertainties in some of the above ratios are not small,for example,=in equation (22).The underlying reason is that the large uncertainties induced by the Gegenbauer moments B1and B3cannot be cancelled correspondingly,unlike the exact cancellation of the uncertainties resulted from the scalar decay constants that can be isolated from the distribution amplitudes.

(d) Another eight more interesting ratios could be obtained and are expected to be examined at the future experiments,if we take the already measuredandπ+π−decays as referenced channels.By combing the branching fractions of the→K+K−and→π+π−decays from both of the PQCD predictions[28] and the experimental measurements [24] sides,and the decay rates of theandmodes in this work,they are read as follows,

Table 1.The factorization decay amplitudes(in units of 10−3 GeV3)in S1 of the pure annihilation → and decays in the PQCD approach,where only the central values are quoted for clarifications.

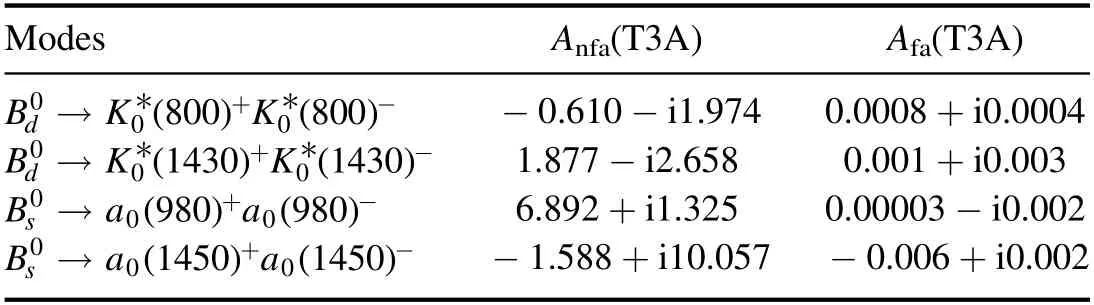
Table 1.The factorization decay amplitudes(in units of 10−3 GeV3)in S1 of the pure annihilation → and decays in the PQCD approach,where only the central values are quoted for clarifications.

Modes Anfa(T3A) Afa(T3A)() ()→+−B K 800K 800 d0 0 0* * −0.610 −i1.974 0.0008+i0.0004() ()→+−B K 1430K 1430 d0 0 0* * 1.877 −i2.658 0.001+i0.003()()→+−B a980a980s000 6.892+i1.325 0.00003 −i0.002() ()→+−B a1450a1450s000 −1.588+i10.057 −0.006+i0.002

and

These large values of the above ratios with still large theoretical errors could be easily tested when the related samples are collected with good precision experimentally.

(e) As mentioned in the above,the isospin symmetry breaking effects from the u and d quark masses have been considered in thedecays.Therefore,the factorizable annihilation decay amplitudes are not exact zero,which can be seen clearly from the numerical results as shown in the tables 1 and 2 in both scenarios S1 and S2.However,they are still tiny and could be neglected safely.It means that the contributions to the pure annihilation decays considered in this work are absolutely from the nonfactorizable annihilation decay amplitudes.It is noticed that,relative to theanddecays,the antisymmetric QCD behavior of the leading twist distribution amplitude could make the destructive interferences in the pseudoscalar sector become the constructive ones in the scalar sector to the nonfactorizable annihilation diagrams between the figure 1(c) with hard gluon radiating from light d(s) quark and the figure 1(d) with hard gluon radiating from heavy anti-b quark,which eventually result in the large CP-averaged decay rates of the considered decays,as presented in the equations (16)–(19).

Next,we will discuss the CP-violating asymmetries of theanddecays in the PQCD approach.Similar to the CP violations discussed in[39],we will present the direct and the mixing-induced CP violations Adirand Amixfor thedecays.While,except for Adirand Amix,the third CP asymmetryAΔΓsshould be considered simultaneously for thedecays because of the nonzero ratiofor themixing,where ΔΓ is the decay width difference of themeson mass eigenstates[51,52].Then the numerical results of the CP asymmetries Adir,Amix,evenAΔΓs4The definitions of Adir,Amix,andA ΔΓs are as followsrespectively,where the CPviolating parameterwith ηf being the CPeigenvalue of the final states.in the PQCD approach can be read as follows,

Table 2.Similar to table 1 but in S2 for the → (1 430)+ (1 430)−and →a0 (1 450)+ a0 (1 450)−decays.

Table 2.Similar to table 1 but in S2 for the → (1 430)+ (1 430)−and →a0 (1 450)+ a0 (1 450)−decays.

Modes Anfa(T3A) Afa(T3A) Anfa(T3G) Afa(T3G)() ()→+−B K 1430K 1430 d0 0 0* * −1.940+i0.188 −0.0005 −i0.0006 −1.617+i1.571 −0.028+i0.762() ()→+−B a1450a1450s000 5.038 −i6.778 −0.002+i0.000 06 4.851 −i6.812 0.006+i0.003

and

(b) For thedecays,

and

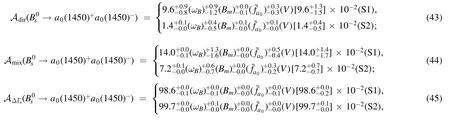
in which the Gegenbauer moments in the scalar meson distribution amplitudes and the parameters in the CKM matrix elements contribute to the majored errors theoretically,as clearly seen from the above equations (36)–(45).

Some comments are in order:

• It is clear to see that these predicted CP violations are generally insensitive to the variation of the scalar decay constantThe underlying reason is that the decay amplitudes of the considered decays are nearly proportional to the scalar decay constant,due to the vanishing vector decay constant(see equations(7)–(14)for detail)in the leading twist distribution amplitude [33],

?

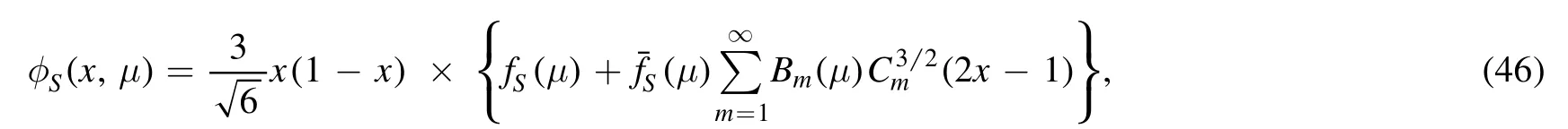
where fS(μ)andandare the vector and the scalar decay constants,the Gegenbauer moments,and the Gegenbauer polynomials,respectively,and the asymptotic forms of the twist-3 distribution amplitudes of the scalar a0andmesons.While,the CP asymmetries of thedecays are more sensitive to thethan those of theones to theThe fact is that the isospin symmetry breaking effect from the u and d quark masses leads to the tiny and negligible vector decay constanti.e.equation (13),and the SU(3) flavor symmetry breaking effect from the u and s quark masses results in the small but non-negligiblei.e.equation (11).

• It is easy to find that,apart from the Adiranda0(1 450)−)S2with few percent,the rest CP-violating asymmetries for the considered pure annihilation decays ofandin the PQCD approach are large,which means that the contributions from the penguin diagrams are generally sizable.To see this point explicitly,we present the decay amplitudes classified as the tree diagrams and the penguin ones,respectively,in the tables 3–4,where only the central values are quoted for clarifications.Then it is expected that these predictions of the CP violations,associated with the predicted large decay rates,could be confronted with the relevant experiments at LHCb and/or Belle-II in the (near) future.Of course,the Adirandare too small to be measured easily in the near future,though the corresponding branching ratios are as large as 10−5.

At last,we shall discuss the effects arising from the twist-3 distribution amplitudes of the scalar a0(1450) andmesons by including the Gegenbauer polynomials in S2,as mentioned in the above footnote 2.It is noted that the twist-3 distribution amplitudes with Gegenbauer polynomials of the scalar mesons in S2 have been investigated in[48],

with the Gegenbauer moments

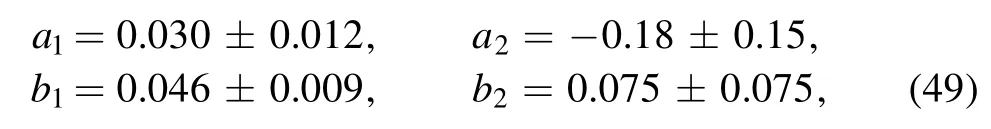
at μ=1 GeV for the1430)state,and

with the Gegenbauer moments

at μ=1 GeV for the a0(1450)state,respectively5It is necessary to mention that the Gegenbauer moments for the twist-3 distribution amplitudes of and a0(1450) states are originally presented as [48] (1) a1=0.018–0.042,a2=−0.33 to −0.025,b1=0.037–0.055,and b2=0–0.15 at μ=1 GeV for thestate,and (2) a2=−0.33 to −0.18,a4=−0.11 to 0.39,b2=0–0.058,and b4=0.070–0.20 for the a0(1450) state,respectively.To give the numerical results as central values with uncertainties,we adopt the form of the Gagenbauer moments in the twist-3 distribution amplitudes as presented in the equations (49) and (52) for convenience..Then,by including the contributions from these twist-3 distribution amplitudes,the numerical results for the branching ratios and the CP-violating asymmetries in S2 could be obtained asfollows,

Table 4.Similar to table 3 but in S2 for the → (1 430)+ (1 430)−and →a0 (1 450)+ a0 (1 450)−decays.

Table 4.Similar to table 3 but in S2 for the → (1 430)+ (1 430)−and →a0 (1 450)+ a0 (1 450)−decays.

Modes Tree diagrams(T3A) Penguin diagrams(T3A) Tree diagrams(T3G) Penguin diagrams(T3G)() ()→+−B K 1430K 1430 d0 0 0* * ()− −+1.081 i 1.178 0.129 i 1.593 ()− +− +0.859 i 1.365 1.574 i 0.352 ()− +−0.566 i 0.658 0.850 i 0.171 ()− +− +1.079 i 1.675 1.949 i 0.415() ()→+−B a1450a1450 s000 ()− −+0.328 i 0.048 0.229 i 0.239 ()−−5.364 i 6.730 5.364 i 6.730 ()− +−0.097 i 0.188 0.192 i 0.088 ()−−4.954 i 6.998 4.954 i 6.998

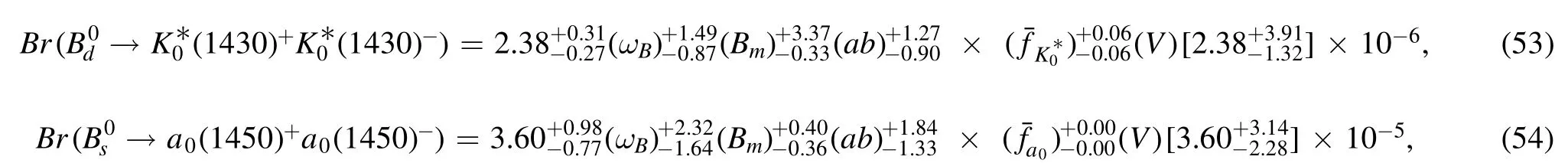
in which the central value of the branching fractionbecomes slightly smaller[larger] than that obtained in the case with adopting the asymptotic form of the twist-3 distribution amplitudes correspondingly.Of course,the CP-averaged branching ratios almost remain unchanged within the still large theoretical errors.And

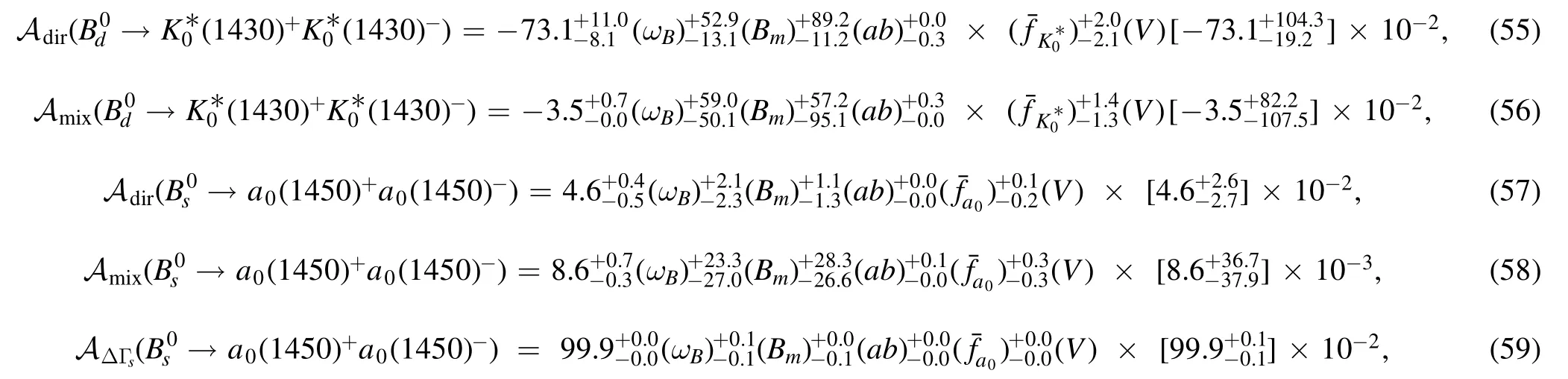
where the direct CP-violating asymmetry and the mixing-induced one are changed significantly for theand→a0(1 450)+a0(1 450)−decays in S2.Note that the parameter (ab) in the above equations (55)–(59) denotes the combined Gegenbauer moment of aiand biin the twist-3 distribution amplitudes with Gegenbauer polynomials.In terms of the central value,the Adirvaries from 21.4% in the T3A form to −73.1% in the T3G form for the former mode,while from 1.4%in the T3A form to 4.6%in the T3G form for the latter one;and the Amixchanges from −97.5% to −3.5% for the former channel,while from 7.2% to 0.86% for the latter one,which indicate that the strong phases in these two pure annihilation decays could be dramatically affected by the twist-3 distribution amplitudes with inclusion of the Gegenbauer polynomials.In order to show the significant changes of the mentioned strong phases,we present the decay amplitudes of these two pure annihilation modes,i.e.andin S2 explicitly by considering the twist-3 distribution amplitudes in the T3A and T3G forms respectively,as given in the tables 2 and 4.It is clearly seen that the magnitudes of the dominant contributions from the nonfactorizable annihilation diagrams vary slightly,but the strong phases in both of the factorizable and nonfactorizable annihilation diagrams change remarkably,which means that the considered T3G contributions are also important to the strong phases in the annihilation diagrams of this work.Therefore,the clear understanding of the hadron dynamics about the scalar mesons considered in this work could be very helpful to provide precise predictions theoretically,even to explore the presently unknown annihilation decay mechanism.

In short,it is well known that the annihilation diagrams,although which are power suppressed and with currently unknown mechanism,could play important roles in the heavy flavor B and D meson decays.As one of the popular tools theoretically,the PQCD approach has the advantages in computing the annihilation contributions.Therefore,by assuming the scalar a0andbeing themesons in two different scenarios,we have investigated the CP-averaged branching ratios and the CP-violating asymmetries for the pure annihilation decays ofandin the PQCD approach,which embrace the same quark structure asandin the pseudoscalar sector.At the same time,for theand→a0(1 450)+a0(1 450)−decays,we also studied the contributions from the twist-3 distribution amplitudes in the Gegenbauer polynomial forms of the1 430)and a0(1450) in S2.Based on the numerical results within still large theoretical errors and the phenomenological analyses,the predictions in the PQCD approach showed that:

• The large decay rates in the order of 10−6and 10−5have been obtained in the PQCD calculations for the pure annihilationanddecays,respectively,but which suffer from large theoretical uncertainties mainly arising from the hadronic parameters of the scalar a0andmesons,such as the Gegenbauer moments,the scalar decay constants,etc.Undoubtedly,these large predictions in the PQCD approach could be examined at the LHCb and/or Belle-II experiments in the (near) future.

• The unknown inner structure or QCD dynamics of the scalar states demands the reliable studies from the experimental examinations,or in the nonperturbative techniques,for example,Lattice QCD.The clear understanding about the QCD dynamics of the scalars must constrain the errors of the predictions in the PQCD approach of the pure annihilation modes in this work,which would provide opportunities to shed light on the mechanism of the annihilation decays.

Acknowledgments

Y Chen thanks L Su for helpful discussions.This work is supported in part by the National Natural Science Foundation of China under Grant Nos.11765012 and 11 205 072,and by the Research Fund of Jiangsu Normal University(No.HB2016004).Y C is supported by the Undergraduate Research & Practice Innovation Program of Jiangsu Province (No.201810320103Z).