Spectral Solutions of Linear and Nonlinear BVPs Using Certain Jacobi Polynomials Generalizing Third- and Fourth-Kinds of Chebyshev Polynomials
W.M.Abd-Elhameedand Asmaa M.Alkenedri
1Department of Mathematics,Faculty of Science,Cairo University,Giza,Egypt
2Department of Mathematics,College of Science,University of Jeddah,Jeddah,Saudi Arabia
ABSTRACT This paper is dedicated to implementing and presenting numerical algorithms for solving some linear and nonlinear even-order two-point boundary value problems.For this purpose,we establish new explicit formulas for the high-order derivatives of certain two classes of Jacobi polynomials in terms of their corresponding Jacobi polynomials.These two classes generalize the two celebrated non-symmetric classes of polynomials,namely,Chebyshev polynomials of third-and fourth-kinds.The idea of the derivation of such formulas is essentially based on making use of the power series representations and inversion formulas of these classes of polynomials.The derived formulas serve in converting the even-order linear differential equations with their boundary conditions into linear systems that can be efficiently solved.Furthermore,and based on the first-order derivatives formula of certain Jacobi polynomials,the operational matrix of derivatives is extracted and employed to present another algorithm to treat both linear and nonlinear two-point boundary value problems based on the application of the collocation method.Convergence analysis of the proposed expansions is investigated.Some numerical examples are included to demonstrate the validity and applicability of the proposed algorithms.
KEYWORDS Jacobi polynomials;high-order boundary value problems;Galerkin method;collocation method;connection problem;convergence analysis
1 Introduction
It is well-known that the Chebyshev polynomials play vital roles in the scope of mathematical analysis and its applications.The first- and second-kinds are special symmetric polynomials of the Jacobi polynomials,so they are ultraspherical polynomials.These two kinds of Chebyshev polynomials are the most popular kinds,and they are employed extensively in numerical analysis,see for example[1–4].There are other four kinds of Chebyshev polynomials.Third- and fourthkinds are also special kinds of Jacobi polynomials,but they differ from the first- and second-kinds since they are not ultraspherical polynomials.In fact,they are non-symmetric Jacobi polynomials with certain parameters.There are considerable publications devoted to investigating these kinds of polynomials from both theoretical and practical points of view.For some articles in this direction,one can be referred to[5–7].Fifth- and sixth-kinds of Chebyshev polynomials are not special cases of the Jacobi polynomials.These polynomials were first established by Jamei in his Ph.D.dissertation[8].Recently,these kinds of polynomials have been employed for treating numerically some types of differential equations,see[9–11].
Spectral methods are essential in numerical analysis.These methods have been utilized fruitfully for obtaining numerical solutions of various kinds of differential and integral equations.The philosophy in the application of spectral methods is based on writing the desired numerical solution in terms of certain “basis functions,” which may be expressed as combinations of various orthogonal polynomials.There are three celebrated spectral methods;they are tau,collocation,and Galerkin methods.Galerkin method is based on choosing suitable combinations of orthogonal polynomials satisfying the underlying boundary/initial conditions[12].Tau method is more flexible than the Galerkin method due to the freedom in choosing the basis functions.Collocation method is the most popular method because of its capability to treat all kinds of differential equations.There are considerable contributions employ this method in different types of differential equations[13–15].For a survey on spectral methods and their applications,one can consult[16–21].
The problems of establishing derivatives and integrals formulas of different orthogonal polynomials in terms of their original polynomials are of great interest.These formulas play important parts in obtaining spectral solutions of various differential equations.For example,the authors in[5,6]derived explicit formulas of the high-order derivatives and repeated integrals of Chebyshev polynomials of third- and fourth-kinds,and after that,they utilized the derived formulas for obtaining spectral solutions of some boundary value problems(BVPs).
Boundary value problems have important roles due to their appearance in almost all branches related to applied sciences such as engineering,fluid mechanics,and optimization theory(see,[22]).Some examples concerning applications of BVPs are given with details in[22].Moreover,the author showed that,at some times,it is more appropriate to transform high-order BVPs into systems of differential equations.Many real-life phenomena can be described by high-order BVPs.
Regarding the even-order BVPs,they arise in numerous problems.The free vibrations analysis of beam structures is governed by a fourth-order ordinary differential equation[23].The vibration behavior of a ring structures is governed by a sixth-order ordinary differential equation[24].Eighth-order BVPs arise in torsional vibration of uniform beams[25].In addition,10th- and 12th-orders appear in applications.When a uniform magnetic field is applied across the fluid in the same direction as gravity.Ordinary convection and overstability yield a 10th-order and a 12th-order BVPs,respectively[26].For applications regarding the high-order BVPs appear in hydrodynamic and hydromagnetic stability,fluid dynamics,astronomy,beam and long wave theory[27,28].For some other applications of these kinds of problems,one can be referred to[29–31].
Several studies were performed for the numerical solutions of these types of equations.Some of the algorithms treat these kinds are the perturbation and homotopy perturbation methods in[32],differential transform methods in[26]and spectral methods in[15,33–37].
The main objectives of this article can be summarized in the following items:
• Deriving high-order derivatives formulas of certain classes of polynomials that generalize Chebyshev polynomials of the third- and fourth-kinds.
• Implementing and analyzing an algorithm for the numerical solutions of even-order linear BVPs based on the application of the spectral Galerkin method.
• Introducing a collocation algorithm for treating both linear and nonlinear BVPs.
The current paper is organized as follows.In Section 2,we give some relevant properties of Jacobi polynomials.In Section 3,we derive in detail two new formulas which give explicitly the high-order derivatives of Jacobi polynomials whose parameters difference is one.In Section 4,we present a spectral Galerkin algorithm for solving some high even-order linear BVPs with constant coefficients.Section 5 is devoted to presenting another algorithm for treating linear and nonlinear BVPs based on the application of a suitable collocation algorithm.Section 6 is interested in solving the connection problem between certain Jacobi polynomials and the Legendre polynomials.In Section 7,we investigate the convergence and error analysis of the proposed expansion in Section 5.In Section 8,we present some numerical examples including comparisons with some other methods to ascertain the accuracy and efficiency of the proposed algorithms presented in Sections 4 and 5.Finally,some conclusions are reported in Section 9.
2 Some Fundamental Properties of Jacobi Polynomials
The classical Jacobi polynomials,is a polynomial of degreemwhich can be defined in hypergeometric form as
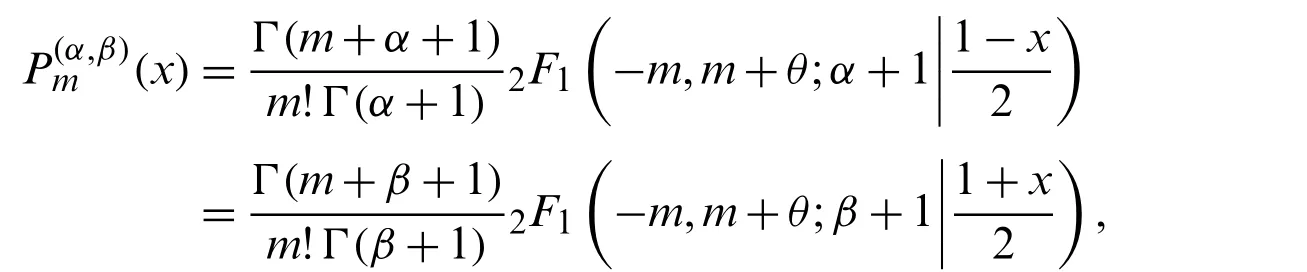
where
θ=α+β+1.
It is easy to see the following special values

It is desirable to define the normalized orthogonal Jacobi polynomials as[38]

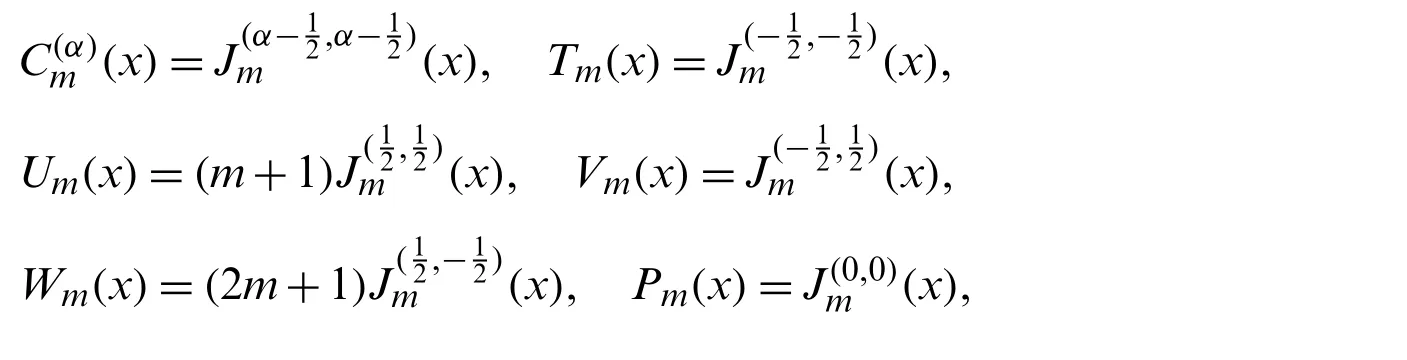
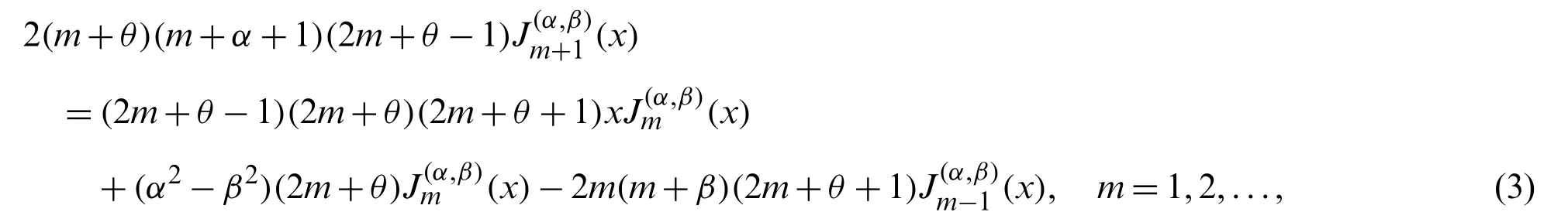
with the initial values:
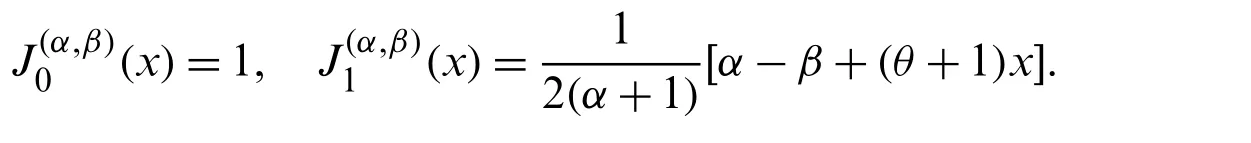
The orthogonality relation satisfied byis given by:
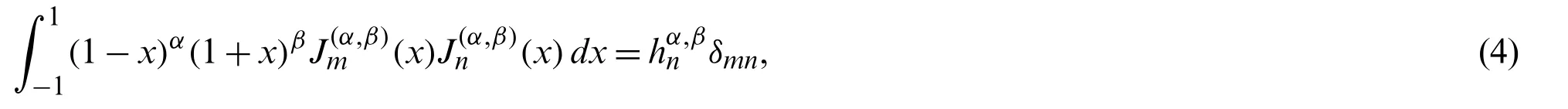
whereδmnis the well-known Kronecker delta function,and
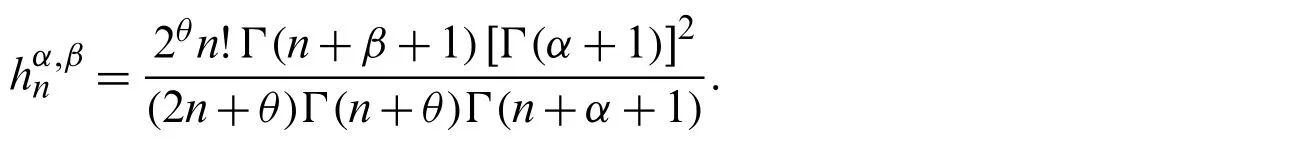
The special values
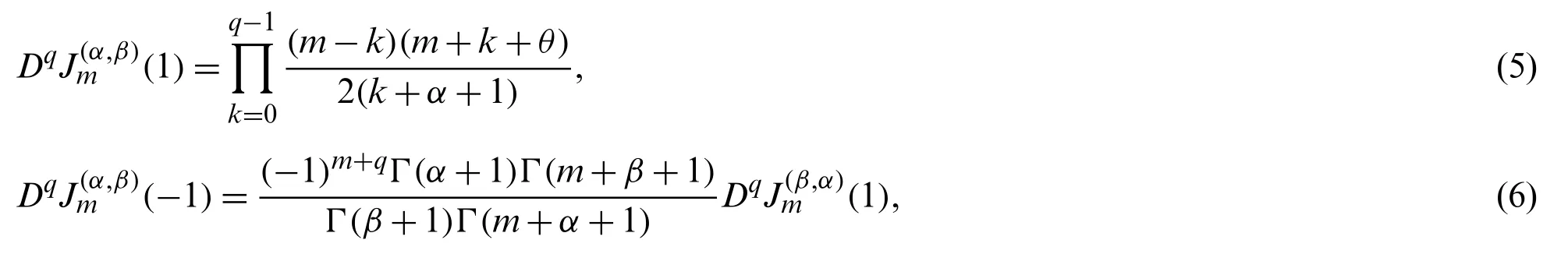
will be of important use later.
It is useful to extend the Jacobi polynomials on a general interval[a,b].In fact,the shifted Jacobi polynomials can be defined on[a,b]by

Hence,properties and relations concerned with the Jacobi polynomialscan be easily transformed to give their counterparts for the shifted polynomials.
For our upcoming computations,we need the orthogonality relation ofon[a,b].This relation is given explicitly as:
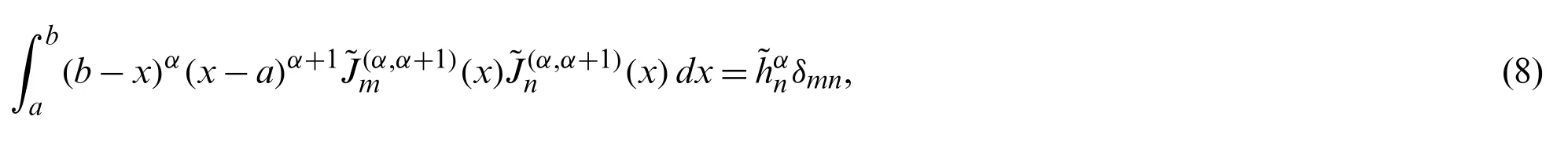

3 The qth Derivative of
The main objective of this section is to state and prove two theorems which express the highorder derivatives of the shifted Jacobi polynomialsandin terms of their original polynomials.The basic idea behind the derivation of the desired formulas is built on employing the power form representation and the inversion formula of the Jacobi polynomials.Now,the following three lemmas are essential in this regard.
Lemma 3.1.The explicit power form of the normalized Jacobi polynomialsis given by

where
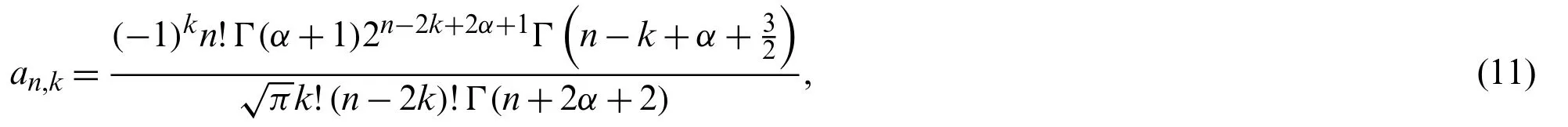
and
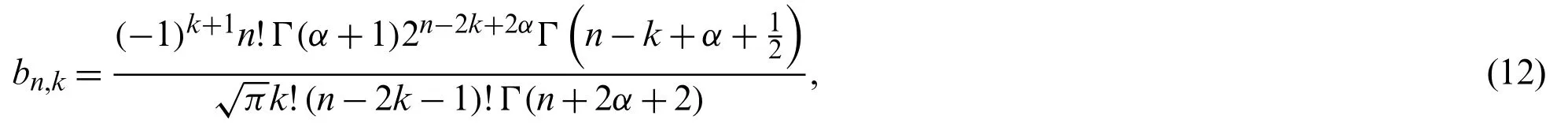
where[z]represents the largest integer less than or equal toz.
Proof.We proceed by induction onn.Assume that relation(10)is valid for(n−1)and(n−2),and we have to prove the validity of(10)itself.Starting with the recurrence relation(3),(for the caseβ=α+1)in the form
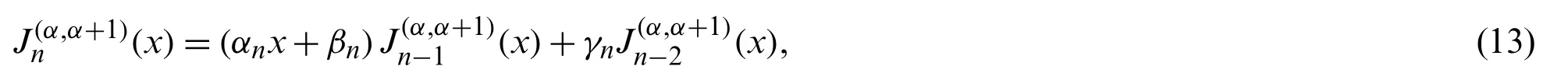
where
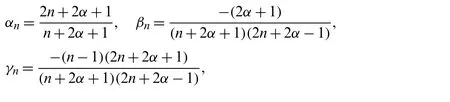
then,the application of the induction hypothesis twice yields
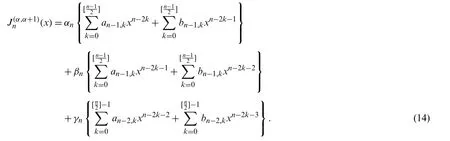
Eq.(14)may be written in the form

where
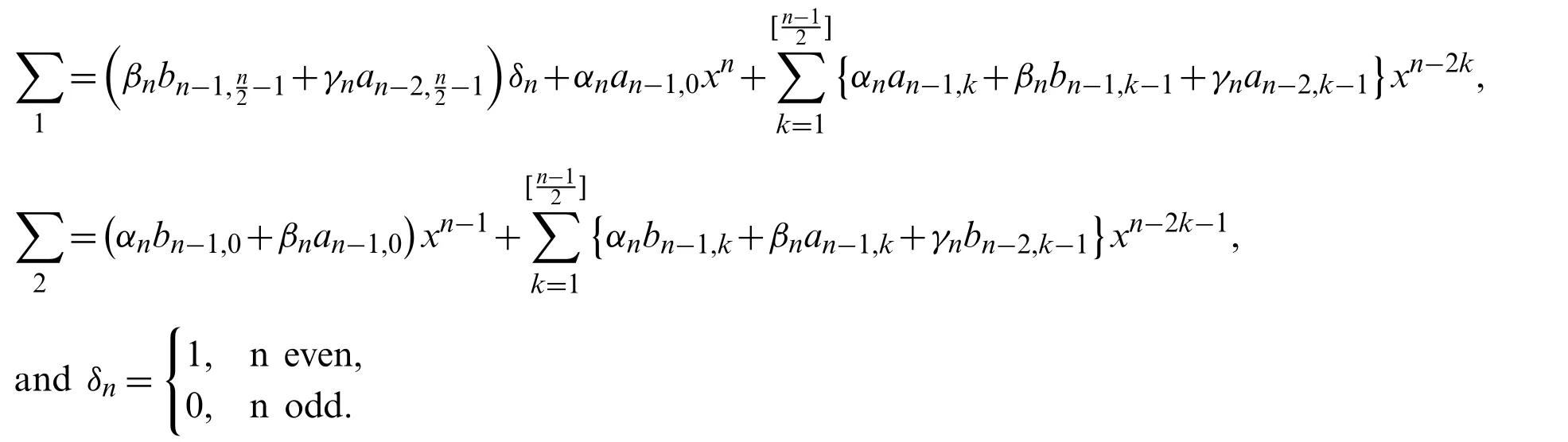
It is not difficult to see that
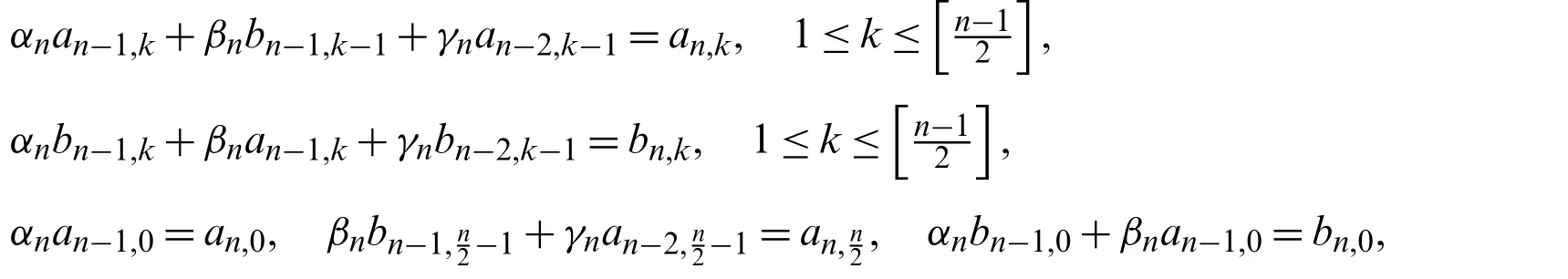
wherean,k,bn,kare given by(11)and(12),respectively.Therefore

and

and this completes the proof of formula(10).
Lemma 3.2.For all,the following inversion formula holds

where
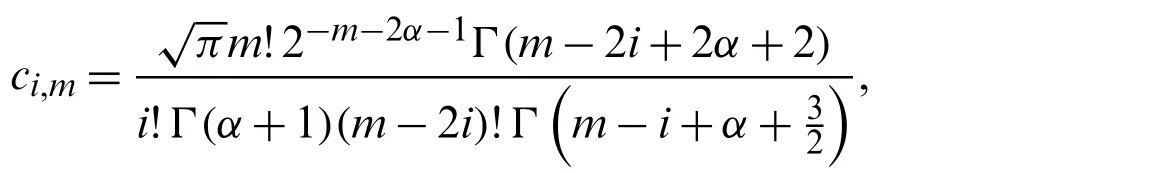
and
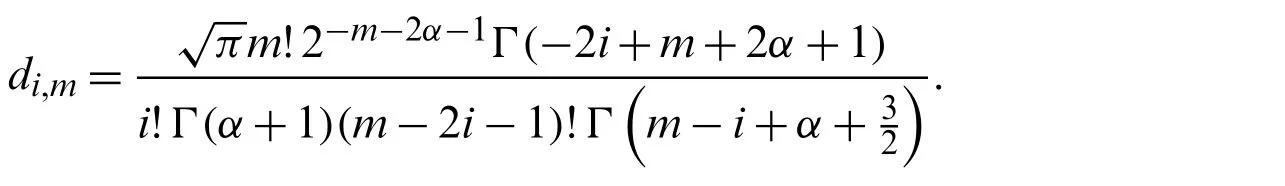
Proof.We proceed by induction onm.Form=1,the left-hand side equals the right-hand side.Assume that relation(15)is valid,and we have to show that

Multiplying both sides of relation(15)byx,then with the aid of relation(3),(for the caseβ=α+1),and after some rather manipulation,Eq.(16)can be proved.
Lemma 3.3.For every nonnegative integerm,we have
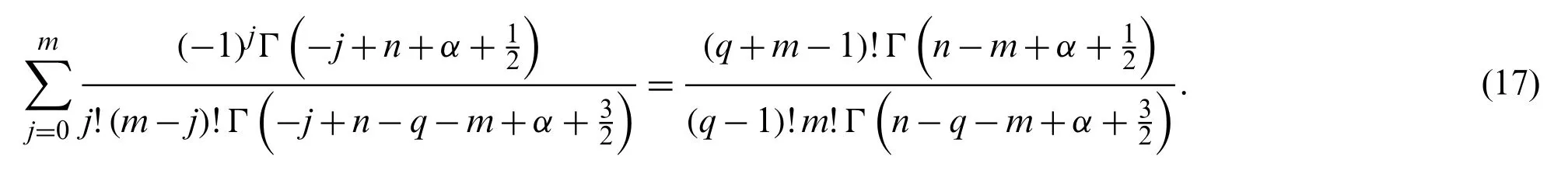
Proof.If we set

then,with the aid of Zeilberger’s algorithm[39],Sn,q,msatisfies the following first-order recurrence relation:
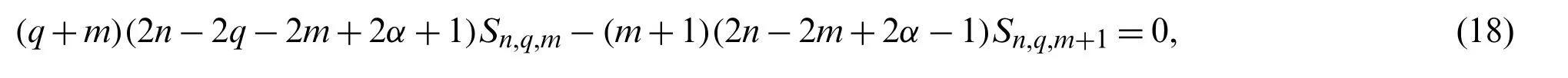
with the initial value

The exact solution for this recurrence relation is
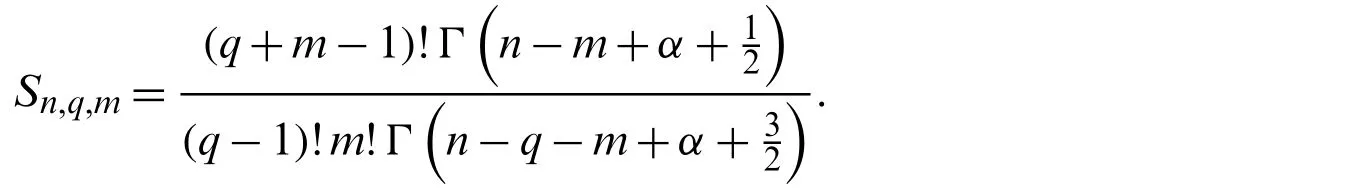
This proves Lemma 3.3.
Now,we are in a position to state and prove the desired derivatives formula.
Theorem 3.1.The derivatives of the normalized shifted Jacobi polynomialsof any degree and for any order in terms ofare given explicitly by
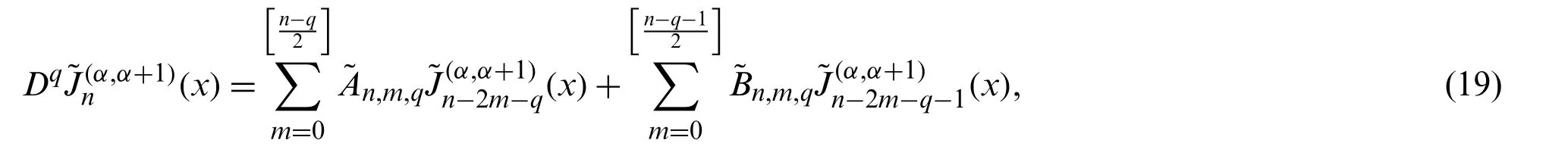
where
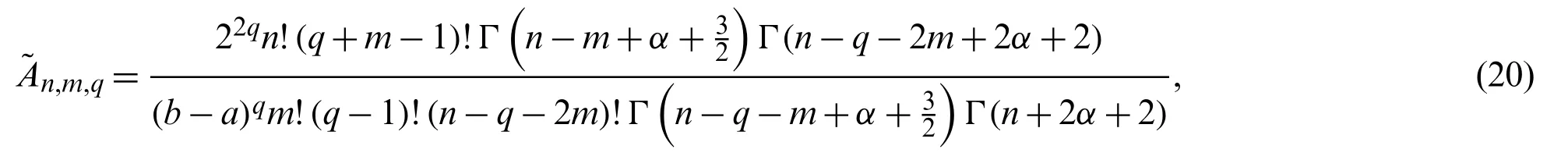
and
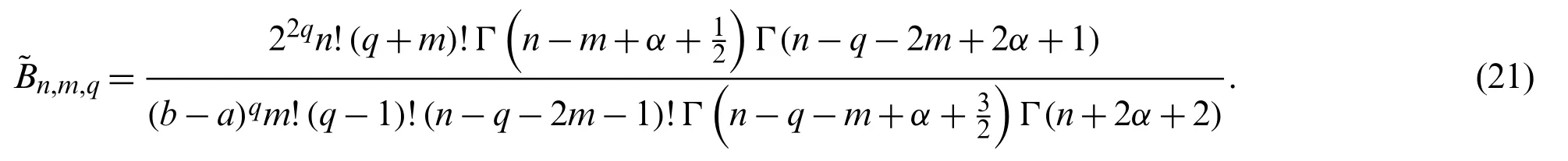
Proof.We prove the theorem for[a,b]≡[−1,1],that is,we prove the following formula:

where
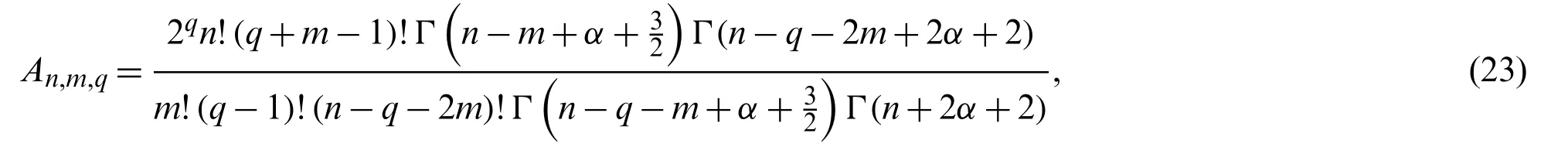
and
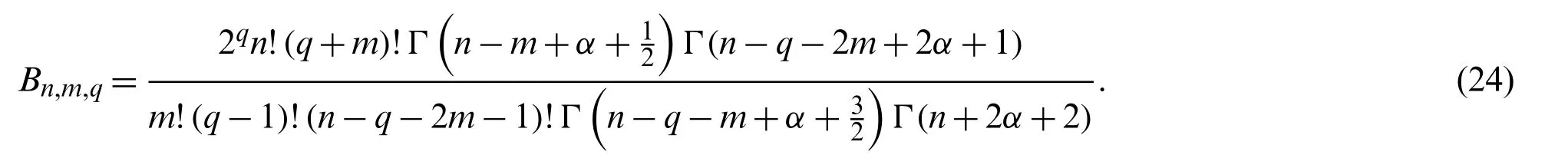
If we differentiate Eq.(10)q-times with respect tox,and noting the identity

then,we get
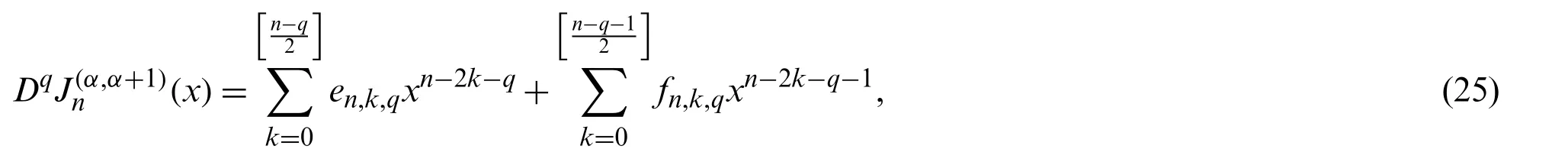
where

Making use of relation(15),enables one to write

where
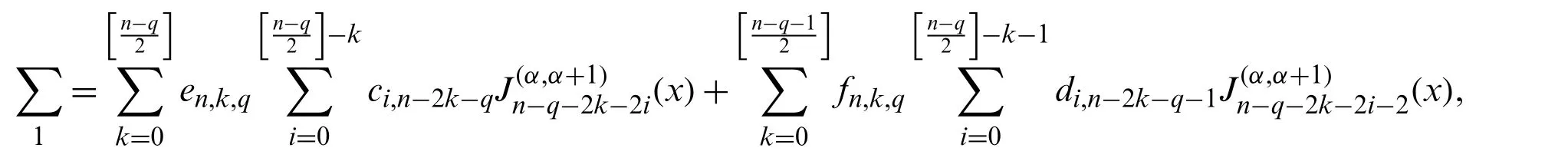
and
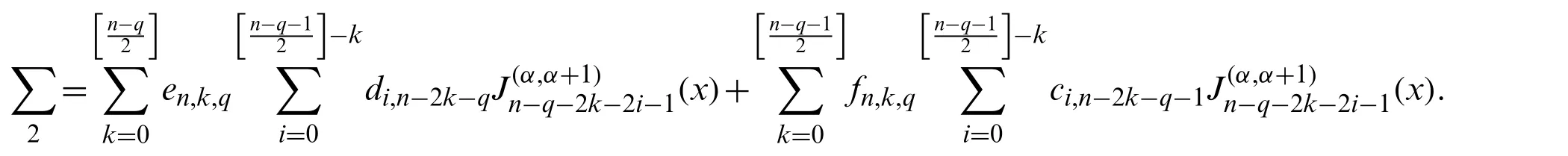
we get
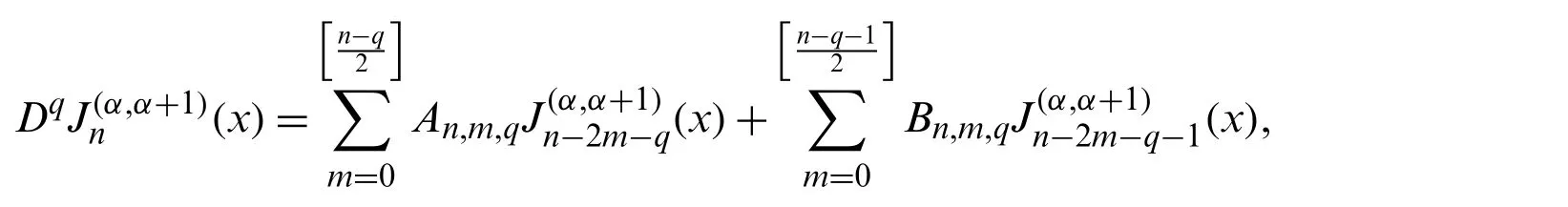
where
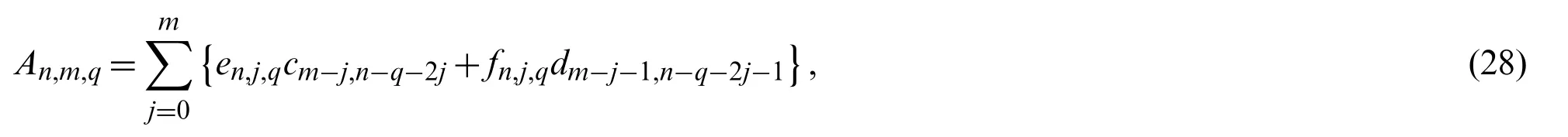
and
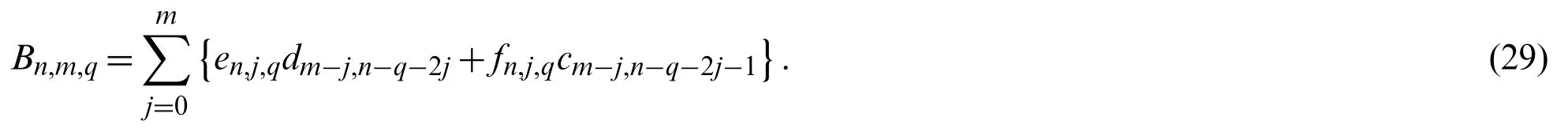
Now,it is not difficult to show that

and
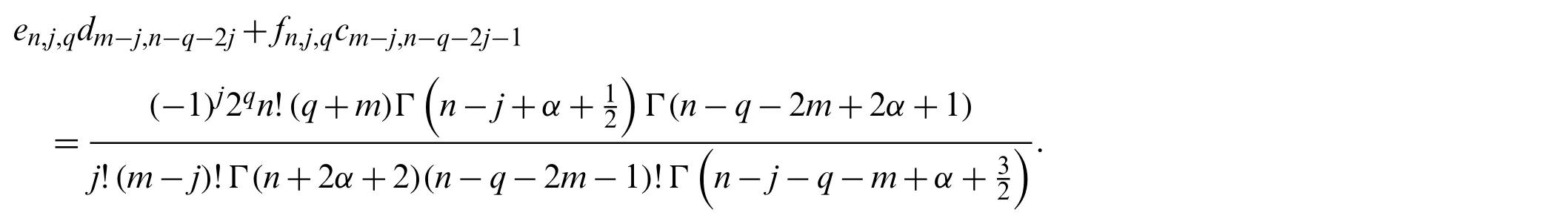
Finally,making use of Lemma 3.3,An,m,qandBn,m,qtake the forms
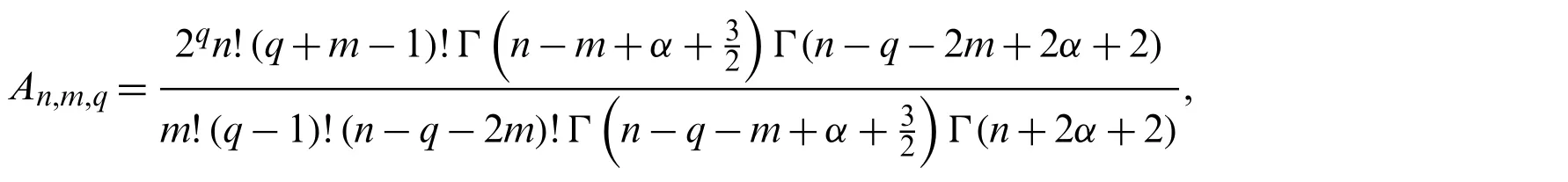
and
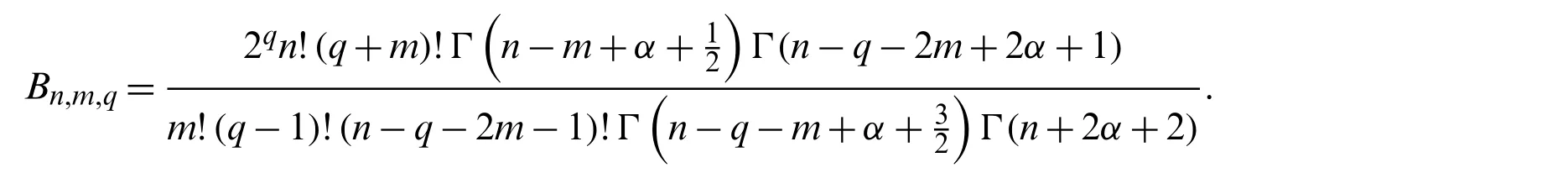
Replacingxin(22)byformula(19)can be obtained.This completes the proof of Theorem 3.1.
Remark 3.1.It is to be noted here that relation(19)may be written in the alternative form

where
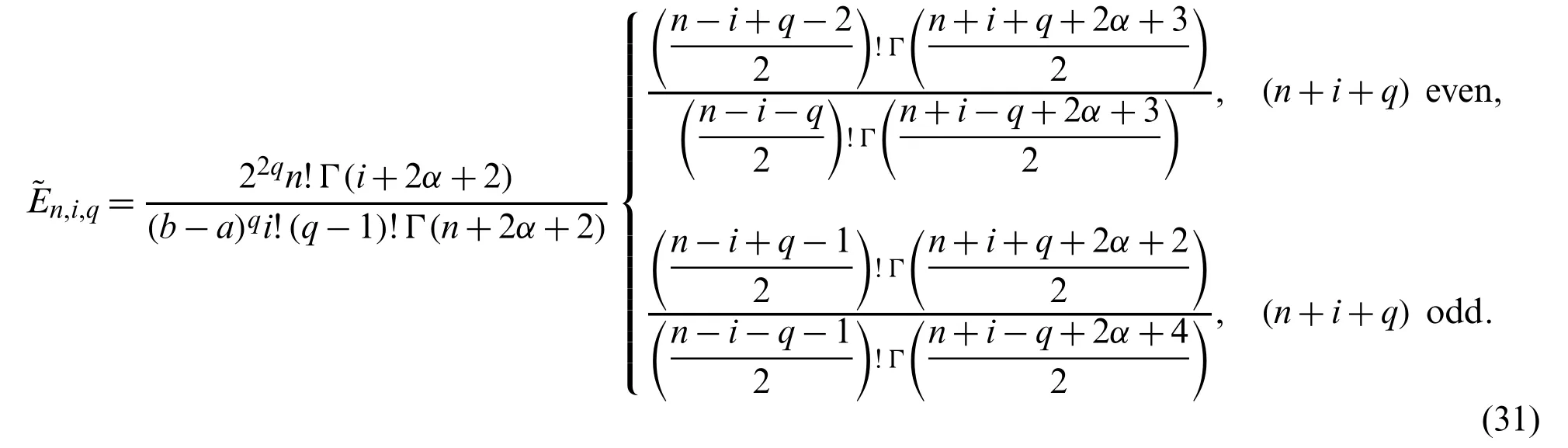
Remark 3.2.As a direct consequence of relation(30),theqth derivative ofcan be easily deduced.This result is given in the following theorem.
Theorem 3.2.The derivatives of the normalized Jacobi polynomialsof any degree and for any order in terms ofare given explicitly by
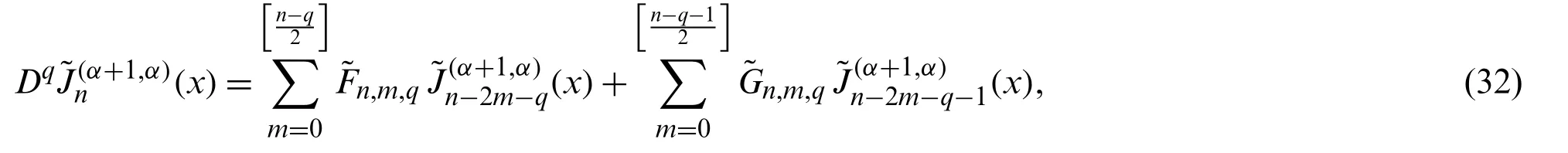
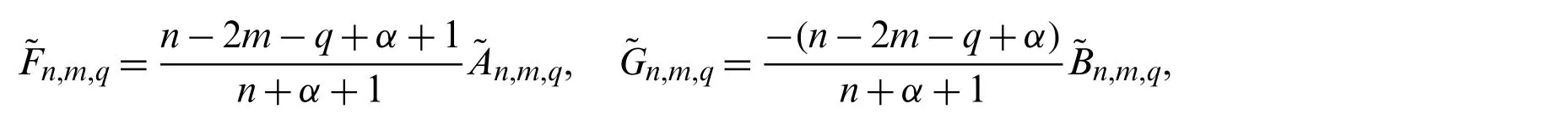

where

As two direct consequences of Theorems 3.1 and 3.2,the formulas for the high-order derivatives of Chebyshev polynomials of third- and fourth-kinds in terms of their corresponding Chebyshev polynomials can be deduced.These results are given in the following two corollaries.
Corollary 3.1.The derivatives of Chebyshev polynomials of third-kindVn(x)on[−1,1]of any degree and for any order in terms of their original polynomials are given by the following explicit formula:
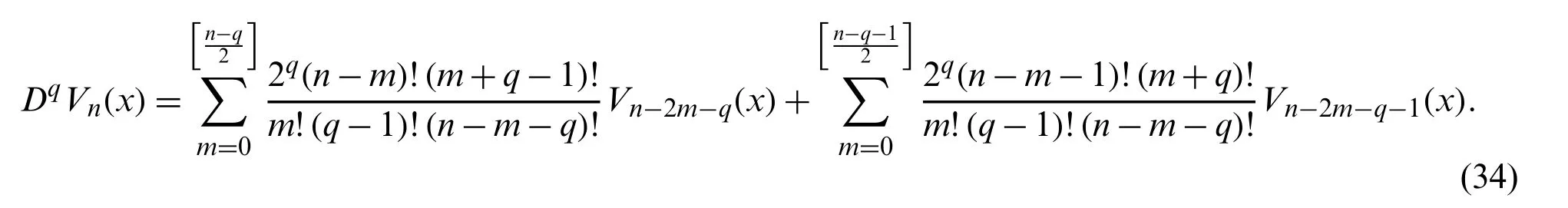
Corollary 3.2.The derivatives of Chebyshev polynomials of fourth-kindWn(x)on[−1,1]of any degree and for any order in terms of their original formulas are given by
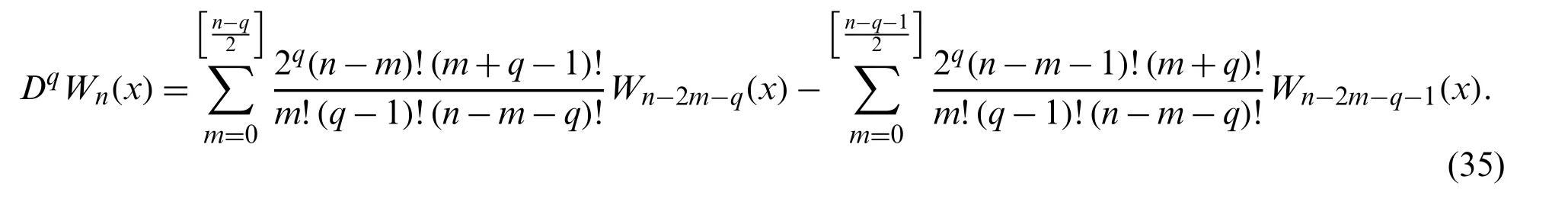
Remark 3.3.The results of Corollaries 3.1 and 3.2 are in complete agreement with those obtained in[6].
Remark 3.4.From now on,we will employ only the polynomialsand their shifted oneswhich will be denoted,respectively,byand.All corresponding results using the polynomialsand their shifted onescan be obtained similarly.
4 The Solution of High Even-Order Differential Equations Using
This section is confined to analyzing in detail a spectral Galerkin algorithm for treating numerically even-order BVPs.We will employ the shifted Jacobi polynomials.
Now,consider the following even-order BVPs:

governed by the boundary conditions:


The philosophy of applying the Galerkin method to solve(36)–(37)is based on choosing basis functions satisfying the boundary conditions(37),and after that,enforcing the residual of Eq.(36)to be orthogonal to these functions.Now,if we set
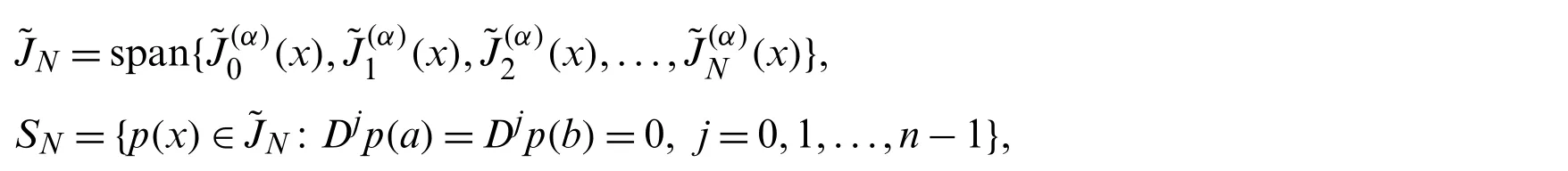
then,to apply the shifted Jacobi–Galerkin method for solving(36)–(37),we have to findsuch that

wherew(x)=(b−x)α(x−a)α+1,andis the scalar inner product in the weighted space.
4.1 The Choice of Basis Functions
In this section,we describe how to choose suitable basis functions satisfying the boundary conditions(37)to be able to apply the Galerkin method to(36)–(37).The idea for choosing compact combinations satisfying the underlying boundary conditions was first introduced in[40,41].In these two papers,the author selected suitable basis functions satisfying the standard secondand fourth-order BVPs which are considered as special cases of(36).The basis functions were expressed in terms of Chebyshev polynomials of the first-kind and Legendre polynomials.The authors in[42]generalized the proposed algorithms in[40,41].They suggested compact combinations of ultraspherical polynomials that generalize the Chebyshev of the first-kind and Legendre combinations to solve the even-order BVPs in one- and two-dimensions.The authors in[43]solved the same types of BVPs but by using certain kinds of non-symmetric Jacobi polynomials which are called Chebyshev polynomials of the third- and fourth-kinds.In this section,we are going to generalize the basis functions that derived in[43].
First,consider the case[a,b]≡[−1,1],and set
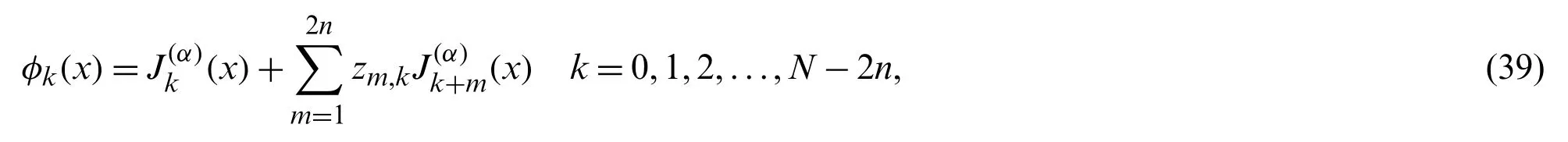
where the coefficients {zm,k}are chosen such that every member of {φk(x)}verifies the following homogeneous boundary conditions:

It is not difficult to see that the boundary conditions(40)along with(39)after making use of identities(5)and(6),(for the caseβ=α+1),lead to the following system of equations in the unknowns {zm,k}:
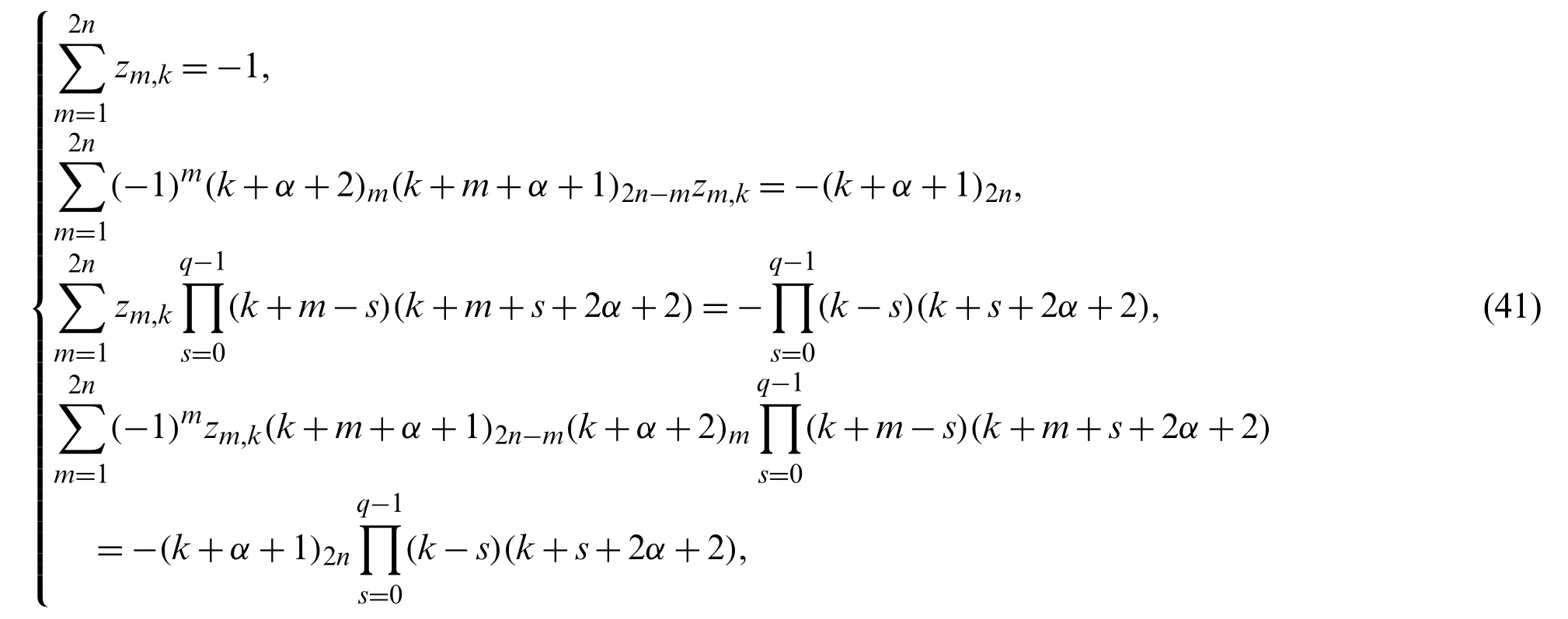
wherek=0,1,...,N−2n,andq=1,2,...,n−1.
The determinant of the above system is different from zero,hence {zm,k} can be uniquely determined to give
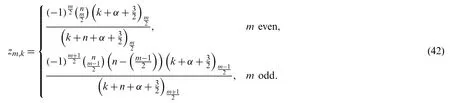
and hence the basis functionstake the form:
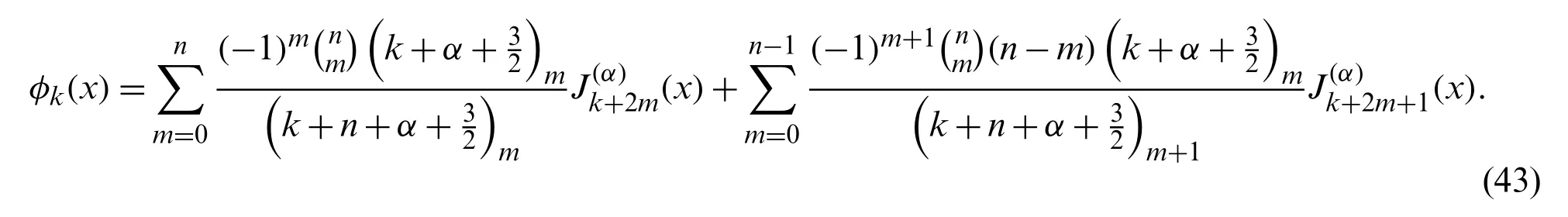
Remark 4.1.Ifxin(39)is replaced by,then it is easy to see that the basis functions take the form
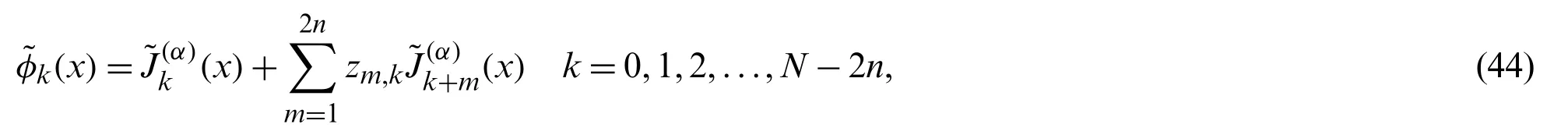
and from(43),we see that they have the following explicit expression
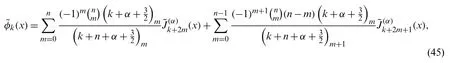
satisfies the following boundary conditions
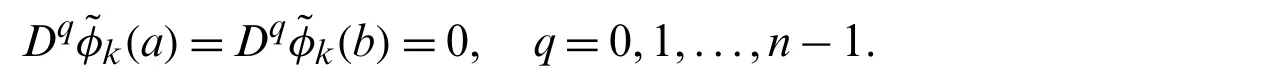
Remark 4.2.If we choose the basis functions in terms of the general parameters normalized Jacobi polynomials,that is
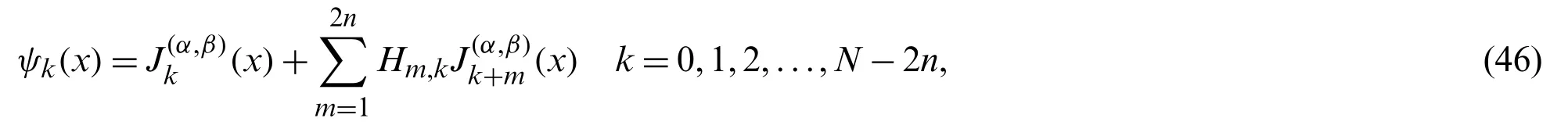
then,the resulting linear system to be solved to find the coefficientsHm,kcan not be found in simple forms free of hypergeometric forms except for special choices of their parameters.The choiceβ=α+1 in this paper enables one to get the simple form of the basis functions in(43).
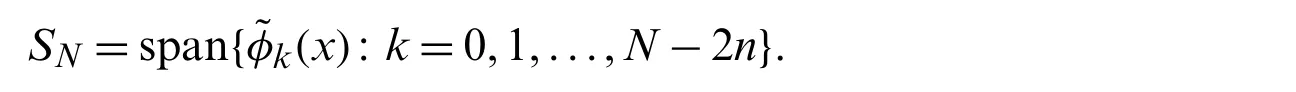
Now,denote
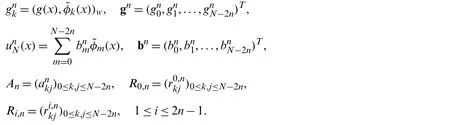
Then Eq.(38)can be transformed into the following matrix system

and the entries of the matricesAnandRi,n,(0 ≤i≤2n−1),are given explicitly in the following theorem.
Theorem 4.1.Let the family of basis functionsbe as taken in(44).Setting.Then,
and the nonzero elements of the matricesAn,Ri,n(1 ≤i≤2n−1)andR0,nare given explicitly by:

where
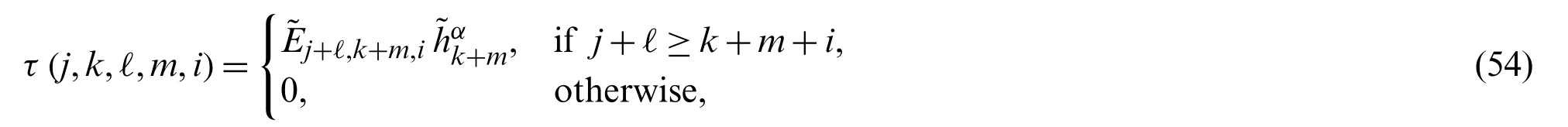
Proof.The nonzero elements of the matricesAn,Ri,n(1 ≤i≤2n−1)can be obtained with the aid of the derivatives formula(19).Substitutingq=2nin relation(30),yields


and,accordingly,relation(44)enables one to express the elementsin the form

In particular,it is easy to see that the diagonal elements ofAncan be simplified to give
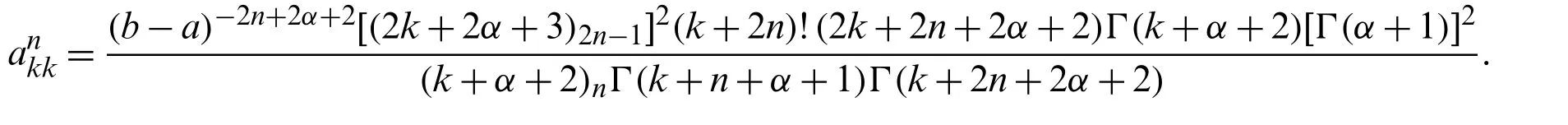
Regrading the elements of the matricesRi,n,(1 ≤i≤2n−1),we have
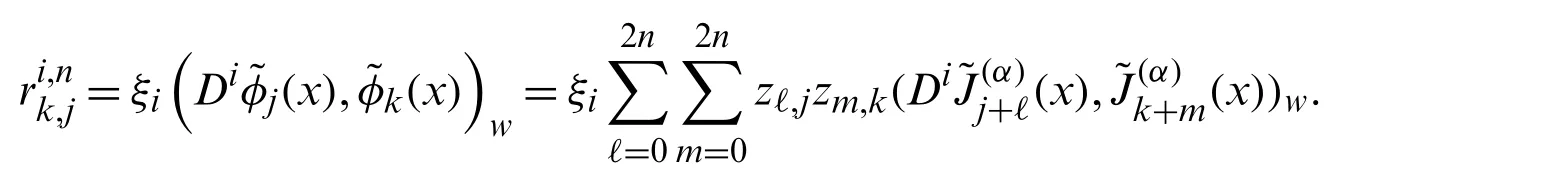
Using relation(30)and the orthogonality relation(8),can be computed to give formulas(50)–(52).Finally,regarding the elements of the matrixR0,n,we have
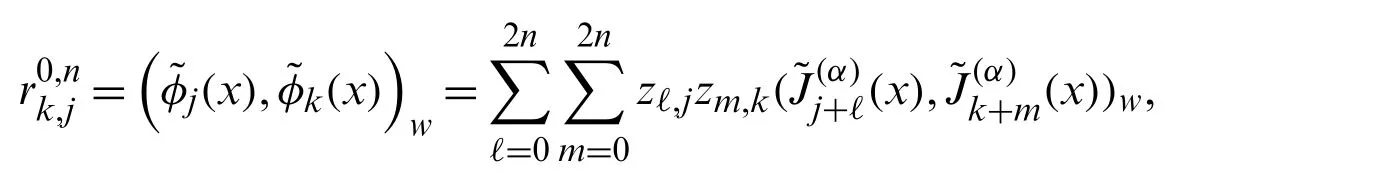
using the orthogonality relation(8),it can be shown that,forj=k+p,|p|≤2n,

This ends the proof of Theorem 4.1.
The special case corresponding to the choice:ηi=0,0 ≤i≤2n−1,is of interest.In such case,the system in(47)reduces to a linear system with nonsingular upper triangular matrix for all values ofn.The following corollary exhibits this result.
Corollary 4.1.For the case corresponds toηi=0,0 ≤i≤2n−1,the system in(47)reduces toAnbn=gn,whereAnis an upper triangular matrix,and its solution can be given explicitly as
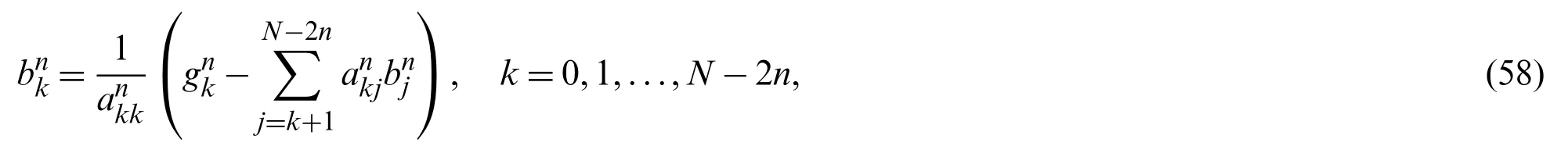
Remark 4.3.The following even-order BVP
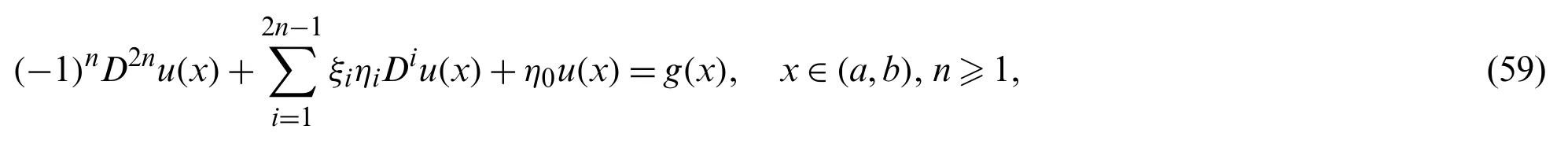
governed by the nonhomogeneous boundary conditions:

can be transformed to a modified one governed by homogeneous boundary conditions(see[43]).
5 A Collocation Algorithm for Treating Nonlinear BVPs
In this section,we implement and present a numerical algorithm based on a collocation method to solve even-order nonlinear BVPs.The basic idea is based on employing the operational matrix of derivatives of the shifted Jacobi polynomials.First,the following corollary is essential in the sequel.
Corollary 5.1.The first derivative of the polynomialscan be written explicitly as

where
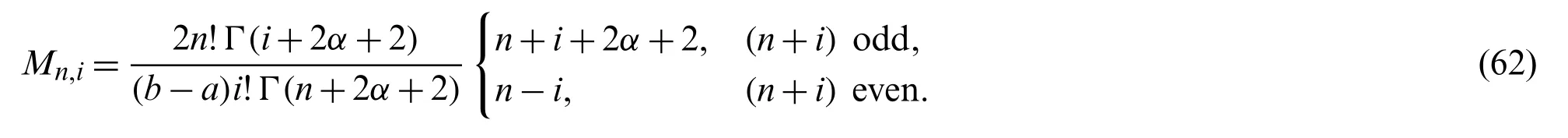
Proof.Direct from Eq.(30),settingq=1.
Now,if we define the following vector

then,it is easy to see that

whereMis the operational matrix of derivatives whose entries are defined as:
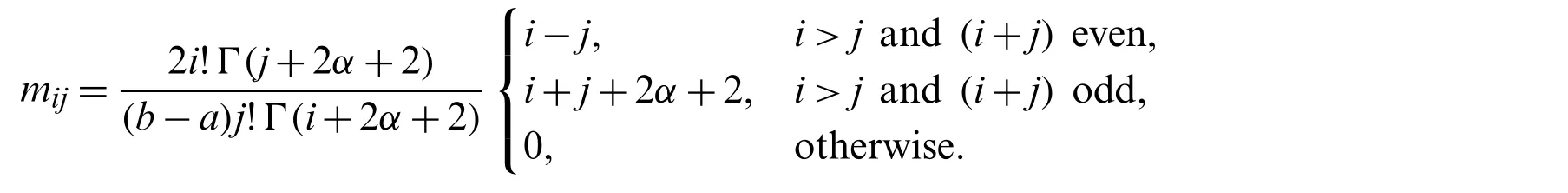
Now,consider the following nonlinear even-order BVPs:
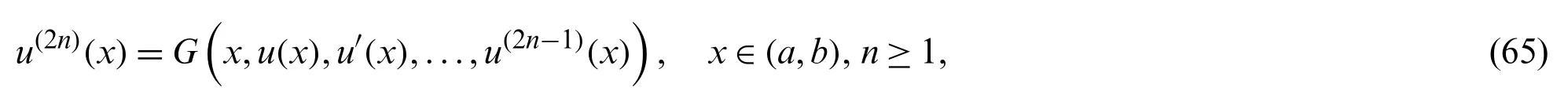
subject to the first-kind of boundary conditions:

or the second-kind of boundary conditions:

Now,consider an approximate solution of the form

This approximate solution can be expressed as

where

andΨ(x)is defined in(63).
In virtue of Eq.(64),it is easy to express theℓth-derivative ofuN(x).In fact,we can write

Based on relation(71),the residual of Eq.(65)can be written as
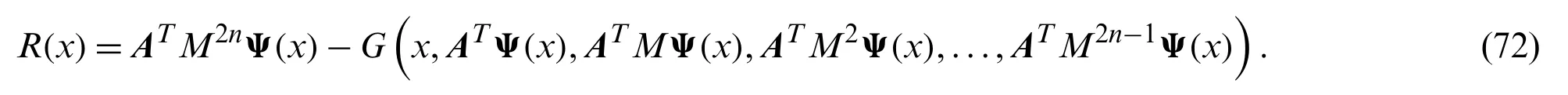
Now,for the sake of obtaining a numerical solution of(65),a collocation method is applied.More precisely,the residual in(72)is enforced to vanish at suitable collocation points.We choose them to be the distinct zeros of the polynomialthat is we have

Furthermore,the boundary conditions(66)yield the following(2n)equations:

while,the boundary conditions(67)yield the following(2n)equations:

Merging the(N+1)equations in(73)–(75),or the(N+1)equations in(73),(76)and(77),we get a nonlinear system in the expansion coefficientsakwhich can be solved with the aid of Newton’s iterative method.Thus an approximate solutionuN(x)can be found.
6 Connection Formula between the Polynomials and the Shifted Legendre Polynomials
This section is confined to present the connection formula between the polynomialsand the shifted Legendre polynomials on[a,b].This connection formula will be of important interest in investigating the convergence and error analysis in the subsequent section.To this end,the following theorem which links between two different parameters Jacobi polynomials is needed.
Theorem 6.1.For every nonnegative integern,the following connection formula holds:
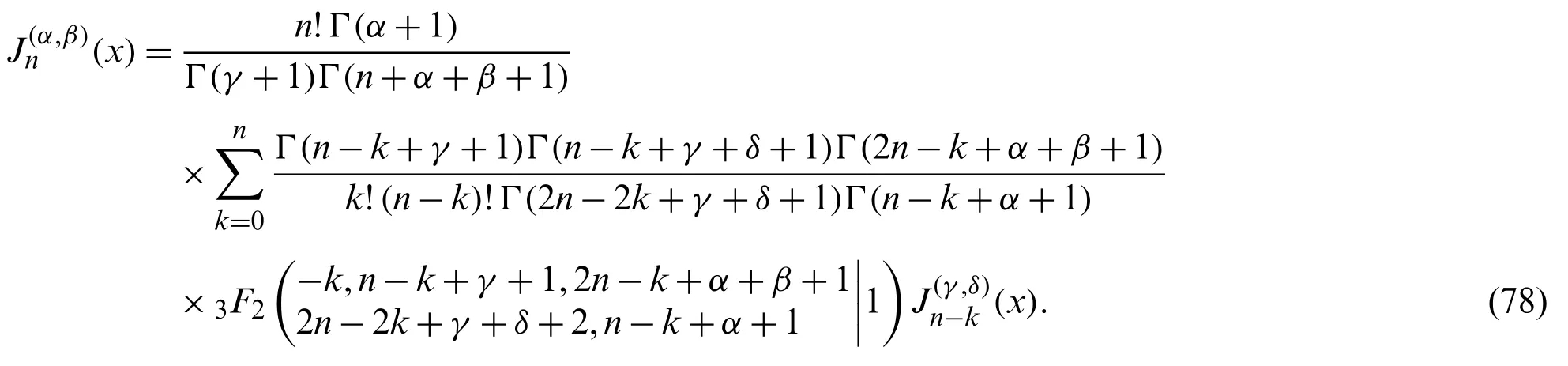
Proof.The connection formula between two different parameters classical Jacobi polynomials is given by[44]
with
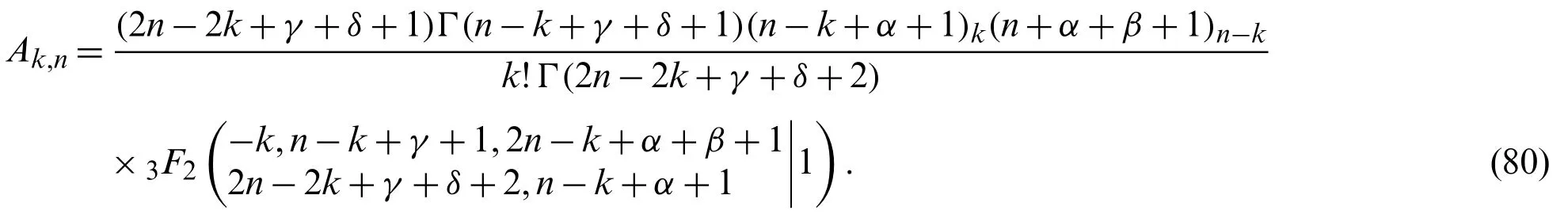
Taking into consideration relation(2),the connection formula(78)can be obtained.
Lemma 6.1.Letmandnbe two nonnegative integers.The following reduction formula holds
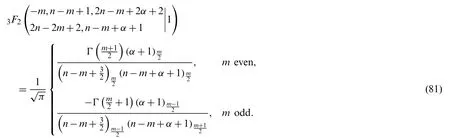
Proof.If we set
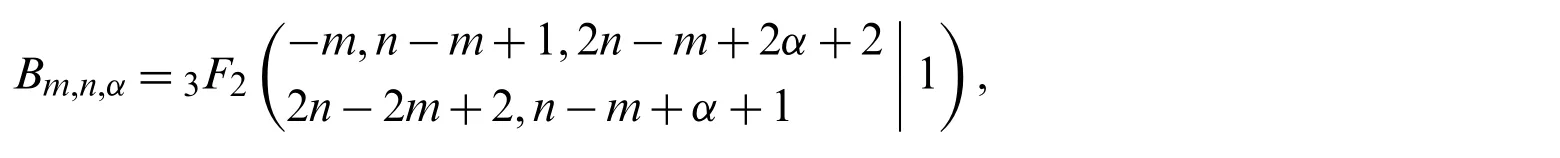
then,with the aid of Zeilberger’s algorithm,it can be shown that the following second-order recurrence relation is satisfied byBm,n,α
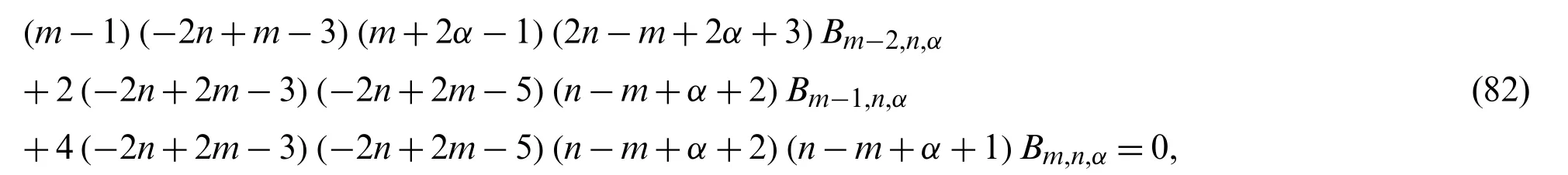
with the initial values

The recurrence relation(82)can be solved exactly to give
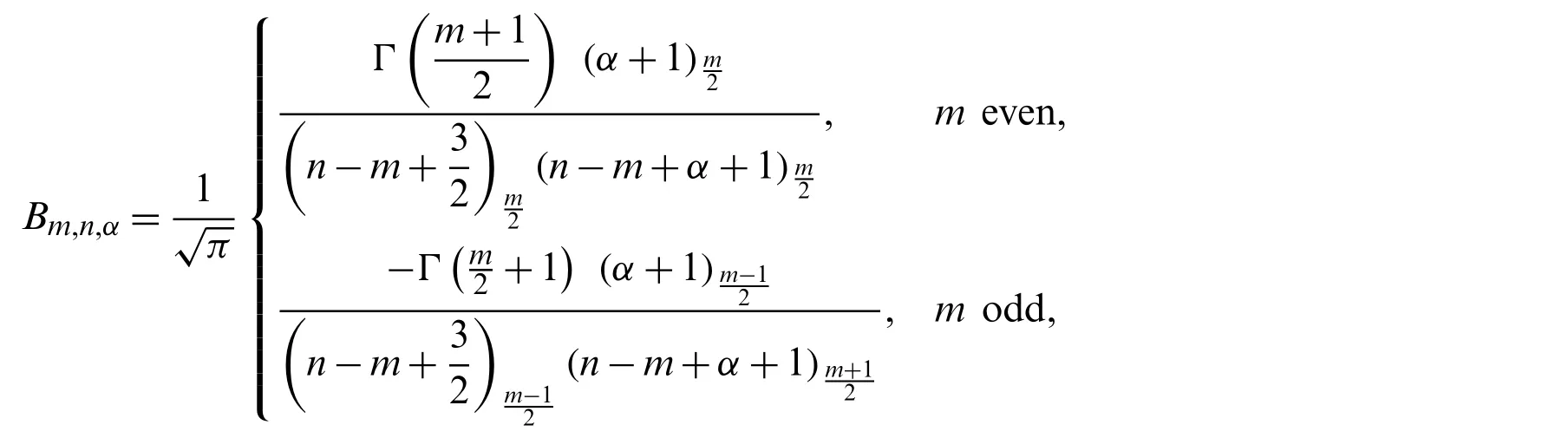
and,therefore,the reduction formula(81)can be followed.
Now,we are going to state and prove an important theorem that concerns the connection formula betweenand the shifted Legendre polynomials.
Theorem 6.2.The connection formula between the shifted normalized Jacobi polynomialsand the shifted Legendre polynomialscan be written explicitly in the form

where the connection coefficientsSk,n,αare given by
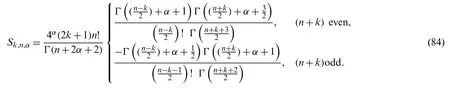
Proof.To prove the connection formula(83)with coefficients in(84),we prove first the formula on[−1,1],that is,we prove the formula

The last relation can be written alternatively in the form
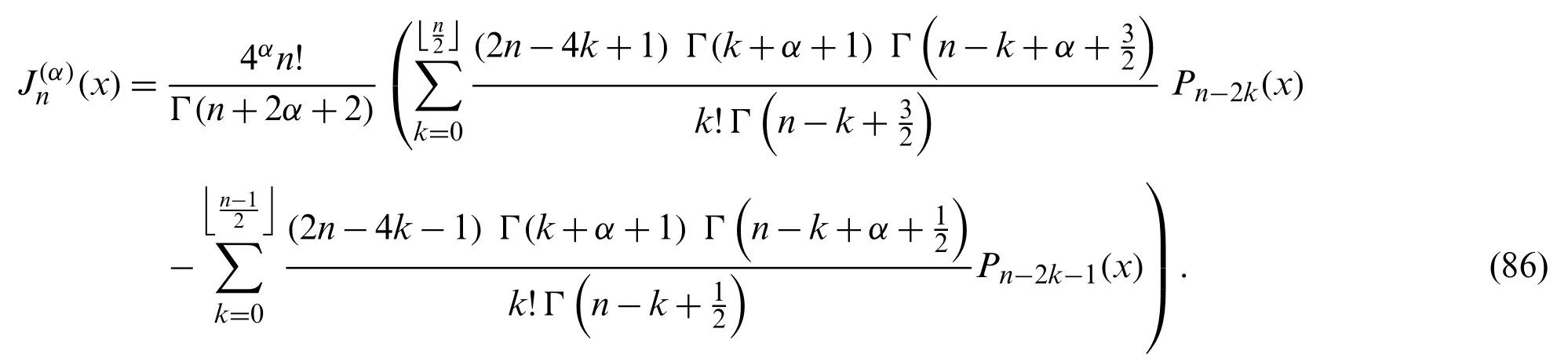
Settingβ=α+1 andγ=δ=0 in Eq.(78)yields the following formula
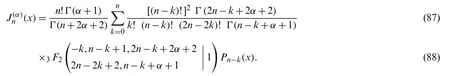
If we make use of Lemma 6.1,then the last formula,after some computations can be transformed into the form in(86),and therefore,relation(85)is proved.Replacingxbyin(85)gives(83).Theorem 6.2 is proved.
7 Study of the Convergence and Error Analysis
In this section,we state and prove some results concerning the convergence analysis of the proposed expansions in Sections 4 and 5.First,we mention some theoretical prerequisites.The following lemmas and theorems are needed.Let us agree on the following notation:For two positive sequencesai,bi,we say thatif there exists a generic constantcsuch thatai≤cbi.
7.1 Prerequisites
Lemma 7.1.Reference[45]Letdenote theq-times repeated integrals of shifted Legendre polynomials,that is

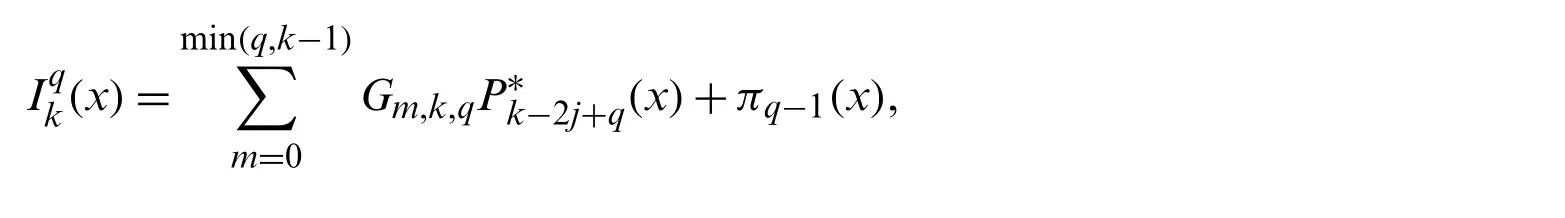
whereπq−1(x)is a polynomial of degree at most(q−1),and the coefficientsGm,k,qare given explicitly by

Lemma 7.2.Letbe defined as in the above lemma.The following estimate holds.
Proof.The lemma can be proved with the aid of the repeated integrals formula in Lemma 7.1 and noting the well-known inequality:.
Lemma 7.3.The connection coefficients in the connection problem(83),which expressed explicitly in(84)satisfy the following estimate

Proof.The result can be easily followed from the explicit formula of the connection coefficients in(84).
Lemma 7.4.For allx∈[a,b],the following estimate is valid

Proof.From the connection formula(83),and noting that,we get

We will prove(89).We consider the proof ifnis even.The case ifnis odd can be treated similarly.From(90),we can write
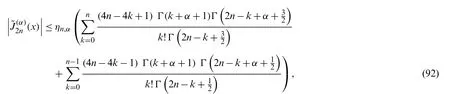
with

With the aid of Zeilberger’s algorithm,it is not difficult to show that
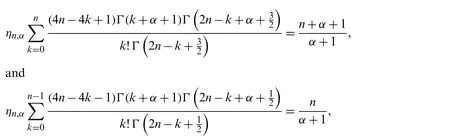
and accordingly,we get

The proof is now complete.
7.2 Convergence Analysis
Now,we are ready to state and prove some lemmas and theorems concerning the convergence of the truncated approximate solutions and the estimate for the truncation error of the proposed expansions in Sections 4 and 5.We first prove our results for the proposed expansion in Section 5.Assume that the exact and approximate expansions are respectively as follows:

and

From now on,and for more convenience,let us agree on the following notations:
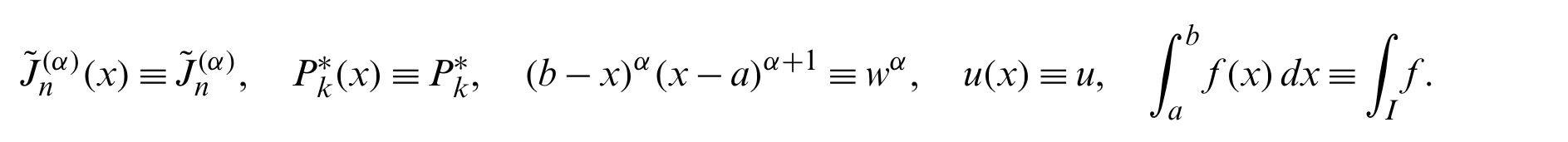
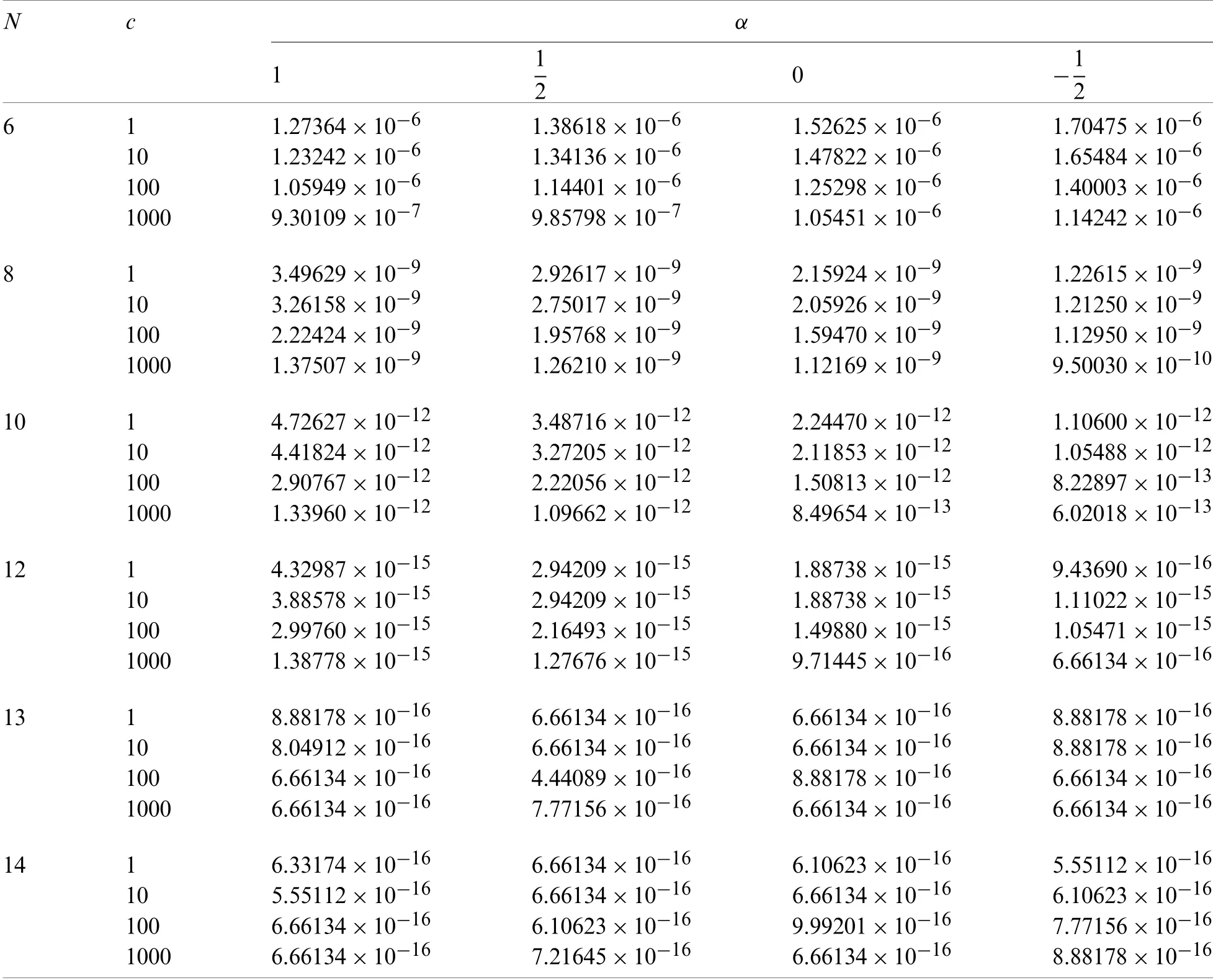
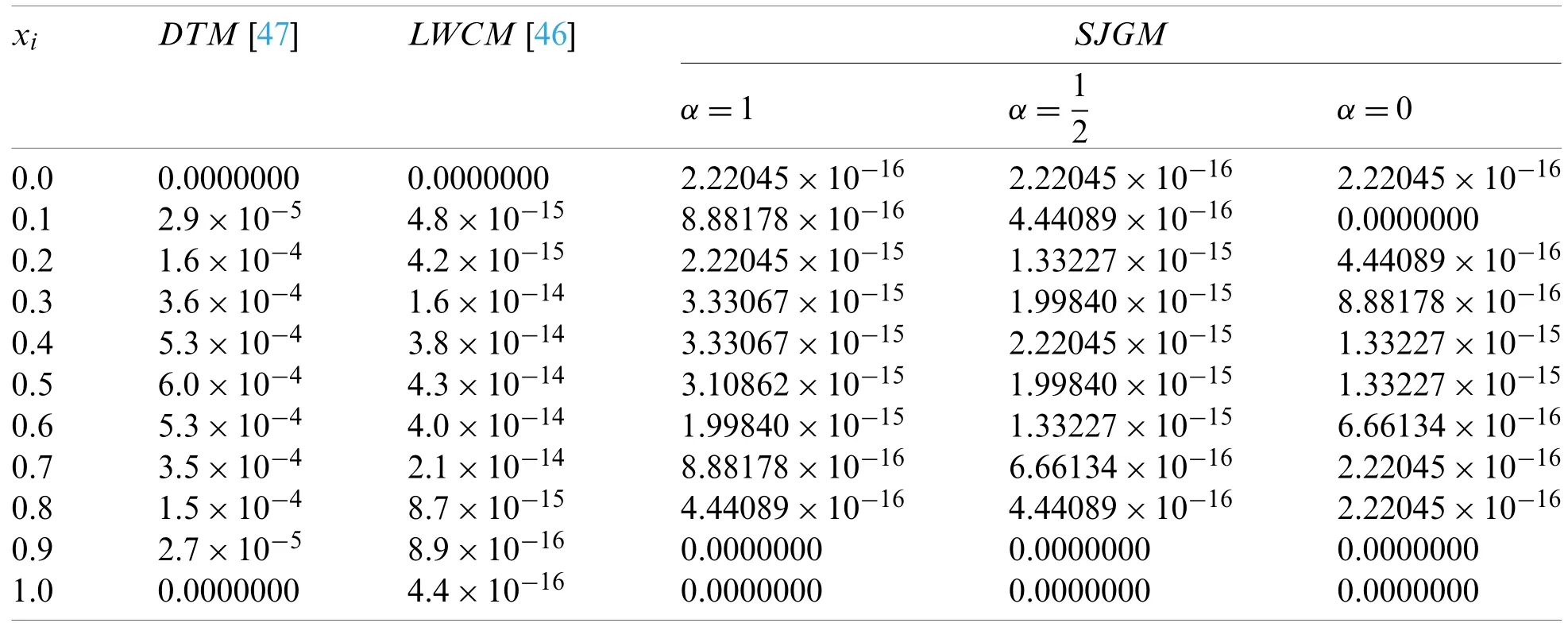
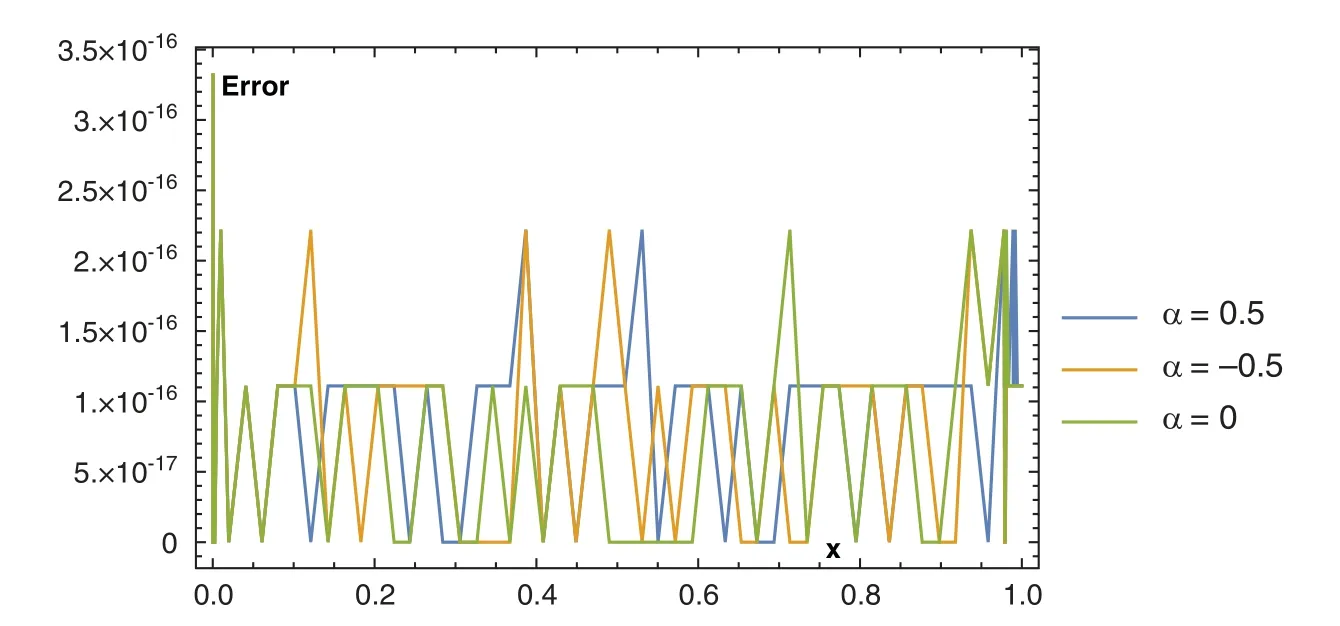
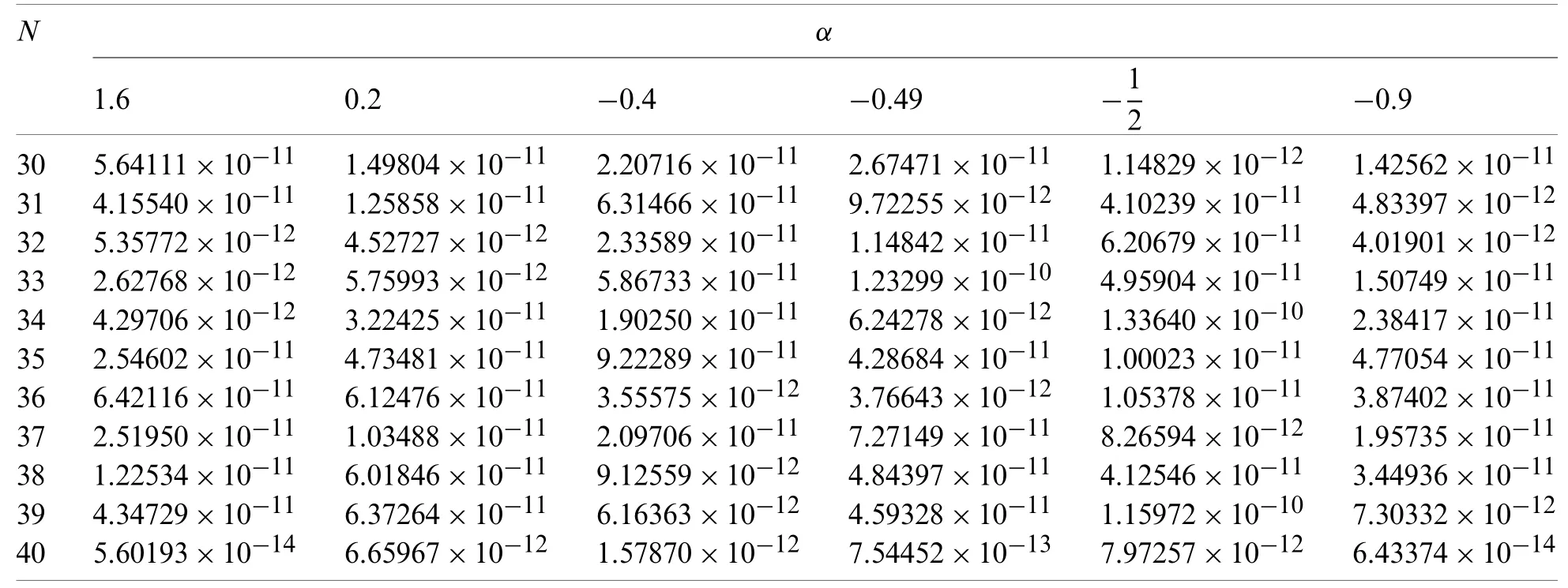
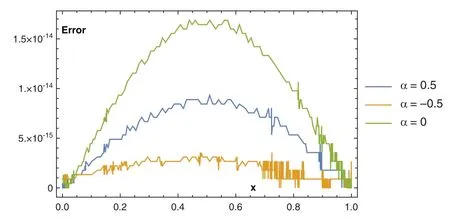
Theorem 7.1.If the exact solution in(92)isCq-function,for someq>3,|u(i)|≤Li,1 ≤i≤qand for 2α+4 (1)The expansion coefficientsansatisfy the following estimate:. (2)The series in(92)converges uniformly. Proof.Due to(8),the expansion coefficientsanare given by It is clear from relation(9)that,and consequently Thanks to the connection formula(83)that linkswith the shifted Legendre polynomials,we have and in virtue of Lemma 7.3,the last inequality gives Now,if we apply integration by partsq-times and along with the following result obtained by Leibniz’s Theorem the following estimate can be obtained Now,the direct application of Lemma 7.2,and after performing some manipulations,yield By the hypothesis of the theorem,precisely,the boundedness of the derivativesu(r),we get, which completes the proof of the first-part of the theorem. For the second part,we have and with the aid of the first result of this theorem along with Lemma 7.4,we get Taking into consideration the condition:q>2α+4,and applying the integral test,the desired series converges uniformly,and this completes the proof of the second-part of the theorem. Theorem 7.2.Under the hypotheses of Theorem 7.1,the following truncation error estimate is valid: Proof.Using relations(92)and(93),it is clear that Now,by the result of Theorem 7.1 along with Lemma 7.4 yield the following inequality: Now,based on the asymptotic behaviour of the Riemann–Hurwitz function,we have which completes the proof of the theorem. Remark 7.1.The main idea to investigate the convergence and error analysis of the expansion that used in Section 4 is built on transforming the basis functions(45)into another suitable form,and after that perform similar procedures to those followed in Subsections 7.1 and 7.2.More precisely,the following theorem is the key for such study.It can be proved through induction. Theorem 7.3.Letbe the basis functions in(45).The following identity holds for every positive integern In this section,we give some numerical results obtained by using our two proposed algorithms,namely,shifted Jacobi Galerkin method(SJGM)and the shifted Jacobi collocation method(SJCM)which presented,respectively,in Sections 4 and 5.Furthermore,some comparisons between our two proposed algorithms with some other methods exist in the literature are presented hoping to show the efficiency and accuracy of our proposed methods.In this section,the symbolNrefers to the number of retained modes.In addition,u(x)is the exact solution anduN(x)is the corresponding approximate solution and the error is denoted byEwhere. Example 1.Consider the sixth-order linear boundary value problem[46,47] subject to the boundary conditions The exact solution for this problem is:. Tab.1 lists the maximum absolute errorsEfor various choices ofN,c,andα.In Tabs.2 and 3,comparisons between our proposedSJGMand the two methods developed in[46,47]are displayed.In addition,in Fig.1,we depict the Log-error plot of Example 1 for the case corresponds to various values ofNandα. Table 1:Maximum absolute error of E for Example 1 Table 2:Errors at xi for N=12 and c=10 for Example 1 Table 3:Errors at xi for N=12 and c=1000 for Example 1 Figure 1:Log-error of Example 1 for c=1 Remark 8.1.The results in Tab.1 show that the case corresponding to third-kind Chebyshev polynomialsdoes not always give the best results. Example 2.Consider the eighth-order linear boundary value problem[48] subject to the boundary conditions The exact solution for this problem is:u(x)=(1 −x)ex. Tab.4 presents the maximum absolute errorEfor some choices ofαandN,while Tab.5 lists a comparison between our proposed algorithm with the absolute errors obtained by the method proposed in[48].In Fig.2,we depict the absolute error plot of Example 2 for the case corresponds toN=14 and various valuesα. Table 4:Maximum absolute error of E for Example 2 Table 5:Errors at xi for N=14 for Example 2 Figure 2:Absolute error plot of Example 2 Example 3.Consider the eighth-order nonlinear boundary value problem[49,50] subject to the boundary conditions The exact solution for this problem is:u(x)=ln(x+1). Tab.6 lists the maximum absolute errorEfor various values ofNandα.For the sake of comparison with other methods,we compare the best errors obtained from the application of our algorithm with those obtained by the two methods developed in[49,50].Tab.7 displays these results. Example 4.Consider the twelfth-order nonlinear boundary value problem[51,52] subject to the boundary conditions: The exact solution for this problem is:u(x)=2ex. Tab.8 presents the maximum absolute errorEfor some choices ofαandN,while Tab.9 lists a comparison between our proposed algorithm forN=21 for various values ofαwith the best errors obtained by the methods developed in[51,52].In Fig.3,we depict the absolute error plot of Example 4 for the case corresponds toN=21 and various valuesα. Table 6:Maximum absolute error of E for Example 3 Table 7:Best errors for N=40 for Example 3 Table 9:Best errors for Example 4 Figure 3:Absolute error plot of Example 4 Some direct algorithms for treating both linear and nonlinear BVPs were analyzed and presented.The proposed solutions are spectral.Two different approaches were presented for solving such problems.In the linear case,a Galerkin approach is followed.The basis functions are expressed in terms of certain Jacobi polynomials which generalize the well-known Chebyshev polynomials of the third- and fourth-kinds.Another collocation approach is followed for the treatment of both linear and nonlinear BVPs.A new operational matrix of derivatives of certain shifted Jacobi polynomials was constructed for this purpose.The presented numerical results show that the expansion of the third-kind of Chebyshev is not always the best in approximation.Moreover,the numerical results show that our algorithms are applicable and of high accuracy. Acknowledgement:The authors would like to thank the anonymous reviewers for carefully reading the article and also for their constructive and valuable comments which have improved the paper in its present form. Funding Statement:The authors received no specific funding for this study. Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.

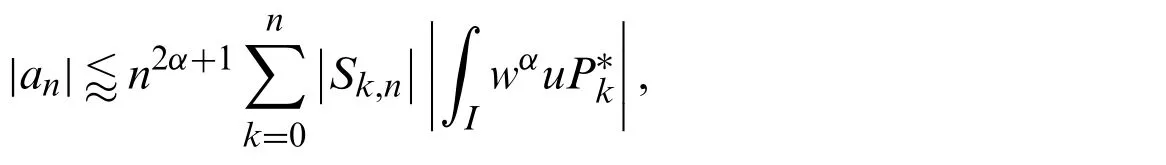







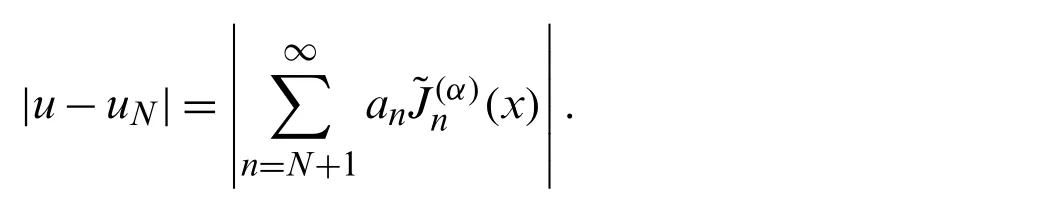
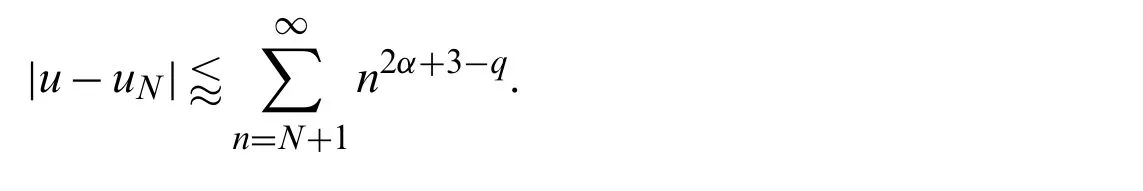

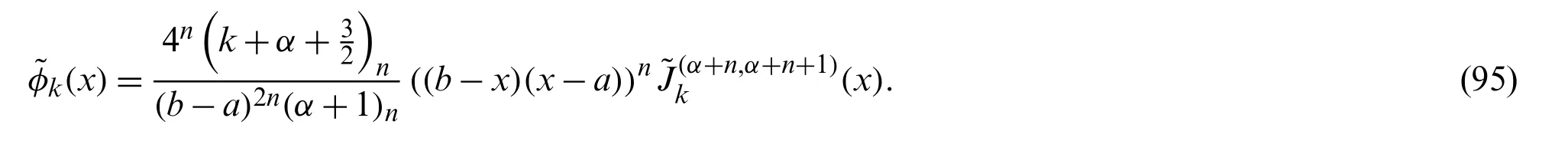
8 Numerical Results
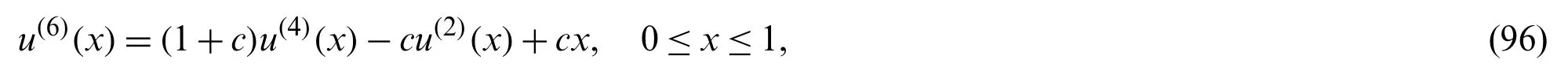
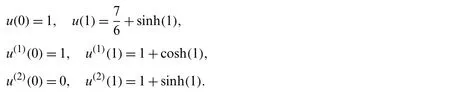



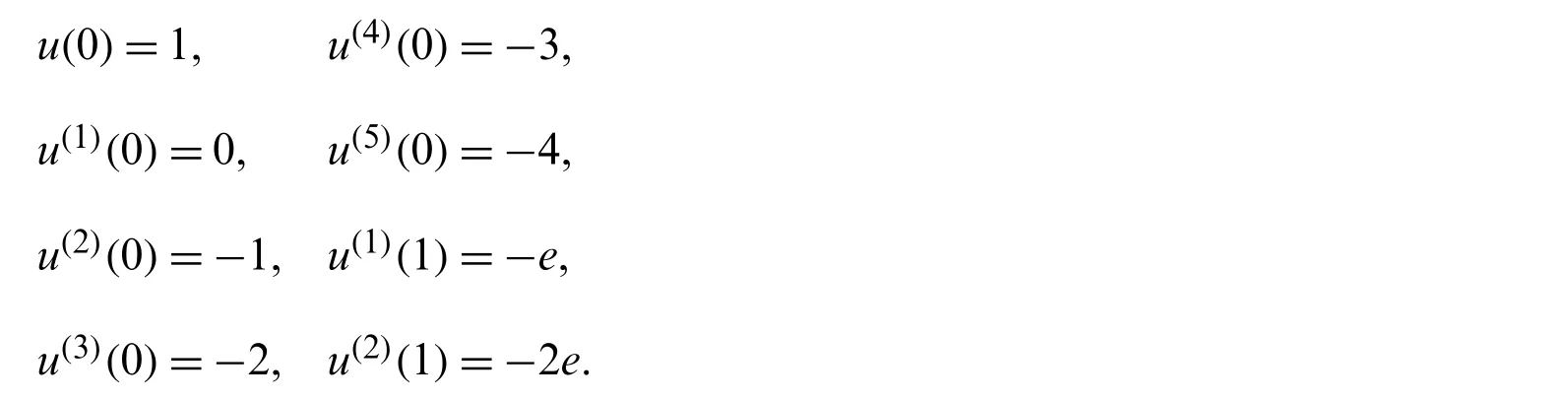


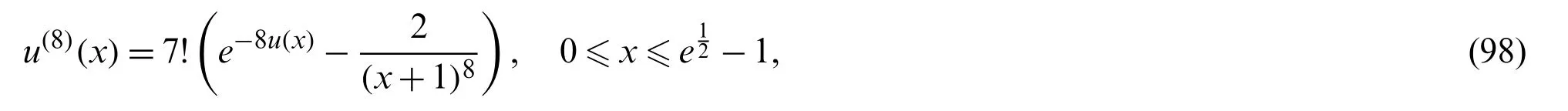





9 Conclusions
 Computer Modeling In Engineering&Sciences2021年3期
Computer Modeling In Engineering&Sciences2021年3期
- Computer Modeling In Engineering&Sciences的其它文章
- Simulating the Turbulent Hydrothermal Behavior of Oil/MWCNT Nanofluid in a Solar Channel Heat Exchanger Equipped with Vortex Generators
- Fabrication and Statics Performance of Pyramidal Lattice Stitched Foam Sandwich Composites
- A Smart Wearable Ring Device for Sensing Hand Tremor of Parkinson’s Patients
- Spherical Linear Diophantine Fuzzy Sets with Modeling Uncertainties in MCDM
- Adaptive Extended Isogeometric Analysis for Steady-State Heat Transfer in Heterogeneous Media
- Numerical Analysis of Labyrinth Seal Performance for the Impeller Backface Cavity of a Supercritical CO2 Radial Inflow Turbine
