转动圆柱对封闭腔内混合对流换热的影响研究

高 杰，郭小勇，宋克伟*

(1. 机电工程学院 铁道车辆热工教育部重点实验室，兰州 730070; 2. 泛仕达机电股份有限公司西安分公司，西安 528300)

受限空间内的对流换热问题可分为纯自然对流[1-6]、含内置物的自然对流[7-10]以及含转动内置物的混合对流[11-15].杨力等[1]对航空刹车机轮腔体内的自然对流进行了数值模拟，分析了中间环形狭缝内的流动换热规律，获得了航空器刹车轮腔体内关键部位的流动特征.匡东升等[2]研究了倾斜封闭腔内的自然对流，分析了倾斜角和Ra数对腔内自然对流换热的影响，获得了自然对流换热的腔体最佳倾斜角度和Ra数.任嘉友等[3]对不同Ra数及高深宽比下的方腔内空气自然对流换热进行了研究，发现随着Ra数增大，Nu数增大，而且温度场与速度场在几何上具有良好的中心对称特性.宋克伟等[4-6]数值研究了梯度磁场对自然对流的抑制作用以及磁场强度变化对方腔内流场和温度场的影响，发现随着磁场强度增大，方腔内自然对流逐渐减弱.陈中豪等[7]采用数值模拟的方法分析了内置圆形发热体位置对二维方腔内自然对流的影响，得到了不同情况下的Nu数变化范围及趋势.Park等[9]对内有圆柱的倾斜方腔内的自然对流进行了数值分析，发现温度场、流场分布与壁面Nu数是由自然对流作用以及圆柱体距方腔壁面距离的组合效应决定的.Kim等[10]对冷外方管和热内圆管温差引起的自然对流进行了数值计算，发现随着内圆柱竖直位置和Ra数的变化，内圆柱上表面附近的涡对局部和平均Nu数的分布有很大影响.

针对封闭腔内含有转动内置物的问题也正被广泛关注.方腔内带有转动件的换热问题属于混合对流换热，既需要考虑转动件引起的强制对流，也需要考虑温差引起的自然对流.Barnoon等[11]数值分析了方腔倾角、圆柱转速、热边界条件以及磁场强度对方腔内纳米流体在磁场中流动与换热的影响，腔内设置圆柱及圆柱转动速度可以改善腔内对流换热，并且等温圆柱更有利于增强换热.Khanafer等[12]对带转动圆柱的顶盖驱动腔体的混合对流换热进行了数值分析.结果表明：平均Nu数与角速度的方向有关，对于不同的理查森数Ri，平均Nu数随圆柱顺时针角速度的增加而增加；随圆柱逆时针方向角速度的增加而减小，直到达到一个临界角速度后又随着角速度的增加而增加.Selimefendigil等[13]数值分析了转动圆柱转速、转向、大小和位置对方腔内相变材料融化过程的影响，发现腔内相变材料传热及融化过程可以通过圆柱转动速度进行调节.Alam等[14]研究了含导热转动圆柱的方腔内混合对流换热现象，对不同转速下的定常层流混合对流问题进行了分析.结果表明：流场、温度分布和传热速率与转速和圆柱尺寸有关.Khanafer等[15]分析了两个转动圆柱位置、转向和速度对腔内混合对流的影响，发现理查森数为10时，转速对换热的影响很小.

封闭腔内转动部件的转动方向，可以导致腔内自然对流换热的增强或减弱.现有关于内置转动圆柱方腔内混合对流换热的研究相对较少且内置圆柱多为导热圆柱，而关于绝热旋转圆柱的研究未见报道.基于此，本文在不同Ri数、Ra数和Re数下,数值分析了绝热圆柱转动方向对腔内流场、温度场及换热的影响，并与圆柱不转动时进行了对比.

1 物理模型和计算方法

1.1 混合对流物理模型

二维封闭方腔内含有一绝热转动圆柱的物理模型如图1所示.腔体边长为L×L，圆柱直径D=0.2L=1 cm.方腔顶面、底面和圆柱表面绝热，左侧壁面温度为Tc；右侧壁面温度为Th，且Th>Tc.腔体内介质为空气，Pr=0.701，重力加速度方向为y轴负方向.定性温度取0.5(Th+Tc)=303.15 K，所有物性参数均取定性温度下的数值.

1.2 控制方程及数值方法

二维封闭方腔内对流传热控制方程为：

(1)

(2)

(3)

(4)

其中:ρ为空气密度，u和v为x和y方向速度，μ为动力粘性系数，cp为比热容，k为导热系数.

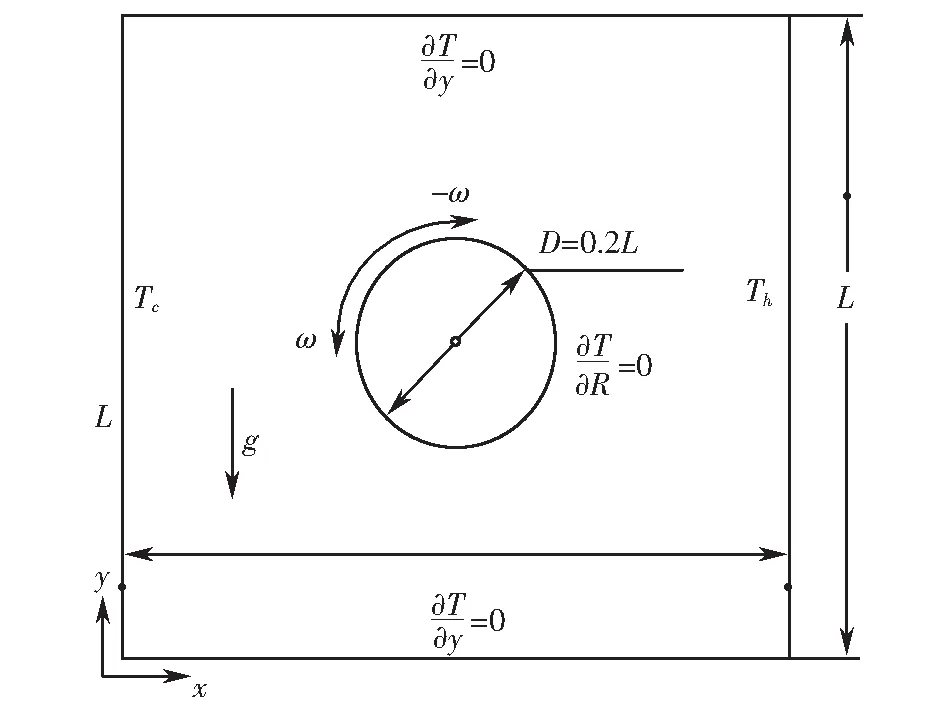
图1 模型示意图 Fig1 Model diagram

本文模型比单纯的自然对流或强制对流更为复杂，属于浮升力和惯性力共同作用的混合对流问题.在自然对流中，Gr数表示作用在流体上的浮升力与粘滞力的相对大小.在强制对流中，Re数表示流体惯性力与粘滞力的相对大小.在混合热对流问题中，用Ri数表示相对于强制对流的自然对流所占比重大小.各无量纲数定义为：

(5)

其中：g为重力加速度，β为热膨胀系数，L为特征长度，ν为流体运动粘度，α为热扩散系数，ω为圆柱转动角速度.

热壁面局部努塞尔数Nulocal和平均努塞尔数Nuave：

(6)

数学模型边界条件：

x=0,u=v=0,T=Tc;x=L,u=v=0,T=Th;y=0,u=v=0,∂T/∂y=0;y=L,u=v=0,∂T/∂y=0.

转动圆柱表面：∂T/∂R=0.

采用有限体积法进行离散求解，采用SIMPLE算法，动量和能量方程均采用二阶迎风格式进行离散.空气密度采用Boussinesq近似，忽略耗散项和高温壁面的辐射作用，并假定所有的物性参数均为常数.数值计算中各个物理变量残差的收敛标准取为10-12.

选取四套网格8 204,12 734,24 600和32 656进行数值结果的网格独立性考核.Re=150，Ri=0.1时，四套网格所得热壁面平均努塞尔数Nuave分别为2.978 7,2.977 9,2.977 4,2.977 6，最大误差为0.043 6%，因此结果具有网格独立性，计算选取网格数12 734的网格.

表1 本文与文献中模型数据对比

为了验证数值计算方法和结果的正确性，针对封闭方腔内的混合对流换热问题，Ra=105时数值结果与Park[9]、Kim[10]及Alam[14]中的结果进行了对比，如表1，边界条件的设定与文献中保持一致.Ra=104～106范围内，数值结果与文献结果具有一致性.图2为数值方法得到的与Kim[10]中相同方腔模型内的等温线与流线的对比，方腔内的等温线及流线十分吻合，验证了本文数值方法的准确性.

2 结果分析与讨论

首先固定Re=150，分析了圆柱转动方向对不同Ri数下(Ri=0.1，Gr=2.25×103；Ri=1.0，Gr=2.25×104；Ri=10，Gr=2.25×105)方腔内混合对流的影响.其次固定Gr=5×104，分析了不同Ri数(Ri=0.1，Re=707.11;Ri=1，Re=223.61;Ri=10，Re=70.71)下，圆柱转动方向对方腔内混合对流的影响.最后，对比分析了不同Ri数和转动方向时热壁面局部Nu数和平均Nu数分布.

图2 等温线及流线与Kim[10]中结果对比Fig.2 Comparison of the isotherm and streamlines between the present work and that of Kim[10]

2.1 Re=150，不同圆柱转动方向和Ri数下流动及温度场分析

图3为Re=150，圆柱逆时针(图3(I))和顺时针(图3(II))转动时，方腔内的流线及流场.图3(I-a)和(II-a)分别为不考虑自然对流，仅圆柱逆时针/顺时针转动时方腔内的流线及流场，图3(b)-(d)为Ri分别取0.1，1.0及10，圆柱逆/顺时针转动时方腔内的流线及流场.Ri=0.1时，浮力效应很小，自然对流作用可忽略不计，圆柱周围的流体在粘滞力作用下随圆柱转动，并且在方腔四个拐角处各存在一个小涡，如图3(b)所示，这与图3(a)中纯圆柱转动而不考虑自然对流时的情况是一致的.Ri数增大到1时，此时强制对流与自然对流共同作用于流体；圆柱逆时针转动时，强制对流与自然对流的作用一致，与图3(I-b)相比，方腔拐角处的小涡消失，流体绕圆柱逆时针流动，如图3(I-c)；圆柱顺时针转动时，自然对流引起的逆时针方向的流动和圆柱转动引起的顺时针方向的流动相反，在混合对流作用下，圆柱顺时针转动引起的强制对流被自然对流消弱，拐角处涡的大小明显比Ri=0.1时增大，如图3(II-c).Ri数增大到10时，浮力效应大于转动圆柱的效应，自然对流开始占据主导地位；圆柱逆时针转动时，方腔内部因自然对流和圆柱转动形成的逆时针涡完全占据方腔，如图3(I-d)；而当圆柱顺时针转动时，圆柱转动和自然对流引起的流体流动方向相反，自然对流的作用大幅度超越了圆柱转动的作用，因而在圆柱左右两侧形成一对呈中心对称的涡，如图3(II-d).

图3 流线及流场Fig.3 Streamlines and velocity fields

图4 方腔内温度云图Fig.4 Temperature field

Re=150,不同圆柱转动方向下，方腔内温度云图如图4所示.图4(I-a)和(II-a)分别为圆柱逆时针/顺时针转动且不考虑自然对流时方腔内的温度场，图4(b)-(d)为Ri分别取0.1，1.0及10时的混合对流温度场.Ri=0.1时，热壁处等温线近似平行，壁面热量传递主要以导热方式进行；同时，由于圆柱体的转动，温度场在圆柱体外围被诱导出了一个对流峰，其转向由圆柱体转动方向决定.随着Ri数增大，方腔内的流动逐渐由强制对流为主导的换热向自然对流为主导的换热过渡.Ri=1时，自然对流作用逐渐增强，热壁面上方温度增大，梯度减小；而Ri数增大到10时，方腔内自然对流已占主导地位.圆柱逆时针转动时，热壁面附近温度从下部向上部逐渐增大，温度梯度逐渐减小，而冷壁面附近变化相反；在自然对流和强制对流的共同作用下，流体逆时针转动，对流峰强度变大，如图4(I-d).圆柱顺时针转动时，由于自然对流占主导地位且自然对流引起的流动与圆柱转动引起的流动方向相反，圆柱转动引起的流动被消弱，对流峰减弱，温度分布与Ri=1时完全不同，如图4(II-d).

2.2 Gr=5×104，不同Ri数和圆柱转动方向下方腔内流动和温度场分析

Gr=5×104，变化Re数使得Ri数分别为0.1，1和10时，圆柱转动方向对方腔内混合对流的影响如图5(II-III)所示.图5(I)为圆柱转速为零时方腔内自然对流流线图.在纯自然对流情况下，流体逆时针流动，在圆柱体两侧形成两个对称涡.圆柱逆时针转动时，圆柱转动引起的流动和自然对流引起的流动方向一致，在方腔内形成一个逆时针的大涡；在Ri=0.1时，自然对流的作用较小，方腔内以强制对流为主，在方腔的四角各诱导出一个小涡，如图5(II-a)所示；随着Ri数的增加，自然对流逐渐增强，方腔内4个角的小涡逐渐消失；在Ri=10时，图5(II-c)与图5(I)相比，除圆柱周围没有小涡外，方腔内流线呈现出与纯自然对流相似的特性.圆柱顺时针转动时，如图5(III)，圆柱转动引起的流动方向与自然对流引起的流动方向相反；在Ri=0.1时，自然对流引起的流动较弱，方腔内流体在转动圆柱的驱动下，在方腔内形成一个顺时针转动的大涡，同时在方腔的四个角各形成一个逆时针转动的小涡；随着Ri增大，自然对流逐渐增强，圆柱转动引起的顺时针转动的涡逐渐减弱，在自然对流的作用下方腔四个角的小涡逐渐增强；在Ri=10时，方腔内混合对流以自然对流为主导，自然对流驱动流体逆时针流动，而圆柱转动引起的顺时针流动的流体区域减小，方腔四角的涡随着圆柱引起的顺时针流动区域的减小和自然对流引起的逆时针流动区域的增大，逐渐向圆柱四周靠近，如图5(III-c)所示.

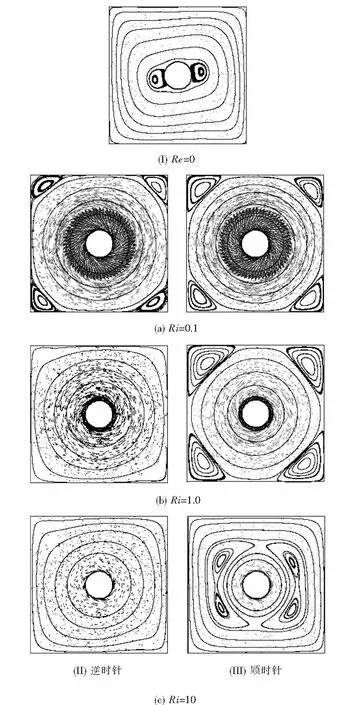
图5 流线及速度矢量图Fig.5 Streamlines and velocity field

图6为与图5对应的温度场.腔内为纯自然对流时，在浮升力的作用下，热壁面处温度随着流体向上流动逐渐增大.在圆柱转动时，由于Gr数固定，随着Ri数增大，Re数逐渐减小，方腔内流动由强制对流占主导向自然对流占主导过渡.圆柱逆时针转动时，圆柱转动对自然对流的促进作用随着Ri数的增大逐渐减弱，在圆柱转动的促进下，壁面温度梯度明显大于图6(I).在Ri=10时，如图6(II-c)所示，方腔内的温度场除圆柱周围外，其它区域与纯自然对流温度场相似.圆柱顺时针转动时，在Ri=0.1时，方腔内流体在转动圆柱的驱动下顺时针转动，流体沿着热壁面向下温度逐渐增高.随着Ri数增大，圆柱转动速度减小，圆柱诱导的对流峰的强度不断减弱.热壁面附近流动速度先由于流体向下流动逐渐减小，Ri数增大到一定值后，流体在浮升力驱动下沿着热壁面开始向上流动又逐渐增大.在Ri=10时，除圆柱周围外，方腔内流体逆时针流动，热壁面温度从下往上逐渐增大，由于圆柱顺时针转动消弱了自然对流，图6(III-c)中热壁面温度梯度明显要小于图6(II-c).与图6(I)中圆柱无转动的纯自然对流情况相比较，图6(II)中圆柱逆时针转动对自然对流有明显的促进作用，而图6(III)中圆柱顺时针转动则对自然对流有着明显的抑制作用.

图6 方腔内温度云图Fig.6 Temperature field

2.3 不同圆柱转动方向和Ri数下热壁表面换热Nu数分析

圆柱逆时针和顺时针转动时，不同Ri数下方腔热壁面Nulocal分布如图7所示.图7(a)为Re=150，Ri=0.1，1和10三种情况下，方腔内热壁面局部Nulocal对比.圆柱逆时针转动时，由于圆柱转动引起的流动和自然对流流动一致，Nu数随着Ri数的增大而增大.在Ri=0.1和1时，热壁面Nulocal在逆时针转动圆柱引起的流动影响下，Nulocal峰值靠近壁面0.4位置处，在热壁面上端处最小.在Ri=10时，自然对流占主导地位，Nulocal最大值在热壁下端温度梯度最大的位置.圆柱顺时针转动时，圆柱引起的顺时针流动起到消弱自然对流逆时针流动的作用，热壁面Nulocal分布与圆柱逆时针转动时明显不同.圆柱顺时针转动时，随着Ri数由0.1增大为1，Nulocal减小.这是因为在Ri数由0.1增大到1时，虽然自然对流逐渐增强，但圆柱转动引起的强制对流被消弱，使得方腔内总的对流强度减弱.在Ri=0.1和1时，Nulocal峰值靠近壁面0.6位置处.随着Ri数由1继续增大到10时，自然对流逐渐占主导地位，Nulocal随着自然对流的增强而增大，Nulocal最大值在热壁面靠近底部温度梯度最大的位置.Ri=10时，壁面下部Nulocal大于Ri=1时的值，而热壁面上部由于自然对流引起的流体温度增大、温度梯度减小，使得Nulocal继续减小并小于Ri=1时的值.当Ri=0.1及Ri=1时，圆柱逆时针转动时的Nulocal峰值高于顺时针转动，且最大相差分别为1.89%和19.33%；当Ri=10，在自然对流影响下，圆柱逆时针转动时的Nulocal峰值比顺时针转动时小19.16%.

图7 不同Ri数下热壁面Nulocal数分布Fig.7 Distribution of Nulocal along the hot wall for different Ri

图7(b)为Gr=5×104，Ri=0.1，1和10三种情况下，不同圆柱转动方向方腔内热壁面Nulocal对比.圆柱逆时针转动时，热壁面Nulocal基本随着Ri数的增大而减小，这与图7(a)中的规律相反.这是因为随着Ri数的增大，圆柱转速减小，圆柱逆时针转动时引起的流动对自然对流的促进作用减小，从而Nulocal减小.但在热壁面底部靠近底角处，由于Ri数增大，圆柱逆时针转动引起的流动逐渐减弱，方腔四角处的小涡逐渐减小，自然对流使得热壁面底部温度梯度增大.因此，热壁面Nulocal随着Ri数的增大而增大.在Ri=0.1和1时，热壁面Nulocal峰值靠近壁面0.4位置处.圆柱顺时针转动时，随着Ri数的增大，圆柱转速减小，方腔内混合对流由强制对流主导逐渐过渡到自然对流主导.Ri数从0.1增大到1时，Re数减小，Nulocal也逐渐减小，热壁面Nulocal最大值在0.6附近.Ri=10时，方腔内混合对流以自然对流占主导地位，在自然对流引起的流动影响下，热壁面Nulocal增大，而热壁面上部Nulocal继续减小，Nulocal最大值在热壁面底部温度梯度最大处.当Ri=0.1及Ri=1时，圆柱逆时针转动时的Nulocal峰值也依然高于顺时针转动时的值，且最大相差分别为3.96%和26.17%.当Ri=10时，圆柱逆时针转动时的Nulocal峰值比顺时针转动时小11.54%.

分别固定Re数和Gr数，在不同圆柱转动方向下，方腔内Nuave随Ri数的变化如图8所示.在固定Re=150，圆柱逆时针转动时，Nuave随Ri数增大而增大.这是因为Re数不变时，Gr数随Ri数的增大而增大，自然对流换热增强，圆柱逆时针转动引起的流动对自然对流起促进作用，因而方腔内混合对流随Ri数增大而增强.而在固定Gr=5×104，圆柱逆时针转动时，Nuave随Ri数增大而减小，这与固定Re数圆柱逆时针转动时的变化规律相反.这是因为固定Gr数时，壁面温差保持不变，随Ri数增大Re数减小，圆柱转动速度的减小，使得与自然对流流动方向一致的圆柱引起的流动减弱，从而混合对流减弱，腔体内换热性能下降.圆柱顺时针转动，固定Re数或Gr数时，Nuave随Ri数的变化规律一致，都是随着Ri数的增大先减小后增大，在Ri=2时都具有最小值.这是因为Ri数增大，自然对流强度逐渐增强或者强制对流作用逐渐减弱.在Ri=0.1时方腔内圆柱引起的强制对流占主导地位.固定Re数，Gr数随着Ri数的增大而增大，自然对流逐渐增强，逐渐消弱了圆柱引起的顺时针流动，使得方腔内的混合对流减弱；固定Gr数，Re数随着Ri数增大而减小，强制对流逐渐减弱，导致方腔内对流整体减弱.在Ri>2时，方腔内的自然对流已占主导地位，混合对流的强度随着Ri数的增大而增大.在Ri数足够大时，方腔内自然对流占主导地位，圆柱转动以及转动方向对方腔内混合对流的影响很小，因此Ri>50时圆柱逆时针或顺时针转动时Nuave基本相同.

图8 不同圆柱转动方向时,Nuave随Ri变化规律Fig.8 Distribution of Nuave as a function of Ri for different rotating directions

由于圆柱逆时针转动引起的流动与自然对流流动方向一致，而圆柱顺时针转动引起的流动与自然对流流动方向相反，在Ri数较小时，圆柱逆时针转动时的Nuave比圆柱顺时针转动时大，且差值在Ri<2时随着Ri数的增大而增大.当Ri=2时，圆柱不同转动方向对Nuave的影响最大，对于固定Re数和Gr数两种情况，圆柱逆时针转动时Nuave分别比顺时针转动时提高约91.9%和93.6%.在Ri>2时，圆柱转动方向引起的Nuave的差别逐渐减小.固定Gr数不变时，圆柱不同转动方向对应的Nuave在Ri>50时相差很小，数值基本相同.固定Re数且在750时，两者相差很小，Nuave基本相同.Ri<2时，在相同圆柱转动方向下，固定Gr数时要比固定Re数时的Nuave大，而Ri>2时情况相反.因此，在Ri<2时，改变Re数可以获得更好的混合对流换热效果，而在Ri>2时改变Gr数则可以获得更好的混合对流换热性能.

3 结论

数值分析了含有转动圆柱方腔内的空气混合对流换热，对比了圆柱转动方向对混合对流换热的影响，主要结论总结如下：

1)Ri数由0.1变化到10时，混合流动由强制对流占主导逐渐向自然对流占主导过渡.在Ri数不大时，圆柱转动方向对方腔内流场和温度场影响显著，而当Ri数较大时，圆柱转动对流场的影响主要在圆柱周围，而方腔四周流场主要受自然对流控制.

2) 圆柱转动引起的流动与自然对流引起的流动方向一致时，固定Re数使Ri数在0.1～100间变化时，方腔内Nuave随着Ri数的增大而增大；而固定Gr数时，Nuave随着Ri数的增大而逐渐减小.

3) 圆柱转动引起的流动与自然对流引起的流动方向相反时，方腔内Nuave随着Ri数的增大先减小再增大；在Ri=2时，Nuave具有最小值且圆柱不同转动方向对方腔内Nuave的影响最大；对于固定Re数和Gr数两种情况下，圆柱转动与自然对流流动方向一致时的Nuave分别比流动方向相反时提高约91.9%和93.6%.

4) 在Ri<2时，改变Re数可以获得更好的混合对流换热效果，而在Ri>2时改变Gr数则可以获得更好的混合对流换热效果.