软土地铁车站抗浮梁抗震性能有限元分析

轩俊杰，严松宏*,2

(1. 兰州交通大学 土木工程学院，兰州 730070；2. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，兰州 730070)

随着近些年我国轨道交通工程基建规模的增大，一大部分在建的地铁车站出现了覆土埋深较浅、地下水位较高、地下结构受浮变位的现象，这使得地铁车站的抗浮设计越来越受到人们的重视.加之位于饱和软土地基中的地下结构，由于软土地基会显著放大地震动载作用，从而导致结构破坏程度的加剧.虽然目前国内很多学者已对地下结构的抗震稳定性做了大量研究，但软弱土层中地下结构抗震的理论分析与模拟计算、施工工程中设置抗浮梁是否有效等仍是亟待解决的问题.

地震工程学专家胡聿贤[1]提出，地铁车站结构抗震设计方面的难点在于结构在受到地震动载作用时，除了要具备足够的刚度、强度以抵抗地震动载作用，还应具有一定的柔度以充分吸收结构周围岩土体的变形，从而减小结构在地震中受到的破坏；刘晶波等[2]阐述了几个需要尽快解决的关键问题：如何建立科学的结构-土体动力相互作用分析方法，如何建立相符的地下结构动力分析模型，如何提出适用的地下结构抗震构造措施等；周林聪[3]通过对地铁车站的框架结构进行了数值动态模拟的研究，得出了关于地震响应的一般规律，然并未充分考虑结构与土体之间发生的流塑变形；严松宏[4]借助地下结构抗震和结构动力分析的脉冲响应函数原理，提出了地下结构地震动力响应计算的加速度脉冲函数法；欧尔峰等[5]基于杜修力地震模型，对某隧道进行了随机动力响应分析，通过求解嵌套脉冲函数的动力方程，研究了随机地震动荷载作用下该隧道的地震响应特征；杨林德等[6]利用振动台试验对地铁车站结构模型进行了数值分析，得到了车站在地震动载作用下的响应及土体-结构相互作用规律；邓爽[7]利用有限元分析软件基于某区间隧道相关数据，建立了地铁车站结构的三维有限元实体模型，对多种工况下的围岩-衬砌结构进行了地震响应分析.

本文研究的天津地铁5号线某车站所在地层的土质属软土类，地震发生时会加大地震危害程度，因此有必要结合围岩岩性条件和地下工程本身的结构特点，对天津地区软土地层当中的地铁车站结构进行理论研究与设计理念的深层次探索.本文研究主要针对于车站地下连续墙上设置的抗浮压顶梁是否会脱离车站主体结构，并对其进行数值模拟分析，研究抗浮梁与主体结构在地震作用下的最大位移差是否超出抗浮梁的横向挑出长度，进而确定是否采取限位措施，以确保运营阶段的安全性与可靠性.

1 工程概况

天津地铁5号线主要沿中环的东南半环分布，全线地形相对平坦，岩性多变，地下水位较高，地下构筑物位于地表以下25～30 m内，部分粉砂层为轻微液化土层.区域场地土体基本是由饱和软土组成，地铁车站的上覆土层厚度约为2.2～6 m，车站结构的横断面宽度约18.73～33.45 m；地铁5号线车站的施工方法主要为明挖法，沿线场地岩土体主要以粉细砂、粉粘土为主，围岩等级为Ⅴ级，工程上为Ⅱ类场地；地铁车站在抗浮设计方面的措施主要为在地下连续墙顶部设置一道抗浮梁和在基底处设置若干锚索抗拔桩[8].在车站顶板上方，沿围护结构设置一圈矩形压顶梁，其截面尺寸为800 mm×800 mm.本地铁车站的结构框架图如图1所示.

图1 结构框架剖面图(单位：mm)Fig.1 Structural frame profile view(unit:mm)

该地铁车站的结构断面基本参数为：基坑宽度：20.7 m；基坑深度：17.15 m；覆土厚度：3.5 m；地下连续墙长度：32 m；土层计算范围：车站两侧不小于3B(B为车站跨度)，垂向不小于60 m.

2 计算模型及参数

车站结构与周围土体是一个相互影响、协同工作的整体，在二者相互作用中表现出明显的非线性特性[9].而相互作用问题存在两种非线性问题：一种是由于不连续、非均质、各向异性的岩土体所引起的材料非线性，本文拟选取Drucker-Prager本构模型来模拟围岩的材料非线性[10]；另外一种是由于地铁车站结构与围岩体之间发生相对位移而导致的状态非线性，本文拟通过采用接触单元来模拟土体-结构之间共同作用的接触非线性[11].常见的数值分析方法有两种，一种是基于有限元模型的数值分析方法；另一种是基于温克勒地基梁的简化方法[12].本文采用前者的方法.

2.1 计算模型建立

采用Midas GTS有限元计算软件，按平面应变问题进行分析.地层、地下连续墙及抗浮梁采用平面应变单元，主体结构(板、墙、柱)则采用梁单元来模拟，有限元模型取X方向(横向)140 m、Y方向(竖向)60 m (3倍车站跨度)，地应力场按自重应力场考虑.

建模结果中的模型正视图、车站主体结构图分别如图2～3所示.

图2 模型正视图Fig.2 Front view of the model

图3 车站主体结构图Fig.3 Main structure of the subway station

2.2 计算参数

模型材料参数如表1所列.

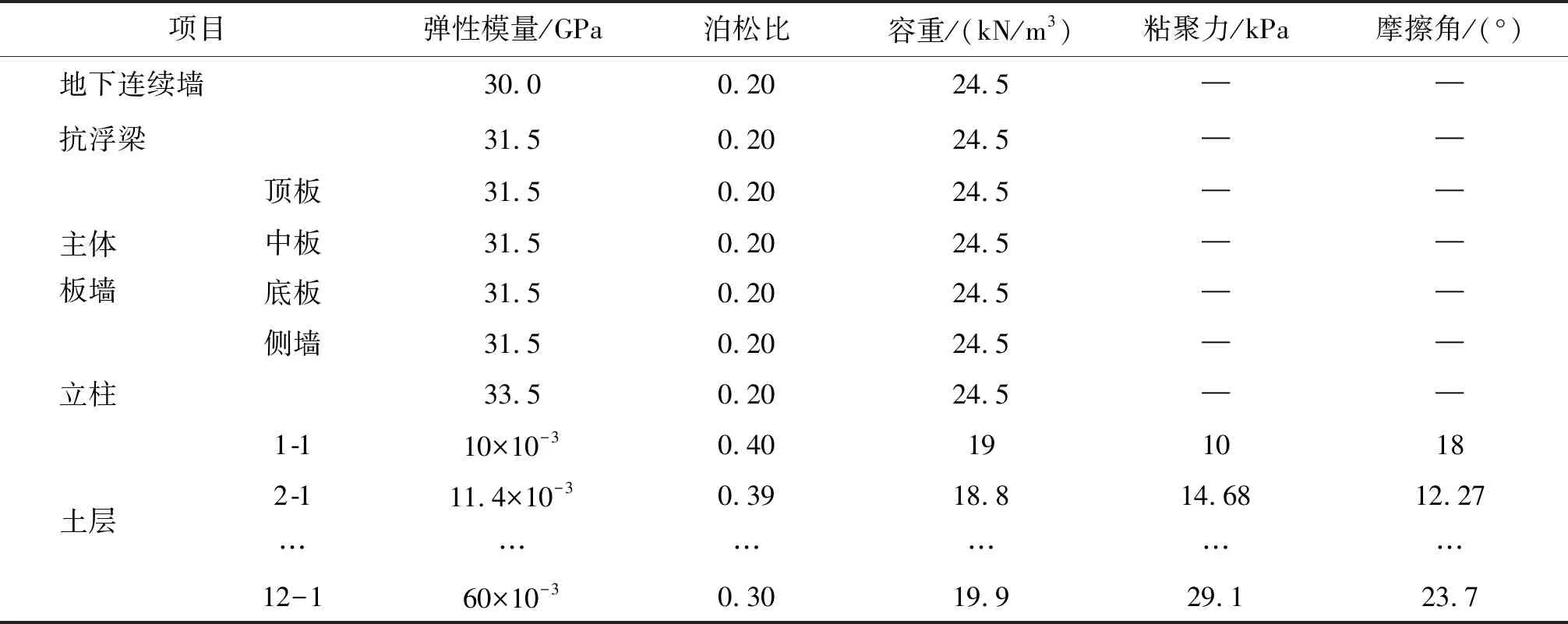
表1 材料及土层物理力学基本参数表

地基反力系数为：水平向：坑底以上取10 MPa/m；坑底以下取20 MPa/m；垂直向：30 MPa/m.各土层固有的阻尼系数根据土性参数计算出均值为Cp=288.43 kN·Sec/m3，Cs=145.36 kN·Sec/m3,各土层的阻尼系数计算表如表2所列.

2.3 边界条件及地面荷载

模型四周为法向约束，顶面取至地表为自由面，底面为垂向约束，两侧采用粘性边界条件；地下连续墙与主体受力结构、混凝土结构与周围岩土之间的界面，均采用虚拟接触单元，接触面只能受压，具有拉力截断的特性[13],以此来模拟结构与结构间、结构与岩土间不协调变形甚至错动开裂的特性，如图4所示.地面超载取为20 kPa.

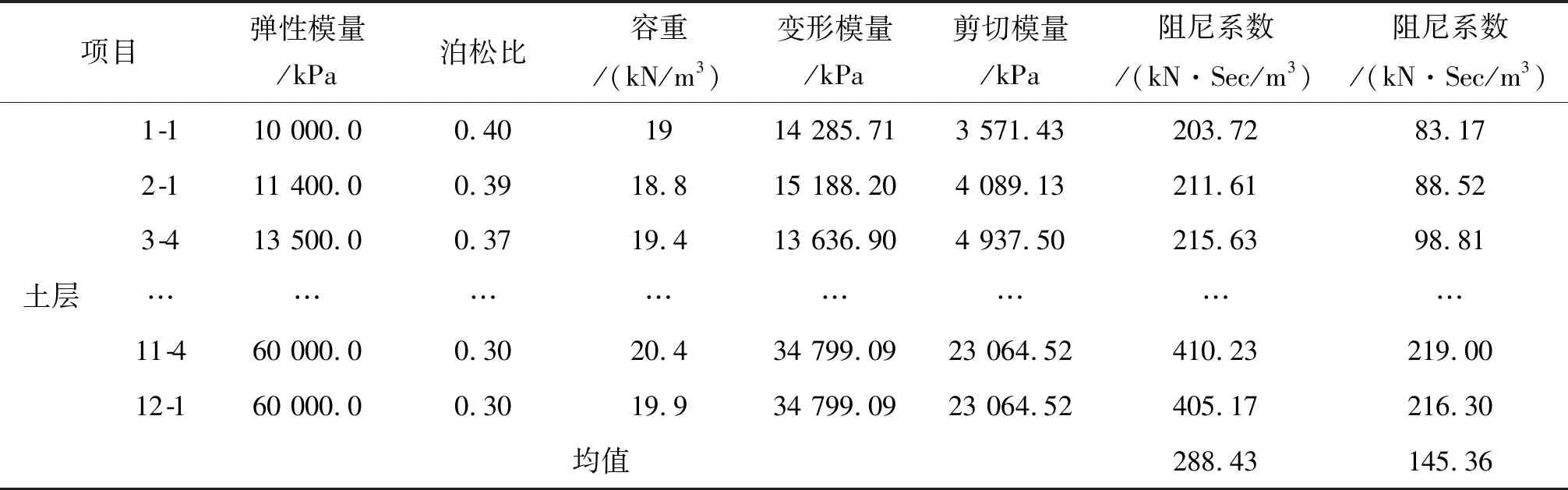
表2 各土层阻尼系数计算表

图4 接触单元示意图Fig.4 Contact unit diagram

2.4 地震波的选取

地铁5号线车站的场区基本烈度为7度，地震动峰值加速度取0.15g.根据地震烈度法，选取地震烈度方法-等级-类型III标准地震波[14]，峰值取0.143 1g，持续时间为49.96 Sec.地震波如图5所示.

3 数值分析结果

3.1 特征值分析结果

经分析计算获得模型特征值如表3所列.

3.2 地震作用动力分析结果

3.2.1 整体变形及位移

经计算，在地震作用下地层、结构、地下连续墙发生的最大正负位移图如图6～11所示，图中结构变形显示的是放大100倍后的效果.

图5 地震烈度方法-等级-类型III标准地震波Fig.5 Seismic intensity method-level-type III standard seismic waves

另外分别计算车站结构在时程为1 s、10 s、20 s、30 s、40 s、50 s的不同时刻下地下连续墙-结构发生震动的情况，以便分析其在震载作用下土层及结构随时间变化的位移规律，如表4所列.

由上表数据可以看出，地震作用情况下结构的位移还是以整体位移为主，地层、结构、地下连续墙、抗浮梁的最大正位移在85.55～87.75 mm之间，最大负位移在-103.43～-100.62 mm之间.在地质分层明显的土体中，由于土体弹性抗力系数的不同，对受力结构的约束作用大小也不尽相同，结构除发生上述的整体位移之外，还发生了一定的不均匀变形，这些不均匀变形将导致结构发生一定的扭转，从而在结构的内部产生剪扭作用.

表3 模型特征值

图6 地层最大正位移包络图Fig.6 Maximum positive displacement envelop graph of the stratum

图7 地层最大负位移包络图Fig.7 Maximum negative displacement envelop graph of the stratum

3.2.2 结构变形分析

在车站结构相应的分析位置上结构所发生的位移如图12所示，从图中可以看出在结构的顶板处位移最大，最大值为0.086 3 m；底板处较小，为0.077 1 m.如图13所示为顶板及底板角点水平位移曲线，最大负位移值为-0.093 m.

另外计算表明，地下车站结构顶板与底板在震动作用下发生的水平位移值，顶板处最大值为86.4 mm，最小值为-90.3 mm；底板处最大值为77.2 mm，最小值为-85.4 mm.

图8 结构最大正位移包络图Fig.8 Maximum positive displacement envelop graph of the structure

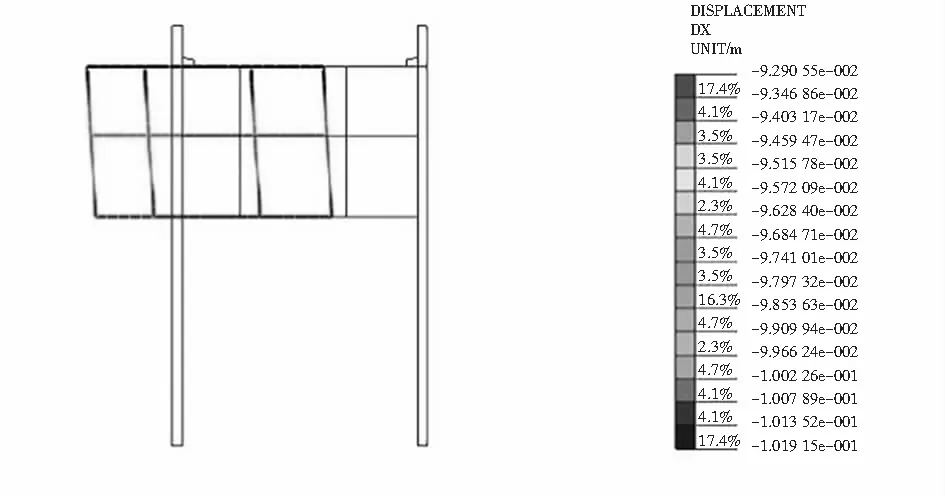
图9 结构最大负位移包络图Fig.9 Maximum negative displacement envelop graph of the structure

图10 地下连续墙最大正位移包络图Fig.10 Maximum positive displacement envelop graph of the underground diaphragm wall

图11 地下连续墙最大负位移包络图Fig.11 Maximum negative displacement envelop graph of the underground diaphragm wall

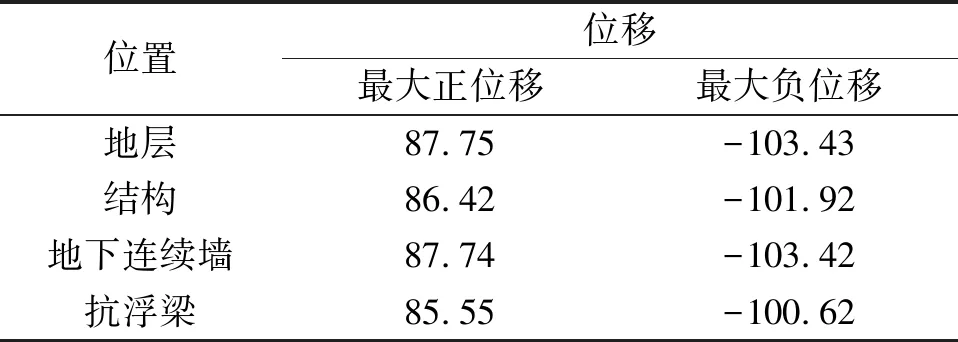
表4 位移统计表

图12 分析位置位移示意图Fig.12 Displacement schematic diagram of position to be analyzed

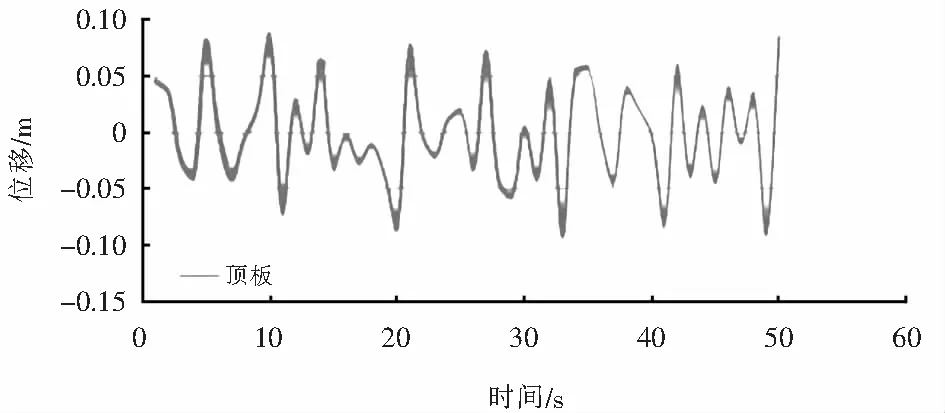
图13 顶板及底板角点水平位移曲线Fig.13 Horizontal displacement curve of the top and bottom plate

3.2.3 Y轴方向水平位移分析

由于地震时浅埋结构横截面沿高度方向各点地层位移是不同的，假设以结构底板为位移零点，则结构各点处所受到的强迫位移可假定呈余弦变化.

如图14所示模型计算结果与理论结果拟合程度较好，拟合出天津市基岩埋置深度约为62 m.因天津地铁5号线场区的地层在垂直方向上的分布情况是上部以粉质粘土为主，下部含大量的粉土、粉砂、细砂层，故地面震动位移较深层土体明显要大.

3.2.4 抗浮梁与地下连续墙、顶板之间的相对位移分析

如图15所示为抗浮梁与地下连续墙连接构造角点处发生的最大正位移包络图，可以看出其最大位移值为86.3 mm.

在构造措施上，应满足以下要求：对于地下连续墙的复合型墙体，其楼板和梁体中均应设置负弯矩钢筋，且应有不少于50%的钢筋数量锚入地下连续墙墙体中，另外锚入长度还应根据受力要求来计算确定；正弯矩钢筋也需要锚入内衬内部，并不小于规范[15]规定的锚固抗浮梁长度.

图14 垂向位移曲线拟合图(基岩埋深92 m)Fig.14 Vertical displacement curve fitting(bedrock embedment depth:92 m)

地震时主体结构与抗浮梁震动步调基本保持一致，顶板处最大水平位移为0.086 3 m、最小水平位移为-0.090 3 m；抗浮梁的最大水平位移为0.085 5 m、最小水平位移为-0.090 1 m.

下面给出顶板和抗浮梁之间水平位移差图，如图16所示：地震时主体结构与抗浮梁最大水平位移差仅为2.88 mm，出现在地震持续过程的第33 s时刻.

3.2.5 不同地震动峰值加速度下的水平位移

如表5所列，给出在不同地震动峰值加速度下的水平位移统计数据，以便分析出不同抗震设防烈度及相应的构造措施下结构之间所发生的最大和最小位移值.

图15 抗浮梁与地下连续墙连接处最大正位移包络图Fig.15 Maximum displacement envelopment between anti- floating beam and underground diaphragm wall

图16 顶板及抗浮梁角点水平位移差Fig.16 Horizontal displacement difference between the top plate and the anti-floating beam

表5 不同地震动峰值加速度下水平位移统计表

如表5所列：在抗震设防烈度为7度条件下(地震加速度为0.143 1g)，结构最大水平位移为86.3 mm，顶板与抗浮梁最大位移差仅为2.88 mm；对于8度设防的抗震构造措施(地震加速度为0.20g)，其结构整体最大水平位移为133.61 mm，顶板与抗浮梁最大位移差仅3.6 mm，以上位移差均满足地下建筑抗震设计规范中的构造位移允许值的要求.

4 结论

本文运用时程分析法分析了该地铁车站结构在地震波作用下的动力响应特性，得出有关软土地区地铁车站结构地震响应的一些规律如下：

1) 在地震动载作用下，车站主体结构的位移以整体位移为主，地层、结构、抗浮梁的最大正位移在85.55～87.75 mm之间，最大负位移-103.43～-100.62 mm之间；在地质分层的土层中，土层弹性抗力系数存在有差异.结构除了发生整体位移之外，还发生了局部不均匀变形，该变形将导致结构发生一定的扭转.

2) 从垂向位移曲线拟合图看出，拟合出的天津市基岩埋置深度约为92 m，计算结果与理论结果拟合程度较好.由此可见埋深大小对地铁车站地震响应的影响幅度较大，在垂向上随着地下结构的覆土埋深越浅，压顶梁与顶板之间的位移值则越大，所受的震害也就随之增大.

3) 在7度烈度地震作用下，结构最大水平位移值绝对值约为86.30 mm，而主体结构与抗浮梁最大水平错位仅2.88 mm，抗浮梁能够很好地起到压顶抗浮的作用，不会出现因抗浮梁脱落而导致结构整体抗浮能力不满足要求的情况.