东坪基岩气藏气水相对渗透率的确定方法

罗 沛，杨 云，柴小颖，杨会洁，王 炯

1.重庆科技学院石油与天然气工程学院，重庆 沙坪坝 401331；2.中国石油青海油田公司勘探开发研究院，甘肃 敦煌 736202

引言

东坪气藏是中国发现的首个大型整装构造底水基岩气藏。投产初期单井产能高，但气井见水时间早，水侵规律复杂，导致气井产量大幅度下降，大量气井因水淹而停产。气水相对渗透率曲线是气藏产量预测、生产动态分析、开发指标计算和制定治水稳产对策的基础资料，通常采用稳态法或非稳态法实验测试得到。但该气藏储层非均质性极为严重，裂缝和局部溶蚀孔洞发育，表现为低孔、高渗、大渗透率级差的特点[1-2]。取芯资料表明，储层岩性复杂多变，风化破碎带岩芯松散，难以成形，而致密带几乎不渗透。岩芯无法进行驱替实验，至今尚无气水相对渗透率数据，成为困扰气田认识与决策的关键难题。此外，对于此类非均质性极强的储层，岩芯测试得到的相对渗透率曲线很难代表整个气藏的相渗特征。一般是通过相渗曲线的归一化处理获得储层的相渗曲线[3]。但归一化的相渗曲线同样受制于取芯位置和数量的限制，也不一定能够反映整个储层的整体渗流特征。两相相对渗透率曲线也可以通过理论计算得到。

由于压汞实验比稳态或非稳态驱替实验容易，因此，基于压汞曲线计算两相相对渗透率曲线方面的研究成果较多，计算模型就有10 多种。唐永强等[4]基于特定的实验数据，对各种计算模型进行了评价。李治平等[5]根据泊肃叶定律建立了基于压汞曲线计算气水相对渗透率曲线的方法，并引入迂回系数校正。王怒涛等[6]提出了一种用含水率数据计算油气两相相对渗透率曲线的方法，认为得出的相对渗透率更具代表性。马新仿等[7]应用分形几何原理，研究了低渗透储层岩石的孔隙结构，表明岩石的孔隙结构具有分形特征，孔隙结构的复杂程度和非均质性可用孔隙结构的分形维数定量描述，并根据毛管压力曲线计算了孔隙结构的分形维数。贺承祖等[8]基于分形几何理论，建立了毛管压力、J函数和相对渗透率的解析公式。何琰[9]、李中锋[10]、周克明等[11]基于压汞测试数据和分形介质理论，建立了两相相对渗透率的理论预测公式。李留仁等[12]研究了孔隙结构的球体模型和毛管数模型之间分形维数的关系，基于西峰油田压汞数据和毛管数模型，给出了分形维数与孔隙度、渗透率及均质系数等参数之间的关系，表明分形维数越大，储层物性越好。Li[13]基于压汞实验数据，分别采用Angulo-Gonzalez、Friesen-Mikula 和Brooks-Corey 模型计算分形维数，结果显示3 种方法具有较好的一致性，表明用分形维数能够评价岩石的非均质性。唐玮等[14]研究了东河1油田毛管压力曲线的分形特征，表明退汞曲线分形维数与均质系数等孔隙结构特征参数均有较好的相关性。这些研究为采用压汞曲线确定孔隙分形维数，进而采用分形理论计算相对渗透率曲线提供了新的思路和方法。Lei 等[15-16]基于分形理论，建立了多孔介质相对渗透率预测模型，通过与实验数据的对比，验证了预测模型的准确性，探讨了液膜厚度、孔隙结构参数和流体黏度比等参数对多孔介质相对渗透率的影响。Yu 等[17]建立了考虑裂缝弯曲度、孔隙面积、饱和度和孔隙微观结构等因素的裂缝性油藏分形相对渗透率函数。张涛等[18]建立了考虑气体滑脱效应、孔喉结构参数、含水饱和度分布的气水两相相对渗透率模型。莫邵元等[19]建立了考虑驱替压差影响的致密砂岩气藏气水相对渗透率分形模型。

基于分形介质理论预测两相相对渗透率方面已有较多的研究成果，但几乎所有理论计算模型均以压汞曲线确定的孔隙结构分形维数为基础，对于物性差异相对较小的砂岩储层具有较好的适用性。对于非均质性极强的基岩气藏，由于压汞曲线类型多样化，难以通过压汞曲线获得具有代表性的储层孔隙分形维数。本文提出一种基于生产水气比历史拟合方法，确定能够反映非均质储层整体渗流特征的孔隙结构分形维数，进而计算气水相对渗透率曲线。

1 东坪1 区基岩气藏储层介质特征

东坪1 区基岩气藏储层岩性以变质岩为主，存在少量的片麻岩。储集空间以成岩后生作用产生的溶蚀孔、溶蚀缝为主，伴有少量的构造缝。孔隙度分布在2.0%∼6.0%，峰值集中在3.0%∼4.0%，大于物性下限2.0%的孔隙度均值为4.5%。储层渗透率在0.10∼10.00 mD，均值为2.63 mD。东坪1 区储层的孔隙度、渗透率分布如图1 和图2 所示。

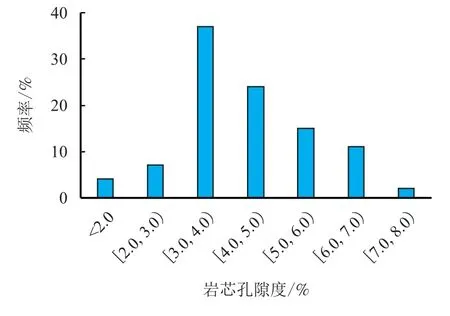
图1 东坪1 区基岩储层孔隙度分布图Fig.1 The porosity distribution of DP1

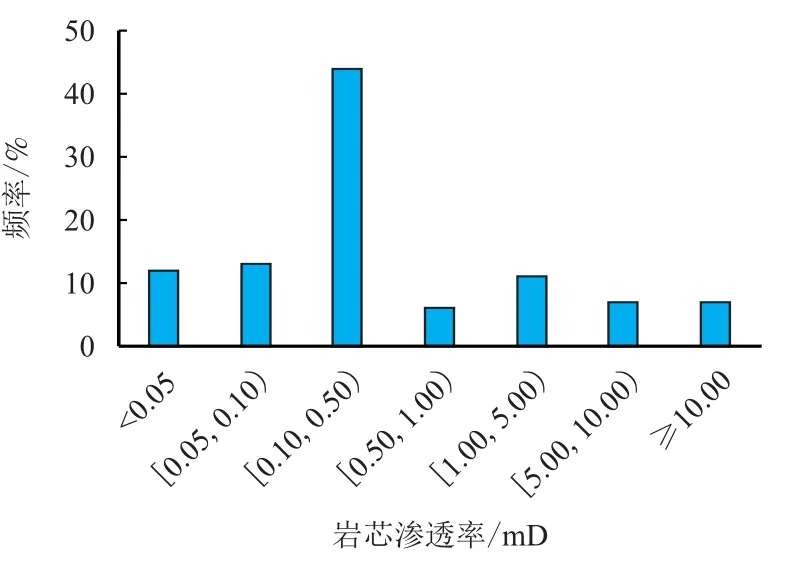
图2 东坪1 区基岩储层渗透率分布图Fig.2 The permeability distribution of DP1

由于基岩孔隙以裂缝和溶蚀孔为主，无裂缝和溶蚀孔洞段岩芯致密不渗透，而裂缝和溶洞发育段岩芯破碎不成形。因此，无法通过岩芯驱替实验获取气水相对渗透率曲线。据东坪1 区5 口井100 多块岩芯柱塞压汞实验数据分析，该区基岩储层非均质性强，喉道分布范围广。压汞曲线可分为4 类：I 类曲线（图3a）具有较长的平台段，分选性最好，均质性强。以细孔喉岩芯居多，孔隙度在3.0%∼5.0%，渗透率0.20∼2.00 mD，进汞饱和度最大（＞75%），饱和度中值压力在15∼70 MPa，退汞效率在15%∼30%。II 类曲线（图3b）呈陡度较大的直线，饱和度中值压力低，反映了分选性差，孔隙喉道分布范围广，孔隙度在3.0%∼4.0%，渗透率在1.00∼2.00 mD，最大孔喉半径与平均孔喉半径差别大。III 类曲线（图3c）表现为折线型，由粗细两种孔喉构成，以偏粗的歪度为主。平均孔隙度小于3.0%，平均渗透率小于0.50 mD。由于受岩芯中裂缝和大孔喉比例的影响，排驱压力变化范围较大，饱和度中值压力高（＞1 000 MPa）。最大进汞饱和度较低，接近或小于50%，退汞效率偏低（＜15%）。IV 类曲线（图3d）以偏细的歪度为主，兼有少量粗孔喉，平均孔隙度约2.5%，具有较低的排驱压力（＜5 MPa）和饱和度中值压力（＜30 MPa），为裂缝性致密岩芯。此外，尚有部分岩芯最大进汞饱和度很低（＜30%），最大进汞压力高于100 MPa，退汞效率接近零。反映储层致密，孔隙度2.0%左右，也可能因注汞压力过高而导致孔隙结构破坏。

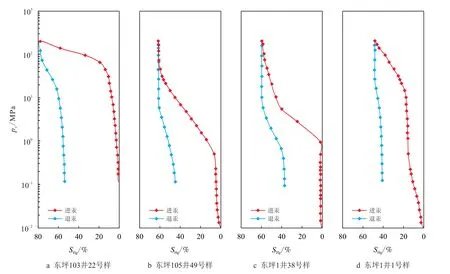
图3 东坪1 区基岩气藏压汞曲线类型Fig.3 The type of capillary pressure curves in DP1

从分类统计结果来看，II、III、IV 类孔隙结构居多，约占91%，I 类孔隙结构储层仅9%。表明储层岩石孔隙结构复杂，非均质性强。

2 气藏饱和度的确定

根据物质平衡原理，对于水驱气藏某一开发时刻应满足：累计采出天然气及地层水的地下体积=天然气的地下体积膨胀量+束缚水及岩石体积膨胀量+水侵体积。即

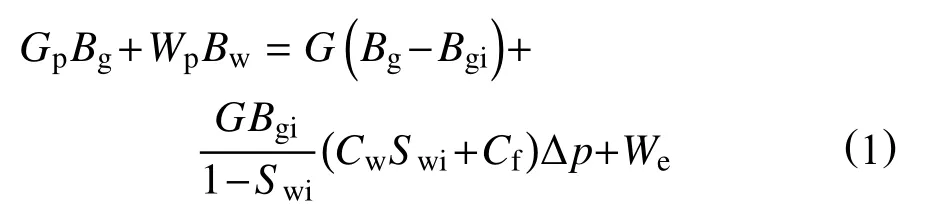
将式（1）改写成

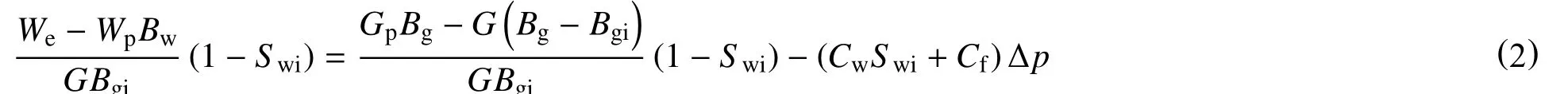
显然，式（2）左端为到当前时刻地层含水饱和度的增加量，此时，地层的含水饱和度为

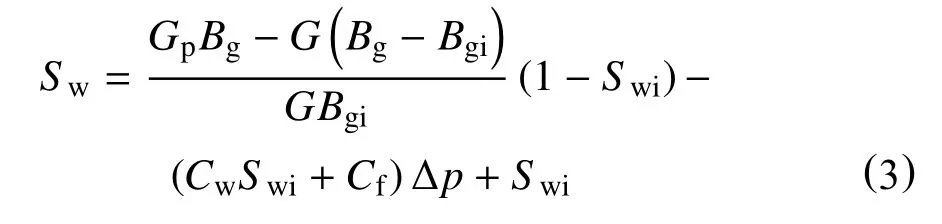
相对于气体的体积变化量，束缚水及岩石体积膨胀量很小，可以忽略，故有

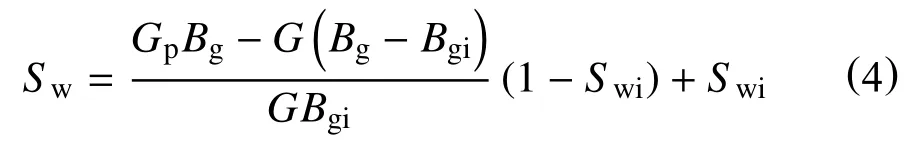
式（4）表明，对于水驱气藏，某一开发时刻，气藏中水的体积增加量近似等于采出气体的地下体积与气体地下体积膨胀量之差。

3 气水相对渗透率预测

对于气水同产气井，在考虑凝析水气比时有[20]

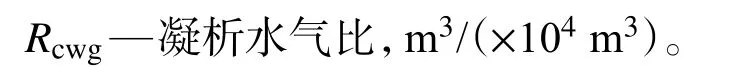
根据分形介质理论，气藏的含水饱和度、孔隙结构分形维数和气水相对渗透率关系为[8]

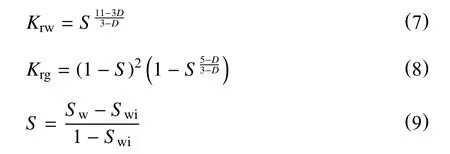
式中：

D—分形维数，无因次；

S—毛管压力下的润湿相饱和度，无因次。

由式（7）∼式（8）可知，只要确定了气藏孔隙结构的分形维数D，即可计算出不同含水饱和度下的气水相对渗透率。D值一般由压汞实验测得的毛管压力曲线计算[8]。

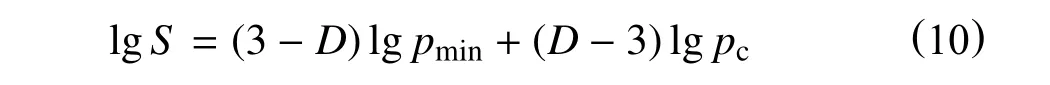
式中：

pc毛管压力，MPa；

pmin储层中最大孔隙半径对应的毛管压力，MPa。

作毛管力与含水饱和度双对数曲线，获得其斜率m，则

由于东坪1 区气藏储层岩石压汞曲线类型多，变化大，大部分压汞曲线表现为弧线或折线，因此，难以确定具有代表性的孔隙结构分形维数。为了确定该气藏储层孔隙分形维数的界限，选择最具代表性的I 类（对应最小的分形维数）和II 类（对应最大的分形维数）岩芯压汞曲线，分别根据式（9）∼式（11）进行回归分析，获得该区的分形维数介于1.77∼2.76，回归曲线如图4 和图5。

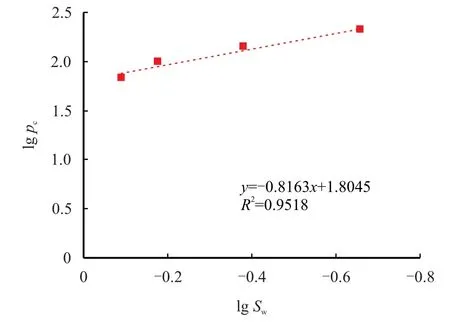
图4 I 类压汞曲线分形维数分析图（103 井22 号岩芯）Fig.4 The fractal dimension by capillary pressure curve of type I（Core 22 of Well 103）

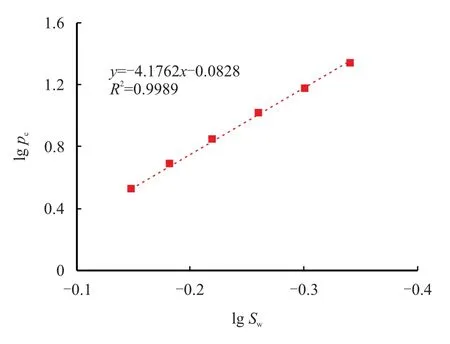
图5 II 类压汞曲线分形维数分析图（105 井49 号岩芯）Fig.5 The fractal dimension by capillary pressure curve of type II（Core 49 of Well 105）

压汞曲线确定的孔隙结构分形维数仅代表了岩芯周围储层的孔隙结构，显然，对于岩性变化较大的非均质储层，这种方法无法获取代表整个气藏储层岩石平均特性的分形维数。而气藏的生产数据反映了气藏储层的整体特性，故采用生产水气比历史拟合法。通过在一定范围内假定一系列分形维数，计算气水相对渗透率，进而计算理论生产水气比曲线，与实际生产水气比曲线进行拟合，对应于误差最小的分形维数即为能够代表储层整体孔喉特征的分形维数，由此计算气水相对渗透率曲线，具体步骤如下。

（1）根据气藏不同开发时刻的地层压力，计算气体的黏度和体积系数。

（2）由式（3）或式（4）计算该时刻的储层含水饱和度。

（3）根据压汞曲线分析，确定D值范围，由式（6）∼式（9）计算理论生产水气比，与实际生产水气比数据Rwg(j)进行历史拟合，确定D值。拟合目标函数为

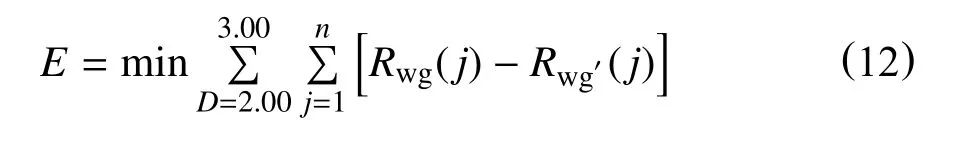
式（4）由式（7）和式（8）求出不同饱和度下的Krg和Krw，作相对渗透率曲线。

4 东坪1 区基岩气藏气水相对渗透率

东坪1 区基岩气藏除了东坪1 井具有6 次静压测试数据外，其他井的静压测试数据只有1∼2 次，难以准确确定整个气藏开发过程中的压力变化，但根据各井原始地层压力和构造特征来看，整个气藏属于同一个压力系统，故以东坪1 井不同开发时刻的实测地层静压近似代替东坪1 区的地层压力，取复算后的原始地质储量72×108m3，原始地层压力43.87 MPa，束缚水饱和度为22.6%，计算凝析水气比[16]为0.119 m3/（×104m3）进行分析。东坪1 区不同开发时刻的地层压力与累计产气量、累计产水量变化曲线如图6。

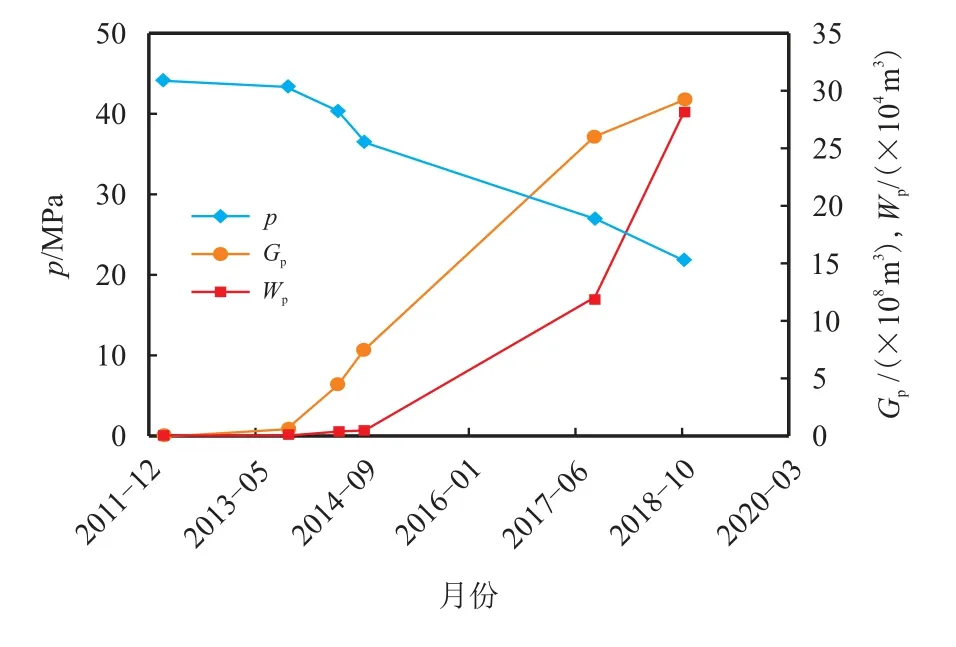
图6 东坪1 区生产数据及地层压力变化Fig.6 Production rate and static pressure of DP1

根据气藏的累计产气量和累计产水量计算生产水气比Rwg(j)，选择分形维数的拟合区间为1∼3，步长为0.01，计算理论水气比(j)，与实际水气比进行历史拟合，当分形维数为2.10 时误差最小。由该方法确定的分形维数正好介于采用压汞曲线计算的分形维数范围内，拟合曲线见图7。

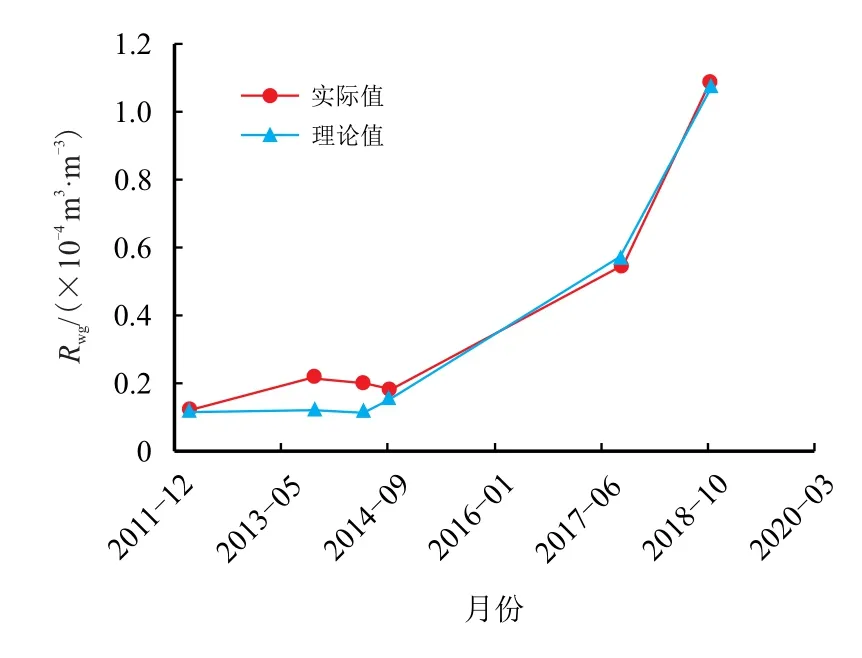
图7 东坪1 区生产水气比拟合图Fig.7 Rwghistory matching plot of DP1

从生产水气比拟合效果来看，开发初期拟合效果不佳，其原因是该气田开发初期由于计量设备问题导致产气量记录不准，此外，导致开发初期生产水气比高的原因可能来自钻井、完井及压裂过程的侵入水。

分别取分形维数为1.77、2.10 和2.76，计算得到东坪1 区的气水相对渗透率曲线如图8。图8 中间一组曲线（对应于D=2.10）为通过生产水气比拟合所得的分形维数所计算的相对渗透率曲线，反映了东坪1 区基岩储层的整体渗流特征。相当于实验室测定的各类储层相对渗透率曲线的归一化处理结果。当应用要求较高时，可根据目标井所在区域岩芯压汞曲线所获得的分形维数计算所得的相对渗透率曲线。如：均质性较好的I 类区域（103 井区）选择图8 中最左侧的一组曲线（对应于D=1.77），而非均质性较强的II 类区域（105 井区），则选择最右侧的一组曲线（对应于D=2.76）。

由图8 可以看出，随着分形维数的增大，等渗点向右下方偏移。意味着在相同的饱和度下，气相的相对渗透率增大，水相的相对渗透率降低。其原因是，分形维数越高，孔隙喉道越小，毛管结构越复杂。在相同的地层含水饱和度下，更多的细小孔隙被水占据，而细小孔隙中的毛管力更大，导致水相相对渗透率降低，两相的有效渗透率损失增大，相反，相对较多的大孔隙留给了气相，导致气相渗透率增大。因此，储层非均质越强，则气藏水淹后更容易发生水锁。

5 结论

（1）基于储层孔隙分形维数和生产历史拟合相结合的气水相对渗透率计算方法，为无法进行岩芯实验测试的气藏提供了一种有效途径。

（2）对于严重非均质储层，实测相对渗透率曲线变化大，采用生产历史拟合方法确定的相渗曲线能够反映储层的整体渗流特征，因此，更具代表性。

（3）该方法的关键在于确定不同开发时刻储层的含水饱和度，饱和度计算的准确性受地层平均压力和原始地质储量的影响，因此，当气藏的储量不确定或因开采不均衡导致地层压力难以确定时应慎重使用。