基于智能算法的油气田地应力三维预测

袁 多，吴 超，卢运虎，张东清

1.页岩油气富集机理与有效开发国家重点实验室，北京 昌平 102206

2.中国石化石油工程技术研究院，北京 昌平 102206

3.中国石油大学（北京）石油工程学院，北京 昌平 102249

引言

油气田地应力三维预测是将已钻井的地应力信息延拓外推至区域地层空间的运算过程，亦称地应力空间建模，它有助于准确认识地应力在三维区域内的纵、横向分布规律，从而在井壁失稳控制、套管损伤和出砂预防、压裂工艺优化等方面发挥指导作用[1-2]。由于油气储层埋藏相对较深，钻井与开发工程所涉及的地层空间范围较广，其多变的沉积与构造环境导致了地层具有复杂的岩石物理和力学特征，因此，针对油气田地层空间进行地应力预测具有更大的难度。

在油气田多种数据资料中，可用于较准确求取地应力的信息主要为实验测试数据以及与应力存在直接关联的声波测井、密度测井等数据，这些信息都分布于工区内的完钻井处。因此，油气田岩层空间的地应力建模以完钻井的测试和测井资料为基础，在三维区域内的地质力学和地球物理信息约束下，运用数学手段将单井地应力数据推广为三维空间的地应力数据体[3]。事实上，这种面向未钻地层的地应力预测对于后续钻井的指导意义更为重要。

通过岩芯和压裂实验可精准确定地应力大小[4-5]，但油气田深层取芯和测试费用较高，且只能获得井点个别深度的应力信息。因而利用测井资料进行分层地应力计算应用更为广泛，其中基于地层各向同性假设的求取方法包括早期单轴应变法、黄氏方法、组合弹簧法、Holbrook 法和葛氏方法等[6]，近年各向异性模型也得到了完善[7-8]。由于资料来源制约，测井分析方法通常在钻后进行，而且它只能反映井壁围岩应力状况，对于油气工程尤其是钻井的指导缺乏时效性和针对性。赵海峰等提出了利用实钻资料反演地应力的方法，但这类井周应力实时监测技术无法用于区域地应力预测[9]。对于油气田地应力的三维预测问题，当前常规处理手段是借鉴矿业、水利等学科的地应力反演理论[10]，将测试、测井数据和有限元模拟等数值算法结合起来进行地应力预测[3，11-13]，但在建模计算中没有使用三维地震信息进行约束控制，地应力预测精度和分辨率难以满足精细勘探开发的需求。刘建伟等基于叠前弹性反演理论进行了页岩油藏地应力的三维地震预测[14]，但资料处理和计算量的限制导致该技术在地层比例超过90%的非目的层难以推广应用。近期有学者尝试使用叠后地震数据预测三维地应力以提高运算时效[15-17]，但其操作步骤繁多，且用于应力解空间搜索的全随机算法易陷入局部最优，求解效率有待提高。斯伦贝谢公司的地震指导钻井技术（SGD）中通过地震层析反演预测强度、应力、压力等地层力学参数[18-20]，同样由于运算量的制约，该方法仅针对钻头前方的小范围空间。

本文通过考察岩石物理力学参数与地震信息之间的关系，针对不同的工况条件，运用BP 神经网络、模拟退火等智能算法建立了一套较全面的油气田地应力场三维预测技术体系。该技术充分利用地震信息覆盖面广、信息量大的优势，以提高地应力预测精度和分辨率，同时通过优化算法和处理流程来提高操作性能。

1 间接预测法及其应用实例

根据地震勘探理论，叠后地震记录数据可以表示为各套地层界面处的反射系数和地震子波的褶积，即

地震波反射系数通过反射界面两侧介质的波速和密度来计算

一般说来，地层纵波速度和密度之间存在良好的经验关系

由式（1）∼式（3），可以将叠后地震记录和层速度之间的关系表示为如下函数关系

众所周知，岩石的弹性模量和泊松比数值由地层密度与声波速度决定

大量岩石物理实验结果表明，岩石纵波和横波传播速度之间存在一定的经验关系

目前国内外已提出多种油气田地应力分层计算模式，各类模式中普遍涉及的影响因素为弹性模量、泊松比、孔隙压力及构造应力系数，以得到广泛使用的黄氏修正模式为例

利用密度测井数据积分可得到适用于目标工区的上覆压力模式，构造应力系数通常由实验室或现场测试结果拟合得到，孔隙压力与声速关系非常密切，常用的Eaton 计算模式

根据式（5）∼式（8），层速度与地应力之间的函数关系可表示为

通过式（9），可以发现用于地应力建模的最关键、最基础的数据是地层的纵波传播速度。式（4）已表明层速度和叠后地震记录之间存在定量关系。

因此，可以运用数学方法通过对地震数据反推求得速度信息，这在地球物理学中称为地震速度反演。传统的反演过程是基于Levenberg-Marguardt理论求取层速度的最小二乘解[21]，而式（4）在解析构建偏导数矩阵时巨大的工作量大大降低了运算时效，且初始解选取的严格性也难以保证稳定的迭代过程。

考虑到BP 神经网络在模式识别、数值逼近、分类等智能学习方面具有很高的稳定性与可靠性，因此笔者使用这种多层前馈网络算法来识别层速度和地震记录之间的函数映射关系[22]。

首先，收集工区完钻井的声波测井及井旁地震记录，建立时深关系以将地震、测井数据统一标度，并从地震记录中提取瞬时参数、频谱参数、功率谱参数、自相关参数、自回归参数、分形参数等特征参数等。

分层段运用聚类算法将地震特征参数和声波速度建成学习样本对，并将其分别导入BP 神经网络的输入和输出端。

基于激励函数，利用式（10）依次计算网络各节点（神经元）的输出

设置目标函数使网络输出声波速度和学习样本对中的实测速度值之间达最小误差，选取目标函数E0，运用梯度下降法对网络连接权值与阈值逐次迭代修改

重复以上运算直到某次计算的E0达到指定精度，可结束网络学习过程。

基于上述分层学习成果，将工区内未钻空间位置处的地震特征参数按照对应的地层输入BP 神经网络，输出得到相应位置的层速度预测值，即可建立层速度的三维空间数据体。

在预测三维层速度的基础上根据工区实际地质情况选取力学模型进一步预测区域地应力[6-8]。上述思路是在层速度地震反演的基础上进一步预测地应力，因此称之为间接预测法。由于该方法所需的学习样本和经验参数较多，其应用条件是工区具有丰富的实测资料用于参数统计回归及BP 神经网络学习。为尽量避免BP 神经网络陷入局部极值，借鉴了Matlab 工具函数trainbfg 采用的基于拟牛顿法的训练算法，实际收敛速度和精度均很理想。

渤海湾某油田断块发育，地应力状态复杂，井壁失稳、出砂、套损等复杂故障频繁发生。

由于该油田LZ 工区完钻井实测信息丰富，所以在该工区应用了间接预测法进行地应力三维预测。通过实测数据的统计分析，确定了模型参数，其中工区分层构造应力系数见表1。

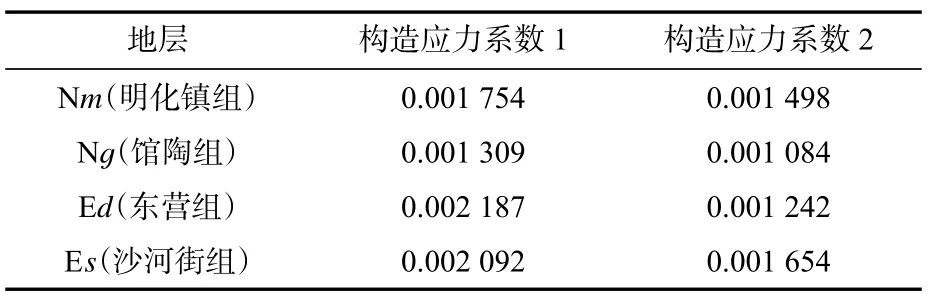
表1 LZ 工区分层构造应力系数Tab.1 The tectonic stress coefficients of different strata in LZ Area

收集到LZ 工区的三维叠后地震数据体，图1显示的剖面是其中的line1518，基于BP 神经网络算法预测三维层速度，图2 显示的速度剖面是其中的line1518，进一步预测三维地应力（图3）。

图1 LZ 工区的叠后地震数据体Fig.1 Post stack seismic data volume in LZ Area

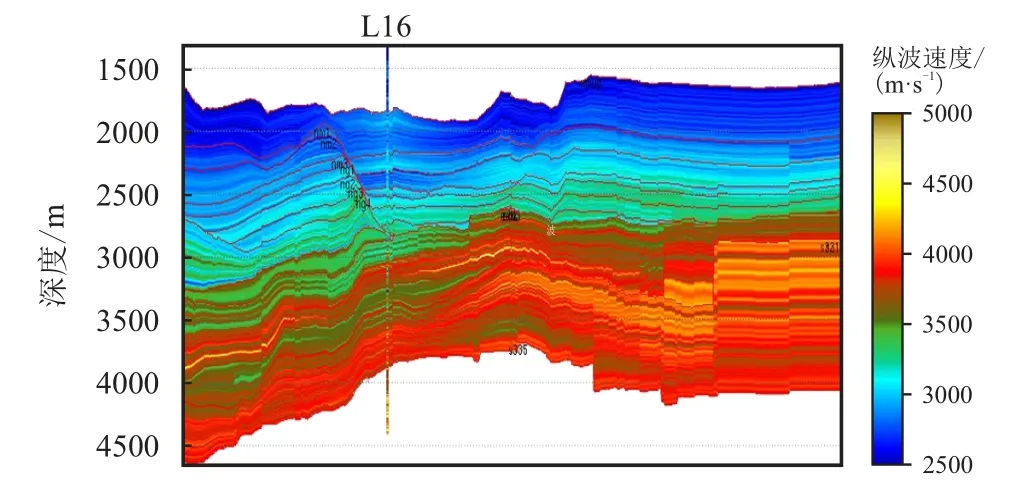
图2 基于BP 神经网络算法预测LZ 工区纵波速度数据体Fig.2 Predicted interval velocity data volume based on BP neural network algorithm in LZ Area

图3 预测得到的LZ 工区最大水平地应力数据体Fig.3 Predicted maximum horizontal stress data volume in LZ Area

图4 和图5 为从地应力数据体中切片得到的分层段横向展布等值线图。

由等值线图可发现LZ 工区地应力呈从北向南逐渐增大的区域特征，另外可通过观测地应力等值线密集程度来大体确定工区断层的走向[11]，可判断L22、L16、L36、L32、L3-3 等井附近发育5 组断块（以上推断与地质认识基本吻合）。以上分析成果可用于后续钻井的井壁失稳、出砂、套损预防及开发方案优化设计。

2 直接预测法及其应用实例

在工区完钻井数量与实测数据较少的情况下，运用间接预测法可能存在一些问题：（1）井点处可信的测试信息缺乏，式（7）中的构造应力系数难以合理确定。（2）用于建立学习样本的测井资料较少，导致BP 神经网络模式识别及外推能力减弱。针对以上问题，可以考虑变换思路，由式（9）反推，建立以地应力及构造应力系数为自变量的函数关系式

将式（12）和式（4）结合，可以导出

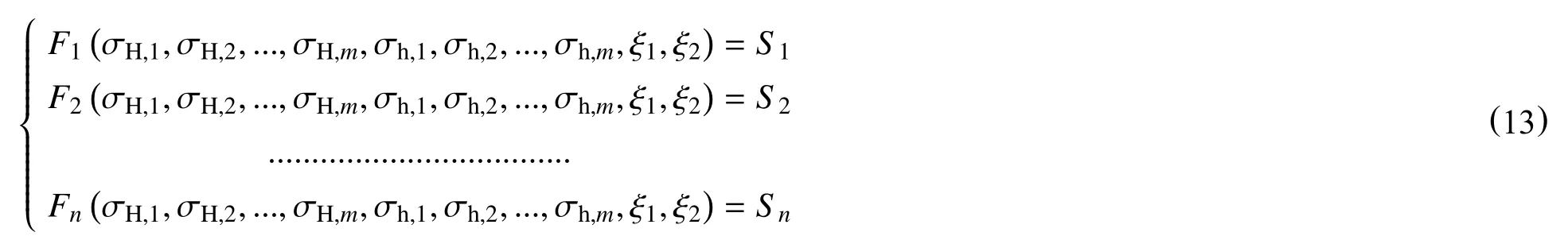
式中：n每个地震道上地震记录序号；

m每个地震道上待求解的地应力对应的反射界面序号；

Sn每个地震道上的各个地震记录。

式（13）是一个地震道上的以地应力及构造应力系数为未知量的非线性方程组，可根据其通过地震数据直接反演求取三维区域内各地震道上的水平地应力解向量，也可同时解得构造应力系数。

理论上可以使用非线性优化理论求解式（13），通过寻求合成与实际地震记录的最优匹配来直接求解地应力，避免经验系数不准确引起的误差，因此称之为直接预测法。

但在井点实测信息缺乏的情况下，若按照常规的非线性最小二乘法求解式（13），将会因为方程组规模大、非线性程度高、测井插值所得的初始解质量较差而导致求解过程稳定性极差、运算时间过长，所以笔者考虑使用智能优化理论中的模拟退火算法对其进行求解。

在完钻井资料缺乏的工况下，利用该算法求解式（13），具有两个突出优点：（1）对初始解要求不严格，概率重要性采样算法可以保证稳定的寻优运算过程。（2）在地震道上进行全局寻优，减少得到局部最优解的可能性。模拟退火属于智能算法，它模仿固体的退火过程，在缓慢降温时每个温度下内部粒子达平衡态，最终降至低温时内能最小[23]。根据式（13）的求解要求，设定目标函数。

同时设置模拟退火过程的初始温度T0、最低温度Tf，温度降低策略采用常规的Tj+1=λTj（0 ＜λ ＜1，j为降温次数）。具体运算过程如下：

计算并分析工区完钻井的水平地应力数据，统计其所服从分布类型（一般为正态分布），确定各参数候选解搜索邻域空间并建立各自的分布密度函数，以随机方式产生某地震道上的初始解σ0，并在此后迭代过程中对解空间的随机采样，逐次获得候选解。

在初始温度下T0，计算初始解目标函数Φ0，然后在邻域内随机产生一个候选解σ1，计算其目标函数Φ1。

如果Φ1≤Φ0，则接受σ1为当前最优解；否则需计算（K--Boltzmann 常数），并产生一个随机数R∈[0，1]，并运用Metropolis 准则：若P＞R，则也接受σ1为当前最优解，否则不接受σ1。

在初始温度下反复产生候选解，并按上述方式不断更新当前最优解。

当连续若干步目标函数值无明显变化或候选解搜索次数达到设定马尔可夫链长度L，该温度下的迭代运算结束。

按照降温策略逐次降温，每个温度Tj下均执行上一步的操作（需注意计算P时需更新Tj）。

直至温度降低至最低温度Tf或连续两次搜寻到的最优解之差小于指定容差ε，全部迭代寻优运算结束，得到本地震道上的水平地应力最终优化解，进入下一地震道重复以上求解过程，直至解得三维岩层空间上的地应力值。

必须说明的是，式（13）的求解涉及到地层密度、上覆压力、孔隙压力计算模式中的经验系数，求取这些系数相对容易，且通用性好，因此不再作为未知量参与求解。

但由于在直接预测法中没有事先预测层速度，即无法通过层速度进一步预测孔隙压力，而孔隙压力又是式（13）求解的必需参数，所以可参照上述地应力直接求解的思路，利用地震数据先期求取孔隙压力。

与式（13）的推导过程类似，直接通过地震信息求取孔隙压力

式（14）的求解过程和式（13）基本一致，这里不再赘述。在求得三维孔隙压力数据后，将其作为求解方程组（13）的已知信息。

式（13）和式（14）的求解需要分地层进行，对于同套地层，构造应力系数作为固定值参与求解。

油田的NP-2 工区属新探区，岩芯与现场测试及测井数据较少，前期使用有限元建模得到的地应力平均计算误差约22%，因此，在该工区引入了地震信息进行区域地应力计算分析。

图6 为NP-2 工区的三维叠后地震数据体（以其中201 地震测线为例对其二维剖面进行显示）。

图6 NP-2 工区的叠后地震数据体Fig.6 Post stack seismic data volume in NP-2 Area

在运算设计时，充分考虑了快速模拟退火策略[24-25]，以期提高其现场应用时的运算速度。

经过迭代运算后通过地震信息直接得到了最大和最小水平地应力三维数据体（图7、图8）。

图7 NP-2 工区预测最大水平地应力数据体剖面Fig.7 Predicted maximum horizontal stress data volume in NP-2 Are a

图8 预测得到的NP-2 工区最小水平地应力数据体Fig.8 Predicted minimum horizontal stress data volume in NP-2 Area

图9 和图10 分别为从三维地应力数据体中切片得到的分层段横向展布等值线图。

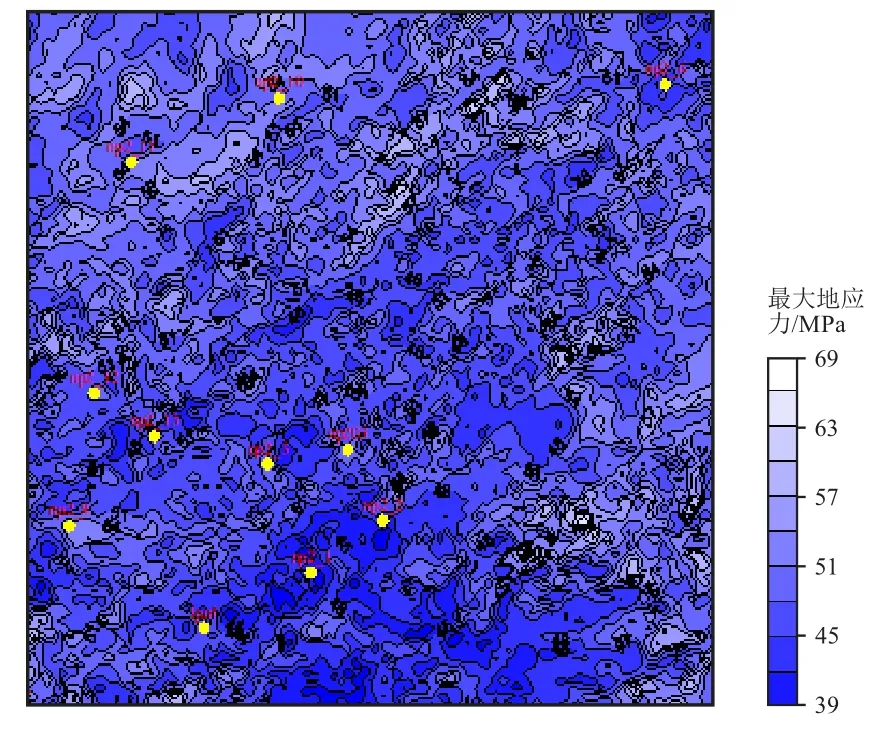
图9 NP-2 区块Nd1 段最大水平地应力切片等值线图Fig.9 Slice contour map of maximum horizontal stress of Nd1 Section in NP2 Area

图10 NP-2 区块Ng2 段最小水平地应力切片等值线图Fig.10 Slice contour map of minimum horizontal stress of Ng2 Section in NP-2 Area

从图上可发现，NP-2 工区地应力具有北部大、南部小的整体特征，同时从等值线疏密程度判断出NP2-13、NP2-2、NP2-10 井附近发育3 组次级断层，且大体呈NE45°走向，实际地质勘探成果验证了以上推断。上述间接和直接预测方法在该油田5 个工区根据实际工况进行了选择应用，在LZ、MYL、GSP 等老工区应用了间接预测法；而NP-1、NP-2 是新探构造，适用直接预测法。为了全面验证预测结果，从各工区的实际测试结果中取出部分样本，它们不参与经验参数统计拟合，仅作为验证数据，将其与相同空间位置处的预测值进行对比。从表2 可以看到，地应力整体预测精度基本可满足工程需要，其中直接预测法的计算精度总体上低于间接预测法，因直接预测所使用的约束信息相对较少，但其平均预测精度为90.73%，仍明显高于单纯力学建模方法（78.00%），同时剖面和切片图也可达到较高分辨率。

表2 多个试验工区预测与实测地应力数据对比Tab.2 Comparison between predicted and measured in-situ stress data of several test areas

另外，通过与前期试用过的叠前地震预测算法对比，本技术合理利用了叠后地震信息，在现场应用中的资料处理和计算量大大减少，优化求解运算过程稳定，操作流程更为简便，不仅可用于钻前地质力学特征综合分析，还可用于随钻井壁稳定预测。以上情况表明，该预测技术在油气田现场应用具备较高的适用性和可靠性。

3 结论

（1）地层声波传播速度是进行油气田地应力定量分析的基础数据，而叠后地震记录与层速度之间存在着非线性函数关系，因此，可运用智能算法解析这种关系，从而利用区域地震资料预测三维地应力。

（2）对于完钻井数量较多、实测信息较丰富的工区，其区域地应力计算适用间接预测法，该方法运用BP 神经网络算法识别完钻处的声波测井和地震信息之间的关系，并根据其外推预测三维层速度；同时利用测试数据统计相关岩石物理和力学经验参数，基于以上工作进行地应力三维预测。

（3）在工区测试和测井资料较缺乏的情况下，应使用直接预测法进行地应力三维建模，该方法以地应力和地震记录之间的映射关系为基础，运用模拟退火算法直接搜寻合成与实际地震记录达最优匹配下的地应力解向量，寻优运算过程稳定，易于得到全局最优解。对多数探区来说，本方法更具意义。