新加坡富时中国A50股指期货的波动溢出效应研究
霍 林 黄俊杰
(广西大学,广西 南宁 530004)
一、引言
2006年9月5日新加坡推出境外首支以中国A股为标的的股指期货——富时中国A50股指期货(原名“新华富时中国A50指数”)。由于富时中国A50股指期货与中国A股市场的交易时间存在差异,富时中国A50股指期货也被投资者当作中国A股价格走向的风向标。可见,检验富时中国A50股指期货与股指现货市场间的价格关系具有重要的现实投资指导意义。对此当前富时中国A50股指期货对A股市场在价格引导方面的表现如何?不同阶段的价格关系是否相同?不同频率的价格波动幅度是否存在显著的差异?这些问题都有待解决,全球新冠肺炎疫情加剧了金融市场的波动,若投机资本通过股指期货的杠杆效应在两个市场之间进行投机,将会加剧中国A股市场的波动。因此,系统分析新加坡富时中国A50股指期货与股指现货之间的波动溢出效应,对于投资者对冲A股的投资风险、市场监管机制建设具有重要的研究价值。
二、文献综述
从相关文献来看,国内外学者经过研究发现期货价格能够对市场信息反应迅速,Hasbrouck(1995)发现期货能够引导市场价格走势,如果这种价格走势趋于合理,则说明其更具有价格发现功能。为检验这一功能,国内外学者普遍采用ADF方法对期货和现货价格时间序列展开平稳性检验,并通过协整检验决定模型的选择,对期货与现货进行价格引导关系检验(Ghosh,1993;谢世清和杨雯婷,2018)。与此同时,有学者发现期货和现货市场间存在一定的价格波动,而这种价格波动来自其自身或者其他市场波动的影响。对此,国内外学者对这种波动溢出效应展开大量的研究,Engle(1982)提出ARCH模型之后,Bollerslev(1986)在ARCH模型基础上发展出GARCH模型,GARCH模型成为学者研究波动溢出效应问题的有力模型。Tao&Green(2012)基于DCC-TGARCH模型发现股指期货与现货之间不仅存在波动溢出效应,而且还存在非对称效应。同时,Karagiannis(2014)发现期货市场与现货市场之间的传导并不是单向的,而是会产生双向的波动溢出效应,且不断影响着两个市场的波动性。
当前学者的研究主要聚焦于股票市场与其他商品市场之间,在股指期货与现货市场方面的研究结论大相径庭。陶利斌等(2014)、陈焱等(2013)发现其中一个重要的原因就是选取数据的频率不同。吴国平和谷慎(2015)基于日数据研究发现,股指现货市场对股指期货市场存在波动溢出效应,但股指期货市场对股指现货市场并不存在该效应。朱莉和高鹏(2016)基于1分钟高频数据,则发现股指现货市场与股指期货市场存在双向的波动溢出效应。但田冰等(2019)研究后发现,股指期货与现货之间的传导也会由双向波动溢出转为单向的波动溢出。当前对富时中国A50股指期货的研究文献较少,且多是基于日数据分析为主,同时大多文献是将价格发现与波动溢出功能分开研究(武佳薇等,2019)。鉴于此,本文先检验两者之间价格引导关系,其次再深入分析多频数据下两个市场的波动溢出效应。
综上所述,本文的主要贡献在于:一是通过VECM模型与Granger因果检验分析在不同期货交易制度“松绑”时期内,富时中国A50股指期货与股指现货之间的价格引导关系;二是为更加精准地量化两个市场价格波动的交互作用程度与时间特征,运用非对称的BEKK-GARCH静态模型和DCC-MVGARCH动态模型多角度分析股指期货与股指现货市场的波动溢出效应;三是基于5分钟、15分钟、30分钟、60分钟高频数据以及日数据,对比分析不同频率下的两个市场关系差异性,有助于中国国内金融市场的稳定发展,同时有助于帮助投资者更全面客观地了解两个市场的价格引导关系以及波动溢出效应,在不同节点采取不同策略,从而达到套期保值或者投资的目的。
三、研究设计
(一)研究模型
1.BEKK-GARCH模型。针对股指期货价格的波动影响关系,国内外学者通过采用GARCH类模型展开研究,模型中的条件方差和条件协方差可以判定这种波动来源。鉴于此,本文在此基础上,通过两种多元GARCH模型对富时中国A50股指期货与股指现货的价格波动深入分析。在前人学者的研究基础上,Engle&Kroner(1995)提出BEKK-GARCH模型。该模型能够从静态角度分析两者的波动溢出效应和波动持续效应,且需要估计的参数减少。构建收益率时间序列滞后p阶的向量自回归VAR模型如公式(1)所示:
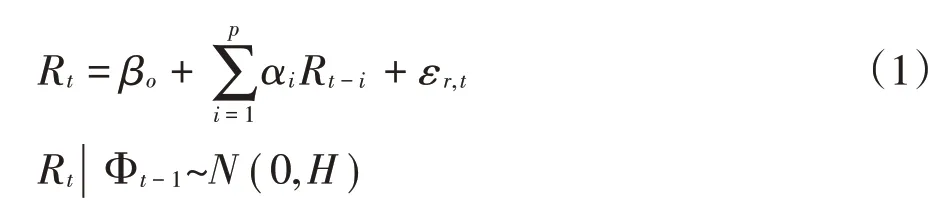
其中,Rt为收益率时间序列,βo为收益率均值,εr,t为收益率的残差项,Ht是条件协方差矩阵。
Bollerslev(1992)认为GARCH(1,1)可以充分捕捉数据中的聚集性特征。因此,为分析富时中国A50股指期货与股指现货之间的波动溢出效应,本文选择二元GARCH(1,1),构建BEKK-GARCH模型;由于股指期货与现货市场中容易出现非对称波动现象,即负收益往往在下一期的冲击大于正收益带来的冲击,如果忽略这种非对称效应会对模型的精度产生一定影响。因此,本文在BEKK-GARCH模型中加入非对称项,Ht则可以进一步设定为公式(2):
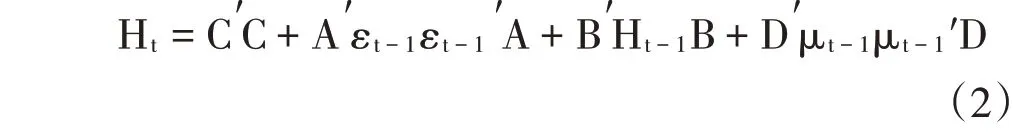
上式中,Ht=,A=,主对角线的hii表示收益时间序列的条件方差,非主对角线的hij表示收益时间序列的条件协方差,αii和bii刻画时间序列受自身ARCH模型和ARCH模型波动的影响;本文中A和B的对角线参数分别刻画股指期货收益率序列对股指现货收益率序列的ARCH模型和ARCH模型的波动溢出效应。由此,本文研究主要通过观察αij和bij是否显著不为0以检验波动溢出效应,若显著不为0,则说明存在波动溢出效应;μi,t为非对称项,代表好坏消息对市场波动的不同冲击,具体表达式为μi,t=max(εi,t,0),i=1或者2,系数矩阵D反映好坏消息冲击引起的非对称效应大小程度。
2.DCC-MVGARCH模型。由于静态的BEKKGARCH模型无法捕捉到不同市场之间的动态特征,本文进一步采用Engle(2002)提出的动态条件相关模型(DCC),其后演变成为多元广义自回归条件异方差模型(DCC-MVGARCH)。DCC模型相对于固定相关系数的CCC模型,能够测算两者动态协方差矩阵,更加符合股指期货与股指现货的动态相关性的实际特征,并能够验证两者的相关性是否随时间变动而变动。基于BEKK模型中的条件方差与协方差矩阵Ht做进一步假设,具体公式如公式(3)所示:

其中,Rt为条件相关系数矩阵,Dt为条件方差对角矩阵,基于单变量GARCH模型的时变条件标准差所构成的对角矩阵如公式(4)~(6)所示:
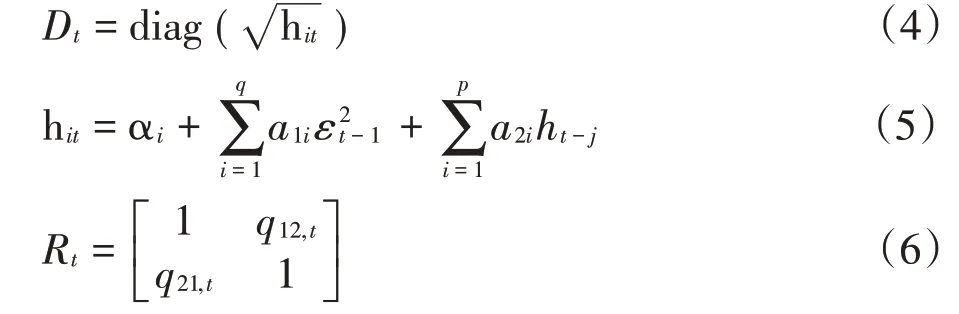
hit为条件方差,εt~N(0,Rt)是收益向量的标准化残差,Rt为标准化收益εt的条件相关系数矩阵,将Rt分解为公式(7)~(8):
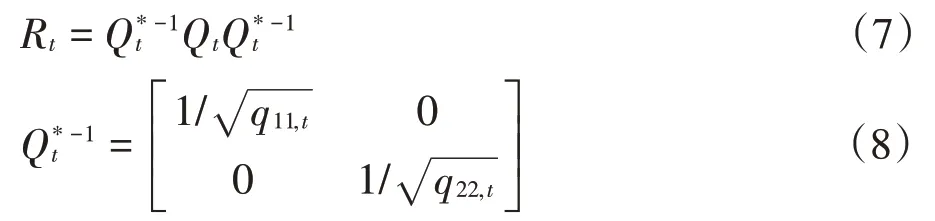
其中,Qt为标准化残差的时变协方差矩阵,为Qt对角元素的平方根矩阵,进一步可以得到DCC(1,1)模型,如公式(9)~(10)所示:
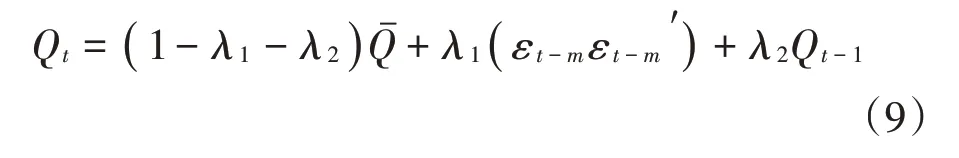

上式中,ρij,t为动态条件的相关系数,为第一阶段估计得到的标准化残差的非条件协方差矩阵,为对角矩阵,其对角元素为Qt对角元素的平方根,模型可以保证Rt是正定矩阵;参数λ1和λ2皆为非负数,决定整个动态过程,且有0≤λ1+λ2<1。
(二)数据的选取和指标说明
1.数据说明。本文采用新加坡富时中国A50股指期货与股指现货的数据,数据来自Wind数据库。日数据选取区间为股指期货成立日2006年9月5日至2020年9月30日,基于日数据探索不同时期内的富时中国A50股指期货与股指现货之间价格引导的关系;同时以国内关于股指期货“松绑”为关键时间节点,探究5个不同股指期货与股指现货之间的价格引导关系。第一次“松绑”是在2017年2月16日,第二次“松绑”则发生在2017年9月15日,第三次“松绑”是在2018年12月3日,第四次“松绑”是在2019年4月22日。此外,选取2020年4月1日至2020年9月30日的5分钟、15分钟、30分钟和60分钟的高频数据对比分析不同频率下的波动溢出效应。由于富时中国A50股指期货的交易时间与国内A股交易时间有所差异,因此本文基于富时中国A50股指现货进行数据匹配。其中,采用Ft表示富时中国A50股指期货的收盘价,将价格数据对数化处理后得到公式(11):

St表示富时中国A50股指现货的收盘价,同理将价格数据进行对数化处理后得到公式(12):

通过价格序列采用对数一阶差分方式可转化为收益率Rf,t与Rs,t时间序列,如公式(13)所示:
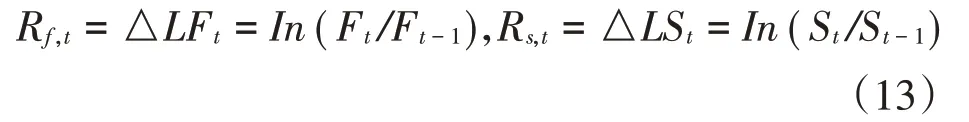
2.描述性统计。如图1所示,富时中国A50股指期货与股指现货的日价格趋势高度一致,且不同时期内的波动较大,2014年之后价格序列保持波动上升的趋势;从收益率的时间趋势图可以看出,富时中国A50股指期货与股指现货波动在不同时期具有明显差异性,且都存在一定的波动性聚集。
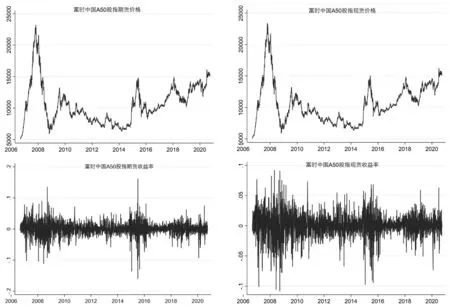
图1 富时中国A50股指期货与股指现货日收盘价格与日收益率时间趋势
从表1不难发现,5分钟数据收益序列的方差最小,日数据收益序列的方差最大,可见波动剧烈程度与时间跨度有关;从偏度和峰度来看,收益率序列中呈左偏状态的只有日收益序列,其他频率的收益序列均呈现为右偏状态,且最低的峰度系数大于5.485,数据频率越高,峰度也越高。各时间序列均呈现出明显的“尖峰厚尾”特征;同时,JB检验结果也表明各收益率序列与正态分布的假设不符,需采用学生t分布进行分析;Q检验结果证实部分收益序列波动的长期效应,ARCH检验也表明收益率序列存在明显的异方差;ADF的检验结果表明,除日价格外,各收益率序列在1%的置信水平下均为平稳序列。因此,下文可以采用GARCH类模型深入分析各收益率序列波动聚集情况。
四、实证分析
(一)协整检验
本文为进一步判断富时中国A50股指期货与股指现货价格序列之间是否存在长期稳定关系,由上文ADF平稳性检验结果可知LFt和LSt为一阶单整,下面采用协整检验对LFt和LSt之间短期与长期均衡关系进行检验。本文通过使用AIC、SIC、HQIC信息标准确定最优滞后阶数为17,并使用Johansen(1988)提出的MLE方法对VECM模型进行估计,运用VECM模型可以检验富时中国A50股指期货价格与现货价格的短期以及长期互动关系。Johansen协整检验结果如表2所示。
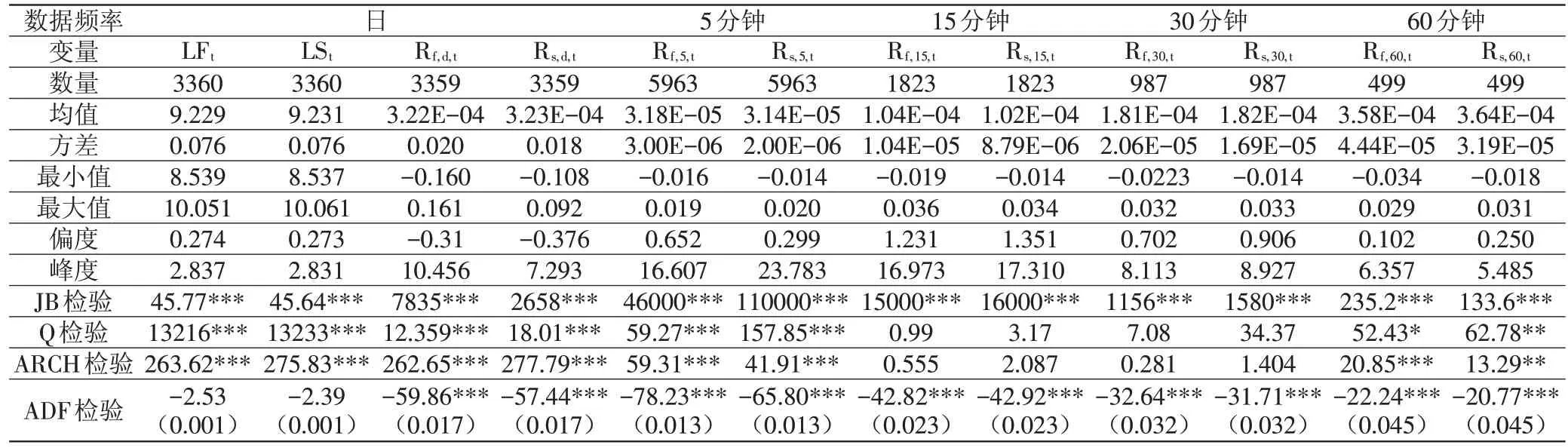
表1 各时间序列的描述性统计
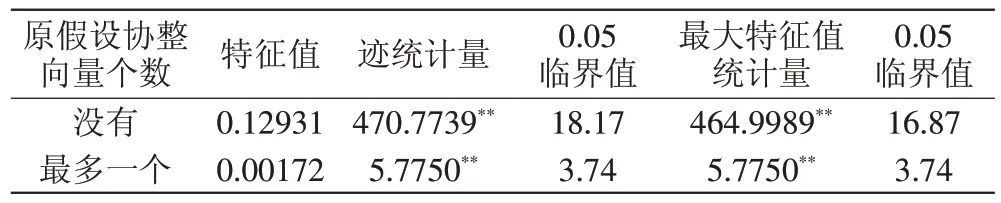
表2 Johansen协整检验结果
从表2的结果可以发现,特征根迹检验值和最大特征检验值都小于5%的置信水平下的临界值,由于是双变量,即富时中国A50股指期货价格与现货价格时间序列之间存在一个协整关系。基于VECM模型估计,可得出协整方程为:
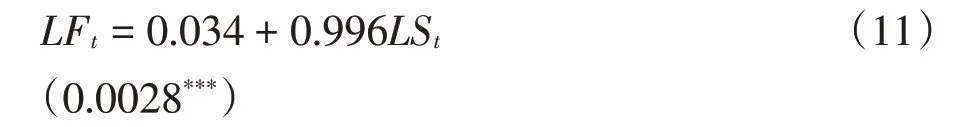
上式中的协整方程,协整系数(1,-0.996)近似(1,-1),这说明富时A50股指期货与股指现货之间存在长期均衡关系,同时具有较高价格发现效率。
(二)Granger因果检验
基于日价格序列,本文进一步检验不同时期富时中国A50股指期货与股指现货之间的价格引导关系,由于Granger因果检验只适用于平稳序列,而LFt与LSt为不平稳时间序列,无法进行Granger因果检验,因此需要采取其一阶差分序列Rf,t和Rs,t才具有解释意义。Granger因果检验结果如表3所示,在第四次股指期货政策“松绑”前,富时中国A50股指期货与股指现货价格存在双向引导关系;但第四次股指期货政策“松绑”后,在1%的显著性水平下,原假设——富时中国A50股指现货不是富时中国A50股指期货的Granger原因被拒绝,即说明富时中国A50股指现货引导股指期货走势。整体而言,成立至今,富时中国A50股指期货与股指现货价格走势密切相关,两者价格存在一种双向引导的关系。
(三)BEKK模型下的波动溢出效应检验
基于前文分析,富时中国A50股指期货与股指现货收益序列均呈现显著的ARCH效应。本文进一步采用二元的非对称BEKK-GARCH(1,1)模型探究富时中国A50股指期货与股指现货的波动溢出效应,实证结果如表4所示。
从对角元素α11、α22和b11、b22的估计结果来看,除5分钟和60分钟收益波动序列外,其余序列的扰动项系数α11和α22均在1%的显著性水平下显著,表明富时中国A50股指期货与股指现货收益率的波动序列存在ARCH效应。各波动序列中表示GARCH效应的b11和b22均在1%的显著性水平下高度显著,说明在短期内,富时中国A50股指期货市场与股指现货市场的当期收益率会持续受到自身前期波动的影响,前一期的波动会持续不断地影响本期的收益波动,可见各收益序列的波动具有较强的时变性和聚集性,富时中国A50股指期货市场具有一定的市场风险。
从非对角元素α12、α21和b12、b21的估计结果来看,各序列的参数估计都存在一定差异,15分钟波动序列的α12、α21分别在10%和1%水平下显著,这表明股指期货市场与股指现货市场都在相互作用和相互影响,两个市场具有双向的波动溢出效应。其中,5分钟波动序列的α12绝对值比α21绝对值大,说明股指现货市场对股指期货市场的冲击影响程度比股指期货市场对股指现货市场的冲击影响程度大。但30分钟与60分钟波动序列的α12=α21=b12=b21=0,说明股指期货市场与股指现货市场之间的波动互不影响。除30分钟与60分钟波动序列外,其余波动序列的b12、b21在1%或10%水平下显著,说明股指期货市场与股指现货市场都存在跨市场的波动持续性影响,其中5分钟波动序列、15分钟波动序列和日波动序列中b21>b12,反映出股指期货市场对股指现货市场的波动持续性影响程度比股指现货市场对股指期货市场的波动持续性影响程度大。15分钟与日波动序列的b12<0,表明股指现货的收益率波动对股指期货的收益率波动产生反向影响,两者关系在日波动序列中则相反。
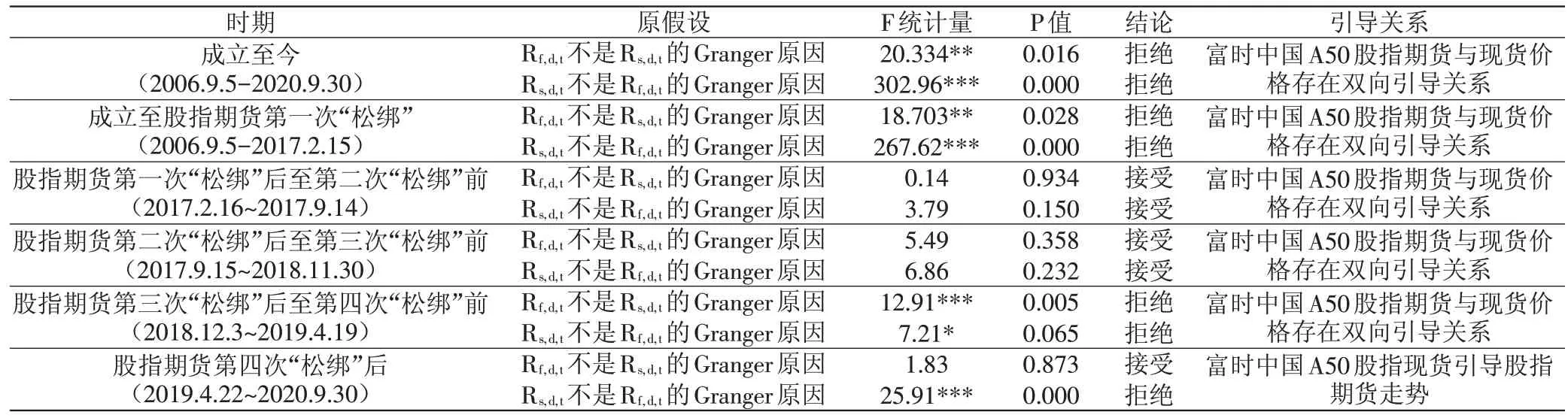
表3 富时中国A50股指期货与股指现货的Granger因果检验
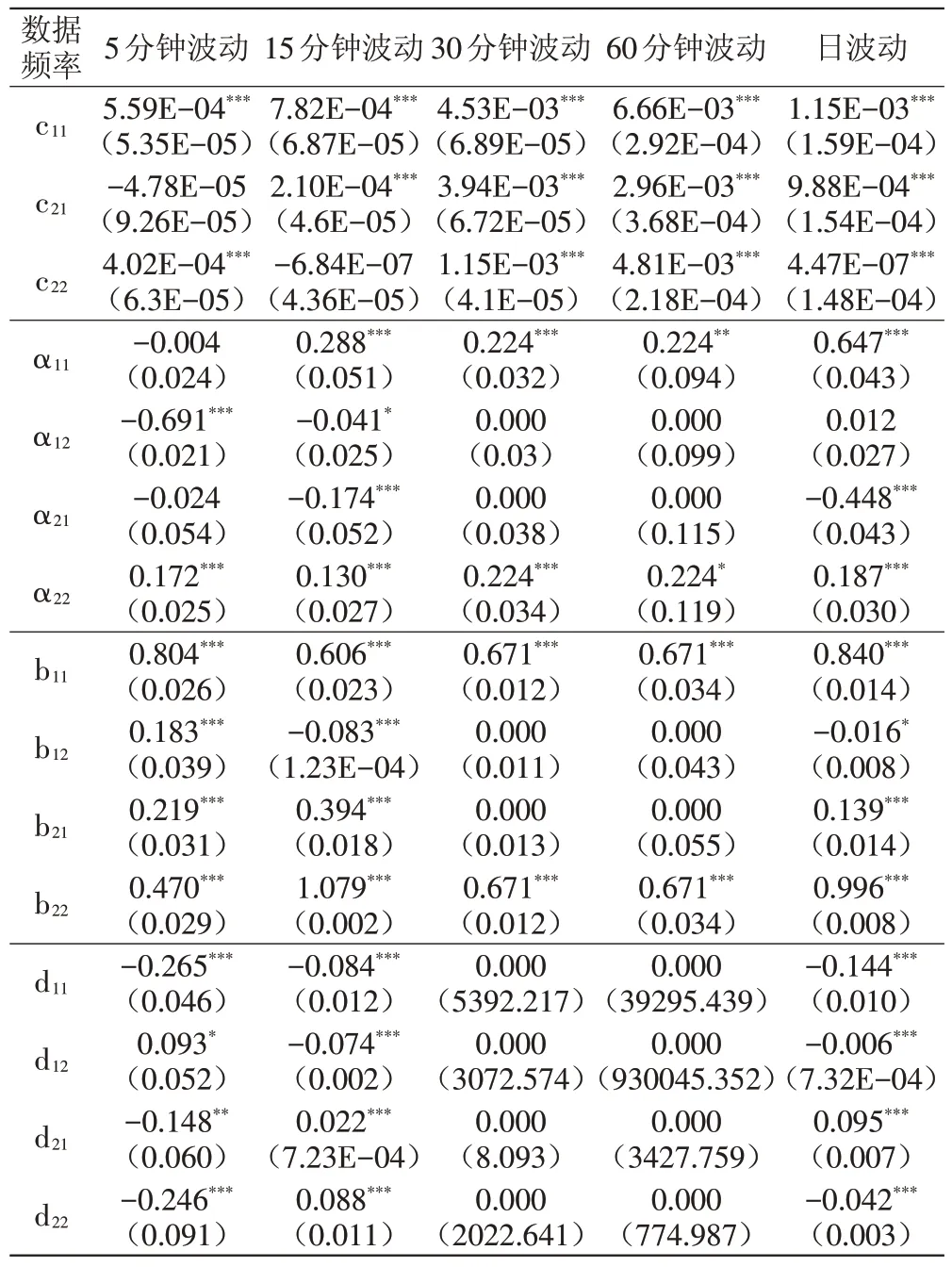
表4 波动溢出效应检验结果
从非对称效应的参数d11、d12、d21和d22的估计结果来看,5分钟波动、15分钟波动与日波动序列的大部分参数显著为负,说明股指期货市场和股指现货市场存在一方的坏消息都比好消息会造成更剧烈的波动,总体上看两个市场自身的非对称溢出效应比来自对方的非对称溢出效应更大。通过对比d12和d21的绝对值大小,可以发现5分钟与日收益波动序列中,股指现货市场对股指期货市场的非对称效应比股指期货市场对股指现货市场的非对称效应大;30分钟收益波动序列中d11=d12=d21=d22=0,说明股指期货市场与股指现货市场之间并不存在非对称效应。
总体而言,股指期货市场和股指现货市场均受到前期信息冲击,然而,不同频率的波动溢出效应存在一定差异,信息冲击产生双向波动溢出效应,随着波动频率变慢而显现一个“U”现象,即5分钟与日波动序列的双向波动溢出效应比30分钟波动序列强。除此之外,股指期货市场和股指现货市场也具有双向的波动持续性影响与非对称溢出效应,随着波动频率变慢都呈现一个“U”现象,说明随着收益序列波动频率拉长,富时中国A50股指期货与股指现货的溢出效应强弱也会发生变动,这表明波动溢出效应存在着明显的波动频率结构效应。
(四)DCC模型下的动态相关系数
本文进一步引入DCC-MVGARCH模型分析富时中国A50股指期货与股指现货之间的动态相关程度。结果如表5所示,在DCC模型估计结果中,回归结果均满足约束条件(λ1+λ2<1)。除60分钟波动序列的λ1不显著,其余各序列的参数估计量均在1%或10%水平下显著,λ1的估计系数相对较小,表明滞后一期的标准化残差乘积对富时中国A50股指期货与股指现货的动态相关系数影响非常小;λ2的估计系数均大于λ1,表明前期动态相关系数对当前动态相关系数具有较大的影响,说明富时中国A50股指期货与股指现货受到过去带来的冲击较大,且动态相关性的持续性较强;λ1+λ2的值随着数据频率变动而变化,反映出动态相关性的强弱呈现“U”趋势,说明动态相关性强弱具有时效性。
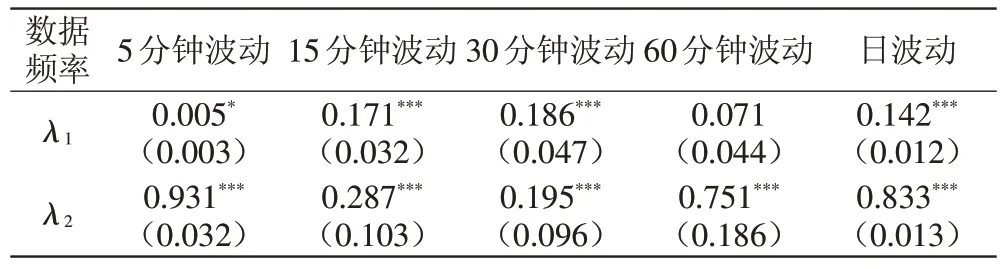
表5 DCC-MVGARCH模型部分参数估计结果
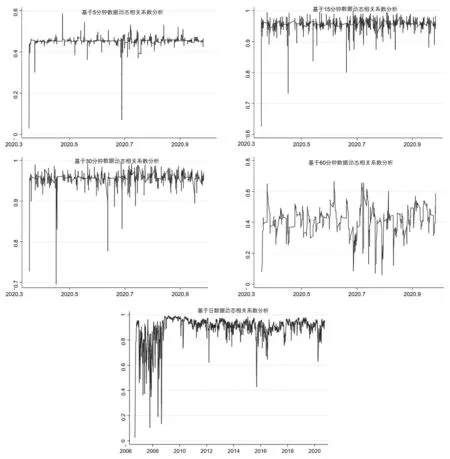
图2 动态相关系数的时序图
进一步观察富时中国A50股指期货对股指现货的态势变化,考察各时期动态相关系数变化过程。如图2所示,尽管富时中国A50股指期货与股指现货存在正相关关系,但是不同频率序列的动态相关性波动有所差异。从趋势上来看,随着数据频率变慢,股指期货和股指现货之间的波动变得剧烈。其中,15分钟与30分钟波动序列的相关性相对较高,均值分别为0.9561与0.9563,说明股指期货市场和股指现货市场的波动溢出效应较强;5分钟与60分钟波动序列的相关性相对较低,均值分别为0.4521与0.4116,说明股指期货市场和股指现货市场的波动溢出效应与其他频率序列相比较弱。整体而言,富时中国A50股指期货引导股指现货的波动,而动态相关系数的平稳性与数据频率息息相关,且数据频率越慢波动越剧烈,进一步说明两个市场之间联动存在时间效应,需要观察波动频率带来的影响。
五、结论
本文对富时中国A50股指期货与股指现货价格引导关系与波动溢出效应进行深入研究。实证研究显示:一是从价格引导关系上来看,富时中国A50股指期货与股指现货之间存在长期均衡关系,两者的价格走势高度一致,长期以来存在双向价格引导关系;二是从静态视角分析来看,利用非对称BEKKGARCH模型发现富时中国A50股指期货与股指现货的收益波动存在明显的波动集聚现象,并持续受到自身前期波动的影响,且两个市场之间相互冲击,存在双向的波动溢出效应,这些波动溢出效应和非对称溢出效应都存在明显的波动频率结构效应,即随着数据频率变化,溢出效应的强弱会发生一定变化,呈现“U”型变化趋势;三是从动态相关性来看,DCCMVGARCH模型结果显示两个市场存在强烈的持续性,且随着数据的频率不断变慢,动态相关系数波动越剧烈。因此,投资者可以通过富时中国A50股指期货判断其现货价格走势,但投资者需要关注价格的时间结构,不同波动频率内采用不同投资策略。

