欧拉函数方程φ(abc)=2(φ(a)+φ(b)+φ(c)-1)的正整数解*
郑 惠
(阿坝师范学院 数学学院, 四川 汶川 623000)
φ(n)是著名的Euler函数,它的值等于序列1,2,3,…,n-1中与n互素的整数的个数[1].包含Euler函数φ(n)的方程的可解性是初等数论中非常有意义的研究课题[2].Guy讨论了方程φ(x+y)=φ(x)+φ(y)的可解性[3];文献[4,5,6]分别研究了方程φ(n)=2ω(n),φ(φ(n))=2ω(n)及φ(φ(φ(n)))=2ω(n)的正整数解;文献[7~10]研究了方程φ(xy)=k(φ(x)+φ(y))的可解性;孙翠芳、王曦浛、张四保等分别讨论了k=2、3、4、5、6、7、8时,方程φ(abc)=k(φ(a)+φ(b)+φ(c))的可解性,并给出了方程的所有正整数解[11~17].本文将讨论方程φ(abc)=2(φ(a)+φ(b)+φ(c)-1)的整数解,并给出其所有正整数解,一共是34组.
1 主要引理

引理2[18]若n≥2是整数,则φ(n) 引理3[11]对任意正整数n,任意素数p,有 定理1 方程 φ(abc)=2(φ(a)+φ(b)+φ(c)-1) (1) 的所有正整数解为 (a,b,c)=(2,2,2);(1,4,4),(4,1,4),(4,4,1); (12,1,3),(12,3,1),(3,1,12),(3,12,1),(1,3,12),(1,12,3); (1,4,6),(1,6,4),(4,1,6),(4,6,1),(6,1,4),(6,4,1); (1,5,8),(1,8,5),(5,1,8),(5,8,1),(8,1,5),(8,5,1); (2,3,4),(2,4,3),(3,4,2),(3,2,4),(4,2,3),(4,3,2); (1,12,5),(1,5,12),(5,1,12) ,(12,1,5),(5,12,1), (12,5,1). 证明对于φ(abc)=2(φ(a)+φ(b)+φ(c)-1),根据引理1及欧拉函数的性质,有 即 φ(a)φ(b)φ(c)≤2(φ(a)+φ(b)+φ(c)-1), 从而有 φ(a)φ(b)φ(c)-2φ(a)=(φ(b)φ(c)-2)φ(a)≤2(φ(b)+φ(c)-1). (2) 下面根据φ(b)φ(c)的值的大小分两种情况加以讨论. (1)φ(b)φ(c)≤2. 此时,不等式(2)恒成立,且有 (b,c)=(1,1),(1,2),(2,1),(1,3),(2,2),(2,3),(1,4), (2,4),(1,6),(2,6),(3,1),(3,2),(4,1),(4,2),(6,1),(6,2). 当(b,c)=(1,1),(1,2),(2,1)时,将其带入式(1),显然方程无解. 当(b,c)=(1,3),(3,1)时,由引理3有 由此可得a=12,故此时方程(1)有正整数解(a,b,c)=(12,1,3),(12,3,1). 当(b,c)=(2,2)时,有 由此可知a=2,此时方程(1)有正整数解(a,b,c)=(2,2,2). 当(b,c)=(2,3)时,有 由此可得a=4,方程(1)有正整数解(a,b,c)=(4,2,3). 同理可得当(b,c)=(3,2)时,方程(1)有正整数解(a,b,c)=(4,3,2). 当(b,c)=(1,4)时,有 由此可得a=4,6,此时方程(1)有正整数解(a,b,c)=(4,1,4),(6,1,4). 同理可得当(b,c)=(4,1)时,方程(1)有正整数解(a,b,c)=(4,4,1),(6,4,1). 当(b,c)=(2,4)时,有 由此可得a=3,此时方程(1)有正整数解(a,b,c)=(3,2,4). 同理可得当(b,c)=(4,2)时,方程(1)有正整数解(a,b,c)=(3,4,2). 当(b,c)=(1,6)时,有 由此可得a=4,此时方程(1)有正整数解(a,b,c)=(4,1,6). 同理可得当(b,c)=(6,1)时,方程(1)有正整数解(a,b,c)=(4,6,1). 当(b,c)=(2,6)时,有 显然无整数使上式成立,故此时方程(1)无解. 同理可得当(b,c)=(6,2)时,方程(1)无解. (2)φ(b)φ(c)>2. 此时φ(b)φ(c)≥4,由φ(b)φ(c)+1≥φ(b)+φ(c)和式(2)可得 所以φ(a)=1,2,4. 当φ(a)=1时,式(2)为 φ(b)φ(c)=φ(a)φ(b)φ(c)≤φ(abc)=2(φ(b)+φ(c)), 从而 (φ(b)-2)(φ(c)-2)≤4. 当(φ(b)-2)(φ(c)-2)<0时,若φ(b)=1,则φ(c)>2,直接代入方程(1)验证可知方程无解.同理,若φ(b)>2,则φ(c)=1,方程(1)无解.从而 (φ(b)-2)(φ(c)-2)=0,1,2,3,4. 当(φ(b)-2)(φ(c)-2)=0时,有φ(b)=2,φ(c)>1或φ(b)>1,φ(c)=2,此时方程(1)有正整数解(a,b,c)=(2,3,4),(2,4,3),(1,4,6),(1,6,4),(1,4,4),(1,3,12),(1,12,3). 当(φ(b)-2)(φ(c)-2)=1时,有φ(b)=φ(c)=1,与φ(b)φ(c)>2矛盾.当(φ(b)-2)(φ(c)-2)=2,3时,由引理2知满足条件的φ(b),φ(c)的值不存在.当(φ(b)-2)(φ(c)-2)=4时,有φ(b)=φ(c)=4,此时方程(1)有正整数解(a,b,c)=(1,5,8),(1,8,5). 当φ(a)=2时,式(2)为 2φ(b)φ(c)=φ(a)φ(b)φ(c)≤φ(abc)=2(φ(b)+φ(c)+1). 于是 0≤(φ(b)-1)(φ(c)-1)≤2. 当(φ(b)-1)(φ(c)-1)=0时,有φ(b)=1,φ(c)>2或φ(b)>2,φ(c)=1,此时方程有正整数解(a,b,c)=(3,1,12),(3,12,1).当(φ(b)-1)(φ(c)-1)=1时,有φ(b)=φ(c)=2,直接代入方程(1)验证可知方程无解.当(φ(b)-1)(φ(c)-1)=2时,满足条件的φ(b),φ(c)的值不存在. 当φ(a)=4时,式(2)为 4φ(b)φ(c)=φ(a)φ(b)φ(c)≤φ(abc)=2(3+φ(b)+φ(c)). 于是 1≤(2φ(b)-1)(2φ(c)-1)≤7. 当(2φ(b)-1)(2φ(c)-1)=1时,有φ(b)=φ(c)=1,直接代入方程(1)验证可知方程无解.当(2φ(b)-1)(2φ(c)-1)=2,4,5,6时,满足条件的φ(b),φ(c)的值不存在.当(2φ(b)-1)(2φ(c)-1)=3时,有φ(b)=1,φ(c)=2或φ(b)=2,φ(c)=1,直接代入方程(1)得正整数解为(a,b,c)=(12,1,3),(12,3,1).当(2φ(b)-1)(2φ(c)-1)=7时,有φ(b)=1,φ(c)=4或φ(b)=4,φ(c)=1,此时方程(1)有正整数解(a,b,c)=(5,1,8),(5,8,1),(8,1,5),(8,5,1),(5,1,12),(12,1,5),(5,12,1),(12,5,1). 综上所述,得方程(1)的全部正整数解,一共是34组.证毕. 定理2 对任意的正整数k,(a,b,c)=(2k+1,2k+1,2k+1),(2k+1,3×2k,2k+1)是不定方程 φ(abc)=22k+1(φ(a)+φ(b)+φ(c)-2k) (3) 的正整数解. 证明由欧拉函数的定义知 φ(2k+1×2k+1×2k+1)=23k+2, 22k+1(φ(2k+1)+φ(2k+1)+φ(2k+1)-2k)=23k+2, 所以(a,b,c)=(2k+1,2k+1,2k+1)是不定方程(3)的正整数解.同理可证(2k+1,3×2k,2k+1)也是不定方程(3)的正整数解. 证毕. 本文讨论了当k=2,m=1时,方程φ(abc)=k(φ(a)+φ(b)+φ(c)-m)的可解性,并给出了方程所有正整数解.而对于其他的正整数k,m,效仿定理1中的讨论,同样可以得到相对应方程的解,只不过k,m变大时,可能计算量较大.
2 结果及其证明



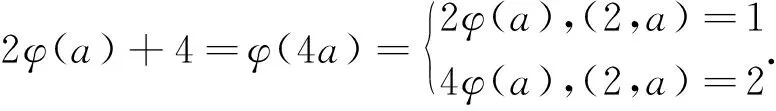



3 结论

