基于集合经验模式分解和样本熵的心脏猝死识别方法

石满红，武 柯,郭航志

(安徽科技学院 信息与网络工程学院，安徽 蚌埠 233030)

0 引言

心脏性猝死(Sudden cardiac death，SCD)是指一个人在出现症状后不到一小时内，因先前已知或未知的心脏疾病而突然死亡，尽管公共除颤设备的使用有所增加，但根据最新数据，由于未能及时为患者提供护理，只有大约10.4%的院外幸存者，伴有心力衰竭、冠状动脉疾病或心肌梗死病史的人患有SCD的风险更高[1].尽管SCD的主要原因还不清楚，心室颤动能够导致心脏泵血功能衰竭进而导致死亡，它被认为是20%的SCD的潜在发作机制，且患者的存活率在经历过心室颤动以后每分钟下降10%[2].故对于经历过心室颤动的人来说，早期发现未预料到的 SCD 对于提高 SCD 风险患者，尤其院外患者的生存率非常重要.

HRV已被证明是心肌梗死后死亡的一个独立指标[3].HRV信号的分析方法主要有经典线性方法(包括时域、频域)、时频和非线性方法3种.Van Hoogenhuyze等人在1989年的一项研究报道表明，与正常组相比，SCD组中HRV的平均窦房结R-R间期(SDANN)、标准差的均值的统计特征较低.除了上述对HRV信号进行时域分析外，Shen等人还对HRV信号进行了快速傅里叶变换(FFT)来获取频域特征，发现各种标准片段(比如高频(HF)、低频(LF)和甚低频(VLF))是SCD的强指标[4].在时频域，对HRV信号进行Wigner-Ville变换、平滑pseudo Wigner-Ville分布和短时傅里叶变换，得到相应的时频特征，用于SCD预测[5-7].有研究表明，与经典的HRV信号分析方法相比，由于HRV信号本身的非平稳和非线性特性，非线性分析方法如重整熵、条件熵、相互非线性预测和符号动力学等，能更好地挖掘信号内部包含的复杂性[8].此外，Ebrahimzadeh等人在对HRV信号分析中，较之经典的线性分析，非线性特征在区分SCD受试者与正常受试者方面的表现更加稳定[9].样本熵(SamEn)作为典型的信号非线性分析方法被广泛应用于许多信号和图像处理应用[10-11].Fujita等人提出结合非线性特征(Renyi熵，模糊熵，Hjorth’s参数，Tsallis 熵)和小波变换的算法，对HRV信号进行处理，能够在SCD发生前4 min进行预测[12]，然而，由于小波分解对于信号的分解不具有自适应能力，选择合适的基函数对于信号分析至关重要.集成经验模态分解(EEMD)是不需先验知识,只有根据信号本身特点的自适应信号分解方法,将信号分解成固有模式函数,这对于非线性和非平稳信号的分析极其重要[13].EEMD信号分解方法已经在各种信号的分析中显示出其优越能力，如心电图心跳的分类[14]，可电击性室性心律失常的检测[15]，以及充血性心力衰竭的自动识别[16].因此，结合样本熵与集合经验模式分解的优势，提出基于集合经验模式分解的样本熵应用于心脏猝死早期识别.

1 数据与方法

1.1 信号获取

以PhysioBank miti-BIH Normal Sinus Rhythm(NSR)和MIT/BIH SCD作为评估数据.在23例SCD患者中，仅选取20例(8例女性，10例男性，2例未知，年龄18～89岁)进行进一步分析，因为其他3例患者的心电信号未出现任何VF发作.从SCD数据库中总共使用了来自MIT-BIH NSR的36条心电图记录和来自SCD数据库的40条SCD心电信号.为了在正常组和SCD风险受试者之间保持一致的采样，使用的所有心电图信号重新采样至360 Hz.在SCD患者24 h心电记录中，仅使用VF发作前5 min心电信号，以此模拟SCD前5 min.对于正常受试者，随机选择5 min心电信号.心电信号在采集过程中会受基线漂移(<0.5 Hz)、电源线干扰(>50 Hz)等各种噪声干扰[17]，采用小波基为Daubechies 6阶的DWT对获取的ECG信号进行分解，此方法适用于非平稳信号的分解[18],将分解得到的前两个细节系数和最高近似系数设置为零，用于心电信号去噪，然后对去噪后的心电信号采用Pan Tompkins算法，检测QRS波，确定相应的HRV信号.HRV信号分析前需要对HRV信号进行预处理，因为缺失的或是错误的R峰会带来异位间隔，从而产生差质量的HRV信号.采用中值滤波器方法删除超过对后5个和前5个RR间隔的中值 20% 的RR间隔的方法[19]，来对HRV信号进行预处理.

1.2 经验模式分解(Empirical Mode Decomposition,EMD)

在给定信号x(n)的情况下，EMD的出发点是识别所有的局部最大值与最小值，以上包络eu(n)的三次样条曲线连接所有这些最大值.同样，所有局部极小值都用样条曲线作为下包络e1(n)连接，两个包络的均值表示为：

m1(n)=[eu(n)+el(n)]/2.

(1)

因此，第一个成分h1(n)可由式(2)获得：

x(n)-m1(n)=h1(n).

(2)

上述提取的固态莫函数(IMF)的程序称之为筛选过程，理想情况下当h1(n)满足IMF的两个要求时，h1(n)即为IMF.由于h1(n)在过零点之间仍然包含多重极值，因此在h1(n)上再次执行筛选过程，该过程经反复应用，得到满足IMF条件的第一个IMFc1(n).接着使用两个停止准则来终止筛选过程，最常用的标准是标准差(Standard Deviation，SD)，它是从两个连续的筛选过程中计算出来的：

(3)

这里的N代表信号x(n)中样本点的个数，当SD小于给定的阈值时，得到第一个IMF.那么c1(n)由式(4)从剩下的数据中分离出来:

x(n)-c1(n)=r1(n).

(4)

需要注意的是，残差r1(n)包含一些有用的信息，因此，将残差作为信号，采用相同的筛选过程获得

ri-1(n)-ci(n)=ri(n),i=1,…,q.

(5)

当分量cq(n)或是rq(n)变小或残差rq(n)变为单调函数时，整个过程结束.结合式(4)、(5)产生原始信号的经验模式分解：

(6)

分解得到q个固态模函数和一个残差，低阶IMF捕获快速震荡模式，高阶IMF代表缓慢震荡模式[13].

1.3 集合经验模式分解(Ensemble Empirical Mode Decomposition ,EEMD)

在EMD方法中,存在模态混合现象与端点效应，造成模态混合现象的主要原因是震荡信号中混有脉冲、间歇性以及噪声等信号，这些信号使得信号的分解层数增加，相应的时效性降低，甚至出现非常严重的模态混叠的现象.为了解决EMD方法的局限性，Wu 和 Huang[13]在2009年提出了一种改进的EMD信号分解方法—集合经验模式分解(EEMD)，通过加入有限幅值的高斯白噪声均匀分布在整个时频空间，加入白噪声分量将原始信号的各个尺度分量映射到合适的参考尺度上.因被分解的信号由白噪声和原信号构成，使得每一次分解试验的结果都是有噪声的.但通过计算所有试验的总体均值，完全消除了均匀分布的白噪声，通过这种方法，有效地避免了EMD的模态混合现象[15].EEMD算法过程表述如下:

步骤1 加入不同标准差的高斯白噪声(ni(t),i=0,…,L)到原始信号x(t)：

xi(t)=x(t)+ni(t).

(7)

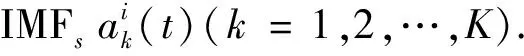
步骤3 计算集合信号xi(t)的第k个IMF：

(8)

利用EEMD(D=0.2)将5 min HRV信号分割成多个IMF，然后提取相应的特征.考虑到重建误差的可容忍程度，都使用了前4个IMFs.图1描述了SCD发生前5 min间隔HRV信号的分解.

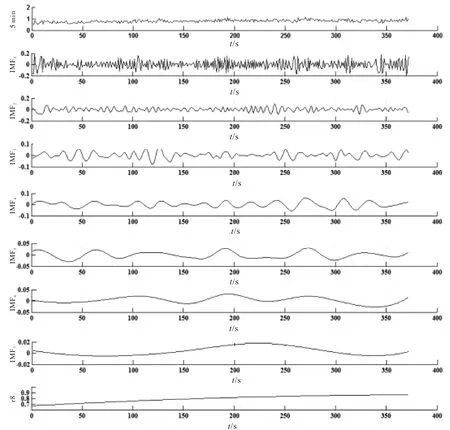
图1 利用EEMD技术对SCD发生前5 min HRV信号的分解

1.4 样本熵

样本熵(sample entropy,SamEn)测量生理信号的规律性，与模式长度无关.对于给定模式长度(m)和相似度准则(r)，如果一个数据集的样本熵值高于另一个数据集，那么对于所有不同的模式长度(m)和相似度准则(r),SamEn值都高于另一个数据集.因此，SamEn相对一致且减少了近似熵的偏差.较高的SamEn值表示该信号是高度不可预测的，较低的SamEn值表示该信号是可预测的.SamEn的计算过程如下：

1)对于时间序列{μ(i),i=1,…,N}，构造m维向量：

Xi={u(i),u(i+1),…,

u(i+m-1)},1≤i≤N-m+1.

(9)

2)定义向量Xi和Xj的最大距离函数d[Xi,Xj]，记Nm(i)为满足d[Xi,Xj]≤r条件的个数.

3)计算

(10)

其中：i=1,…,N-m+1.

4)构造m+1维向量，重复上述步骤，类似地计算Bm+1(r).

5)SamEn为:

(11)

这种熵的优点是:(i)它可以用于短序列的有噪声数据;(ii)它能够区分不同的复杂度信号;(iii)对于随机数，它比近似熵度量更准确;(iv)它保持了相对一致性.根据以往的研究经验，这里SamEn的n=2，r=0.15*SD(SD 表示时间序列的标准差)，m=2[10].

1.5 分类能力评估方法

为了确定所获得特征的统计意义和分类性能，采用了包括t检验的统计分析方法.当t检验生成的特征的p值小于0.05时，该特征被视为统计显著性，p值越小，对应统计显著性越明显.此外，为了区分SCD和正常人，SVM分类器中采用不同的核函数，且分别计算3个评估指标(准确度、灵敏度和特异性)，以评估分类器的性能.为确保分类结果的公正性和可信性，实施了5倍交叉验证方法，并计算了总体评估指标.

2 结果

表1显示的是样本熵与集合经验模式分解第一层分解的固态模函数的样本熵的平均值和标准差，从表1不难看出，直接计算不同群体的心率变异性信号的样本熵的值，在正常人与心脏猝死患者之间不具备差异性(p=0.683)，而将集合经验模式分解作用于心率变异性信号，计算分解获得的第一层固态模函数的样本熵的值，在两者之间存在显著性差异(p=2.91e-9)，图2显示的是样本熵(SamEn)与基于集合经验模式分解的样本熵(EEMD-SamEn)的值在正常人与SCD患者之间的箱线图，不难发现，EEMD-SamEn在正常人与SCD患者之间具有显著性分离，区分性能好.

表1 正常人与CHF HRV信号的SamEn和EEMD-SamEn对应的p值

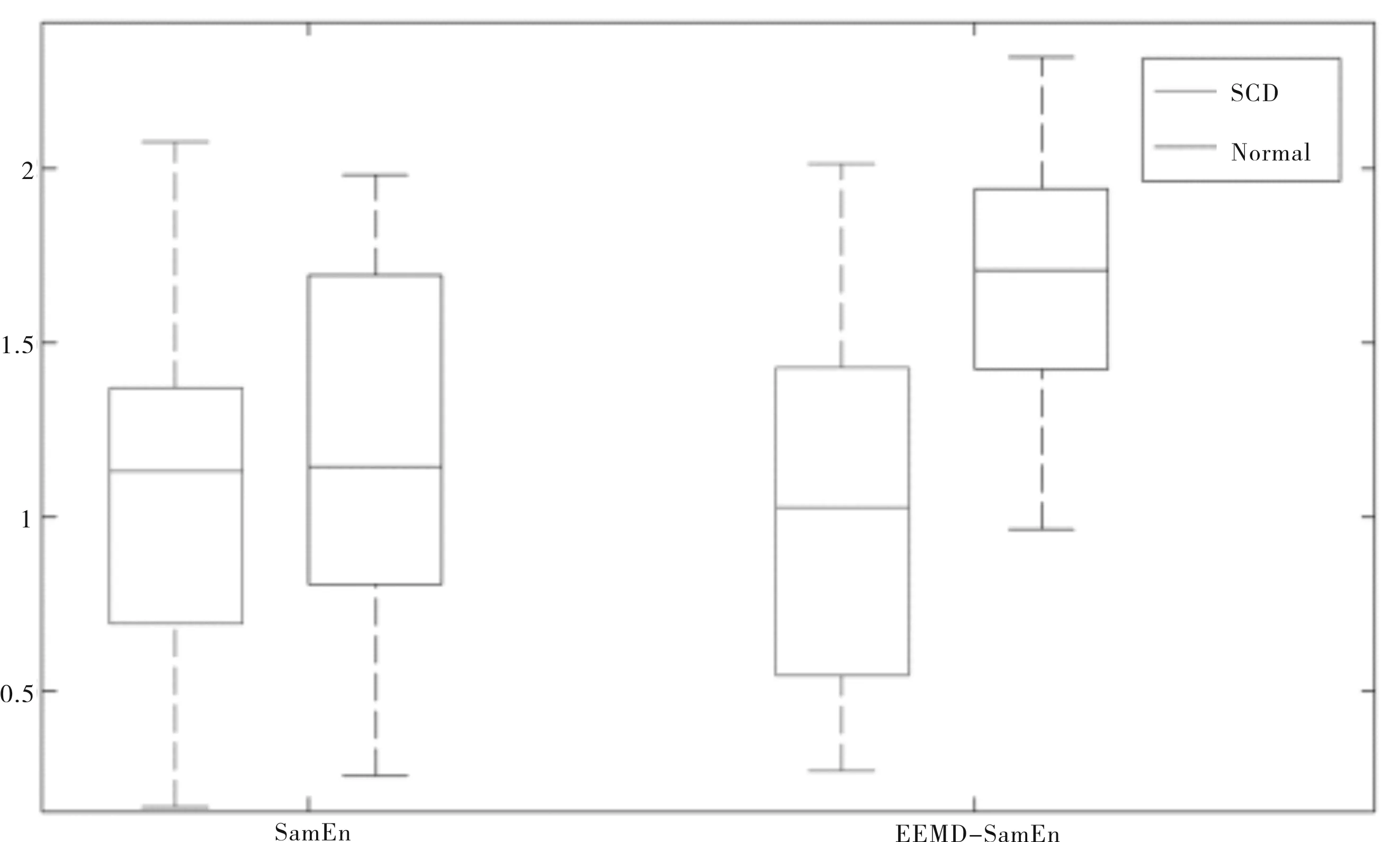
图2 样本熵与基于集合经验模式分解的样本熵在不同群体间的箱线图

随后，分别将SamEn与EEMD-SamEn输入不同核函数的SVM分类器，表2显示的是分类结果，由表2不难看出，EEMD-SamEn在使用核函数为Quadratic和Gaussian都获得80.3%的准确度，而SamEn获得的准确度分别为47.7%和53.9%，且EEMD-SamEn获得的平均准确度、灵敏度、特异性分别为75.03%、68.13%与80.38%.显著高于SamEn.

表2 使用不同核函数的SVM分类器的分类性能 %

3 结论

研究表明，全世界每年都有数百万人由于SCD丧生，因此，急需一种合适的方法来提前识别SCD，尽可能早地发出预警信息，以便医生可以为有风险的患者做出及时的后续治疗.笔者基于集合经验模式分解与样本熵提出基于集合经验模式分解的样本熵应用于SCD患者的识别，数值实验基于集合经验模式分解的样本熵达到80.3%，它对SCD风险患者的识别具有较高的实用价值.