一类随机泛函微分方程的双加权伪概周期解
朱 平
(洛阳师范学院 数学科学学院,河南 洛阳 471934)
0 引言
自Bohr提出概周期函数以来,其一系列推广的研究已引起越来越多的关注.作为概周期函数的推广之一,双加权伪概周期函数于2011年由Diagana提出[1],并应用到一类微分方程的双加权伪概周期温和解的研究中.近年来,双加权情形虽然也逐步推广并丰富了随机过程的动力学行为,但研究成果甚少,尤其是对泛函微分方程[2-4].到目前为止,p次双加权伪概周期随机过程尚未研究,因此笔者对如下一类由G-Brown运动驱动的非自治随机泛函微分方程
(1)
在合适的条件下,证明该随机微分方程存在唯一双加权伪概周期温和解.该结论的研究进一步丰富了概周期随机过程的复杂动力学,因此笔者的研究内容具有重要的理论意义.
1 基本知识
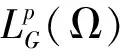

下面,介绍一些新定义和引理.


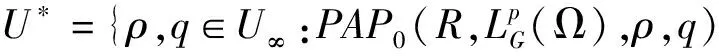
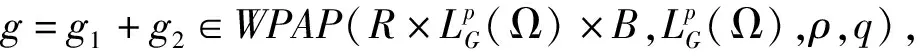
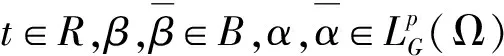
2 存在唯一性
为证明本节的主要结论,需做以下假设.
(H1)存在常数K>0和δ>0,当t≥s时满足
‖T(t-s)‖≤Ke-δ(t-s).
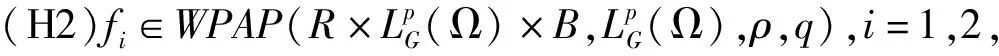
定义3 如果
称随机过程x(t)是随机微分方程(1)的温和解.
定理1 令ρ,q∈U*且(H1)-(H2)成立,若
(2)
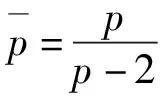
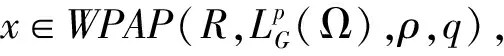


fi(t,x(t),xt)=gi(t,y(t),yt)+fi(t,x(t),xt)-fi(t,y(t),yt)+hi(t,y(t),yt),


其中:
下面,分两步进行证明.


E‖h2(s,y(s),ys)‖p)dsq(t)dt≤
E‖h2(s,y(s),ys)‖p]dsq(t)dt≤
E‖h2(t-s,x(t-s),xt-s)‖p]q(t)dtds,
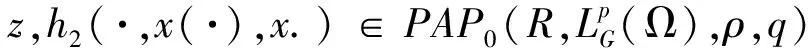
利用Lebesgue控制收敛定理,则有


第二步.算子Г是压缩映射.
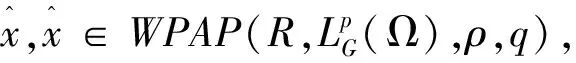
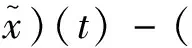
利用(2),则
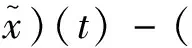
综上所述,利用Banach不动点定理可得随机微分方程(1)存在唯一的双加权伪概周期温和解.
3 结论
首先,在Banach空间中提出p次双加权伪概周期随机过程的定义,并给出相应的复合定理;其次,对一类由G-Brown运动驱动的非线性随机泛函微分方程,根据所得的复合定理,借助算子半群理论、Hölder不等式、Burkholder-Davis-Gundy不等式、Lebesgue控制收敛定理、Fubini定理等分析方法和分析技巧,利用Banach不动点定理证明该类随机泛函微分方程存在唯一的p次双加权伪概周期温和解;最后,该结论在已有研究中并未涉及,因此具有一定的创新性.

