卫星斜装成像载荷目标可见性分析方法

张淳 刘鹤 赵阳 韩小军

(北京空间飞行器总体设计部，北京 100094)

世界范围内的航天机构都在积极开展空间监视技术研究，通过维护和整合空间监视和情报信息，发展准确、及时的空间态势感知能力[1-2]。从20世纪90年代到21世纪初，美国实施了多项空间目标监视卫星技术试验项目，包括“中段空间试验卫星”(MSX)、试验卫星系统-10和11(XSS-10和11)、微卫星技术试验-A和B(MiTEx-A和B)、低轨天基空间监视系统-1(SBSS-1)、高轨“地球同步轨道空间态势感知计划”(GSSAP)、高轨“评估局部空间自主守卫纳卫星”(ANGELS)、低轨“可操作精化星历表天基望远镜”(STARE)卫星[3]。

空间态势感知网是空间监视发展的必然趋势，利用天基监视系统中的成像载荷实现空间目标的跟踪和定轨。针对空间态势感知和地面观测预警任务，基于成像载荷的空间和地面目标可见性分析是监视预警系统设计和验证的关键问题之一，有相当数量的文献对不同任务情景下的可见性计算问题进行了分析和讨论[4-8]。上述工作中均假设卫星为质点，或姿态已知确定，此时可以根据卫星与目标的相对位置和姿态，解算出卫星目标连线与视轴夹角，或与视场区域的位置关系，从而判断出目标是否可见。实际中，监视卫星通常具有某些方向上的姿态机动约束，成像载荷也存在斜装的可能，而已有的方法难以处理此类情况，或无法获取准确结果。另外，姿态机动约束、成像载荷斜装下的可见性计算未见有公开文献讨论，在STK软件中也不支持此类情景下的分析计算。

为克服上述问题，支撑工程分析应用，本文提出一种适用于姿态机动约束、成像载荷斜装的目标可见性分析方法。该方法适用多种应用场景，采用纯解析方式计算，无需迭代和优化，无数值多解、奇异等计算稳定性问题，因此准确性和效率较高。

1 可见性分析方法架构

本文坐标系定义如图1所示。轨道坐标系以OOXOYOZO表示，原点位于卫星质心OO，ZO轴指向地心，YO轴与轨道面垂直，XO轴与YO，ZO轴构成右手坐标系，指向飞行方向。卫星本体坐标系以OBXBYBZB表示，XB，YB，ZB轴分别与卫星主惯量轴重合，依照“321”转序由轨道坐标系变换得到。成像载荷坐标系以OCXCYCZC表示，ZC轴沿视轴指向被观测方向，XC轴和YC轴分别与成像载荷视场的对称轴方向重合。

(1)

q=q1∘q2=

(2)

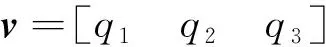
(3)

可见性分析需要考虑计算的效率、观测模式的适用性及多种约束下解的正确性。通常，可见性预报是逐个轨道位置计算对目标的可见性，再合并结果形成可见性窗口；然而，这种方式计算效率较低，需要引入自适应机制来提高整体分析过程的效率。另外，成像模式对可见性计算过程影响较大，有必要对成像模式进行规范化，增强后续可见性分析过程对各类成像模式的适用性。最后，如何在成像载荷斜装和姿态机动约束条件下正确求解可见性，是需要重点考虑的问题。

针对上述问题，本文提出一种具有通用性的可见性分析架构，主要过程包括预报步长自适应、成像模式规范化、几何可见性预判、无约束理想姿态计算、有约束接近姿态计算、视场下目标落位判断和可见区间精化。首先，根据监视卫星与目标的位置关系，以卫星对目标角度分辨率或卫星轨道周期为基准，自适应调整可见性计算的步长，假设相同可见性计算结果的临近区间内具有一致的可见性，获得初步可见性窗口。在此基础上，将可见区间的首末位置以二分法进行区间扩展，形成精化的可见性区间，在保证分析精度的情况下实现计算效率的提高。限于篇幅，预报步长自适应和可见区间精化均不再赘述，可见区间精化可参考文献[10]。成像模式规范化是对输入进行适配，以消除不同卫星成像模式的计算差异性，增强方法通用性。几何可见性预判主要以监视卫星和目标的相对位置关系为基础，通过几何角度约束快速剔除不可见轨道位置，相关方法与文献[6-7]所述方法相似，本文不再赘述。无约束理想姿态计算过程是指获取成像载荷斜装条件下视轴对准目标时所需要的理想卫星姿态。在此基础上，有约束接近姿态计算过程判断当前姿态约束下是否能够实现上述姿态，并在理想姿态不满足约束时，计算约束条件下视轴最接近目标方向时的接近姿态。最后，视场下目标落位判断过程计算上述接近姿态下目标是否处于成像载荷视场范围内。通过几何可见性预判、无约束理想姿态计算、有约束接近姿态计算、视场下目标落位判断等计算过程，可在目标可视仰角约束、监视卫星姿态约束、成像载荷安装矩阵约束、成像载荷视场形状和参数等约束下确定任意时刻成像卫星对目标的可见性。需要补充说明的是，卫星姿态约束可能需要处理不连续的姿态机动区间，成像载荷斜装则指成像载荷坐标系与卫星本体坐标系在多个轴上存在转动偏离，如图1中的允许姿态机动范围区间φ1，φ2及成像载荷坐标系所示。下面各节分别对上述主要过程进行分析。

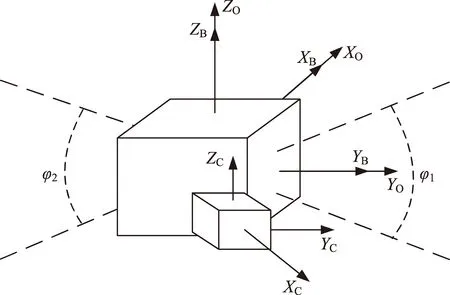
图1 分段姿态约束与成像载荷斜装示意Fig.1 Illustration of slant-mounted imaging payload and attitude constraints

2 成像模式规范化

针对空间和地面目标监视任务，观测模式的多样性会对目标可见性计算带来影响。成像模式规范化根据成像模式对可见性分析的输入进行处理，使后续可见性分析过程具有通用性，适用于各类目标的监视。光学成像载荷的成像模式包括扫描、凝视等，微波成像载荷的成像模式包括聚束、条带、滑动聚束等[11-12]。对于光学成像载荷的凝视模式和微波成像载荷的聚束模式，成像载荷始终聚焦于目标。对于光学成像载荷的扫描模式和微波成像载荷的条带模式，卫星以固定姿态获取成像载荷覆盖区域的图像信息。对于微波成像载荷的滑动聚束模式，微波成像载荷覆盖目标，但视场于一定周期内划过目标，形成对目标的积分成像效果。图2为3种成像模式的区别，t为目标，T为成像载荷的实际聚焦中心。

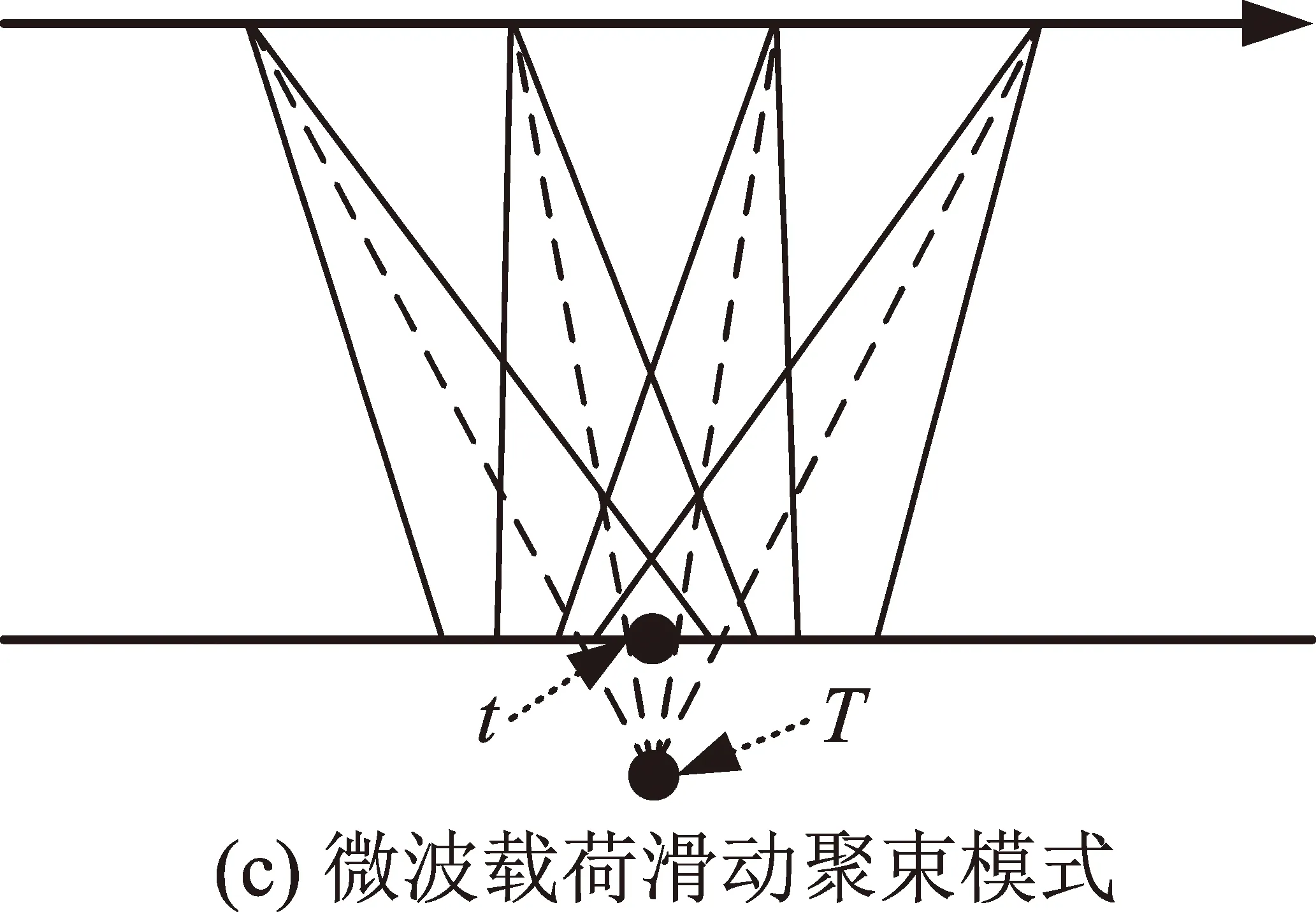
图2 成像模式示意Fig.2 Illustration of observation modes

(1)对于光学成像载荷的凝视模式和微波成像载荷的聚束模式，期望成像载荷视轴始终对准目标，当视轴受约束无法对准目标时，则尽量使视场能够覆盖目标。此种模式下，无需采用确定性姿态，无需对目标位置信息进行处理。

(2)对于光学成像载荷的扫描模式和微波成像载荷的条带模式，期望以确定姿态对成像载荷视场内区域进行观测，此时设置确定性姿态，无需对目标位置信息进行处理。

(3)对于微波成像载荷的滑动聚束模式，需要根据实际目标位置计算成像载荷聚焦中心位置。设卫星位置为PS，实际目标位置为Pt，则目标相对卫星位置为Pt,S=Pt-PS，设成像载荷对目标的积分比例因子为f，则成像载荷聚焦中心相对卫星的位置为PT,S=(1+f)Pt,S，进一步得聚焦中心位置为

PT=PS+PT,S=PS+(1+f)(Pt-PS)

(4)

3 无约束理想姿态计算

为最终确定姿态约束下监视卫星对目标是否可见，需要确认成像载荷斜装条件下卫星的理想成像姿态，为进一步检验姿态约束的满足情况提供基础。

(5)

(6)

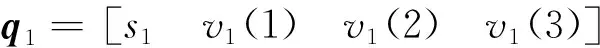
(7)

为避免数值求解上述非线性方程组可能带来的计算效率和数值稳定性问题，采用解析方式进行处理。易知上述四元齐次方程基础解为

(8)

式中：xi为基础解；ki为待定系数。

xi与ki的数量取决于q1和q2所组成矩阵的秩条件，考虑到方程组数量，xi与ki的数量个数至多为4。假设其数量为nxi，需要针对nxi不同取值分别进行讨论。

(1)当nxi=1时，将单位四元数约束代入基础解，可得

(9)

(2)当nxi=2时，将偏航指向约束方程与基础解联立，将单位四元数约束方程与基础解联立，可得式(10)～(12)。进一步对c1是否为零，以及k1与k2的正负性进行讨论，可获得具体解。最终，将有4种k1，k2组合解，根据式(7)引入约束sr2+vr2(1)-vr2(2)-vr2(3)>0，可确定具体解值。

c1k12+c2k1k2+c3k22=0

(10)

c4k12+c5k1k2+c6k22=1

(11)

(12)

(3)当nxi>2时，引入公共系数和公共基础解，令k2′=k2=k3=…及x2′=x2+x3+…，获得式(13)形式的解结构。然后,采用与上述nxi=2同样的计算过程即可。

(13)

4 有约束接近姿态计算

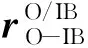
p=arctan(x/z)

(14)

r=arctan(-y/z)

(15)

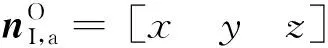
获得理想姿态对应的俯仰角p和滚动角r后，判断其是否处于允许的姿态范围内。根据假设，输入的姿态约束定义在非欧拉角意义下的俯仰角和滚动角，因此可直接进行比对。对于部分卫星和任务，姿态角约束区间并不一定连续，可能存在多段范围，此时需要逐个区间进行边界检查。

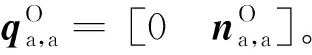
(16)

(17)

5 视场下目标落位判断

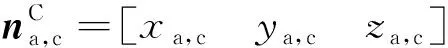
图3 落位判断示意Fig.3 Illustration of field sector determination

6 仿真验证

本节通过仿真验证所提方法的正确性，将可见窗口的起始时刻和结束时刻计算结果与STK软件仿真结果作比较。其中，仿真参数设置如表1所示。为简化仿真，选择固定目标；为提升验证效果，选择具有极小视场张角的矩形视场范围。

表1 仿真参数Table 1 Simulation parameters

(1)在不考虑姿态角约束的情况下进行仿真，得到如表2所示对比结果。如前所述，可见性的计算需要以卫星、目标位置等信息为输入，为保持输入的一致性，本文方法在每一步计算过程中均使用了STK软件提供的位置信息，以排除轨道外推时模型和系数组差异所引入的误差。受条件所限，STK软件输出的位置信息步长设为10 ms，因此本文可见性分析结果保留到10毫秒级精度，并未采用内插等方式进一步提高分辨率。通过比较，本文方法与STK软件可见性分析结果存在30 ms左右的差距，可知在STK软件可仿真的无姿态约束情景下，本文方法能够正确获得可见性预报结果，同时具有一定的计算精度。

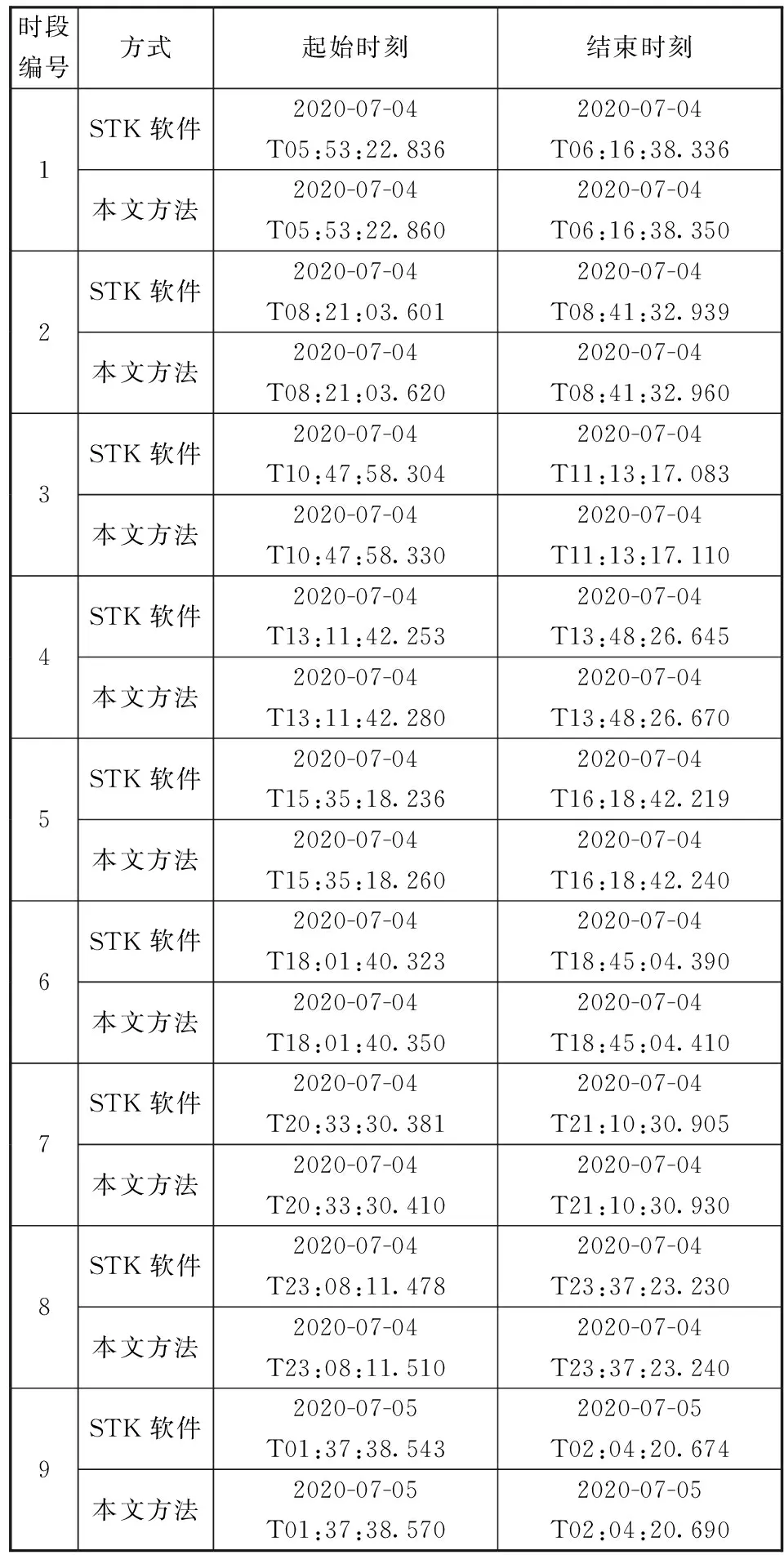
表2 无姿态约束下的可见性仿真结果Table 2 Visibility simulation results without attitude constraints

(2)增加滚动角方向上的双侧约束，该条件下计算结果如表3所示。这里将设置姿态约束前后的结果进行比对，可以看出：由于姿态约束的作用，可见性区段出现了明显的时段缩减(如表3中加粗项所示)。其中：约束前3号时段在约束后出现了可见性中断；约束前6号时段在约束后已不可见，检查约束前6号时段STK软件凝视目标时的卫星姿态，确认超出约束后滚动角机动范围，可间接验证本文方法的正确性。目前，STK软件无法支持类似本文仿真算例中的计算分析，因此本文方法对姿态约束、成像载荷斜装条件下考虑视场范围的可见性分析计算问题提供了有效支撑，特别适用于存在一定机动能力和视场监视范围卫星的可见性分析和预报。相比传统方法中视轴完全对准或固定姿态扫描目标等条件下获取的保守可见性窗口，本文方法有助于进一步挖掘系统能力，提升任务效能。

表3 姿态约束下的可见性仿真结果Table 3 Visibility simulation results with attitude constraints

7 结束语

本文针对空间态势感知和地面观测预警任务，面向配置有成像载荷的卫星，提出了一种解析化的可见性分析方法，可实现多段观测姿态约束、成像载荷斜装、视场范围约束等条件下的可见性分析，并通过仿真分析验证了所提方法的正确性和有效性。可见性快速分析主要服务于各类任务规划应用，为建立通用化的任务规划系统架构、增强各层级算法对多卫星的适用性铺垫基础，后续可进一步开展自治性星群的智能规划技术研究。