高中生数学核心素养评价问卷的编制

摘   要

问卷编制是数学核心素养评价的重点，通过构建数学核心素养评价框架和编制问卷，并进行预调查问卷的分析与修订、信效度检验，最终正式建立评价问卷。将数学核心素养评价指标确定为6个一级指标、14个二级指标。评价维度确定为數学内容、评价指标、水平、情境、问题类型。评价题型确定为选择题、填空题、判断题、解答题、开放型建构题5类。通过实证研究，该问卷能对高中生数学核心素养水平及等级进行有效评价。

关键词

高中生  数学  核心素养  评价问卷

数学核心素养作为一种具有数学特征的必备品格与关键能力，对个人和社会发展起到了横向连通、纵向贯通的作用。《普通高中数学课程标准（2017年版）》[1]提出的数学学业质量标准，为数学核心素养的评价提供了理论依据[1]。评价是为了寻找实际结果与课程目标的差异[2]，数学核心素养的评价，旨在了解学生数学核心素养的水平如何，存在哪些不足，通过哪些培养策略能够得到提高等。自2015年以来，数学核心素养的研究逐步系统、规范，在教育研究、学校课程和学校教学等方面形成了系列研究成果，但数学核心素养的评价研究相对缺乏，也需要通过实证研究对评价问卷的效度进行检验和说明。为此，研究者尝试以高中生为研究对象，在已有研究的基础上，开发高中生数学核心素养评价问卷，为进一步深入研究提供基础。

一、数学核心素养评价框架的建构

1.概念界定

数学核心素养可以理解为：学生应具备的适应终身发展和社会发展需要的、与数学相关的必备品格和关键能力。其核心要点为：学生学习数学之后形成的、具有数学学科特点的关键成就，是数学学科育人价值的集中体现;学生进行数学学习所必须具备的基本专业素质，其以内隐、稳定的方式存在于主体之中，是数学基础知识、基本技能、基本经验、基本思维品质、基本态度、价值观的有机融合。数学核心素养概念的界定，有利于进一步明确数学核心素养评价的目标，也便于分解评价指标。

2.评价指标的确定

在研究中，将数学核心素养的评价确定在6个一级指标（数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析），14个二级指标（数学表征、抽象思考;合情推理、演绎推理;问题提出、模型建构、解释验证;运算法则、运算策略;几何直观、空间想象;获取数据、加工数据、解释数据）[3]。

一方面，由于数学核心素养评价不同于普通的数学测试，所以先分析确定数学核心素养评价二级指标在评价模型中的权重，以构建较科学、合理的数学核心素养评价体系。另一方面，由于数学核心素养评价更多地体现为一种过程性评价，因此，有必要关注高中生在每个评价指标上的发展水平，以及高中生在不同发展水平（知识技能水平、问题解决水平、综合发展水平）上的素养表现。

3.评价维度的建立

首先，建立高中生数学核心素养评价框架，主要包括5个维度：数学内容、评价指标、水平、情境、问题类型维度。其次，根据《普通高中数学课程标准（2010年版）》确定数学核心素养评价测试问卷所涵盖的内容主题，主要包括数与代数、图形与几何、统计与概率三个方面。

二、问卷编制

数学核心素养评价测试问卷的大部分试题选自国内外已有研究，包括PISA公布的测试样题、台湾林福来教授研究团队公布的数学素养评量样本试题、数学素养评价博硕论文中使用的试题等[4-7]。这部分测试题由一批优秀的数学教育研究工作者集体研发，不仅经过实证研究的检验，而且适用于大范围素养评价的测试。

《数学核心素养预测问卷（高一～高三卷）》的选题依据即高中数学主要教学内容，每套问卷6道大题，依次考察学生的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析核心素养。具体而言，每套问卷共包括6个内容主题，有与6个任务情境相关的18道题，问卷总分值为36分，共有选择题、解答题、填空题、开放型建构题、判断题、证明题6种题型。

三、预调查问卷的分析与修订

1.预研究样本

预研究主要是对问卷的测试内容、题目难度、试题表达方式、解答情况等进行预调查，旨在让问卷更适合高中生数学核心素养评价。以随机取样的方式，在J省选取三个地区、三所学校的2041名高中生作为预研究对象，学校主要集中在主城区，且均为市一级公办学校。在参加预研究的学生中，男女比例基本相当，年级包括高一～高三，不同年级学生比例也基本相当。预研究时间由各个学校自主安排，学生在规定的时间、地点集中完成测试。共发放问卷2041份，回收问卷2041份。

2.预研究信度与效度检验

（1）信度检验

信度是测验可靠性和稳定性的指标，采用内在一致性信度测量方法，对《高中生数学核心素养预测问卷》进行信度检验，内在一致性系数反映的是量表内部的一致性，即项目同质性。检验结果表明，《高中生数学核心素养预测问卷（高一～高三卷）》三份问卷信度分别为：0.714、0.711、0.718，部分问卷指标内部一致性系数在0.8以上，有些指标项目需要修订。总体而言，预测卷能够基本达到预期的评价目的。

（2）效度检验

①内容效度

内容效度（content validity）研究的目的是要评估测试题是否充分代表了所要评价的内容范围，它所关注的是数学核心素养评价的内容方面。主要通过以下三种方式来验证数学核心素养预测问卷具有一定的内容效度：第一，预测问卷项目内容的代表性。“数学核心素养”的概念是在阅读、梳理国内外数学核心素养的相关研究文献基础上提出来的，评价指标的确定综合考虑了数学素养的核心内涵，并结合了指标调查。所以，问卷各个指标的内容，能够代表数学核心素养的研究主题。第二，预测被试对象的合理性。

问卷指标、内容初步拟定后，以讨论班的形式，请数学教育专业的部分教师和研究生评价这些测试题，同时，一线中学数学教师及相关任课教师对测试题的适宜性及可读性进行了评价，对预测结果进行统计分析和进一步访谈，再次对测试题目进行修改。问卷的修编研究所采用的被试全部是公办学校中未参加过数学竞赛辅导的高中生，具有一定的代表性。第三，预测问卷编制方法的科学性。

《高中生数学核心素养预测问卷（高一～高三）》共18个题项，每个一级评价指标3个题项，分别指向二级评价指标。问卷测试题均以国内外较为成熟的评价测试项目为依据，进行改编，不仅能保证问卷的效度，而且具有一定的科学性。

②结构效度

结构效度就是测验能说明心理学上的理论结构或特质的程度，研究采用维度分析法考察预测卷的结构效度。以高一问卷为例，考察各指标之间的相关，6个评价指标之间，绝大多数指标两两之间的相关达到了0.01的显著性水平，相关系数在0.148～0.381之间，均为正相关。6个评价指标与总问卷之间的相关在0.399～0.648之间，为中等程度正相关，表明各评价指标与问卷总体评价一致。

高一～高三问卷的统计结果表明，数学核心素养预测卷各指标之间呈中等程度正相关，各指标与总问卷之间呈中等程度正相关，数学核心素养评价各指标与问卷的整体概念一致并且具有独立的结构内涵;但需在正式问卷中对测试题修改完善，以进一步提高问卷的效度。

在预研究基础上，我们对测试卷每道题的结果都进行了分析，对问卷题量、试题难度、区分度等都进行了修改完善。

四、评价问卷的正式建立

在前期预研究的基础上，形成正式问卷《数学核心素养测试问卷（高一卷～高三卷）》。正式卷包括与6个教学任务情境相关的18道题目，问卷内容覆盖了数与代数、图形与几何、统计与概率三个内容领域，每道测试题都对应着不同的内容主题和数学核心素养评价维度。

对数学核心素养测试问卷的试题分布进行分析，三套问卷（高一卷～高三卷）格式、题例基本一致，均以评价指标顺序呈现。对数学核心素养测试问卷的水平分布进行分析，了解数学内容、素养水平和题目数量、题型之间的关系。对数学核心素养测试问卷的百分比分布进行分析，了解数学内容、素养水平和数学情境分布情况。与此同时，我们也进行了试题的示例分析和测试题评分标准的统一。

1.试题示例

（1）數学抽象试题示例

试题1：数位色彩  数学核心素养测试问卷（高三卷）

很多软件中，都会遇到设定颜色值的问题，十六进制颜色码就是在软件中设定颜色值的代码。在电脑中可用色码来表示颜色，例如（255，255，255）是指白色、（255，0，0）是指红色。判断方法为：3个数字依序代表三个原色光——红光、绿光、蓝光的亮度，（200，0，150）表示红光200、绿光0、蓝光150，合成的颜色是偏红的紫色。每种原色光的亮度以0-255之间的整数表示，数字越大代表亮度越高。

问题（1）：（127，127，127）是指什么颜色？

A.浅蓝色       B.中灰色

C.浅灰色       D.中蓝色

问题（2）：标准黄色可由亮度最高的红光和绿光合成，请写出一个“标准黄色”和一个“较偏红之黄色”的色码。

问题（3）：每种原色光都分别有256种层次，以0-255之间的整数表示。请问：一般电脑屏幕可显示出多少不同的颜色？

试题评析：该题考查的是高三学生数学抽象核心素养，问题（1）着重于数学表征素养，是一道水平1的测试试题，需要学生从色码数字中，抽象出颜色的一般规律。问题（2）较之问题（1），是一道反向表征题，素养水平2级，需要学生用数字表征出颜色色码的结构。问题（3）着重于抽象思考素养，是一道水平3的测试题，需要学生从数量之间的关系之中，抽象出颜色与色码之间的关系。

（2）直观想象试题示例

试题5：小小工程师  数学核心素养测试问卷（高二卷）

鲁夫是个电脑程序设计师，已知现在有个科学绘图程序，只要输入数学方程式即可自动绘成直角坐标图形。

问题（1）：若是鲁夫打了下列四个方程式，则电脑屏幕中的直角坐标平面出现的图形，会像什么字？

x=0（-3≤y≤3）

y=0（-2≤x≤2）

y=3（-3≤x≤3）

y=-3（-3≤x≤3）

问题（2）：若是鲁夫想绘出「二」符号，请问他必须写出哪些方程式，才可以完成这个任务？

问题（3）：若是鲁夫想绘出「？蛀」符号，请问他必须写出哪些方程式，才可以完成这个任务？

试题评析：该题考查的是高二学生直观想象核心素养，问题（1）评价学生几何直观素养，是一道水平2的测试题，需要学生利用几何图形，数形结合，解决数学问题。问题（2）评价学生空间想象素养，素养水平1级，需要学生利用空间想象，写出该符号的数学方程式。问题（3）也是评价空间想象素养，是一道水平3的测试题，需要学生数形结合，感知图形的形态与变化，写出该符号的数学方程式。

2.测试题评分标准

数学核心素养测试问卷的题型有：选择题、填空题、判断题、解答题、开放型建构题5类。前四类有明确的答案，按照评分标准评分即可;后一类属于开放题，需要独立研制评价标准。

数学核心素养测试问卷评分标准的研制过程如下：首先，由研究者拟定评分标准;其次，组织高中数学专家教师讨论，然后进行修改;再次，进行试评分，根据评分结果，完善评分标准;最后，在对预测问卷进行正式评分时，针对遇到的问题，进行讨论修改。

数学核心素养问卷的评价结果主要包括三类：一是该题的解答是否达到了预期的水平等级;二是对题目的解答情况给予评分;三是对题目的完成度，进行代码评定。

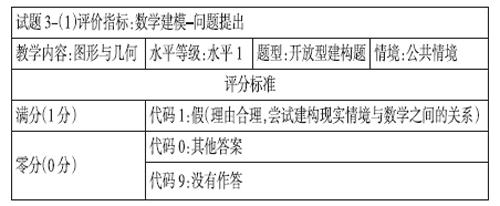
开放建构题评分标准示例

试题3：新闻真假  数学核心素养测试问卷（高二卷）

信息时代，网络上各类新闻层出不穷，真假难辨。某网站最新报道：A市某银行发生一起严重的抢劫案，劫匪独自一人在无任何车辆等交通工具的情况下，劫走现金1000万元，所有现金均为捆扎整齐的百元人民币（如图）。

问题（1）：请你判断该新闻的真假？

试题与评分编码：

问题（2）：请从数学角度（尽可能使用数学式子、数学符号和数学图形等）论证你的判断。

试题与评分编码：

问题（3）：基于以上的解答和论证，你能提出哪些新的问题？

试题与评分编码：

开放型建构题完全是开放性、建构性的，因此，在评分时，主要根据学生解答的情况，通过主观判断进行评分，评价的自由度更大一些，对学生的回答情况更多的是质性判断，量化评分。

五、经验总结

1.《数学核心素养预测问卷》的编制与试测

在数学核心素养概念的界定，以及数学核心素养评价6个一级指标、14个二级指标确定的基础上，初步确定高中生数学核心素养评价框架的5个维度：数学内容、评价指标、水平、情境、问题类型维度，共22个观测点。评价内容主题的选择，主要来源于高中数学课程内容的三个方面：数与代数、图形与几何、统计与概率。

确定了数学核心素养预测问卷的评价框架后，以国内外较大规模数学素养测试样题为依据，进行了部分测试题的改编，形成《数学核心素养预测问卷（高一卷～高三卷）》，每套问卷包含6个内容主题，有与6个任务情境相关的18道题，问卷总分均为36分，共5种题型：选择题、填空题、判断题、解答题、开放型建构题。

2.数学核心素养评价问卷的建立

通过数学核心素养评价的预研究，对数学核心素养评价问卷测试题进行修改，正式建立高中生数学核心素养测试问卷。对问卷的题号、维度、内容领域、内容主题、标题、题型、答案、分值等基本要素进行梳理。

《数学核心素养测试问卷（高一卷～高三卷）》的6个一级评价指标测试题相当;试题分布主要集中在数与代数、图形与几何领域，统计与概率方面的题较少;题型以开放型建构题、解答题为主;知识技能、问题解决、综合发展三种水平的测试题数量相当;测试题情境以教育和职业情境、公共情境、科学情境为主，个人情境次之。

结合数学核心素养评价6个一级指标，给出试题示例，并进行评析，分析试题评价的重点、水平层次以及核心素养指向等因素。通过标准拟定、教师研讨、标准完善、讨论修改四个环节，制定数学核心素养评价测试题评分标准，以测试问卷的5类题型（选择题、填空题、判断题、解答题、开放型建构题）为例，进行7个变量的评定：评价指标、教学内容、水平等级、题型、情境、评分、代码，以期对高中生数学核心素养进行全面评价。

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018：16.

[2] 施良方.课程理论：课程的基础、原理与问题[M].北京：教育科学出版社，1996：156.

[3] 陈蓓.高中生数学核心素养评价指标研究[J].教育研究与评论（中学教育教学），2019（09）：17-23.

[4] OECD.PISA2015 Draft Collaborative Problem Solving Framework[EB/OL].http：//www.oecd.org/pisa/pisa products/pisa2015 frameword

s.htm，2016-06-26.

[5] 林福來.台湾数学素养评量样本试题[EB/OL].http：//www.wendangku.net/doc/09684806ae1ffc4ffe4733687e21af45b307feef.html

[6]  苏洪雨.学生几何素养的内涵与评价研究[D].上海：华东师范大学，2009：225.

[7] 桂德怀.中学生代数素养内涵与评价研究[D].上海：华东师范大学，2011：316.

[作者：陈蓓（1981-），女，江苏常州人，江苏第二师范学院，教学质量监测与评估处，研究员，博士。]

【责任编辑  郭振玲】