Remote weak-signal measurement via bound states in optomechanical systems
Xun Li,Biao Xiong,Shilei Chao,Chengsong Zhao,Hua-Tang Tan and Ling Zhou,*
1 National Key Laboratory of Shock Wave and Detonation Physics,Institute of Fluid Physics,China Academy of Engineering Physics,Mianyang 621900,China
2 School of Physics,Dalian University of technology,Dalian 116026,China
3 Department of Physics,Huazhong Normal University,Wuhan 430079,China
Abstract A scheme for remote weak-signal sensors is proposed,in which a coupled-resonator optical waveguide (CROW),as a transmitter,couples to a hybrid optomechanical cavity and an observing cavity at its two ends.Non-Markovian theory is employed to study the weak-force sensor by treating the CROW as a non-Markovian reservoir of cavity fields.The dissipationless bound states in the non-Markovian regime are conducive to remotely transmitting a signal in the CROW.Our results show that a sensor with ultrahigh sensitivity can be achieved with the assistance of bound states under certain parameter regimes.
Keywords: non-Markovian environment,remote force detection,cavity optomechanics
1.Introduction
By using a coupling between a mechanical oscillator and a cavity field,optomechanical systems can be potentially used as high-precision instuments for detecting tiny masses and displacements along with weak forces [1,2].With the advances in micro- and nanotechnologies,micro-cavity optomechanical systems with high mechanical frequencies,high quality factors and strong optomechanical coupling have been realized in several kinds of systems such as whisperinggallery-mode resonators [3-7],levitating nanospheres [8,9]and optomechanical crystals [10-12].Such progress has pushed optomechanical detection systems into more applications.Approaches to force detection [13,14] based on nano-mechanical systems are well-established and have been used for measuring displacement [15].Increasingly,it is believed that next-generation mechanical biosensors may be realized in nano-mechanical systems,because they are particularly matched in size to molecular interactions,and provide a basis for biological probes with single-molecule sensitivity[16,17].For biosensing and medical diagnosis,or other detection scenarios,a local detection scheme might not meet the needs of practical demands.To perform remote detection,it is necessary to construct a waveguide-optomechanical coupling system.To the best of our knowledge,this type of remote force detection has not yet been investigated.
The sensitivity of optomechanical detectors is limited by noise.Various proposals have been put forward for reducing noise,including frequency-dependent squeezing of the input optical field [18,19],dual mechanical-oscillator configurations[20,21],and atom-assisted detection [22-24].In particular,it has been shown that quantum back-action (QBA)noise can be cancelled when the probe field is simultaneously coupled to positive and negative-effective-mass (NEM) oscillators [22,25-27].The QBA-free proposal has been realized in a hybrid cavity optomechanical system,in which a spin ensemble plays the role of the negative-mass oscillator [28].In this paper,we introduce an NEM oscillator to suppress back-action noise.

Figure 1.A sketch of a hybrid optomechanical system where a waveguide is coupled to an optomechanical cavity,S,and an observing cavity,O.The atomic ensemble in a static magnetic field with a specific direction can be regarded as an NEM spin oscillator (see[28]for details).
For remote detection,a waveguide is usually employed to transmit signals.Coupling to a sensing cavity using tapered fibers has been investigated in [15,29].For the purpose of integrating the system onto a chip and improving the detecting precision,a waveguide integrated into the sensing cavity has been realized in the micro-cavity regime[30,31].Theoretically,a waveguide can be treated as a structured reservoir [32-36],and the theory of non-Markovian quantum open systems is an effective method for studying the dynamics of objects coupled to the reservoir.In the cavity-quantum-electrodynamics regime,a structured reservoir can be a photonic crystal or a waveguide[34,37-41].It has been shown that bound states without dissipation can be formed when a system is coupled to bandgaps or a finite band spectrum [33,42,43]; this condition is easily satisfied by photonic crystals or waveguides [33,44,45].The dissipationless bound state benefits the transmission of signals.
In this paper,we put forward a proposal for remote force detection where a coupled-resonator optical waveguide (CROW) and a QBA avoidance technique are employed.On the one hand,due to the introduction of an NEM oscillator,back-action noise can be eliminated.On the other hand,as the transmission line between cavities,the CROW is treated as an environment shared by the cavities.Employing non-Markovian theory,we found under conditions of bound state survival,the cavity field was not ruined by an infinite degree of freedom.We further show that the output fields can be transmitted in the presence of a bound state.A high-precision sensor can be achieved for minimal weak forces.
As opposed to previous research[13,14,46]where local signal detection was investigated,we consider remote weakforce detection,which may be more suitable in some cases.In the waveguide-connected micro-cavity system described in[30,31],an output spectrum was observed when monitoring nanoparticles and tiny ambient changes,but the mechanism of the sensor was not that of an optomechanical sensor.Considering the remote transmission of signals,we investigate the conditions of existence of bound states,which are very important in practice for optimizing transmission efficiency.Furthermore,the present scheme should be experimentally feasible.It is the first proposal of optomechanical remote detection with the assistance of non-Markovian bound states,as far as we know.
This paper is arranged as follows: in section 2,we present the model and Hamiltonian of our proposal;we study the effective non-Markovian reservoir and the bound states in section 3; the sensitivity and the mechanism for suppressing noise are discussed in section 4.Finally,in section 5,we present a summary of this work.
2.Model and Hamiltonian
To detect remote weak signals,we employ a hybrid cavityoptomechanical system,as shown in figure 1.In cavity S,the movable mirror works as a sensor,and the fixed mirror of cavity S is connected to a CROW so that the signal can be transmitted to the observing cavity,O,and be read out by a homodyne detector.In addition,an atomic ensemble whose spin direction J can be manipulated by a magnetic field B is placed in cavity S.Employing the same procedure as those described in [22,28],the spin of the atomic ensemble can effectively be equivalent to an oscillator with an effective negative mass; therefore,the noise caused by quantum back action can be avoided.The Hamiltonian of the system can be written as

with
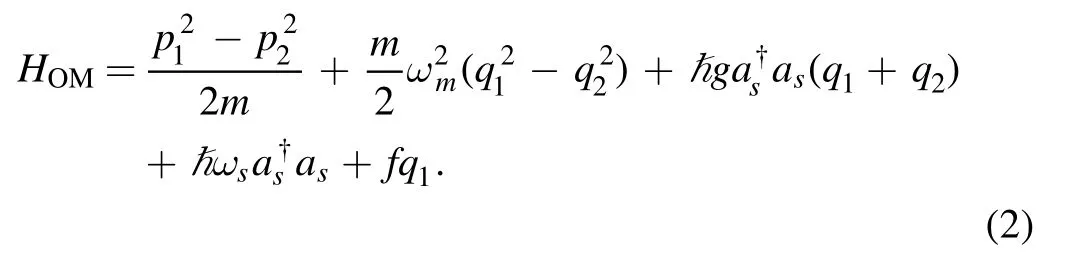
The first and the second terms express the energy of the mechanical oscillator and the NEM oscillator (a detailed description of the atomic ensemble’s equivalence to a NEM oscillator can be referred to in [28]),where q1(p1) is the position (momentum) operator of the mechanical oscillator,and q2(p2)is the position (momentum)operator of the NEM oscillator.To cancel back-action noise,we use two oscillators with the same masses (m) and frequencies (ωm) as those described in [28].The third term describes the coupling between the two oscillators and the cavity S with a coupling strength g,where the NEM oscillator couples to the field with the same form as an optomechanical interaction [47],but the positive and negative oscillators do not couple to each other,therefore,the instabilities that were investigated in [47] will not occur in our proposal.The annihilation(creation)operator of the sensing cavity S is denoted byThe fourth term is the energy of the cavity S,and the last term describes the interaction between the weak force,f,and the mechanical oscillator.
When defining the collective position Q=(q1+ q2),the collective momentumthe relative positionΦ=and the relative momentum Π=p1- p2,the Hamiltonian can be transformed into

We have the commutations [Q,Π]=0 and [P,Φ]=0.Therefore,the collective position Q (momentum P) and relative momentum Π (position Φ) are a pair of observable operators which can be simultaneously measured with arbitrary precision.
As shown in figure 1,the CROW consists of an N-cavity chain and is coupled to the optomechanical sensing cavity S and observing cavity O at its two ends.The Hamiltonian of the CROW can be written as
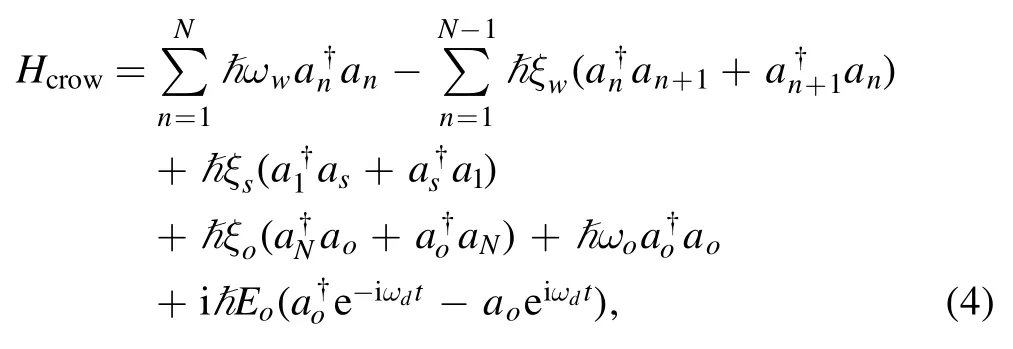
where the first term is the energy of the CROW and the second term stands for the hopping between the nearest neighbor cavity with a rate ξw.The third and the fourth terms describe the couplings of cavity S and cavity O to the 1 st and Nth cavities of the CROW,respectively,whereis the annihilation (creation) operator of cavity O.The fifth term is the energy of cavity O and the last term represents the classical driver of cavity O with frequency ωdand strength Eo.Performing the Fourier transformation [38]
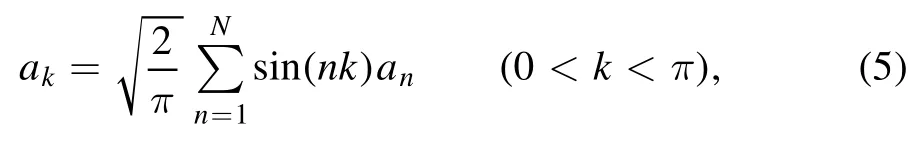
we can then rewrite the Hamiltonian Hcrowas
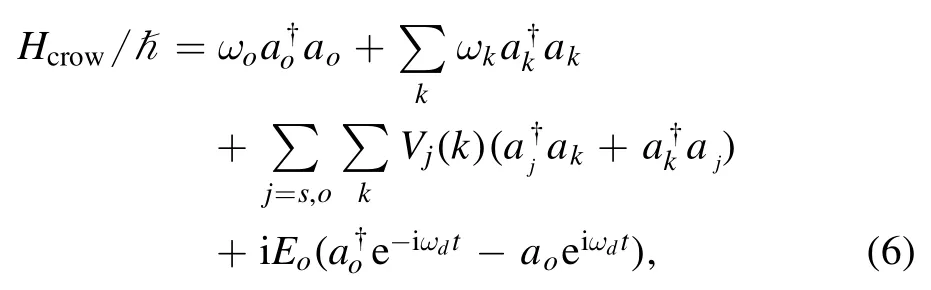
After switching into a rotating frame with respect toand nondimensionalizing the operators with the transforms:P→and Π →the Hamiltonian can be changed into a time-independent form as follows:
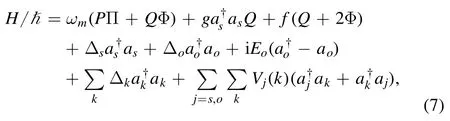
where Δj=ωj- ωd(j=s,o,k).We will use equation (7)to calculate the output of the weak signal (the weak force f).
3.The effective non-Markovian reservoir and the bound states
As we have pointed out that the coupled cavity chain is equivalent to a structured reservoir,we now solve the dynamics using non-Markovian theory.
Using the Hamiltonian equation (7),we can obtain the Heisenberg equations as
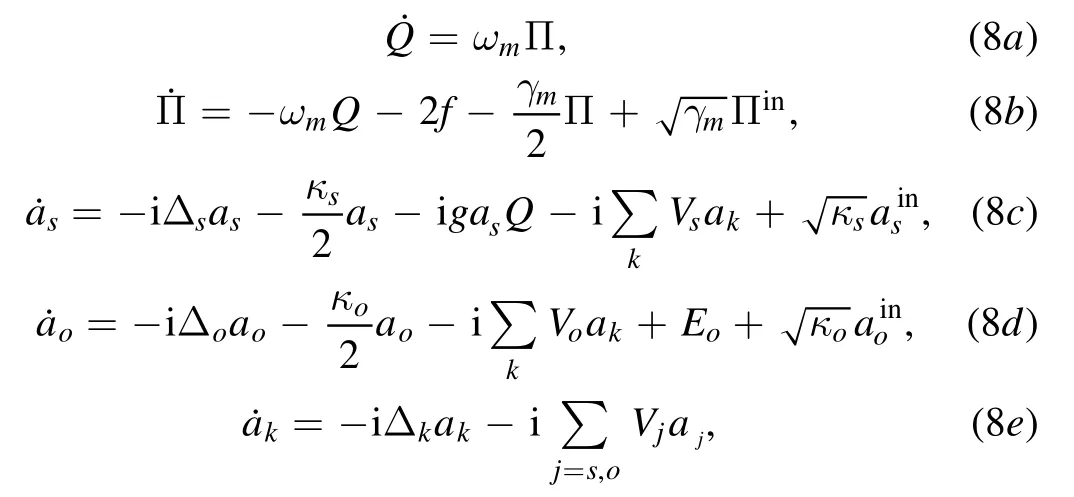
where κjand(j=s,o) are the damping rate and noise operator of the cavities S and O respectively.The negative and positive oscillators are set to the same damping,γm,andis the thermal noise of the oscillator,in whichis the noise operator of a normal (NEM)oscillator,and the correlation function has the relation=0,then 〈Πin(t) Πin(t′)〉 =From equations(8a)and(8b),it is obvious that the collective position,Q,and the relative momentum Π form a QBA-free system.Because [Q,Π]=0,the collective position,Q,and the relative momentum Π can be simultaneously measured with arbitrary precision.The variance of Q (Π)does not affect the variance of Π (Q) although the Π is related to Q (see equation (8b)).Since the cavity S (O) works as a sensor (detector),dissipation should be included,because it is an open system in order to sense the output signal,while the cavity chain functions as a transmitter.
By integrating equation (8e),the formal solution of ak(t)can be obtained:

Inserting equation(9)into equations(8c)and (8d),we obtain:
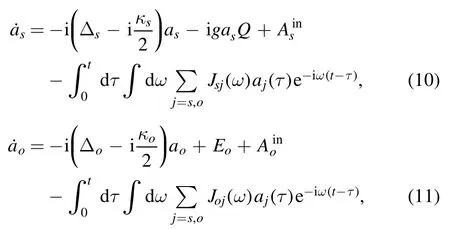
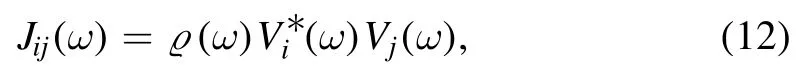
where

and
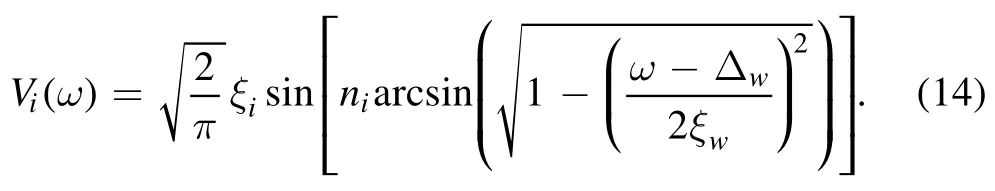
Considering the sensing cavity to be pumped with a classical field,we can expand the cavity field as aj→ αj+ aj(j=s,o),which means that the cavity field can be decomposed to the classical mean value αjplus its quantum part,so that the dynamic equation can be linearized.In the strong non-Markovian regime,αjdoes not mean the steady-state values of the cavity field aj.According to equations (10)and (11),we have
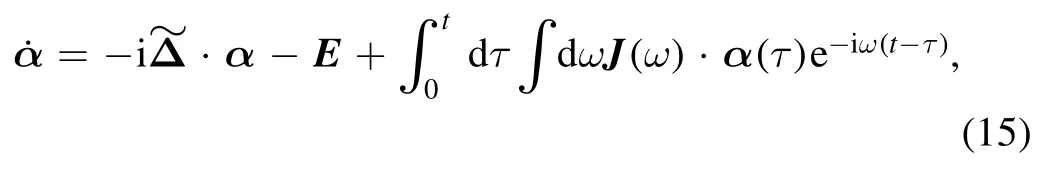
where

α(t) =[αs(t),αo(t)]T,withandE=[0 ,Eo]T.We perform the Laplace transformationto solve the dynamic evolution αj.Following the inverse Laplace transform,we obtain the solution of αsin the long-time limit


Figure 2.The frequency ωr as a function of Δs (a) and Δo (b); the blue lines represent bound states,while the red lines represent the poles leading to exponential decay.The parameters that were unspecified before are: Δw=8ωm,Δs=4ωm,Δo=2ωm,ξw=3ωm,ξs=4ωm,ξo=2ωm,Eo=2 × 105ωm,κs=0.01ωm,κo=0.05ωm g=0.002ωm,and N=30.
The first summation can survive in the long-time limit whereis a pure real number,which corresponds to the so-called bound states [42].Physically,bound states are collective states of the whole system and can be understood to be eigenstates with real eigenvalues,while in the second summation,ωrnmight have an imaginary part corresponding to exponential decay.The last term represents non-exponential decay.The exponential and nonexponential decays imply an infinite degree of freedom of the CROW,which looks like the ‘intrinsic loss’ of the CROW.A detailed description can be seen in appendix.
Since the cavity chain is equivalent to a ‘reservoir’,the‘reservoir’might induce dissipation for cavities S and O under Markovian theory.In order to transmit the weak signal,we expect that the cavity chain can transmit the signal with minimal or no dissipation.Fortunately,with a non-Markovian treatment,bound states can be formed and survive for a long time,therefore these states are ideal candidates for transmitting the signal.In other word,the bound state is important and plays a special role in remote weak-signal detection.We now discuss the parameter region in which the bound state exists.
We numerically calculate the ωr(poles of Green’s function,determined by D(z)=0; see equation ((A6) in the appendix),and plot the real part,shown in figure 2.In the green area,the condition Δw- 2ξw< ωr< Δw+ 2ξw(determined by making the radicand of equation(13)positive)is satisfied,in which exponential decay dominates αs(t → ∞)because of the large imaginary part.Beyond the green area,the poles are on the real axis,and a bound state can be formed and keep oscillating.In figures 2(a) and (b),the two blue curves correspond to the two bound states,while the red curves (in the green area) represent exponential decay.We can observe that when the two bound states have very close frequencies (or almost cross),the bound states change sharply.Under these conditions,a small disturbance can cause a jump between the two bound states.In figure 2(a),we mark the special point A,where Δs=2.4ωm,ωr1≈0(relative to the frequency of the pumping field) andωr2≈ωm,which means the one of the collective bound states resonates with the pumping field and the other resonates with the mechanical oscillator.The result is reasonable and will play an important role in weak-force detection.The behavior of the two bound states as function of Δo(figure 2(b)) is similar in figure 2(a).When Δs=2.4ωm,Δo=0.8ωm,we mark the special point B where the two bound states almost cross with very small values ofωr1andωr2.Under these conditions,the two bound states both nearly resonate with the pumping field.The point A also can be found in figure 2(b),also marked with A.We will compare the weak-force detection effect between the two special points.
4.The sensitivity of weak-signal detection
We now study the sensitivity of weak-signal detection.As we have pointed out,the bound state means long-term oscillation,which benefits the transmission of the signal.Under this condition,the coupling between the mechanical oscillator and the cavity mode asis of the formG=αsg=whereGn=corresponds to the bound statesωrnandG0=After linearization,the Heisenberg-Langevin equations can be obtained as
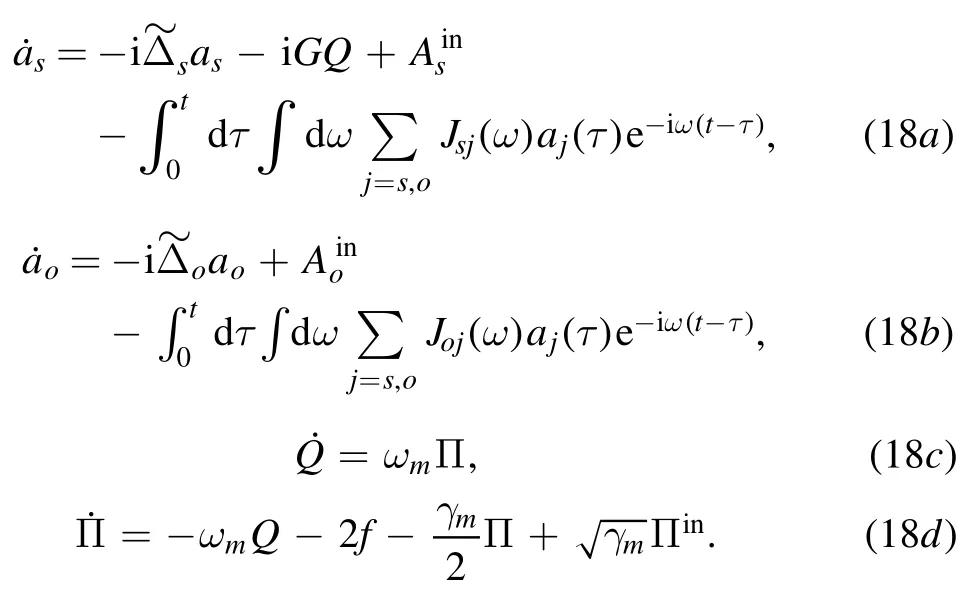
If the back-action-avoidance technique is absent,the backaction forcewill appear in equation (18d) as shown in [46],which can induce a noise channel.The above equations can be changed for the frequency domain as follows:
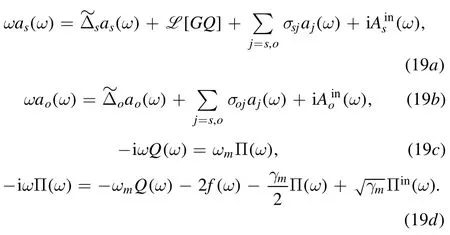
We let L[GQ] =by settingωr0= 0(ωr0is a notation,and not a bound state).According to equations (19a) and (19d),we obtain
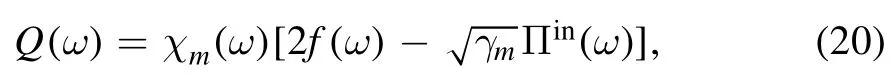

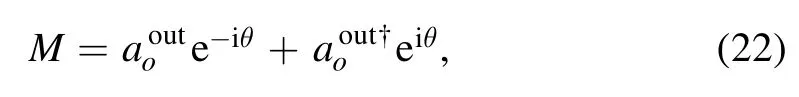
where θ is an adjustable phase.In the frequency domain,the relation between the signal and the quadrature can be obtained as follows:
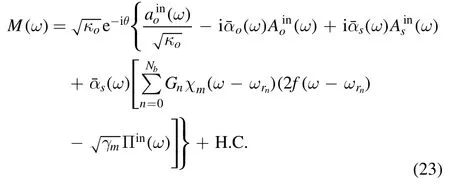
We can see that the response functionsandtaken together,determine the response to the weak signal f.The bound states shift the response frequency of ξm,and can enhance the optomechanical coupling.The signal may be amplified byas shown in equation(23).If both functions achieve their maximum values,then we can obtain the optimal response.This is why we discussed the bound state in figure 2.In addition,due to the introduction of an NEM oscillator,the back-action noise of the cavity S is eliminated,and only the thermal noise of Πinexists,in contrast to our early work [46],where the additional noise contained back-action noise in proportion to the optomechanical coupling G.We would like to amplify the signal,f,while suppressing the noise as much as possible.Therefore,the noise level is very important in weak-signal detection.We employ the definition of noise force (additional force)[22]as
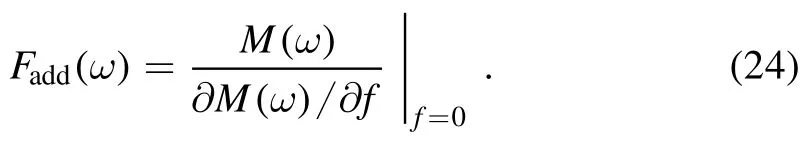
According to equation(23),the addition force can be obtained as

where
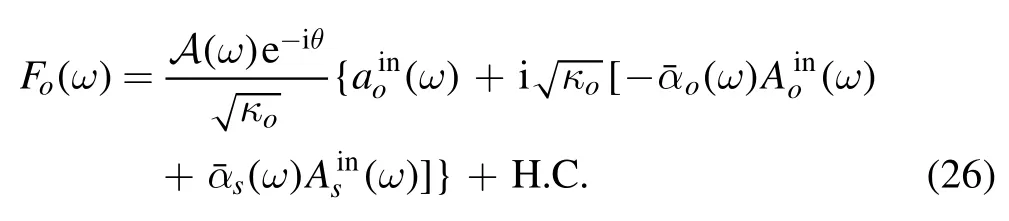
is the noise induced by the cavity fields,in which

The noise spectrum can defined as
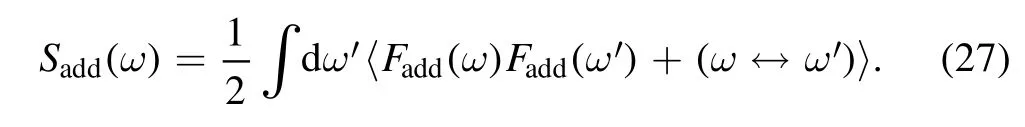
If the signal is much weaker than the noise,it cannot be separated from the background noise.Therefore,the noise level determines the accuracy of weak-signal detection.Therefore,it is reasonable to define the force sensitivity using
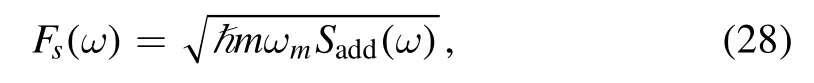
where ħmωmis introduced to recover the units because we nondimensionalized the Hamiltonian based on ωmand ħ [48].The thermal noise operator,Πin,is a statistical mixture of the thermal noise of the positive and negative oscillators.Considering that the positive and negative oscillators have the same frequency and damping rate,the correlation function in the frequency domain can be obtained as
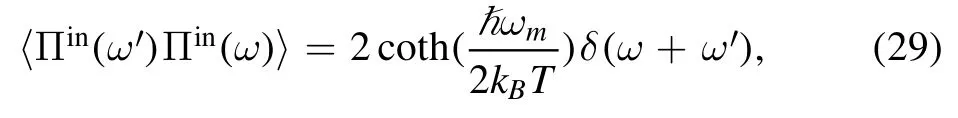
where T is the temperature and kBis the Boltzmann constant[49].The noise operator for the cavity fields consists of two parts,whose correlation functions are
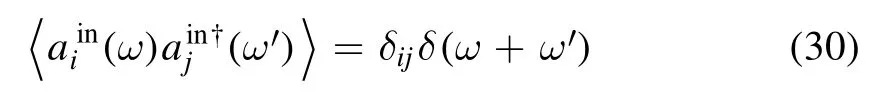
and
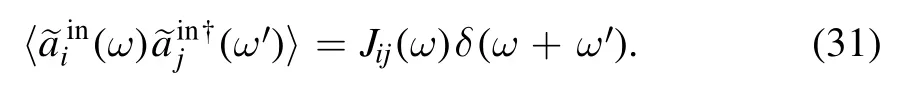
We can obtain the additional noise spectrum as
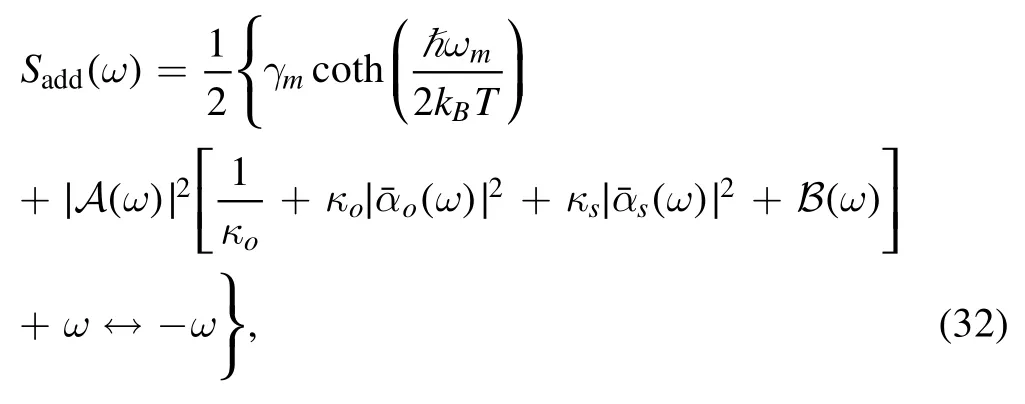
where
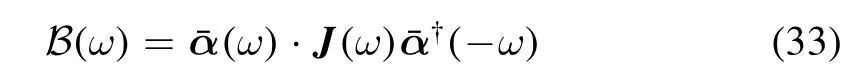
stands for the noise induced by the non-Markovian reservoir.When ω < Δw- 2ξwor ω > Δw+ 2ξw,which fall outside the defined spectrum,B(ω)will vanish,and the corresponding noise is eliminated.However,the disappearance of B(ω)does not mean the noise has been minimized,because other noise in equation (32) may be amplified when B(ω)vanishes.
We now investigate the optical noiseFso,part of the sensitivity Fs,where we temporarily ignore the thermal noise of the oscillator.In figure 3(a),we show the optical noise,Fso,as a function of ω with several values of Δs.For the green curve,a bound state corresponding to exponential decay vanishes,which was discussed for figure 2(a).When Δs=2ωm(corresponding to the blue curve in figure 3(a)),we can find theωr1≈-0.29ωm(relative to the frequency of pump field ωd) andωr2≈ωm(see figure 2(a)).Since one of frequency of the bound states is different from ωm,we can observe several dips.For Δs=2.4ωm,we haveωr1near zero andωr2≈ωm(corresponding to the point A in figure 2(a)).In this case,the red curve shows an ultrahigh sensitivity over a wide range of frequencies.Comparing the red line and the blue line,the two bound states are closer to the crossing point for Δs=2.4ωmthan for Δs=2ωm.Therefore,the sensitivity with bound states(the blue and red curves)is better than that without bound states.
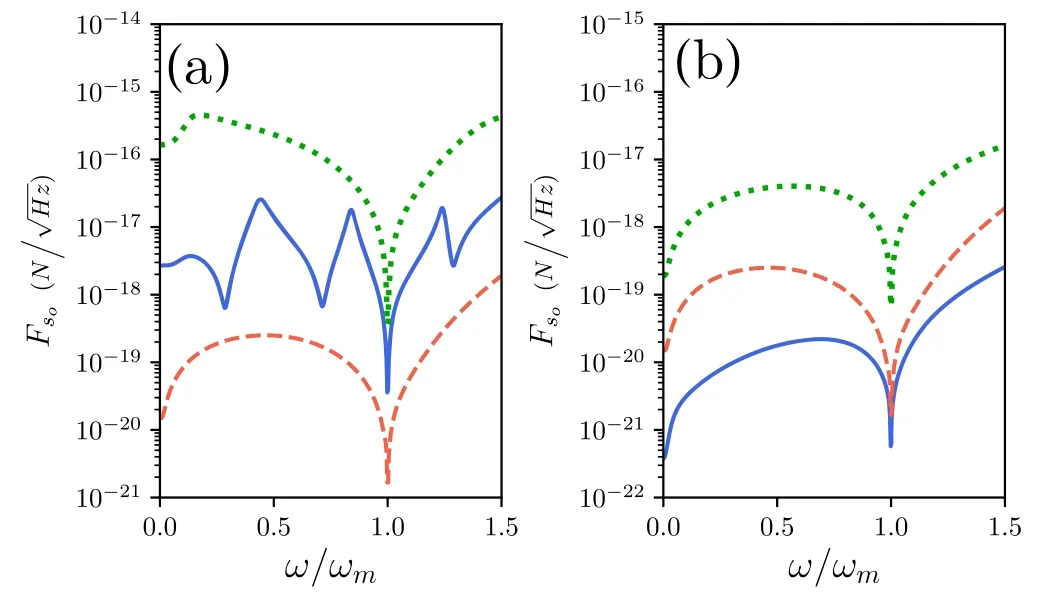
Figure 3.The sensitivity of the sensor (without thermal noise) as affected by several parameters where: (a) Δs=2ωm (blue solid line),2.4ωm (red dashed line),8ωm (green dotted line),and (b)Δo=0.8ωm (blue solid line),2 ωm (red dashed line),and 6ωm(green dotted line),where Δs=2.4ωm in (b).When bound states occur and satisfy the frequency condition,in particular,ωr1≈ωr2≈0 (the blue solid line in (b)),the sensitivity is optimized.Here,γm=10-5ωm,ωm/2π=0.5 GHz,m=1.4 × 10-18 kg and θ =π/2.Other unspecified parameters are the same as in figure 2.
In figure 3(b),we investigate the sensitivity with different values of Δo,where we choose Δs=2.4ωm.For the green dotted line,only one bound state exists.The red dashed line is the same as that in figure 3(a) with the same parameters(corresponding to point A in figure 2(b)).For the blue line,Δo=0.8ωm,the frequencies of the two bound states are almost at the crossing point,with very small values ofωr1andωr2(but not zero,corresponding to point B in figure 2(b)).The sensitivity around the crossing point is even higher than that shown for the red line.Whenωr1is very close to zero,αs(∞)is greatly amplified,at which point,the effective optomechanical coupling is enhanced becauseMeanwhile,the other bound state withωr2≈ωmis resonant with the optomechanical oscillator.Therefore,we can achieve ultrahigh sensitivity.If the two bound states both resonate with the pumping field,the value of G is jointly amplified with two very small values ofωr1andωr2,therefore,the sensitivity around the crossing point is higher than that with one small value ofωr1.
Taking thermal noise into account,we plot the total sensitivity,Fs,in figure 4.When detecting a signal at room temperature,without a bound state (blue dashed line),Fso(ω)is much larger than the thermal noiseFth≈except for the frequency around ωm,and the optimizedFso(ω)in our scheme (the blue solid line)is limited by Fth.In weak-force sensing with general optomechanical systems (without back-action avoidance),photon shot noise and quantum back action lead to the so-called standard quantum limit (SQL),(see[22]).As shown in figure 4,the level of SQL is higher than thermal noise at room temperature.With back-action avoidance,we can see that the induced optical noise is almost zero because at the lowest point,the sensitivity is only limited by thermal noise.That is to say,our proposal is better than generic optomechanical sensors,even at room temperature.When T=3 K,thermal noise also dominates the sensitivity.We can calculate the sensitivityFs≈ 4×,shown in fgiure 4.When T=30mK,the optical noise significantly impacts the additional noise,especially in the high-frequency regime.When cooled to 3mK,where the thermal phonon number nth≈ 2.5,the sensitivity is very close to that at a temperature of zero.
In optomechanical crystals,high quality factors for the cavity and oscillator have been realized,along with strong optomechanical coupling [1].Optomechanical systems with embedded spin have also been reported [50],which may be applied to on-chip force sensors that are free of back action.If the oscillator can be placed in a pre-cooled bath[51],thermal noise can be suppressed and our proposal can reach an ultrahigh sensitivity.Even at room temperature,our proposal is better than generic optomechanical sensors over a wide range of frequencies,as a higher sensitivity can be achieved for the same driven field,so that optically induced heating can be suppressed.Our scheme provides a candidate for remotely sensing quantum signals or weak forces.
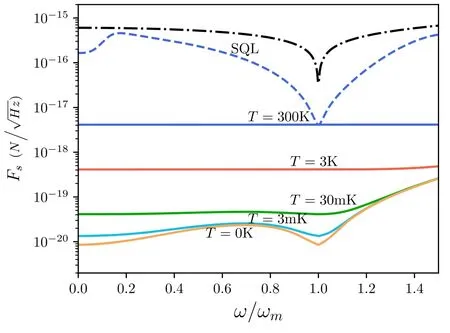
Figure 4.Sensitivity spectra for different temperatures.The parameters of for the solid lines are same as for the blue line in figure 3(b).The black dashed and dotted line represents the SQL of optomechanical detection where thermal noise with T=300 K is included.The dashed line corresponds to the green dotted line in figure 3(a) without a bound state,whose sensitivity is limited to With the optimized bound states,larger detection widths and higher sensitivities can be achieved.The other unspecified parameters are the same as those used for figure 2.
5.Conclusions
In conclusion,we have provided a proposal for a high-sensitivity remote weak-force sensor in which the hybrid optomechanical system is back-action free through coupling to an NEM oscillator.After back-action noise was canceled by the NEM oscillator,we sought an efficient signal-transmission method.A CROW was employed to transmit the output field from the sensing cavity to the observing cavity.To improve the sensitivity of remote detection,we carefully investigated the condition of bound states where the dissipation of the CROW was balanced by the pumping of cavity O.By tuning the detuning of the cavity,we were able to choose optimized bound states.With the assistance of bound states,an ultrahigh sensitivity was achieved with optical noise smaller than the zero-point fluctuation.In the frequency domain,high-sensitivity detection was not only achieved at ω≈ ωmbut also over a wide range of frequencies.Even at room temperature,the optimized sensitivity with a bound state was much lower than without a bound state.When the temperature was near 3mK,the sensitivity reachedIn our investigation,we did not include the oscillator compression technique,and we omitted the loss due to the CROW.If we were to introduce the compression technique and take account of the loss of the CROW,the noise of the CROW might be canceled out by the noise suppressed using the compression technique.
Acknowledgments
This work was supported by NSFC under Grant Nos. 11874099 and 11 674 120.
Disclosures
The authors declare no conflicts of interest.
Appendix.Bound states and the long-time solution for the classical mean value
In this section,we study the Green’s function of the cavity field,and the positions of the poles of the Green’s function.
Performing a Laplace transform on equation(15)with an initial value α(0)=0,we can obtain
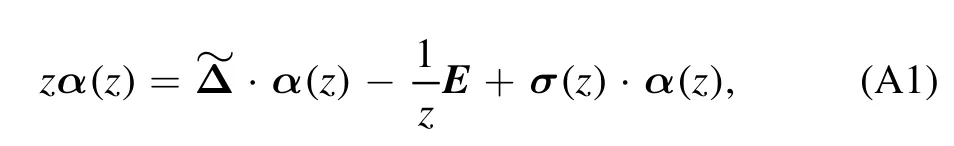
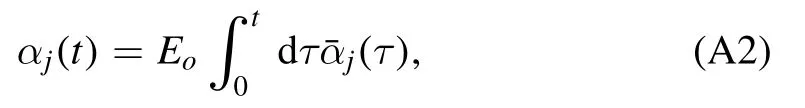
whereis the corresponding Green’s function.The Green’s functionobeys the Dyson equation
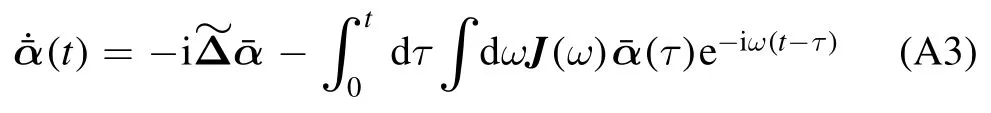
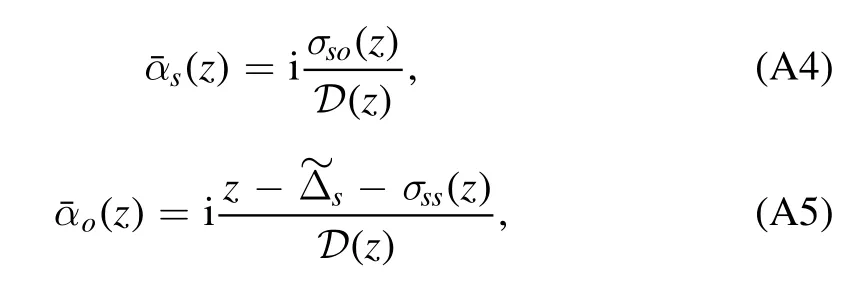
where
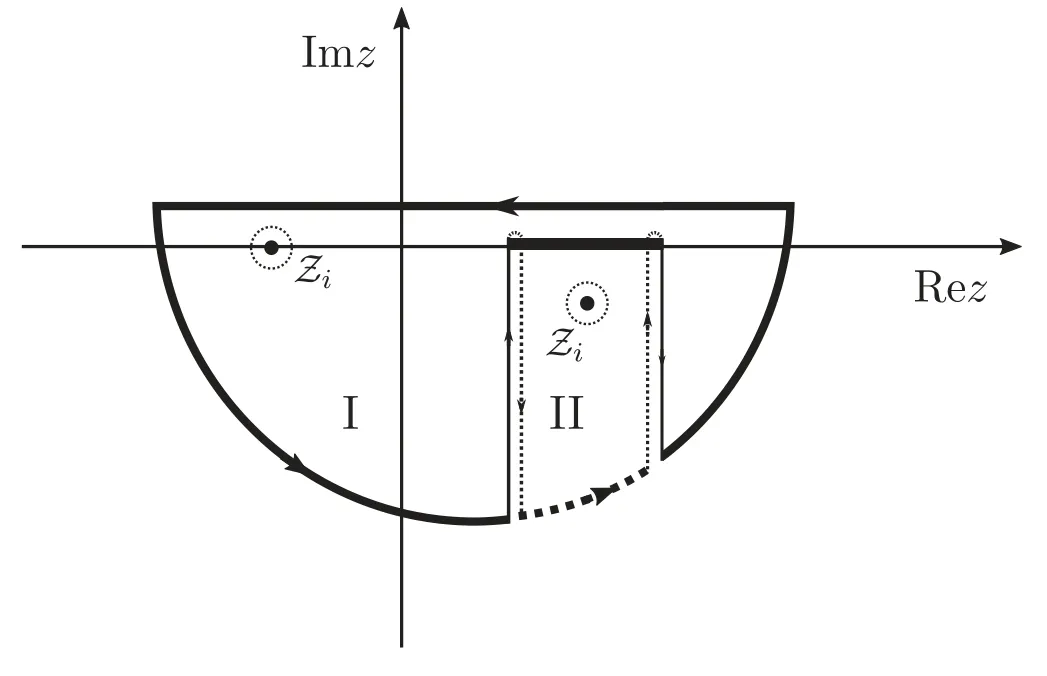
Figure A1.The Bromwich path for the inverse Laplace transformation.
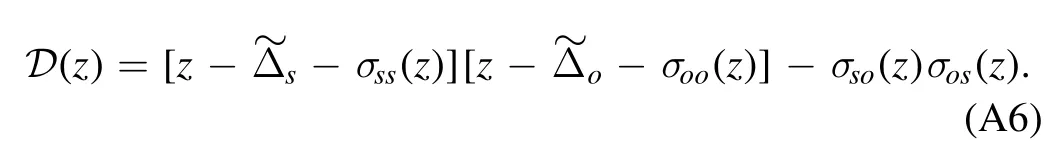
Thecan be solved through an inverse Laplace transformation
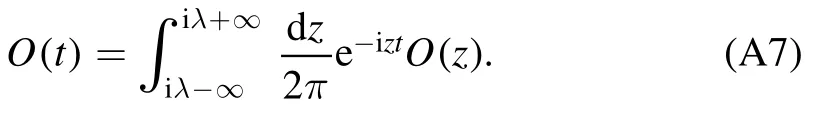
The integral on the complex plane should be calculated using the contour integral technique around the Bromwich path,which is presented in figure A1.For our system,is not analytic on the complex plane where Δw- 2ξw< z < Δw+ 2ξwis the branch cut.The contour path crosses the branch cut at Δw- 2ξwfrom the first Riemannian sheet I to the second Riemannian sheet II and back from II to I at Δw+ 2ξw,guaranteeing that the integrand is analytic.On the second Riemannian sheet,we define the analytic continuation of σij(z),as previous papers pointed out [33].If,taking the dissipation of the CROW into consideration,a tiny decay term - κwakis added into equation (8e) with the decay rate κwof every cavity of the CROW,Δkin equation (9) should be replaced by Δk- iκw.Finally,the dissipation will slightly shift by z on the imaginary axis,which will not change our conclusions.
With the inverse Laplace transform of equation(A4)and the contour integral technique,we obtain

where Znare the residues ofcorresponding to the pole atz=ωrnon the first and the second Riemannian sheet,and the last term describes the non-exponential decay.
According to equations (A8) and (A2),we can obtain αs(t).In particular,we focus on the long-time limit αs(t → ∞) which plays a key role in our proposal.The fast decay terms of αs(t) are negligible,thus we can obtain
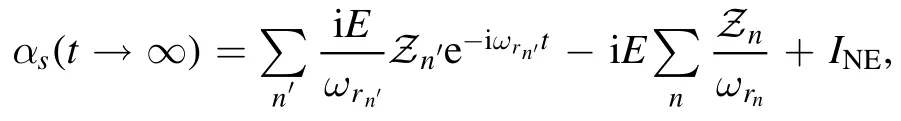
where only the poles corresponding to the bound state contribute to the first term with notationn′,the second term takes all the poles into consideration with notation n,and the last term
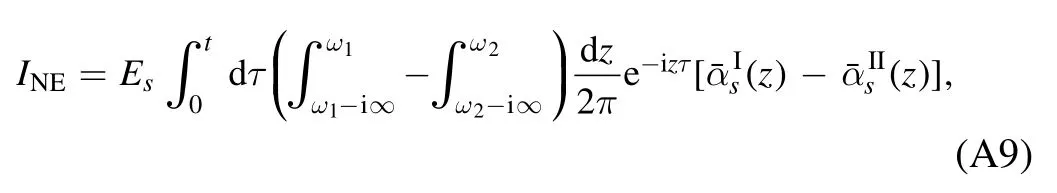
is contributed by non-exponential decay.
ORCID iDs
 Communications in Theoretical Physics2021年2期
Communications in Theoretical Physics2021年2期
- Communications in Theoretical Physics的其它文章
- Interacting tachyonic scalar field
- Mono-top signature from stop decay at the HE-LHC
- Study of K*(892)0 and φ (1020) meson production in proton-proton and Pb-Pb collisions at 2.76 TeV
- Bouncing scenario of general relativistic hydrodynamics in extended gravity
- Superconducting gap ratio from strange metal phase in the absence of quasiparticles
- Site preference of Ti and Nb in L12-ordered Co-Al-W phase and their effect on the properties of the alloy: first-principles study
