Site preference of Ti and Nb in L12-ordered Co-Al-W phase and their effect on the properties of the alloy: first-principles study

Zihan Wang,Jianxin Zhang,Pan Li,Youjian Zhang,Huixin Jin and Wenyang Zhang

Key Laboratory for Liquid-Solid Structural Evolution & Processing of Materials (Ministry of Education),School of Materials Science and Engineering,Shandong University,Jinan 250061,China

Abstract In this work,the equilibrium structure,electronic and elastic properties of L12-ordered Co-Al-W and Co-Al-W-X (X=Ti and Nb) phase were calculated,using first-principles calculations.Among six nonequivalent sites(Al1,Al2,Co3,Co4,W5,W6),Ti and Nb prefer to occupy the W6 site,since the formation enthalpy of the system is lowest when Ti and Nb occupy the W6 site.Both Ti and Nb most affect the density of states of Al atoms.Compared with the Al2 site,which is the sub-preference site of Ti and Nb,the density of states of Al atoms is higher with the addition of Ti and Nb in the W6 site,which means that the latter system is more stable.According to the bulk modulus B,shear modulus G,Young’s modulus E,hardness HV and Poisson’s ratio σ,for Co3(Al,W) alloy,the addition of Ti and Nb in the W6 site decreases its hardness but increases its ductility.This work confirms that Ti and Nb can stabilize the Co3(Al,W)alloy and have a positive effect in solving the relatively poor ductility of this alloy,which has important implications for the development of cobalt-based alloys.

Keywords: Co-Al-W phase,equilibrium structure,electronic and elastic properties,firstprinciples study

1.Introduction

Superalloys are a special type of high-temperature-resistant material that can work in complex stress and corrosive environments at temperatures above 800°C.In this class,the successful application is the nickel-based superalloys,which are widely used in turbine blades and engines [1,2].As a stable microstructure that contains cuboidal L12-ordered γ′-Ni3Al coherent precipitates appearing in a face-centered cubic(fcc)γ-Ni matrix,these alloys possess sustained high-temperature strength [3].However,for high-temperature alloys,high-temperature strength is not enough,and hot corrosion resistance is also required,since hot corrosion and oxidation are an important cause of material loss and performance degradation[4].In order to deal with the problem of hot corrosion,special coatings are used on nickel-based alloys,but such coatings are expensive and require high stability in longterm use [5,6].Therefore,an alloy with both high-temperature strength and hot corrosion resistance is required.

Cobalt-based superalloys have excellent resistance to hot corrosion.They can form dense oxide scales to protect the internal metal from corrosion [7-9].However,the mechanical strength of nickel-based alloys is higher than that of cobaltbased alloys,which limits the application of cobalt-based alloys.The mechanical properties of cobalt-based alloys can be improved by adding solid solution elements and carbides to the alloys [10,11].The Co3Al phase does not exist in the binary Co-Al phase diagram[12].However,Sato et al discovered the L12-ordered Co-Al-W phase,which is similar to the γ′phase in the nickel-based alloy in the cobalt-based superalloy,which sets the goal of studying the cobalt-based superalloy[11].The thermodynamic stability of γ′-Co3(Al,W) with the addition of Ta and Hf was studied,and it was found that an addition of up to 2.2 at.%Ta does not change the phase equilibria in the Co-Al-W ternary system,but a small addition of Hf stabilizes the γ′phase[13].Elemental partitioning and mechanical properties of Ti- and Ta-containing Co-Al-W-based superalloys was studied by atom probe tomography and nanoindentation [14].In cobalt-based superalloys,Ti,Ta,Nb,Mo and V tend to enter the γ′ phase and increase the solvus temperature of the γ′phase,whereas Cr,Mn,Fe and Re tend to enter the γ phase and lower the solvus temperature [15-19].In some cases,the strength of the cobalt-based superalloy is close to the strength of the existing nickel-based superalloy [12].

In the past decade,the first-principles method has become an important method for studying the phase stability,mechanical and thermodynamic properties of crystalline materials [20-22].Some properties of L12γ′-Co3(M,W) (M=Al,Ge,Ga) have been studied through the first-principles method,which indicates that the γ′ precipitate has a positive significance for improving the performance of cobalt-based alloys [21-24].Ti and Nb are often added to the γ′precipitate.They are found to be the most effective in improving the γ′ solvus temperature of Co-Al-W based alloys and are γ′-forming elements which enhance the volume fraction of the γ′ phase [15-17].The current Co-Al-W based alloy has a main deficiency,which is relatively poorer ductility compared to a nickel-based superalloy[25,26].Ti and Nb have an effect on its mechanical properties and probably solve this problem.In addition,the site preference behavior of Ti and Nb in γ′ precipitates and the interaction with their nearby atoms play an important role in improving the performance of γ′precipitates,so we perform a first-principles study on the phase stability,elastic and electronic properties and site preference of the L12-ordered Co3(Al,W)precipitate doped with Ti and Nb in this work.

2.Theoretical methods

2.1.Computational details

In the unit cell of A3B compound with the cubic L12structure whose space group is Pm3m,A atoms are located at face centers and B atoms are at cube corners[27].In this work,the chemical formula is assumed as Co24(Al4,W4),which has six nonequivalent positions (Al1,Al2,Co3,Co4,W5,W6) for the substitution by Ti and Nb,as shown in figure 1.The composition of Co24(Al4,W4) is similar to the value of γ′ precipitates measured in the experiment [11,13,14].

In this work,the first-principles method,which is based on the density functional theory (DFT) [28],was applied.The Cambridge Serial Total Energy Package (CASTEP) [28] program was used to perform all the calculations.The generalized gradient approximation (GGA) with Wang parameterization(PW91) and ultra-soft pseudopotential of Vanderbily-type were adopted.The plane wave cut-off energy and k-point were 400 eV and 3 × 3 × 3,respectively.The Broyden Fletcher Goldfarb Shanno(BFGS)method[29]was applied to relax the structures.The geometry optimizations were considered to be converged when the energy change per atom,maximum force,maximum stress and maximum atomic displacement were less than 1.0 × 10-5eV,0.03 eV Å-1,0.05 GPa and 0.001 Å,respectively.The specific parameters in elastic constant calculation are energy 2.0 ×10-6eV/atom,maximum force 0.006 eV Å-1,maximum atomic displacement 0.0002 Å and maximum strain amplitude 0.003.The spin polarization is considered.

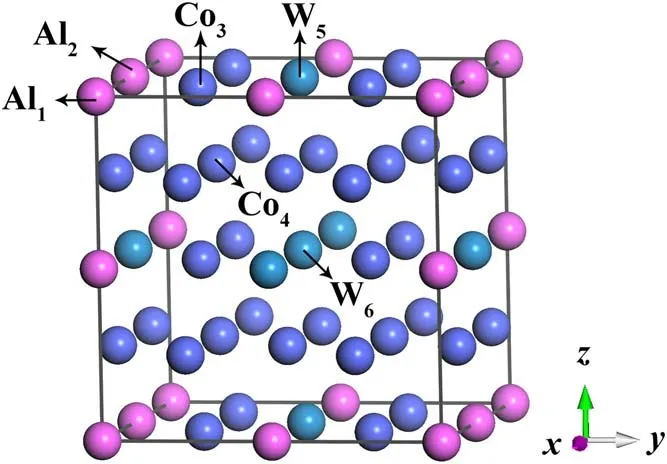
Figure 1.Crystal structure of L12-ordered Co3(Al,W) phase.

Table 1.Calculated structural properties of Co3(Al,W) phase,including lattice constants a and c,formation enthalpy H.

2.2.Elastic properties

The elastic constants can reflect the deformation resistance of a material caused by external stress and express some mechanical properties.The Young’s modulus E,shear modulus G,Poisson’s ratio σ and bulk modulus B can be acquired by the Voigt-Reuss-Hill method [30],which is considered to be a good method to evaluate the theoretical polycrystalline elastic modulus.

Figure 2.The DOS of pure Co3(Al,W)and doped Co3(Al,W):(a)the pure Co3(Al,W);(b)the DOS of Al with addition of Ti or Nb in the Al2 or W6 site; (c) Ti in the W6 site; (d) Ti in the Al2 site; (e) Nb in the W6 site; (f) Nb in the Al2 site.

The upper and lower limits of the polycrystalline constants are the values obtained by the Voigt and Reuss equations [31].Thence,the shear and bulk moduli are estimated by the arithmetic mean values of the Voigt and Reuss moduli [31].

For cubic [32]:

The hardness of materials can be correlated with the product of the squared Pugh’s modulus ratio (k=G/B) and the shear modulus [33]:

3.Results and discussion

3.1.Structural properties

In order to analyze the stability of the pure system and doped system,the formation enthalpy (H),which is equal to the energy of formation at 0 K temperature and 0 GPa pressure when the zero-vibration contribution is much smaller than the formation energy,was calculated.A negative H value indicates that the system is stable.The lower formation enthalpy demonstrates a more stable system,which can be applied to assess site replacement behavior of Ti and Nb in Co-Al-W phase.The formation enthalpy can be assessed by the following equation [34-36]:

where Etotis the total energy of the supercell,niis the number of i atom in the supercell,and Eatom(i)is the energy per atom of bulk i.Here,the hexagonal close packed(hcp)structure for Co and Ti,face-centered cubic (fcc) structure for Al,and body-centered cubic (bcc) structure for W and Nb are considered as their most stable elemental phases.

Figure 2.(Continued.)

The lattice constants (a and c) and formation enthalpy(H)of the pure system and doped system are shown in table 1.Our calculation results are similar to others’ calculation results and experimental results,which shows that our calculation results are credible [11,37].It can be seen that Co3(Al,W)with Ti and Nb replacing any atom in six sites is stable,since their formation enthalpy are all negative.However,compared with the pure system,only when Ti is in the site of Al1,Al2,Co3,W5and W6,and Nb is in the site of Al2,W5and W6,is the value of formation enthalpy lower.This shows that doping in these sites can make the original system more stable.Ti and Nb show the strongest preference for the W6site,followed by the Al2site,since the system has the lowest formation enthalpy when Ti and Nb occupy the W6site.Among the six substituted sites,the lattice constants of the system with the Co3and Co4site replaced change more than that of others,as Ti and Nb at these two sites make the symmetry of the system slightly worse.However,the lattice constants change very little,before and after doping,which signifies that the addition of Ti and Nb has little effect on the structure of the system.

3.2.Electronic structures

The density of states (DOS) and partial density of states(PDOS) of the L12Co-Al-W and Co-Al-W-X (X=Ti and Nb) phases were calculated,providing information on the physical basis for the phase stability.The DOS of the pure system and the most stable (Ti or Nb is in the W6site) and second stable(Ti or Nb is in the Al2site)doping systems are shown in figure 2.The level at zero energy is the Fermi energy level(EF),which is described by the dotted line and is defined to be the highest energy level occupied by the valence electrons at 0 K.The density of states corresponding to the Fermi surface is not zero,indicating that both pure and doped systems are conductive phases[38].The pseudogap that is the deep valley close to EFappears in both the pure system and the systems with Ti or Nb occupying the W6or Al2site,which means that these alloys show a little covalent feature[39].What is more,their EFlocates in the valley or the left of the pseudogap,demonstrating that both pure and doped systems are stable[38].According to the partial density of states,this shows that the major valence electron contributions to the bonding electrons in the whole regions are Co (3d),Al (3p),W (5d),Ti (3d) and Nb (4d).The hybridization of Al and W mainly occurs at -7.5 eV ～-5 eV and -5 eV ～-2.5 eV.Co and W mainly hybridize around -1.5 eV.Doping Ti and Nb has little effect on Co and W atoms,but has a great effect on Al atoms,for the density of states.In figure 2(b),the DOS value of Al atoms in the system with Ti occupying the W6site is greater than that in the system with Ti doped in the Al2site,indicating that the former system is more stable[40],which is consistent with the previous result that is acquired from the formation enthalpy.In addition,the pseudogap of the former is narrower than that of the latter,which reveals that the bond of the former is more metallic than the latter[38].The effects of Nb on the Co-Al-W phase are the same as Ti since their DOS are similar.

Figure 2.(Continued.)

Table 2.Calculated elastic stiffness constants Cij(GPa)and elastic compliance matrix Sij(1/GPa)of Co3(Al,W)and Co3(Al,W)with Ti or Nb doping.

3.3.Elastic properties

As the most stable structure is when Ti and Nb occupy the W6site,followed by the Al2site,this section studies the mechanical properties in these two cases.The structures of the Co-Al-W and Co-Al-W-X (X=Ti,Nb) phases are cubic.Table 2 shows the elastic stiffness constants and elastic compliance matrix of them.The corresponding mechanical stability conditions are [41]:

It is obvious that the Co-Al-W and Co-Al-W-X (X =Ti,Nb) phases satisfy the above conditions,indicating that they are all mechanically stable.As the value of C11is larger than that of C12and C44,for both the pure system and doped system,they are all very incompressible under uniaxial stress along x axis [31].

Figure 3.The elastic properties of pure Co3(Al,W) and doped Co3(Al,W) with Ti and Nb occupying the Al2 and W6 site: (a) the bulk modulus B,shear modulus G and Young’s modulus E; (b) the hardness HV; (c) the ratios between bulk modulus and shear modulus B/G;(d) Poisson’s ratio σ.

The bulk modulus B and shear modulus G reflect the ability to withstand the volume change under pressure and shear deformation under shear pressure,respectively [42].In figure 3(a),the values of B and G decline (increase),with the occupation of Ti and Nb in the W6(Al2)site,which means that the resistance ability to volume change and shape change by applied pressure is reduced(improved).Young’s modulus E can be used as a qualitative indicator to reflect the hardness of a material,and a large value of E indicates that the solid is hard[43].It shows that with adding Ti and Nb in the W6site,the values of E decline,which clarifies that the hardness of the doped system decreases.This is consistent with the content in figure 3(b),which is that the HVvalue reduces with the addition of Ti and Nb in the W6site.However,the change of E and HVvalue in the system of the Al2site occupied by Ti and Nb is the opposite.The hardness of a metal is generally expressed by its resistance to local deformation[44].It is obvious that Ti and Nb occupying the W6site weaken the ability of the alloy to resist deformation,compared to the Al2site.The ratios between bulk modulus and shear modulus B/G and Poisson’s ratio σ reflect the brittleness and ductility of a material[42].A high(low)B/G value signifies a tendency for ductility(brittleness),and 1.75 is a key value to assess ductility and brittleness [42].In figure 3(c),all the B/G values are larger than 1.75,which indicates that both the pure system and doped system are ductile.Poisson’s ratio σ(-1 ＜σ ＜0.5)can represent the shear resistance of a material[45].A high Poisson’s ratio σ means that the material has good plasticity[45].Figure 3(d)shows that Ti and Nb occupying the W6(Al2)site are able to enhance(decrease)the plasticity of the alloy,probably since the system doped in the W6site is more metallic than that in the Al2site,which is stated in the section on electronic structures.The ductility is closely related to the fracture mechanisms and embrittlement,and generally,achieving high σ is regarded as an approach to improve the toughness[46-48].It is obvious that Ti and Nb occupying the W6site result in less likelihood of fracture and embrittlement,which provides the direction of the design of the Co-based alloy.

4.Conclusions

The present work was carried out for the equilibrium structure,electronic and elastic properties of the L12-ordered Co-Al-W and Co-Al-W-X(X=Ti and Nb)phases,using first-principles calculations.It is found that in doping Ti and Nb to any of six nonequivalent sites,the formation enthalpy of these systems are negative.However,compared with the pure system,the doped system with Ti and Nb occupying the W6site is the most stable,followed by the Al2site,as the formation enthalpy are most negative.Therefore,Ti and Nb prefer to occupy the W6site in the Co-Al-W phase.Ti and Nb most affect the DOS of Al atoms and the DOS shows that the system with the W6site doped is most stable.The addition of Ti and Nb in the W6(Al2)site declines(increases)the hardness and the resistance to volume change and shape change of the alloy and improves(reduces) the ductility of the alloy.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Numbers 51971118,51771102,51471098).