Entanglement of two Jaynes-Cummings atoms in single-excitation space

Ya Yang,Yan Liu,Jing Lu and Lan Zhou

1 Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education,Department of Physics and Synergetic Innovation Center of Quantum Effects and Applications,Key Laboratory for Matter Microstructure and Function of Hunan Province,Hunan Normal University,Changsha 410081,China

2 College of Physics and Electronic Engineering,Hengyang Normal University,Hengyang 421002,China

Abstract We study the entanglement dynamics of two atoms coupled to their own Jaynes-Cummings cavities in single-excitation space.Here,we use concurrence to measure atomic entanglement,and consider the Bell-like states to be initial states.Our analysis suggests that collapse and revival take place in entanglement dynamics.The physical mechanism behind entanglement dynamics is periodic information and energy exchange between atoms and light fields.For the initial Bell-like states,evolutionary periodicity of the atomic entanglement can only be found if the ratio of the two atomcavity coupling strengths is a rational number.Also,whether there is a time translation between two kinds of initial Bell-like state depends on odd versus even numbers of the coupling-strength ratio.

Keywords: cavity optomechanics,Jaynes-Cummings cavities,single excitation,entanglement dynamics

1.Introduction

It is well known that entanglement is a typical quantum property of compound systems.It plays an essential role in quantum information science,e.g.,in quantum computation,quantum cryptography,quantum communication,and quantum measurement [1].However,quantum entanglement is very fragile,since the entangled systems inevitably interact with their surrounding environments [2].Decoherence is recognized as a major obstacle to realizing quantum information processing[3].

In recent years,the dynamic behavior of entanglement under environmental influences has been the subject of extensive research[4-9].Yu and Eberly have shown that two initially entangled but subsequently non-interacting qubits can become completely disentangled in a finite time[10-12].This phenomenon is usually called ‘entanglement sudden death’ (ESD),and has been detected in the laboratory [13].Subsequently,the creation or rebirth of entanglement has been found in a two-qubit system[14,15].Later,the dynamic properties of entanglement were also investigated for threequbit states [16,17].

The Jaynes-Cummings (JC) model describes coherent interaction between a two-level atom and a single radiation mode[18].In the single-excitation subspace,the JC model is equivalent to a two-qubit system.As one of a few exactly solvable models,the JC model has been exploited for the study of entanglement dynamics.The purpose of this paper is to study the entanglement properties of a system consisting of two isolated two-level atoms in their respective JC cavities.These two atoms do not interact but are entangled with each other.Each two-level atom is in a perfect single-mode resonator,but each is completely isolated from the other atom and the other cavity.We found that the entanglement dynamics of the two atoms are related to the initial entanglement magnitude between the two atoms and the atomcavity coupling strengths.Besides,the sudden death and rebirth of entanglement can also appear under some initial conditions.

The structure of this paper is as follows.In section 2,we introduce the physical model and derive the basic equations for entanglement dynamics.In section 3,we perform a detailed investigation of the time evolution of the quantum entanglement of two JC atoms for the case of initial Bell-like states.Finally,we conclude this work in section 4.

2.The model and basic equations

In this section,we consider a system consisting of the double JC model,as schematically shown in figure 1.The Hamiltonian of the system can be described by [18-20](ħ=1)

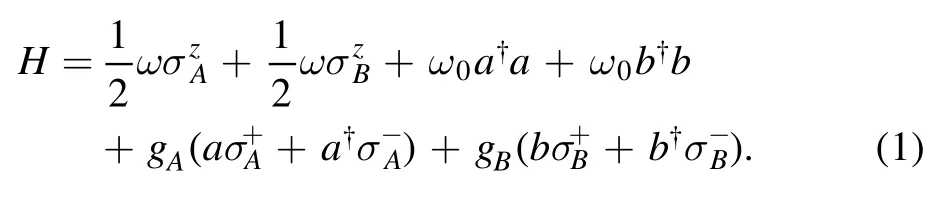
Here,ω0is the frequency of single-mode cavities a and b,ω is the transition frequency of the two-level atoms A and B,gA(gB) is the coupling strength between the atom A(B) and optical cavity a(b),are the atomic Pauli z-operator,the raising operator,and the lowering operator,respectively,for atom α=A,B,and a (b) and a†(b†) are the annihilation and creation operators for cavity a(b).

Because the atoms only interact with their own cavities,the eigenstates of this total Hamiltonian are the products of the dressed eigenstates of the separate JC systems [18-20].Note that the total excitation number N=NA+ NBis conserved,whereandare the excitation numbers of the first and second JC models.We now consider that the total excitation number is one(N=1),and there are only two categories of eigenstates.The first is where excitation exists in the first JC system and the other JC system is in the ground state i.e.NA=1,NB=0.The second type is where excitation is present in the second JC system,with NA=0,and NB=1.Under the resonance condition and with ω=ω0,the four eigenstates and eigenvalues in the interaction picture are as follows [21,22]:

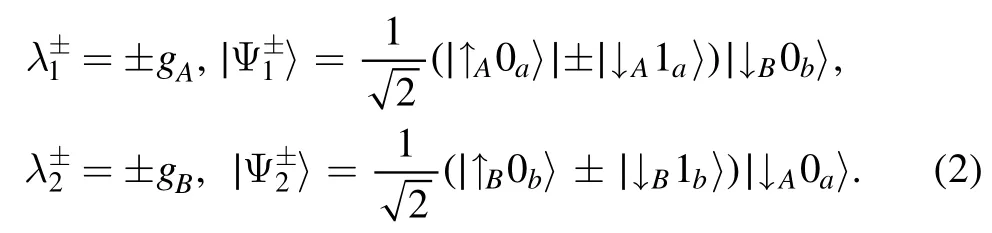
In the following,the states are abbreviated as∣ABab〉 with A,B=↑ or↓ ,and a,b=0 or 1.The bare basis can then be rewritten asin the single-excitation subspace.In the subspace,the state at any time reads

with the initial condition {x0,y0,z0,k0}.Inserting equations (1) and (3) into the Schrödinger equation,the time derivative of the coefficient can be obtained as

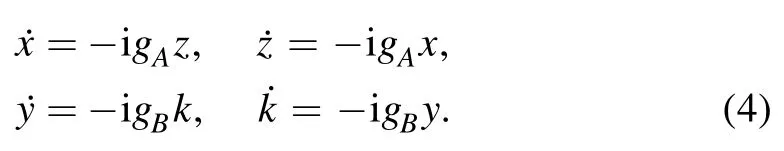
We note that x and z form a closed equation system,and the same is true for y and k.This is because there is no interaction between the two JC models.Thus,the coefficients can be derived as the following time-dependent formulas,

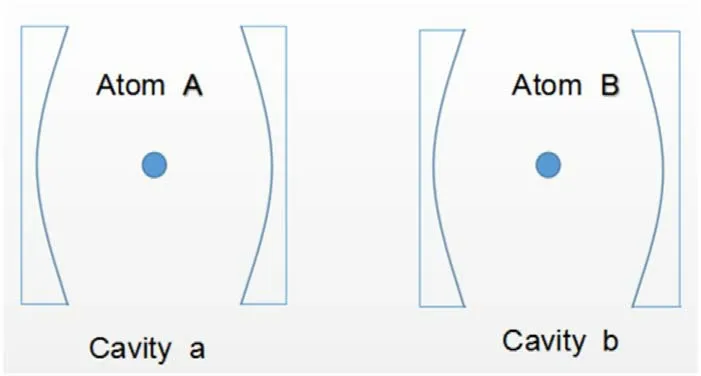
Figure 1.The double Jaynes-Cummings model consists of two atoms in their own perfect single-mode resonator cavities.These two atoms does not interact but are entangled with each other.Each twolevel atom is completely isolated from the other atom and the other cavity.

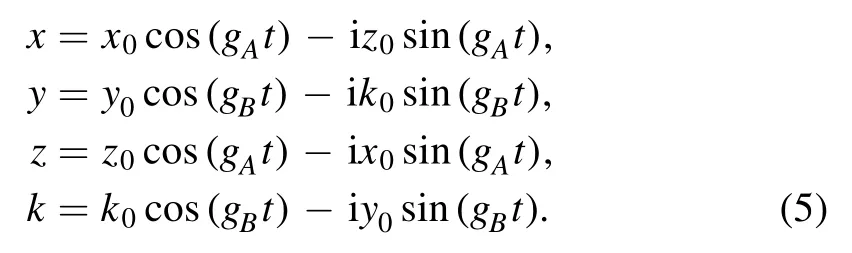
From equations (2)-(5),we can see that there must be only one independent JC model that evolves over time,while the other is in the ground state∣↓0〉 .

The entanglement information between the two atoms is contained in the reduced density matrix ρAB.It can be obtained by tracing out the photonic parts of the total pure state in equation (3).The reduced density matrix ρABin the basisis given by

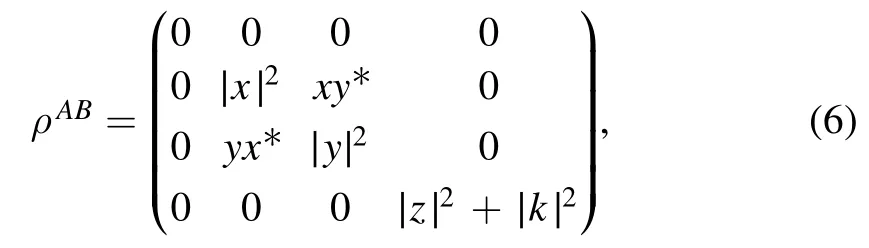
which is an X-type matrix.We use concurrence to measure the entanglement between the two atoms [23].It is obtained as

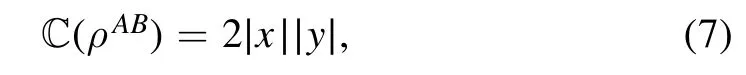
where the time-dependent probability amplitudes read

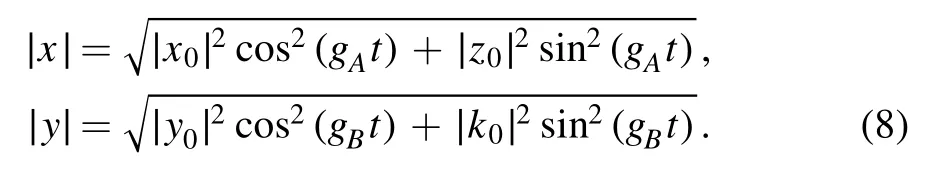
As all subsystems are two-state systems in the subspace,the following six kinds of entanglement between two qubits can all be derived: CAB,Cab,CAa,CBb,CAb,and CBa.There are some relations between these concurrence [24],but we confine our attention to CAB.

3.The case with initial Bell-like states

In the case of two initial zero coefficients,the two subsystems are initially entangled,while the other two subsystems are separable.In principle,there are six possibilities for two coefficients to be zero.These initial states can be expressed as the superpositions of two subsystem Bell states:∣10〉 ± ∣01〉 ,～ ∣↑0〉 ± ∣↓1〉,respectively.Here,we denote the superposition states within each type as follows:

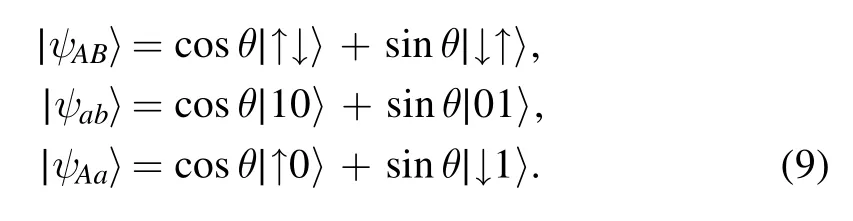
Although six different kinds of bipartite entanglements may arise,we will mainly study the entanglement dynamics of two JC atoms with different initial states; we find that among the six different initial states,two kinds of initial state,∣ψAa〉 and∣ψBb〉 ,need not be considered.

3.1.Partially entangled Bell states |ψAB〉 or |ψab〉

In this subsection,we take the partially entangled Bell states∣ψAB〉 or∣ψab〉 as our initial states.The initial states for the total system read:

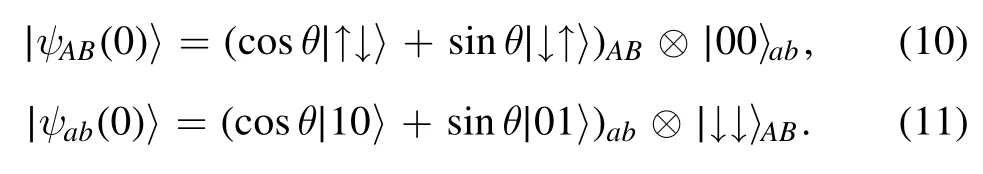
In both cases,the concurrence between atoms is

whereQα β(t)has the following expression for its initial state∣ψαβ(0) 〉:

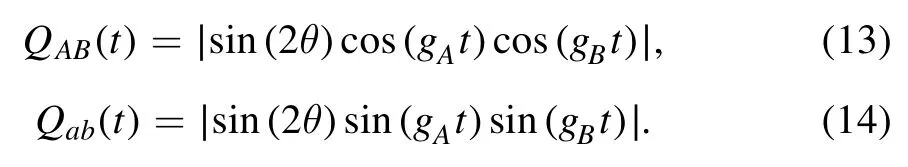
It can clearly be seen that the concurrence dynamics between two JC atoms are determined by the initial-state parameter,θ,and the coupling strengths gAand gB.

In figure 2,we plot the dynamics of concurrence CABagainst different values of the initial-state parameter,θ,and the coupling strengths gAand gB,for the initial states∣ψAB(0)〉equal to half of the Rabi periodicity and∣ψab(0)〉.We can see that the zero-concurrence moments depend on the coupling strengths gAand gB.As we all know,the information in each JC cavity is transferred from the atom to the optical cavity,i.e.,| ↑ 〉ito |1〉i,which takes a timeWhen the zero point of entanglement occurs,there must be at least one JC system that has completed this transform.What is more,a comparison of all the subgraphs in figure 2 shows that the greater the ratio of the coupling strengths,the more the entanglement concurrence fluctuates.These conclusions are consistent with Yonac’s work [20,22].

In figure 2,when the initial state is∣ψab(0)〉in equation (13),at the initial moment,two JC atoms are in the ground state and are separable.Then,with time,energy is transmitted periodically between the atoms and light fields in the JC models.CABstarts from zero and increases to the maximum value,and then collapses and revives.What is more,the conclusions regarding periodicity are the same as those in figure 2.If two Rabi periods are rational,a periodic change of atomic entanglement exists.Otherwise,the periodic phenomenon in the atomic entanglement dynamics vanishes.

We now focus on the periodicity of concurrence dynamics.The ratio of the coupling strengths takes the value ofin figures 2(a),(b),in figures 2(e),(f),andin figures 2(c),(d).Observing figures 2(c) and (d),the most obvious difference from other subgraphs is that the collapse and revival of concurrence is no longer periodic.This phenomenon can be explained from a physical perspective.Only under the transformations∣↑↓ 00〉 → ∣↓↓ 10〉 → ∣↑↓ 00〉and∣↓↑ 00〉 → ∣↓↓ 01〉 → ∣↓↑ 00〉 does the state remain unchanged.This conversion takes a time which is the least common multiple of two Rabi cycles,i.e.,with integers kAand kB.This means that the evolutionary periodicity of CABcan only be found when the ratio of the two coupling strengths is a rational numberOtherwise,there is no period in the time evolution of the concurrence.

Besides,the physical mechanism of concurrence dynamics can also be understood from the perspective of energy transfer.For the initial state∣ψAB(0)〉,the energy is distributed in the two atoms at the initial moment,and the entanglement information takes a maximum value of sin (2θ).With the energy transfer from atoms to the light fields,the entanglement between the two atoms is then destroyed.In a cycle,the number of zero-entanglement occurrences is determined by the ratio of the two coupling strengths.When the ratiois odd,there will be n entangled zeros,while when n is even,there are n + 1 zeros.

Naturally,one might wish to compare the entanglement dynamics for two different initial states,∣ψAB(0)〉and∣ψab(0)〉.As shown in figure 3,when the ratio of the coupling strengths is odd,concurrence with these two initial states only differs by a phase ofas shown in figures 3(c) and (d).However,figures 3(a) and (b) show that the entanglement with these two initial states does not coincide after a simple time translation.This is because the ratio of the evolution periods in the two cavities is even.In this case,the energy of one JC model is already distributed within the light field,but the energy of the other JC model is distributed in the atom.Thus,there is no way to overlap by shifting phase by

3.2.Partially entangled Bell states |ψAb〉 or |ψBa〉

In this subsection,we will further analyze the cases with initial states∣ψAb〉 and∣ψBa〉 .The initial states of the total composite system are

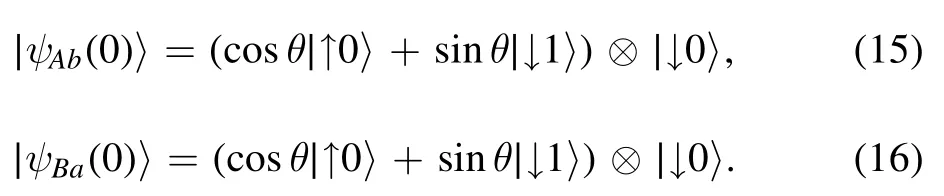
Similarly to the previous subsection,we also defineQ Ab(t)andQ Ba(t)as the concurrence of two atoms with initial states of∣ψAb〉 and∣ψBa〉 ,respectively,

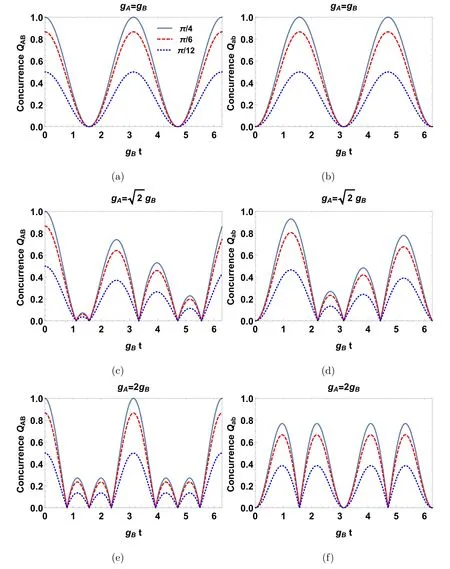
Figure 2.Figures(a),(c),and(e)show the evolution of the functionQ AB (t)for the concurrence of two atoms over time when the initial state is∣ψAB (0)〉,and(b),(d),and(f)expressQ ab (t)when the initial state is∣ψab (0)〉.The ratio of the coupling strengths takes a value ofin subgraphs (a) and (b)in subgraphs (c) and (d),and subgraphs (e) and (f).In both subgraphs,the gray-blue solid lines represent the initial-state parameter the red dashed lines representand the blue dotted lines represent

Figure 3.A comparison of the atomic concurrence,CAB,with two different kinds of initial state.The gray-blue solid lines shows the evolution process of the concurrence for the initial state∣ψAB (0)〉,while the red dashed lines depict the case for the initial state∣ψab (0)〉.The initial-state parameter,θ,is fixed at in all subgraphs.In subgraphs(a)and(c),the ratios of the coupling strengths ake values of 2 and 3,respectively.Subgraphs (b) and (d) are a comparison betweenQ ab (gt)andQ AB (gt)after shifting the phase to the left by

Figure 4.The dynamics of concurrenceCAB for(a)an initial state of∣ψAb (0)〉and(b)∣ψBa (0)〉.In images(a)and(b),the gray-blue solid line,the red dotted line and the blue dotted line are respectively used to indicate that the ratios of coupling intensity of the two cavities are 1,and 2.The initial-state parameter,θ,is fixed at in all subgraphs.

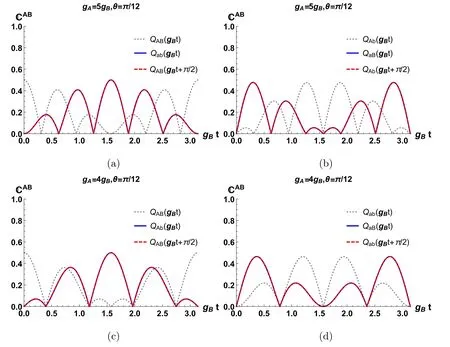
Figure 5.A comparison of entanglement dynamics for four different initial states.The superscript Qαβ indicates the case for the initial state∣ψαβ (0) 〉.The ratio of the coupling strengths takes a value of 5in subgraphs (a) and (b),and 4in subgraphs (c) and (d).In all subgraphs,the initial-state parameter,θ,is fixed at

Figure 4 shows the entanglement dynamics between atoms for initial states∣ψAb(0)〉and∣ψBa(0)〉.We can see that the periodicity depends on the rationality of the ratio of the two coupling strengths.In addition,the determination of whether the maximum value can reach 1 is made by the initial parameters and the ratio of the two coupling strengths.

In figure 5,the answer to whether there is time translation between these two kinds of initial state,∣ψAb(0)〉and∣ψBa(0)〉,depends on odd versus even numbers of the coupling-strength ratio.Another interesting conclusion can be obtained by comparing the four different initial states above.When the ratio of the two coupling strengthsandbut when the ratiois even,and

4.Conclusions

We studied the entanglement dynamics of two atoms in the double JC model.The two atoms were coupled to their single-mode optical cavities,and the two JC models were isolated from each other.In the single-excitation subspace,the double JC model can be equivalent to a four-qubit system.In this paper,we used concurrence to measure atomic entanglement and considered initial states to be Belllike states.We demonstrated that collapse and revival exist in entanglement dynamics.The physical mechanism behind the entanglement dynamics is the periodic information and energy exchange between atoms and light fields.Besides,for initial Bell-like states,the evolutionary cycle of the atomic entanglement can only be found if the ratio of the two atom-cavity coupling strengths is a rational number.Also,the existence of time translation between two kinds of initial Bell-like state depends on odd versus even numbers of the coupling-strength ratio.In summary,our results reveal the detailed dynamic evolution of two-body entanglement in the double JC model.We will study entanglement dynamics further in the multi-excitation space(which can make the light field contain two or more photons),to observe the phenomenon of sudden entanglement.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grants No.11935006,11975095,12075082,11947081 and 11847010),the Hunan Provincial Natural Science Foundation of China(Grant Nos.2019JJ50007),the Science Foundation of Hengyang Normal University (Grant No.17D18),and the Hunan Normal University Open Foundation of the Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of the Ministry of Education(Grants Nos.QSQC2008).