Curvature-induced noncommutativity of two different components of momentum for a particle on a hypersurface

Z Li,X Yang and Q H Liu,3

1 School for Theoretical Physics,School of Physics and Electronics,Hunan University,Changsha 410082,China

2 School of Materials Science and Engineering,Guilin University of Electronic Technology,Guilin,541004,China

3 Synergetic Innovation Center for Quantum Effects and Applications (SICQEA),Hunan Normal University,Changsha 410081,China

Abstract As a nonrelativistic particle constrained to remain on an (N-1)-dimensional ((N ≥2))hypersurface embedded in an N-dimensional Euclidean space,two different components pi and pj(i,j=1,2,3,…N)of the Cartesian momentum of the particle are not mutually commutative,and explicitly commutation relationsdepend on products of positions and momenta in uncontrollable ways.The generalized Dupin indicatrix of the hypersurface,a local analysis technique,is utilized to explore the dependence of the noncommutativity on the curvatures around a local point of the hypersurface.The first finding is that the noncommutativity can be grouped into two categories; one is the product of a sectional curvature and the angular momentum,and another is the product of a principal curvature and the momentum.The second finding is that,for a small circle lying a tangential plane covering the local point,the noncommutativity leads to a rotation operator and the amount of the rotation is an angle anholonomy; and along each of the normal sectional curves centering the given point the noncommutativity leads to a translation plus an additional rotation and the amount of the rotation is one half of the tangential angle change of the arc.

Keywords: constrained motion,quantization,hypersurface,Dirac brackets,geometric momentum

1.Introduction

In quantum mechanics there are so-called fundamental quantum conditions that include as the vital part the commutation relations between any pair of different components of momentum [1,2].The momentum operators in flat space are well understood,but it is not so in a curved space or on a curved hypersurface.Dirac presented in 1950[2]a highly theoretically satisfactory procedure of constructing the commutation relations for momentum for constrained motions [2-4],and the commutation relations for momentum can be easily constructed.However,the commutation relations have complicated structure due to the operatorordering problem,so the decipherment of the structure is crucial in exploration of the surface quantum states in,for instance,surface plasmon polaritons,topological insulators,carbon nanotubes and fullerenes,etc.It is therefore an important issue to get the definite meaning of the commutation relations for momentum for a particle constrained on the curved hypersurface,which attracts constant interests [5-12].Recently,we proposed a geometric momentum [12-21] which is the solution of the commutation relations.In present paper,we try to understand the commutation relations around a local point on the curved hypersurface.

The local analysis technique is powerful tool in physics and mathematics in dealing with complicated theoretical structure.For instance,the small region of globally curved spacetime is approximately flat,and a non-linear differential equation can be made a linear one if examined locally.For a two-dimensional curved surface,the Dupin indicatrix is a standard method for characterizing the local shape of a surface [22],which can be easily to be generalized to hypersurfaces in higher dimensions to analyze the local shape[23].Such an analysis was performed to investigate the curvatureinduced potential for the particle constrained on the hypersurface [10],yielding a form of the curvature-induced potential originally predicted by the well-defined confining potential formalism [24] (or called thin-layer quantization procedure [10]).In present study,the technique is utilized to investigate the long-lasting noncommutative commutation relations of momentum operators,revealing novel results.

For a nonrelativistic particle constrained to remain on an(N-1)-dimensional smooth curved surface ΣN-1in flat space RN(N≥2),one can for the particle define N pairs of Cartesian variable(pi,xi) (hereafter i,j,l=1,2,3,… N)where piis ith Cartesian momentum and xiis ith coordinate.To note that the surface ΣN-1has only N-1 local independent coordinates,and the N Cartesian coordinates xiare determined by the surface equation,f(x1,x2,…,xN) =0,say.In Dirac’s classification scheme,hypersurface constraints belong to the second-class [1,4,11],and Dirac gave a standard procedure to deal with it in both classical and quantum mechanics.The key quantity is the so-called Dirac bracket[A,B]Din his honor instead of the usual Poisson one[A,B]for the two functions A and B depending on variables xiand pi[1,4,11],

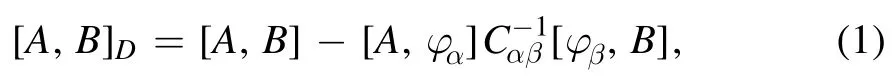
whereCαβ≡[φα,φβ] are the matrix elements in the constraint matrix and the functions φαare constraints,and one can refer a recent textbook [11] for details.It has been long known that two different components of the momentumpdo not commute with each other [5-11]

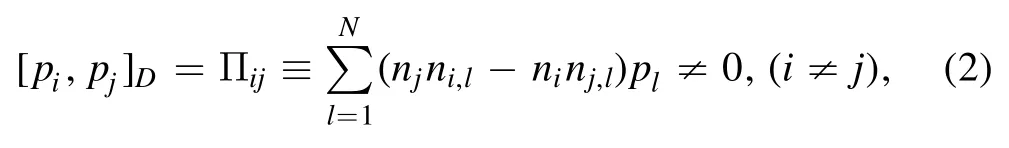
where niis the ith component of the normal vectornat a point of the surface ΣN-1and symbol‘,l’in the subscript stands for the derivative with respect to the coordinate xl,and so forth.

For the constrained motion,the usual canonical commutation relations are hypothesized to be given by

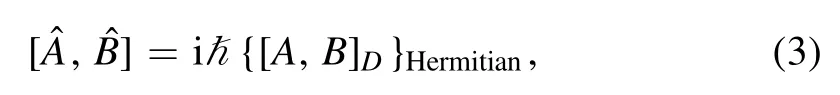
where OHermitianstands for a Hermitian operator of an observable O [1,4,11].Thus we can construct the quantum mechanical commutation relations for momentum

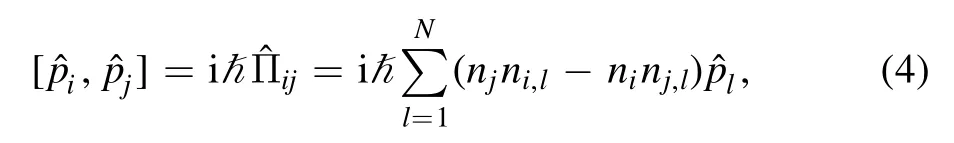
wheredenotes the operator form of a classical quantity F.A notoriously operator-ordering difficulty as to distributein njni,land ninj,lin(4) is hard to resolve [26].Take the distribution problem of insertingin njni,lfor instance,and there are different approaches.The first approach is a simple combination of two possibilitiesand[6],and the second is to consider following four possibilitiesand[7].However,the attempt of Weinberg is different,and he insertsinto position-dependent factors forming nj[11].So far,except for very special case such as the spherical surface [5-15] and the flat plane,the physical significance of the quantity(4) in general has been an open problem for quite a long time,at least since 1990[6-11].Another important issue relevant to a nonrelativistic particle constrained on the hypersurface is that there is the curvature-induced geometric potential [13,20,25],but in present paper we deal with fundamental quantum conditions (4) which apply to both nonrelativistic and relativistic case.

2.A local expansion of the surface equation and noncommutativity without operator-ordering problem

Let us consider the surface equation f(x)=0,where f(x) is some smooth function of positionx= (x1,x2,…xN) in RN,whose normal vector isWe can always choose the equation of the surface such thatso thatn≡∇f(x).This is because physics does not depend on the specific form of the surface equations,but depend on the invariants of the surface.Some geometric invariants include,the normal vector,principal curvatures,and number of genus,etc.At any point of the surface,let us attach an N-dimensional Cartesian coordinates at it and locate the origin O at the point.In a sufficiently small region covering the origin O,we construct a system of orthogonal coordinates (X1,X2,…XN-1,XN) which can be used to specify a point in the vicinity of the origin O(X=0) on the hypersurface,and the surface equation around the origin O can be so chosenf(X) ≡XN-w(X1,X2,…XN-1)thatw(X1,X2,…XN-1) is Monge’s form of the hypersurface.What is more,we can always choose the coordinates such that the normal directionnis along the XN-axis and principal directions are along N-1 coordinates Xa(a,b=1,2,3,…N-1),respectively.Now the orthogonal coordinates(X1,X2,…XN-1,XN) is the orthogonal frame of the surface,and the hypersurface is asymptotically represented by the generalization of the two-dimensional Dupin indicatrix [10,22,23]

where kais the ath principal curvature of the curve formed by the intersection of theX a XN-plane on the hypersurface ΣN-1at the origin O,and the intersections from the normal sections,and there are in total N-1 normal sections.The above equation ignores the higher order terms of Xaand the formula holds up to the second order.A productKab≡k a kb(a≠b)is right the abth sectional curvature [10,27,28].The normal vector near the origin O is,

which at O reduces ton= (0 ,0,… ,0,1).The derivative of the normal vectornwith respect to the coordinate Xlgives,

where o(X) and o(X2) denote quantities of order X and X2,respectively.At O,we have,respectively,the mean curvature,

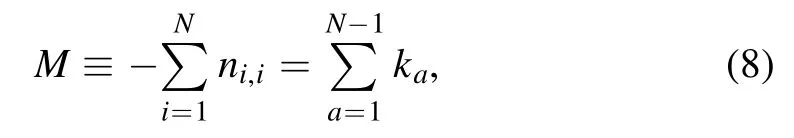
and,

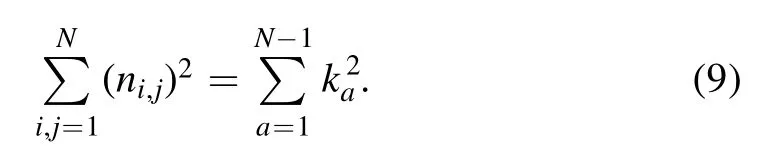
The central results of the present study are from equations (6b)to (7),up to the leading term,

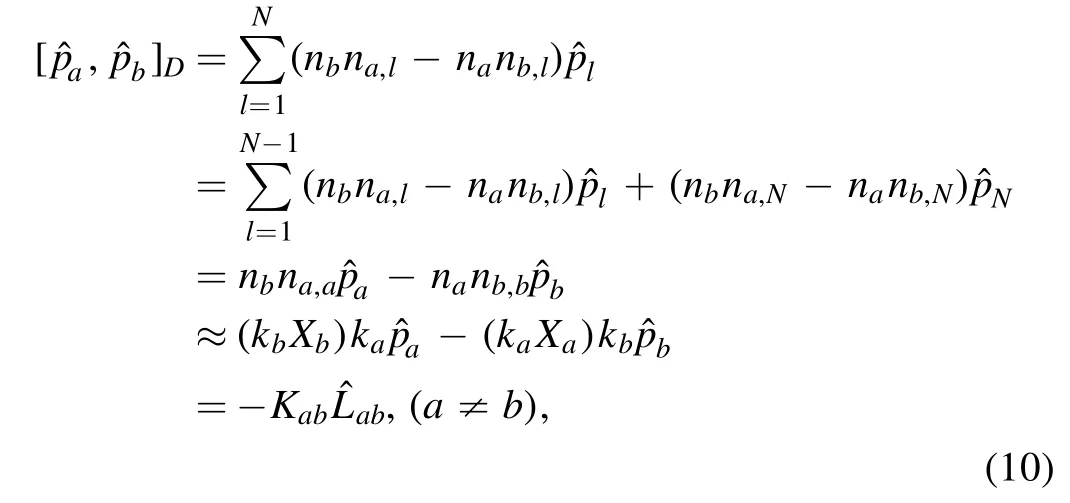
whereLab≡X a pb-Xb pa,and,

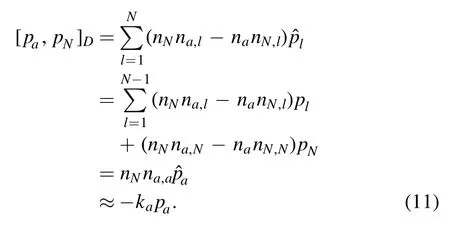
In consequence,we have the local commutation relations,

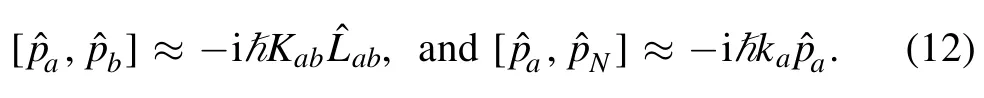
These two sets of commutation relations are remarkable for they are free from operator-ordering difficulty.

Two immediate remarks on these local relations (12) follow.(1) They depend on the local geometric invariants of the surface such as Kab,ka,andetc,so they hold irrespective of coordinates chosen.(2)The brackets(10)and(11)are zero once Kaband kaare zero respectively,as expected.

3.GIDOs and rotations

Now we further investigate the physical significances of the commutation relations (12).

First,we construct a GIDO along a small circle which is approximated by a small square in the tangential XaXb-plane around the origin O; and let the small square be formed by four points atandwith center at the origin O with∣dXa∣=∣dXb∣.The initial and final points of the displacements coincide at pointand order of the displacement is M → N → I → P → M .We have a GIDO along a small square □MNIP,

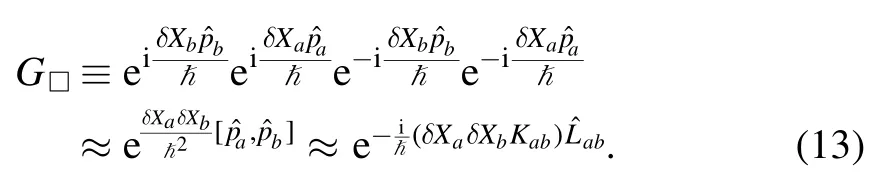
In calculation,the Baker-Campbell-Hausdorff formula for two possibly noncommutative operators u and v asis used.We see that the GIDO G□(13)is a rotational operator on the XaXb-plane,and the angle of the rotation iswhich is the sectional anholonomy.It is originally defined by the angle of rotation of the vector as it is accumulated during parallel transport of the vector on a the hypersurface along the small circle on the XaXb-plane.The angle anholonomy formed by a loop covering an finite area ΔS on the hypersurface is given by

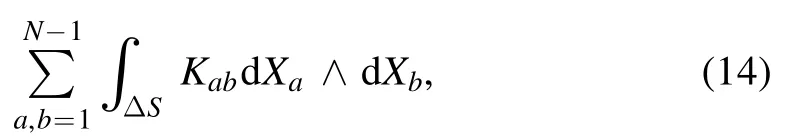
where the finite area ΔS is formed by infinitely many flat pieces covering the area,and2πχ,where χ is the Chern number.

If the hypersurface is a two-dimensional spherical surface,the angle anholonomy is equal to the solid angle subtended by loop.If the surface is locally a saddle,the infinitesimal angle anholonomy is negative.If it is a cylinder whose Gaussian curvature is vanishing,the angle anholonomy is zero.

Secondly,considering the small arc length from Evia O toalong the small portion of the normal sectional curve on the normalX a XN-plane at the origin,we immediately find that the commutatorleads to a displacement plus an additional rotation.To see it,we construct following GIDO which shifts a quantum state along the arc from point E → O → G,

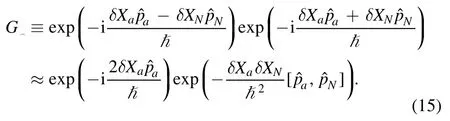
In right-handed side of this equation,we see two parts,and one is a simple translational operatorand another is,

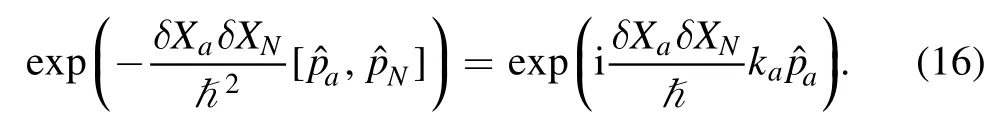
The physical significance becomes evident.The arc length element of along E → O → G iswith noting thatfrom (5),which is ignorable in comparison withThe change of the tangential vector along the arc isand we have from above equation (16)

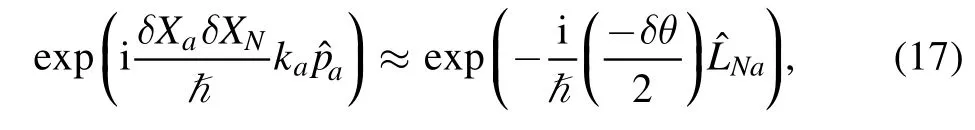
where an angular momentum operator defined by a torque of momentumwith respective to point (0,-) is

Let us move a quantum state along closed curves formed by piecewise smooth normal sectional lines,the rotation operator gives an accumulation of the rotational angle isSpecially,when the surface is a two-dimensional spherical surface,the normal sectional curves are great circles and the GIDOG^for a great circle leads to that the total angular change is 2π.

Thus,we have demonstrated that two seemingly different kinds of noncommutativity,given by (12),have the same crucial parts:rotation operators given by G□(13)and(17)inG^(15),respectively.The amount of the rotations depends on the curvature of the surface.

4.Conclusions and discussions

For a nonrelativistic particle constrained to remain on a hypersurface,Dirac brackets for two different components of momentum are not mutually commuting with each other.The noncommutativity Πijon a local point of the hypersurface is examined and results show that the noncommutativity is due to the local curvature of the surface.At the point,there are,respectively,mutually perpendicular twodimensional tangential planes and N-1 mutually perpendicular normal sectional curves.In quantum mechanics,with GIDOs constructed on the base of the noncommutativity,we find that,at the point,for a small circle lying on each of the tangential planes covering the point the noncommutativity leads to a rotation operator and the amount of the rotation is an angle anholonomy,and for a short arc length along each of the intersecting curves centering the given point the noncommutativity leads to a translation plus an additional rotation and the amount of the rotation is one half of the tangential angle change of the arc.All results are obtained by examination of the noncommutativity,without necessarily knowing the explicit form of the momentum.

In many aspects our results are in sharp contrast to what the intuition suggests.For instance,the locally approximated flatness of the surface suggests that the momentum might reduce to the usual one,but it is not the case for that the noncommutativity depends on the curvature.The noncommutativity of commutation relations for momentum operators on a local point remains,but the heavy operatorordering difficulty is got rid of.There is no angular momentum operator in the commutation relationsbut they can certainly have quantum states on the surface angularly shifted.

Acknowledgments

This work is financially supported by National Natural Science Foundation of China under Grant No.11 675 051.

ORCID iDs