钢筋混凝土结构正截面承载力统一算法研究

张 泉

[上海市政工程设计研究总院（集团）有限公司，上海市200092]

0 引 言

现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）（简称《规范》）第5.2～5.4条文，针对不同受力状态，规定了钢筋混凝土结构正截面承载力算法，并且规定在计算分析时应首先区分受力状态，确定适用规范条文后再进行计算。

在不同计算工况下，同一个计算截面可能会有不同的受力状态，若根据受力状态分情况计算，则计算过程相当繁琐。《规范》算法适用较规则截面，如矩形、T 形、I 形、圆形，当遇到不规则截面时就不能直接计算。为解决这些问题，曾有研究者由基本计算假定出发，根据材料的本构关系推导出钢筋混凝土结构在不同受力状态下的正截面承载力统一算法[1]。

1 现行规范算法

根据《规范》第5.2～5.4 条文规定，不同受力状态下钢筋混凝土结构正截面承载力计算公式如下所示：

（1）对于矩形截面受弯构件：

式中：γ0为结构重要性系数；Md为弯矩设计值；fcd为混凝土轴心抗压强度设计值；b为截面宽度；x为截面受压区高度；f"sd为普通钢筋受压强度设计值；为受压区普通钢筋截面面积；h0为截面有效高度；a"s为受压区普通钢筋合力点至受压区边缘距离；f"pd为预应力钢筋受压强度设计值；σ"p0为受压区预应力钢筋合力点处混凝土法向应力等于零时预应力钢筋的应力；A"p为受压区纵向预应力钢筋截面面积；a"p为受压区预应力钢筋合力点至受压区边缘距离。

（2）对于轴心受压构件：

式中：Nd为轴向力设计值；φ 为轴压构件稳定系数；A为轴压构件毛截面面积。

（3）对于矩形截面偏心受压构件：

式中：σs为截面受拉边纵向钢筋应力；As为截面受拉边纵向钢筋截面积；e为轴向力作用点至受拉边或受压较小边纵向钢筋合力点的距离。

采用规范条文对偏心受压构件进行验算时，式（3）、式（4）需同时满足。式（3）用于验算截面轴力，式（4）用于验算截面弯矩。下述偏心受拉构件的验算与此同理。

（4）对于轴心受拉构件：

式中：Nud为构件截面轴心受拉承载力；fpd为预应力钢筋受拉强度设计值；Ap为预应力钢筋截面积；fsd为普通钢筋受拉强度设计值。

（5）对于矩形截面偏心受拉构件：

a. 小偏心受拉构件：

式中：e" 为轴拉力距受拉较小侧钢筋合力点距离；为受拉较小侧截面有效高度；as为受拉较大侧普通钢筋合力中心距截面边缘距离；ap为受拉较大侧预应力钢筋合力中心距截面边缘距离。

式（6）、式（7）的适用条件与式（3）、式（4）相同。

b. 大偏心受拉构件：

除上述公式之外，还有一些适用于特定情况的计算公式，详见《规范》。

2 计算假定

根据《规范》第5.1.3 条规定，构件正截面承载力计算应满足以下假定[3]：

（1）构件弯曲后，其截面仍保持平面。

（2）截面受拉混凝土的抗拉强度不予考虑。

（3）纵向体内钢筋的应力等于钢筋应变与其弹性模量的乘积。

另外，因本文讨论钢筋混凝土构件，补充如下约定：截面无预应力钢筋及预应力钢束布置。

3 材料本构关系

根据《混凝土结构设计规范》[2]第6.2.1 条规定，取混凝土及钢筋材料本构关系如下[4]。

（1）对于混凝土材料：

式中：σc为截面混凝土应力；fc为混凝土抗压强度设计值；εc为截面混凝土应变；ε0为混凝土压应力达到fc时的压应变，ε0=0.002+0.5（fcu，k-50）×10-5；εcu为混凝土极限压应变，εcu=0.003 3-（fcu，k-50）×10-5，其中 的fcu，k为混凝土立方体抗压强度标准值，fcu，k≥50；n=2.0-（fcu，k-50）/60。

混凝土材料本构关系见图1，图中σ 为混凝土应力。

（2）对于钢筋材料：

图1 混凝土本构关系

式中：fy为钢筋抗压强度设计值；其余参数含义见《规范》。

钢筋材料本构关系见图2。

图2 钢筋本构关系

4 计算理论

4.1 承载力计算

根据《混凝土结构设计规范》[2]E.0.1 计算理论，以外力作用点为原点计算混凝土截面的应力积分，并叠加所有钢筋在原点处的内力计算值作为截面抗力，分别列出Nx、My、Mz内力平衡方程，得出截面极限承载力。截面形状及内力示意图见图3；截面应力和应变分布见图4。

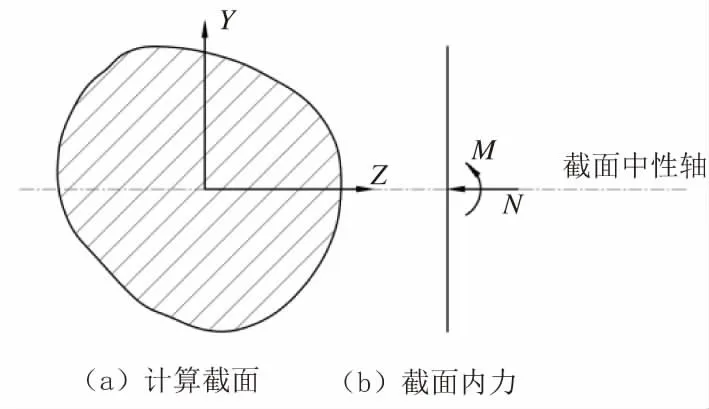
图3 截面形状及内力示意图

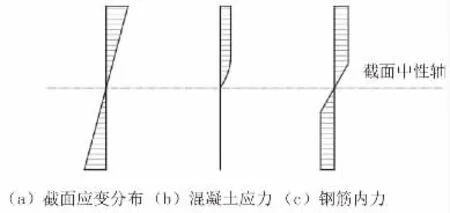
图4 截面应力和应变分布

极限承载力Nxu、Myu、Mzu计算式为：

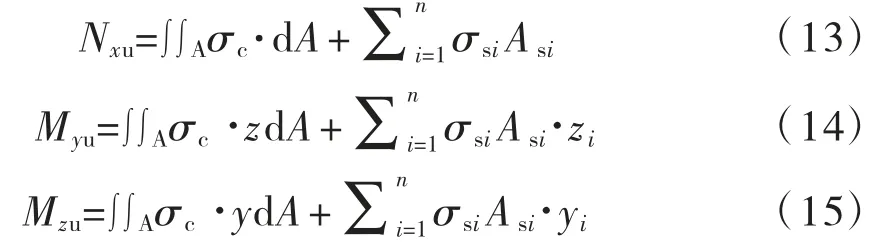
式中：dA为混凝土积分面积微元；σsi为第i根钢筋应力；Asi为第i根钢筋截面积；z为混凝土积分面积微元中心z向坐标；zi为第i根钢筋中心z向坐标；y为混凝土积分面积微元中心y向坐标；yi为第i根钢筋中心y向坐标。

对任意形状的混凝土截面，作用荷载（Nx、My、Mz），对双向弯矩进行合成计算如下：

式中：M为单向偏心受压计算截面弯矩。

同时旋转截面，使M方向指向z轴负向，如图3所示，则可将双向偏心受力构件转换为单向偏心受力构件。

此时，承载力计算公式为式（13）、式（15）。

计算承载力时，按等偏心距原则确定极限状态，即：

4.2 混凝土截面应力积分计算

4.2.1 规范算法介绍

《混凝土结构设计规范》[2]E.0.1 中，将混凝土截面细分为多个面积微元，计算各面积微元中心点的应力，累加后作为整个截面的应力积分。

这种计算方法比较直观，容易操作，但其缺点为：

（1）计算精度与截面细分程度相关，若截面划分精细，则计算精度高，计算量大；截面划分粗糙，则计算精度低，计算量小。

（2）以面积微元中心点应力代替整个面积微元应力分布，会带来计算误差。

（3）计算过程中会出现大量不必要的重复计算。当2 个面积微元处于截面同一高度处，且应力应变相同时，仍需分别进行计算。

为解决以上问题，经过对规范算法的研究，提出分域积分算法来计算截面应力积分。

4.2.2 分域积分算法

假定混凝土截面为直边多边形，即边界线均由直线段构成。对于一般截面，其中的曲线段(圆、圆弧、样条曲线）均可细分转换为直线段，从而满足前述条件。

取任意一截面，假定y+ 区域受压，y- 区域受拉，其计算截面、截面应变和应力分布见图5。

由图5 可知，混凝土截面分为3 个区域：最大应力区A；梯度应力区B；受拉区C。

A 区域应力积分计算为：

图5 截面形状及应力应变分布

4.2.3 梯度区应力积分计算

设该区域边界有节点P1～Pn，其中Pi、Pi+1与Y轴构成梯形子域Bi，如图6 所示。

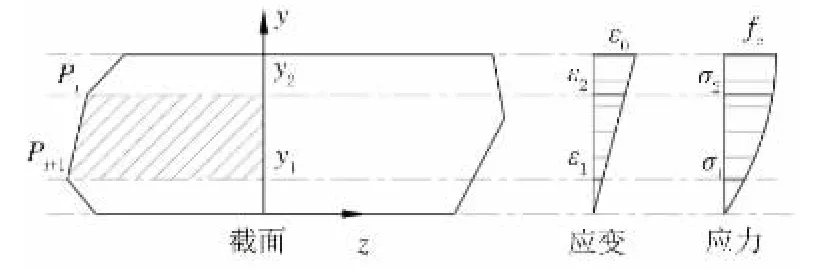
图6 梯度区及应力应变分布

遍历B 区所有边界节点，可形成子域B1～Bn，其中Bn的边界节点为Pn、P1。

设Pi坐标（z2，y2），Pi+1 坐标（z1，y1），计算Bi积分结果如下：

4.2.4 极限承载力计算

综合上述计算式，可得钢筋混凝土构件正截面极限承载力计算公式为：

4.3 关键参数计算

在以上计算过程中，给定中性轴位置及截面转角φ，可以得到1 组对应的承载力计算结果。

4.3.1 中性轴范围计算

设截面顶底缘钢筋位置分别为y1，y2，则中性轴位置上限的条件是：y1处钢筋应变为εsu，且y2处钢筋应变为εso；中性轴位置下限的条件是：y1处钢筋应变为εso，且y2处钢筋应变为εsu。则计算中性轴上下限位置如下所示：

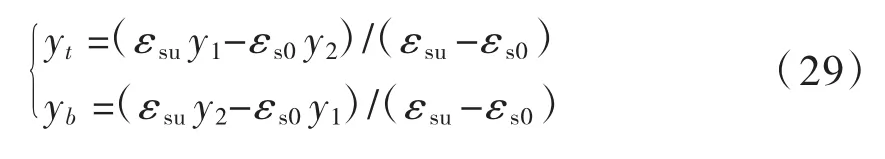
当中性轴在yb～yt之间变动时，截面承载力可以表现出轴心受拉、偏心受拉、偏心受压、受弯状态的特征，即偏心距e∈（-∞，+∞）。

4.3.2 截面转角计算

给定中性轴位置后，按如下原则确定极限承载状态下截面转角φ：

（1）受压侧混凝土最大应变为εcu。

（2）受压侧钢筋最大应变为-0.01。

（3）受拉侧钢筋最大应变为0.01。分别根据以上原则计算截面转角并取最小值作为计算参数φ。

4.3.3 中性轴位置计算

由于无法以解析形式直接得出中性轴位置，可以在（yb，yy）范围内以二分试算方式寻找中性轴位置。判别条件如下：

（1）Nxu与Nx方向相同；（2）计算出（Nxu，Mzu）与（Nx，Mz）偏心距一致，即满足式（17）条件。

5 计算中需注意的特殊情况

以上计算过程考虑钢筋混凝土构件的截面尺寸、材料特性、钢筋布置、本构关系、力学平衡等因素。另有一些特殊因素需考虑，在计算时应根据这些因素对计算结果进行修正。

5.1 不计入间接钢筋的轴心受压构件

根据《规范》第5.3.1 条规定，当不计间接钢筋作用时，轴心受压构件承载力按下式验算：

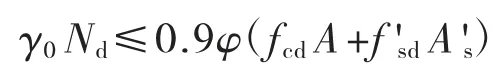
其中φ 为轴压构件稳定系数。

为使前述算法仍适用于轴心受压构件，对上式进行变形：

其中：fc=0.9φfcd；f"s=0.9φf"sd。

当作用荷载（Nx，My，Mz）时，My=0，Mz=0，且Nx为压力，可判别为轴心受压构件，应对混凝土及钢筋材料参数按式（30）修正，则得到的截面承载力满足《规范》第5.3.1 条要求。

5.2 计入间接钢筋的轴心受压构件

根据《规范》第5.3.2 条规定，轴心受压构件计入间接钢筋作用，需满足以下条件：

（1）钢筋混凝土构件；（2）圆形截面；（3）构件长细比l0/i≤48；（4）配置螺旋式或焊接环式间接钢筋；（5）间接钢筋换算截面积≥全部纵向钢筋截面积的25%；（6） 间接钢筋间距不大于80 mm 且不大于dcor/5。

由以上条件可看出，《规范》第5.3.2 条中的算法是针对一种特定构件的计算方法。因此，当遇到这种情况时，可直接按照《规范》第5.3.2 条中的公式计算。

5.3 高配筋率构件

在以上计算混凝土截面应力积分时，采用混凝土毛截面，未扣除钢筋面积。当构件配筋率较低（ρ≤1%）时，不会引起较大误差。随着配筋率提高，该误差将不断增大。

因此，对高配筋率构件（ρ＞1%），需对式（27）中钢筋内力计算项修正如下：

式中：σci为第i根钢筋中心处的混凝土应力。

6 计算结果对比

根据前述计算理论，以JAVA 1.8.0_191 实现计算过程。在程序中引入第三方工具包jts-1.14.jar，对直边平面域进行平移、旋转、剖切等操作。

选取空心板梁跨中截面如图7 所示。

图7 验算截面（单位：mm）

混凝土材料C40，材料参数如下：

钢筋材料HRB400，材料参数如下：

设构件的轴压构件稳定系数φ=0.81。

坐标原点设在截面中心，计算得：

计算如表1 所示工况下的构件承载力。

表1 中，轴力以压力为正，弯矩以y+ 区域受压为正。

将截面、材料、荷载信息输入《桥梁博士V3.5》[5]软件中计算，结果对比如表2 所示。

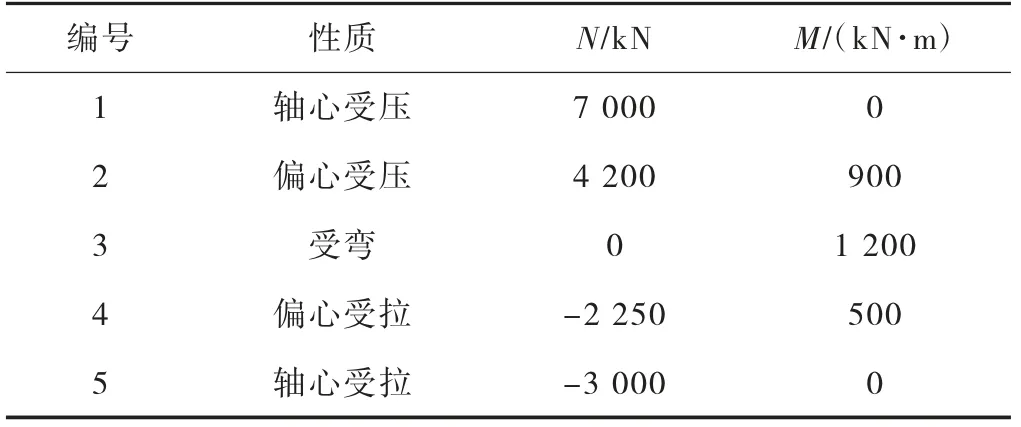
表1 计算工况

由表2 可看出，程序计算结果与《桥梁博士V3.5》计算结果一致，且程序计算结果略大于《桥梁博士V3.5》结果。原因是本文算法在计算混凝土域应力积分时采用分区积分算法，计算结果精度更高。

表2 计算结果对比

7 结 语

本文参考《混凝土结构设计规范（2015 年版）》（GB 50010—2010）E.0.1 中的计算方法，通过改进混凝土域应力积分算法，提出了钢筋混凝土构件截面承载力计算统一算法。该算法可适应任意受力状态、任意截面形状及配筋形式。

以JAVA 语言实现该算法，通过对一空心板截面进行计算并与《桥梁博士V3.5》计算结果对比，说明算法结果准确可靠。

该算法应用于桥梁设计工作，可提高工作效率，降低手算工作量，对设计工作有较大帮助。