曲线桥梁抗倾覆稳定参数分析
顾晓毅
[上海市政工程设计研究总院(集团)有限公司,上海市200092]
0 引 言
20 世纪90 年代以来,随着高速公路和城市立交桥建设日益增多,在高等级公路相交点或城市主干道交叉口的枢纽处,采用了大量曲线桥梁。曲线桥梁在力学特性上表现为竖向弯曲、面外变形与扭转的“耦合”,结构变形和受力复杂,因而设计时常采用闭口式箱梁截面,以利用结构的整体抗扭刚度。
值得注意的是,在桥梁墩位设置受限、桥梁曲率半径较小、跨度较大和施工条件困难等情况下,曲线桥梁常采用钢结构,以充分发挥钢结构工业化程度高、自重轻和便于现场安装等优点。与此同时,由于钢结构桥梁自重轻、活载和其他可变荷载比重大、日照梯度温度效应敏感等不利因素,导致近年来在桥梁施工和运营过程中,桥梁倾覆失稳事故常有发生,详见表1。
本文通过参数分析,从曲线桥梁支座布置、平面圆心角和曲率半径等方面,探讨曲线桥梁的抗倾覆稳定影响效应。
1 桥梁抗倾覆稳定设计准则
目前,国内桥梁规范关于桥梁抗倾覆稳定,考虑两个准则[1-3]:
(1)“准则一”:作用基本组合下,单向受压支座应始终保持受压状态;
(2)“准则二”:按作用标准组合时,作用效应应符合∑Sbk,i/∑Ssk,i≥Kqf(注:∑Sbk,i、∑Ssk,i分别为使结构稳定和失稳的效应设计值,抗倾覆稳定系数Kqf=2.5);
准则一考虑基本组合的可变荷载作用下支座不脱空,准则二考虑标准组合下支座对主梁绕某个不利主轴的扭转变形控制。两个准则互为补充。
国外规范对桥梁抗倾覆稳定的规定略有差异。英国《钢、混凝土结合桥规范》(BS5400)规定,对应标准荷载的最小恢复力矩应大于设计荷载的最大倾覆力矩(设计荷载分项系数1.5),相当于抗倾覆稳定系数Kqf=1.5;美国AASHTO《公路桥梁设计规范》针对抗倾覆稳定作了定性规定:结构作为一个整体和它的各构件应抵抗滑动、转动、提起和压屈荷载,分析和设计中应考虑荷载偏心矩对抗倾覆能力的影响。

表1 近年桥梁倾覆失稳事故
2 桥梁支座布置对抗倾覆稳定影响
桥梁的两端支座布置一般采用双支座,而中墩支座布置各有不同。可分为如图1 所示三种形式。

图1 曲线桥梁支座布置形式
理论研究表明,不同支座布置形式影响桥梁扭转受力,进而影响桥梁的抗倾覆性能。图2 为有限元参数分析结果曲线,反映了中墩分别采用单、双支座形式对桥梁抗倾覆稳定的影响,可以看出:中墩采用单支座布置时,抗倾覆稳定系数维持在较低水平,对桥梁平面半径不甚敏感;中墩采用双支座布置时,对桥梁抗倾覆稳定有利,Kqf随桥梁平面半径增大而显著提高。
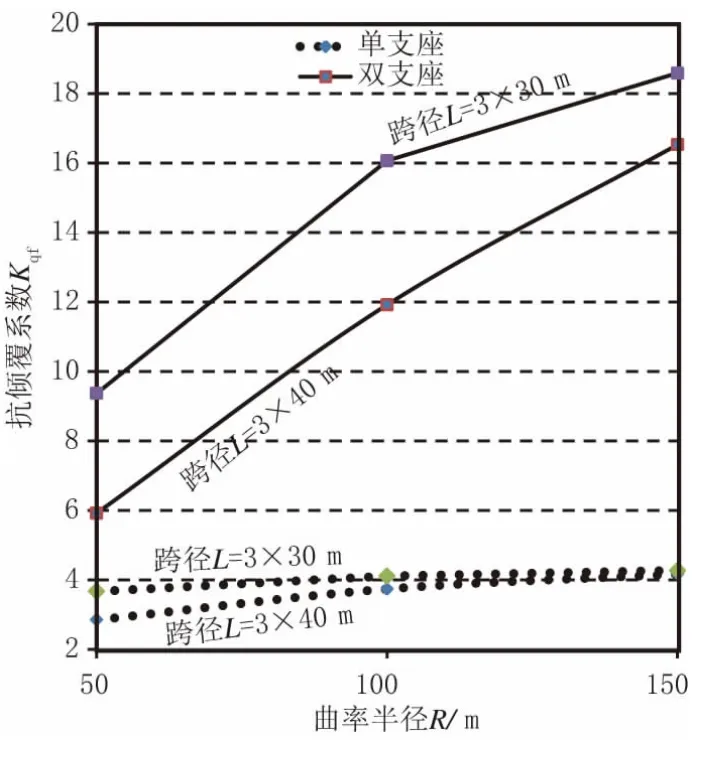
图2 单、双支座对抗倾覆稳定影响
为定量分析桥梁中墩在不同支座布置时,不同跨径和曲率半径的曲线桥梁Kqf和梁端内侧支座最小反力的变化情况,选取以下计算假定:
(1)荷载等级:城—A 级;
(2)桥梁结构采用宽度8.5 m、结构高度2.0 m的单箱室钢箱梁断面,梁端压重布置相同;
(3)双支座间距D=2.5 m,按恒载下内外侧支座反力均衡原则调偏;中墩单支座布置在结构中心线;
(4)抗倾覆稳定系数Kqf、梁端内侧支座最小反力N按国内规范[1-3]验算。
有限元参数分析结果曲线分别如图3、图4 所示。
图3 反映了基于“准则二”的抗倾覆系数Kqf变化规律:(1)相同跨径时,采用双支座布置的Kqf较大,单支座布置Kqf较小,单双支座间隔布置时在两者之间;(2)随着桥梁曲率半径增大,Kqf相应提高,同样跨径布置下,双支座布置时Kqf提高最为明显;(3)相同曲率半径时,Kqf随跨径布置增大而变小。
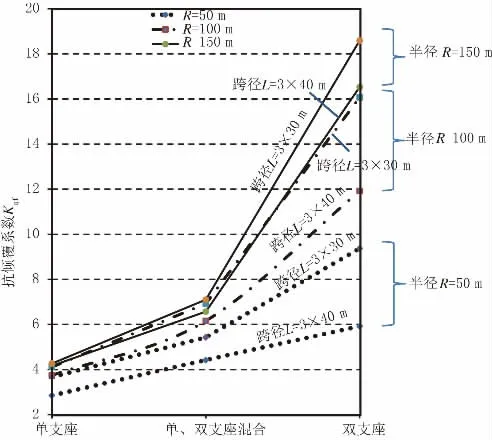
图3 抗倾覆稳定系数
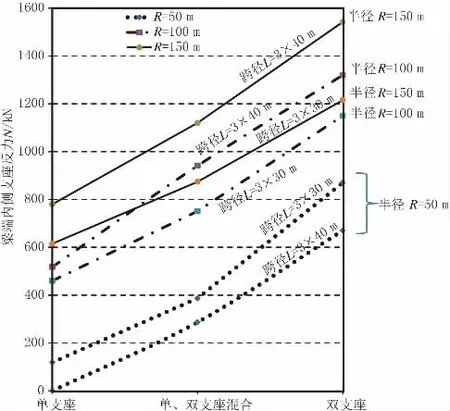
图4 主梁支座最小反力
图4 反映了基于“准则一”的梁端支座反力变化规律:(1)在桥梁同一跨径和曲率时,采用双支座布置时梁端支座反力储备N较大,单支座布置N较小,单双支座间隔布置N在两者之间;(2)同一跨径桥梁,随着桥梁曲率半径增大,梁端支座反力储备N显著增加;(3)桥梁曲率半径R较小时(如R=50 m),同样曲率半径下,当跨径布置增大时(即圆心角φ增大),由于受温度梯度内力影响,支座反力N反而变小。
由此可见,中墩采用抗扭双支座,可以有效改善曲线桥梁抗倾覆稳定性能,且Kqf随桥梁平面半径增大而显著提高。考虑到桥梁运营过程中公路超载或其他非预见性荷载常有发生,中墩尽可能采用双支座布置,这是提高桥梁抗倾覆能力的有效措施。
3 桥梁平面圆心角对抗倾覆稳定影响
曲线桥梁平面圆心角φ 是反映弯曲程度的重要参数,决定弯桥受力和抗倾覆稳定性。曲率半径相同时,一联桥梁的跨长越大,其弯曲程度越大,即扭转效应更为明显。有限元参数分析结果曲线图5 所示,反映了桥梁平面圆心角对桥梁扭转的影响,可以看到:圆心角φ 增大,曲线桥梁在抵抗扭转方面需要更大的抗扭力矩,对桥梁抗倾覆稳定影响更为明显。

图5 主梁恒载最大扭矩
图6 反映了基于“准则二”的中墩采用双支座的三跨钢梁Kqf—φ 变化规律:(1)随着圆心角φ 增大,桥梁抗倾覆稳定系数显著减少;(2)圆心角相同时,趋于稳定,随跨径、半径变化不甚剧烈,圆心角φ 是Kqf的决定参数。
图7 反映了基于“准则二”的中墩采用双支座的三跨钢梁Kqf—R变化规律:(1)相同曲率半径时,桥梁抗倾覆稳定系数随跨径(或圆心角φ)增大而减少;(2)曲率半径R>200 m 时(即圆心角φ<21.5°~34°),Kqf趋于稳定,随跨径变化不甚剧烈,这与文献[4]关于“曲梁圆心角在φ<22.5°~30°时主梁受力可忽略扭转影响”的结论吻合。
由此可见,通过控制曲梁的长度从而减少圆心角φ,可以有效改善曲线桥梁抗倾覆稳定性能。实际设计中,圆心角φ、桥梁半径和桥梁长度是互为制约,在总体设计时需统一考虑。

图6 Kqf-φ 变化φ 曲线
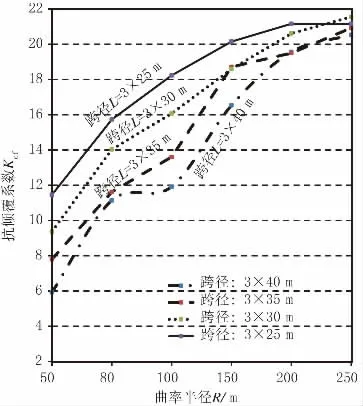
图7 Kqf - R 变化曲线
4 结 语
支座布置、平面圆心角φ 和曲率半径是影响桥梁抗倾覆稳定性的重要因素。中墩采用双支座能有效约束主梁扭转变形,从而提高桥梁抗倾覆能力;同时,通过控制一联桥梁的长度从而减小圆心角φ,也可以有效改善曲线钢桥的抗倾覆稳定性能。

