离子注入机分析器模型的自动调束控制方法

孙 勇，钟新华，杨亚兵

(1. 中国电子科技集团公司第四十八研究所， 湖南 长沙410205；2. 北京烁科中科信电子装备有限公司， 北京101111)

近几年随着我国集成电路制造的高速发展，用户对集成电路生产设备离子注入机的精度、重复性、稳定性、产能和自动化等要求也越来越高。为适应市场要求，本文提出了一种基于离子注入机分析器模型的自动引束控制方法。此方法是通过获得离子注入机分析器精确模型，减少自动引束的调整时间，大大提高了自动引束的效率和成功率，从而提高了离子注入机设备的生产效率和稳定性。

这种方法采用霍尔探头(Hall Probe)来测量质量分析器的实际磁场。为了保证测量的准确性，利用离子注入机光路理论模型对霍尔探头进行校准，实验验证了此测量方法的准确性和稳定性。采用在线辨识方法获取质量分析器的实际模型，用于控制器的前馈控制，提高了离子注机分析的调节控制效率和稳定性。

1 原理

离子注入机通过离子束加速器、质量分析器、平行透镜等光路部件将符合设定质量数、电荷数和能量的离子注入到晶片表面。其中质量分析是将同一能量的不同质量数的离子束经过一个特定的磁场、将符合质量数要求的离子分离出来。离子注入机的光路如图1 所示，对给定动能、质量数m和电荷数q的离子，其曲率半径r是特定的，是由磁场大小决定的。通过调整分析器的磁场大小，使之产生与机器光路几何形状相匹配的离子曲率半径，才能保证给定的动能、质量数和电荷数的离子通过光路狭缝。

根据洛伦兹力定律，离子在磁场中的运动轨迹计算公式为：

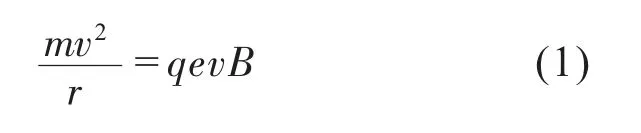
式(1)中，B为磁场强度，r为曲率半径，v为离子运动速度，m为离子质量，q为电荷数，e为电荷常数（1.6×10-19C）。

在不考虑热损耗的条件下，根据能量守恒定律可得：

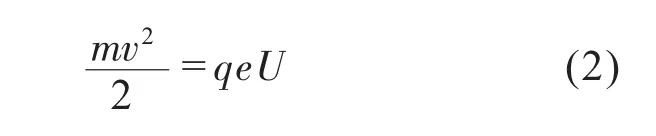
其中，U为加速电压，单位为V。

由式(1)、(2)得：

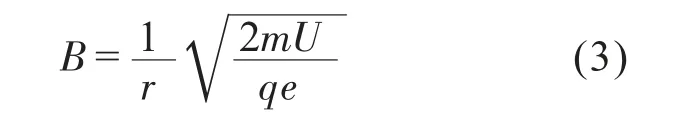
其中，E=qU，为注入能量，单位eV，m为离子的质量数。将磁刚度R代入公式3 可得：

由式(4) 可以得出磁场强度与离子的磁刚度是理想的一次线性关系。

图1 离子注入机光路示意图

2 磁场测量与校准

由于Hall Probe 输出电压受磁场强度B、安装位置和DC 电压漂移等因素影响，因此需要通过Analyzer 理论模型（公式4）对磁场测量系统进行校准，校准方法为：

式(5)中，B为磁场强度，VHP为Hall Probe 的电压，k为系数，c为截距。

系数k和截矩c通过几组不同的Beam 和最小二乘法求得。VHP对应的磁场强度可由公式B=求得，其中R为磁刚度，r为转变半径。

3 分析器模型校准

由于分析器的实际磁场模型与理论模型存在差别，为了能够实现精确控制，需要对分析器实际模型进行修正，采用二次模型进行修正，即：

式(6)为离子刚度R与Hall Probe 测量的磁场强度B 的关系式，用于分析器控制器的反馈控制。

为提升控制器的调节速度，减少自动调束(Auto Tune Beam)耗时，提高设备的生产效率，建立了分析器磁场B 和分析器线包电流I 的关系统模型：

由式(7) 可以提前预测磁场线包所需的控制电流，模型用于分析器控制器的前馈控制。

校准过程中要遵守磁刚度R 从小到大的原则，磁场电流从零增加到目标值的方向设置，这样尽可能避免磁铁的磁滞效应的影响[1]。

4 实验验证

首先对Hall Probe 校准模型公式(5)进行实验验证和参数获取，实验方法是在CIP900 型离子注入机上、通过不同能量、不同元素的离子束获取最优数据，并进行最小二乘拟合，图2 为Hall Probe校准模型的拟合结果，相关系数优于R2=0.9993。

图2 Hall Probe 校准模型拟合结果

以同样的实验方法对公式(6)和公式(7)进行多项式拟合，实验结果如图3 和图4 所示。

图3 磁场B 与磁刚度R 的拟合结果

图4 分析器电流与磁场的拟合结果

通过建立可靠的Hall Probe 校准方法，可以精确测量出分析器的真实磁场强度，以免被其它干扰。利用模型公式(6)和模型公式(7)，在束流能量、质量数和电荷量已知的情况下，就能快速预先计算出分析器电流，从而避免了通过找束流峰值的方法来确定正确的磁铁设置值，减少了分析器调节时间，提高了设备自动调束的效率和成功率。该方法在ZKX CIP 300 型离子注入机进行了测试，自动调束时间缩短了1 min 以上[2]。

5 结论

利用霍尔探头实时测量分析器的磁场并反馈给分析器控制器进行实时控制，这种方法应用到标准的中束流离子注入机进行了广泛的实验测试，结果表明，该方法与传统的找峰值自动调束方法相比，无论是调节效率，还是稳定性都有较大的提高。