X射线脉冲星TOA数量对计时精度和导航的影响分析

韩孟纳，童明雷，朱鸿旭，赵成仕，朱幸芝

X射线脉冲星TOA数量对计时精度和导航的影响分析

韩孟纳1,2,3，童明雷1,2，朱鸿旭4，赵成仕1,2，朱幸芝1,2

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 时间频率基准重点实验室，西安 710600；3. 中国科学院大学，北京 100049；4. 山东航天电子技术研究所，烟台 264000）

针对XPNAV-1卫星发布的Crab脉冲星首批数据，采用Taylor频域相关法得到了脉冲到达时间（TOA）及其对应的测量精度。在此基础上，去掉光子数量过少的第5组数据，得到34组数据的拟合前计时残差的均方根（RMS）约27.1 µs，拟合后计时残差RMS约22.5 µs。将光子数量最多的第24组观测数据按照不同的光子数量分组，得到了脉冲轮廓信噪比、TOA测量精度及计时残差与光子数量之间的关系。考虑空间飞行器实时定位需求，本文分析了在保障一定信噪比的前提下增加TOA数量对定位精度的影响。将观测数据按20000个光子重新分组，得到了214个TOA，其拟合前计时残差RMS约为61.8 µs，拟合后计时残差RMS约61.3 µs。这不但大大提高了导航的实时性，而且将定位精度提高了约10%。

X射线脉冲星；脉冲星计时；光子个数；脉冲轮廓

0 引言

现代卫星导航系统能够为地球表面和近地空间的各类用户提供全天候、高精度的自主导航信息服务，但是地球卫星导航却无法对执行深空探测和星际飞行任务的航天器导航。在深空探测与星际飞行任务中，航天器距离地球很远，相对于地球卫星来说，对深空航天器的位置确定以及姿态控制难度较大。考虑到在深空探测器跟踪、导航中，陆基系统由于频繁的地面操作以及导航误差随测控距离的增加而线性增大等问题，利用地面测控系统对在轨航天器进行轨道监测与位置修正是不方便的，航天器最好能够自主导航，而其中一种具有很大发展前景的航天器自主导航方法就是基于X射线脉冲星计时的导航方法[1]。X射线脉冲星导航的自主性强，信号源为宇宙中的自然天体—脉冲星，可以减少航天器对地面测控系统的依赖，将广泛应用于航天器深空探测和星际飞行任务[2-4]。

脉冲星为高速自转的致密天体，其磁极产生强磁场，磁场随星体的旋转产生感应电场，电子被加速离开星体表面，产生辐射光束，如同灯塔的光束[5]。当辐射束扫过地球，可被地面射电望远镜接收或空间X射线探测器探测。脉冲星的自转具有高度稳定性，尤其是毫秒脉冲星。脉冲星的多方面应用，如建立脉冲星时间尺度[6-8]、探测低频引力波[9]、计算太阳系行星质量[10]以及脉冲星导航[11-12]等，都是基于它自转的高度稳定性的[13]。目前发现的众多脉冲星中，有不少具有从射电到X射线的全波段辐射，这将使我们更清楚地认识脉冲星的辐射机制及其内部结构。脉冲星辐射的X射线光子易于被小型化探测器接收，这有利于减少航天器有效载荷的尺寸。脉冲星按照旋转能量来源可分为三类，分别为旋转供能脉冲星、吸积供能脉冲星和磁星。吸积供能脉冲星多位于双星系统，主要通过吸取伴星的物质来提供辐射所需的能量，自转极不稳定[14]。X射线脉冲星导航所选用的脉冲星须为旋转供能脉冲星，且同时具有X射线波段与射电波段的辐射。之所以要具有射电波段的辐射，是为了得到脉冲星星历并建立脉冲星计时模型。蟹状星云（Crab）脉冲星（B0531+21）正符合脉冲星筛选条件，可应用于X射线脉冲星导航。Crab脉冲星位于超新星1054 AD中心处，是恒星超新星爆发后在蟹状星云中的残骸，其自转周期约为33 ms，在X射线波段具有很强的流量。但由于Crab脉冲星比较年轻，为得到高精度的计时模型，其历表需要频繁更新。

脉冲星导航试验卫星（XPNAV-1）是我国首颗X射线脉冲星导航试验卫星，该卫星由中国航天科技集团第五研究院研制，并于2016年11月10日在酒泉卫星发射中心发射升空[15]。2017年5月9日，北斗卫星导航系统网站发布了35组首批由星载Wolter-I聚焦型探测器探测到的Crab脉冲星数据，探测器的各项性能参数如表1所示[16]。XPNAV-1卫星主要用于验证星载X射线探测器的性能和其对空间环境的适应力，并通过积累在轨观测数据完善脉冲星导航算法，为未来航天器深空导航奠定基础。本文主要采用XPNAV-1卫星的发布数据进行相应的处理与分析。

表1 Wolter-I聚焦型X射线探测器性能参数

1 观测数据处理流程与方法

1.1 TOA的获取

XPNAV-1卫星的发布数据给出了卫星的轨道与光子事件两个文件。其中，轨道文件包括轨道遥测历元与遥测时刻卫星的状态向量两部分，光子事件文件包括光子TOA（光子到达探测器的时刻）以及每个光子的能量。X射线探测器探测到Crab脉冲星辐射的X射线光子，并由星载原子时钟记录光子到达探测器的时刻。光子TOA采用UTC秒的记录形式，即光子被捕获时刻相对UTC 2008年1月1日0时0分0秒的秒数[16]。X射线光子到达卫星的时刻与卫星状态向量的遥测时刻并不一致，因此，需要在光子到达探测器的时刻内插出航天器的位置与速度，内插的方法采用一维线性插值。

卫星在观测过程中不断绕地运动，其所处的引力场在不断变化，星载时钟记录的光子到达时刻需转化到惯性系中的某一参考点。太阳系质心天球参考系（barycentric celestial reference system，BCRS）是一个准惯性系，可用于描述XPNAV-1卫星的轨道运动和脉冲星的观测信息（如角位置）。我们将Crab脉冲星光子到达探测器的时刻转换到BCRS的坐标原点——太阳系质心（solar system barycentre，SSB）。此过程主要涉及相应参考系与时间系统的转换[16]。X射线波段观测相对于射电观测的一个优点在于：X射线波段观测无需考虑信号在星际介质中的色散效应以及地球大气传播时延。由于发布的Crab脉冲星星历未考虑视差项，为自洽本文也不予考虑，只进行Roemer时延、Shapiro时延以及Einstein时延的改正。

Roemer时延项为航天器相对于SSB的距离在Crab脉冲星视线方向上的投影所产生的时间延迟量，也将其称为真空传播时延。Shapiro时延项是由于太阳系中的大质量天体引起时空弯曲，与平直时空相比这将引起额外的时间延迟[17-18]。由于地球公转轨道并非严格的圆轨道，且太阳的引力场效应不可忽略，在地球上实现的原子时从太阳系全局来看并不是均匀的，必须扣除太阳系引力场与地球相对太阳系质心运动速度的影响，将时间基准定义到太阳系质心参考系。脉冲星计时观测确定的脉冲星星历参数必须明确说明所参考的时间尺度。BCRS对应的时间尺度为太阳系质心坐标时（TCB），而由于历史原因，美国NASA喷气推进实验室（JPL）给出的、用于描述太阳系天体的位置与速度的行星历表采用的时间尺度是太阳系质心力学时（TDB），TDB与TCB之间不存在周期性差异，仅存在线性速率差。由于Crab脉冲星的星历归算采用的是TDB，因此须将光子到达时刻最终转换为TDB。Einstein时延项涉及协调世界时（coordinated universal time，UTC）到TDB的时间系统转换[19]。转换过程需考虑两个效应，即狭义相对论中的“时钟变慢”效应（运动的时钟会变慢）与广义相对论中的“引力红移”效应（所处的引力场越强，原子钟的走时速率越慢）。各种时间尺度转换公式如下[20-22]：

在计算光子到达SSB处的时刻时，需要使用太阳系历表给出太阳与大行星的质量以及观测时刻各天体到SSB的距离等，一般使用JPL发布的DE系列历表。由于Crab脉冲星星历[23]是使用DE200历表[24]得到的，为保持一致，本文做光子到达SSB的时刻转换时，太阳系历表依然选用DE200。至此，经过一系列的计算后，得到了光子到达SSB的时刻。利用光子到达SSB的时刻，在SSB处进行脉冲轮廓折叠，分别得到积分脉冲轮廓与标准脉冲轮廓，然后将二者做互相关处理得到TOA。积分脉冲轮廓是以起始观测时刻为起点折叠得到，至于利用多少光子数据能得到相对稳定的积分脉冲轮廓，将在下文讨论。标准脉冲轮廓需要更长积分时间的数据，为提高信噪比，这里采用全部的35组数据折叠形成。本文Crab脉冲星的标准脉冲轮廓是以英国Jodrell Bank天文台发布的Crab脉冲星星历定义的参考历元为起点折叠得到，星历定义的参考历元是射电观测得到的TOA。由于卫星观测数据为X射线波段观测得到，与脉冲星星历所采用的射电数据属于不同的波段，因此折叠出来的标准脉冲轮廓存在0.198 ms的零点相位差。标准脉冲轮廓如图3所示。因脉冲轮廓经离散傅里叶变换（DFT）之后在频域互相关[25-26]，与简单的进行时域互相关相比，其得到的相位偏移量更加精确，TOA测量精度更高，所以本文的TOA是采用积分脉冲轮廓与标准脉冲轮廓经DFT之后在频域互相关的方法得到的。最终，TOA通过起始观测时刻加上由相位偏移量转化的时间偏移量来确定。

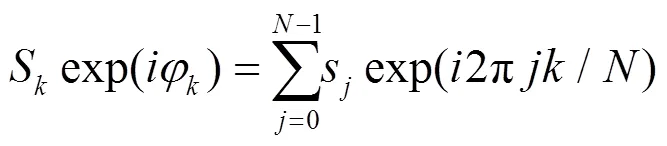
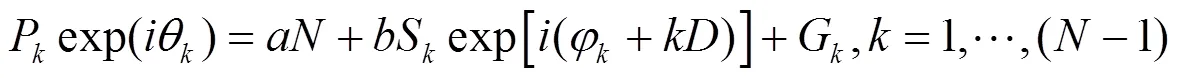
计时残差为测量的TOA与脉冲星计时模型在SSB处预报的TOA之差，即[5]：

式（15）中，A为探测器有效面积，T为总的观测时间，P为脉冲周期，s为脉冲星辐射流量，b为背景X射线光子到达速率，参数与分别表示X射线光子信号本身的固有噪声和背景噪声影响下脉冲形状对TOA测量精度的影响。由公式（16）可以看出，若探测器飞行环境近似一致，用相同的探测器观测同一颗脉冲星时，TOA不确定度与观测时间之间存在关系。观测时间越长，探测器积累的光子数越多，观测时间与光子数近似为线性关系。因此，TOA测量的不确定度与光子数之间近似满足平方反比关系。图2中曲线是TOA不确定度拟合曲线，拟合曲线方程为，其中=5 492.3。拟合方程中的、分别为光子数与。由图2可知，光子数越多，测量的TOA不确定度越小，平方反比关系成立。

图2 光子个数与TOA不确定度的关系

1.2 观测数据分组方案

航天器的初始轨道位置由轨道力学模型给出，航天器在轨运动时并不会严格按照预定轨道运行，真实位置与估计位置会有偏差，需要对偏差值进行实时修正。而确定航天器的位置估计误差主要是通过将测量的脉冲到达SSB时间与脉冲星计时模型在SSB处预报的TOA的差值来加以改正[12]。由于测量的TOA误差与积分脉冲轮廓的信噪比成反比，因此使用多长的观测数据可以得到相对稳定的脉冲轮廓是一个值得研究的问题。虽然较长的积分时间会形成高信噪比的脉冲轮廓以及较小的统计测量误差，但是如果积分时间过长，就会得到较少的积分脉冲轮廓，从而得到较少的TOA，降低了导航效率，无法对航天器的位置误差做出实时修正。

下面针对至少需要多少个光子可以形成相对稳定的积分脉冲轮廓这一问题来开展研究。由于第22组与24组观测数据的光子数最多，数据量分别为287 446与300 627，先使用这两组数据试验。将两组数据依次按照每组150 000、100 000、75 000、60 000、50 000、37 500、30 000、25 000、20 000、18 750、15 000、10 000个光子数分组。假设观测过程中探测器所处的空间环境近似相同，我们定义信噪比（SNR）：归一化的平滑标准脉冲轮廓与噪声的比值。这里的噪声是积分脉冲轮廓与平滑标准脉冲轮廓光子数经归一化后的对应值之差。将标准脉冲轮廓平滑处理是为了更加真实地还原脉冲信号。我们采用Savitzky-Golay平滑方法，这种方法通过平滑局部数据多项式回归来实现曲线的平滑，能够有效地保留数据的原始特征。在平滑过程中，平滑值不能设置的过大，否则会导致脉冲轮廓波形失真。平滑之后的标准脉冲轮廓如图3所示。脉冲轮廓归一化方法为每个bin对应的光子数减去其最小值（具有最少光子bin内的光子数）之后除以极差（最大值-最小值），这样得到的脉冲轮廓位于[0，1]之间。将第22组数据与第24组数据依次按不同光子数进行分组之后，得到每组光子个数与对应积分脉冲轮廓SNR均值的关系如图4所示。随着光子个数的增多，积分脉冲轮廓SNR均值有一定的起伏，但整体呈上升趋势。说明折叠所用的光子数越多，积分脉冲轮廓的信噪比越高，脉冲轮廓越稳定。

图3 未平滑与经过平滑之后的标准脉冲轮廓

图4 光子个数与SNR均值的关系

表2给出第24组数据分组之后每组光子个数与其对应的平均TOA不确定度的关系，而图5给出了更直观的展示。可以看出，在数据总量相等的情况下，随着每组光子个数的增加，TOA不确定度逐渐下降。由此可知光子个数越多，折叠出的脉冲轮廓越稳定，与图2得到的结论一致。此外，从图5可以看出，计时残差的RMS值随着光子个数的增加也有减小的趋势。

表2 第24组数据再次分组后的平均TOA不确定度

图5 不同光子数量对应的TOA不确定度及计时残差特征

图6展示了TOA不确定度的变化率随光子个数的增加不断变小，当光子数足够多时，TOA不确定度的变化率趋于零。说明随着积分时间的不断增加，脉冲轮廓稳定度最终将达到饱和。在分组折叠过程中，每组光子个数达到20 000个以上时，脉冲轮廓的波峰才能体现出来。因此，为形成高质量积分脉冲轮廓，光子个数最好能超过20 000个。

图6 光子个数与TOA不确定度变化率的关系

2 分组前后计时残差及测量精度比较与分析

在基于脉冲星计时的航天器自主导航中，利用星载X射线探测器接收脉冲星辐射的X射线光子，并将光子数据按前文介绍进行相应处理之后得到脉冲到达SSB的时间。如果航天器的位置不准，则将产生额外的计时残差。此时可以通过测量的脉冲到达时间（或相位）信息来给航天器定位，或者说对航天器做轨道修正以防偏离预设轨道太大。XPNAV-1卫星发布的数据每分钟可以获得800多个Crab脉冲星X射线光子数据。在获得积分脉冲轮廓时，若增加所需的光子数据量，则积分时间就要增加，同时数据处理过程耗时也会增加。若航天器处于磁场与引力场较强的极端飞行环境，在观测时间以及数据处理时间内，航天器的实际飞行轨道会严重偏离预定轨道。由于航天器的位置估计误差会随时间累积，若采用较长积分时间的观测数据作为一次有效观测，反而增加位置修正的时间与难度，航天器的轨道无法实时修正。因此，在积分脉冲轮廓折叠时，光子数据量的选取需要权衡观测积分时间与脉冲轮廓信噪比，在保证脉冲轮廓信噪比的同时，减少观测积分时间。在分析过程中发现，利用20 000个光子数据作为一次有效观测是合适的。

表3 分组前后计时残差及不确定度的比较

图7 XPNAV-1卫星214组观测数据的拟合前、后计时残差

3 结语

本文利用XPNAV-1卫星发布的Crab脉冲星X射线观测数据，以及英国Jodrell Bank天文台发布的Crab脉冲星的射电星历，分析了计时结果。首先得到了35组数据对应的TOA和拟合前计时残差。将光子数过少的第5组数据剔除后，得到34组数据拟合前计时残差的RMS值为27.117 6ms，拟合后计时残差的RMS值为22.525 6ms。将数据量最多的第22、24组数据按光子个数分组，并对分组数据处理，得到了光子个数与积分脉冲轮廓SNR及TOA不确定度的关系，验证了TOA测量精度随着光子个数的增加不断提高的结论。通过分析脉冲轮廓波峰的有无与波形的失真情况，发现20 000个光子可以形成相对稳定的积分脉冲轮廓。将去掉第5组后的34组数据按每组20 000个光子重新分组，得到了214个TOA，求得拟合前计时残差的RMS值为61.836 7µs，拟合后计时残差的RMS值为61.314 1 µs。与分组之前的结果相比，虽然拟合后的计时残差变大，但在损失一定脉冲轮廓信噪比的情况下获得了更多的TOA数据。若将此结果应用于脉冲星导航，则定位精度会提升约10%。

在应用X射线脉冲星的深空探测飞行器导航中，采用较长积分时间，可以提高TOA测量精度。但适当减少TOA观测积分时间，可以增加TOA观测数量，以便实时性地修正飞行器轨道误差。合理斟酌TOA的测量精度与观测数量是非常必要的。本文脉冲到达时间是通过将脉冲轮廓折叠后形成的积分脉冲轮廓与标准脉冲轮廓进行互相关得到的，在脉冲轮廓折叠过程中会损失单个光子相位信息。而利用最大似然估计法可以在航天器处直接获得TOA且无需进行脉冲轮廓折叠[29-30]。后续的工作中，可以考虑用这种方法来确定TOA，提高导航的实时性。

[1] 杨廷高. X射线脉冲星脉冲到达航天器时间测量[J]. 空间科学学报, 2008, 4(4): 60-64.

[2] 郑伟, 王奕迪, 汤国建, 等. X射线脉冲星导航理论与应用[M]. 北京: 科学出版社, 2015.

[3] SHEMAR S, FRASER G, HEIL L, et al. Towards practical autonomous deep-space navigation using X-Ray pulsar timing[J]. Experimental Astronomy, 2016, 42(2): 101-138.

[4] RAD A, AZARI L. Determining attitude and position in deep space missions using X ray pulsars[J]. International Journal of Astronomy and Astrophysics, 2014, 4(4): 628-648.

[5] LORIMER D R, KRAMER M. Handbook of Pulsar Astronomy[M]. Cambridge: Cambridge University Press, 2005.

[6] HOBBS G, COLES W, MANCHESTER R N, et al. Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society, 2012(427): 2780-2787.

[7] PETIT G, TAVELLA P. Pulsars and time scales[J]. Astronomy and Astrophysics, 1996, 308(1): 290-298.

[8] 童明雷, 杨廷高, 赵成仕, 等. 脉冲星计时模型参数的测量精度分析与估计[J]. 中国科学(物理学 力学 天文学), 2017, 47(9): 9503.

[9] HOBBS G, ARCHIBALD A, ARZOUMANIAN Z, et al. The international pulsar timing array project: using pulsars as a gravitational wave detector[J]. Classical and Quantum Gravity, 2010, 27(8): 4013.

[10] CHAMPION D J, HOBBS G B, MANCHESTER R N, et al. Measuring the mass of solar system planets using pulsar timing[J]. The Astrophysical Journal Letters, 2010, 720(2): 201-205.

[11] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation[D]. Maryland: University of Maryland, 2005.

[12] BECKER W, BERNHARDT M G, JESSNER A. Autonomous spacecraft navigation with pulsars[J]. Acta Futura, 2013(7): 11-28.

[13] TAYLOR J H. Millisecond pulsars: nature's most stable clocks[J]. Proceedings of the IEEE, 2002, 79(7): 1054-1062.

[14] GALLOWAY D, BASSA C, WANG Z, et al. Accreting neutron star spins and the equation of state[J]. AIP ConferenceProceedings, 2008(983): 510-518.

[15] GUO Qian. LM-11 successfully Launched XPNAV-1[J]. Aerospace China, 2016, 17(4): 61-61.

[16] 北斗网. 脉冲星试验01星在轨试验数据[EB/OL]. (2017-05-09) [2020-06-01]. http://www.beidou.gov.cn/yw/xwzx/201710/t20171010_824.html.

[17] EDWARDS R T, HOBBS G B, MANCHESTER R N. TEMPO2, a new pulsar timing package-II. The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(4): 1549-1574.

[18] SHAPIRO I I. Fourth test of general relativity[J]. Physical Review Letters, 1964, 13(26): 789-791.

[19] PETIT G. From atomic clocks to coordinate times[J]. Proceedings of the International Astronomical Union, 2007, 2(14):478-478.

[20] International Astronomical Union. IAU 2006 Resolution B3[EB/OL]. (2020-03-12) [2020-06-01]. http://www.iau.org/static/resolutions/IAU2006 Resol3.pdf.

[21] International Astronomical Union. IAU 2000 Resolution B1[EB/OL]. (2020-03-12) [2020-06-01]. https://www.iau.org/static/resolutions/IAU2000_French.pdf.

[22] FUKUSHIMA T. Time ephemeris and general relativistic scale factor[J]. Proceedings of the International Astronomical Union, 2009, 5(261): 89-94.

[23] LYNE A G, PRITCHARD R S, GRAHAM-SMITH F. Jodrell Bank Crab Pulsar Monthly Ephemeris[EB/OL]. (2020-03-21) [2020-06-01]. http://www.jb.man.ac.uk/pulsar/crab.html.

[24] Jet Propulsion Laboratory. Planetary Ephemeris DE200[EB/OL]. (2020-02-15) [2020-06-01]. https://naif.jpl.nasa.gov/pub/naif/generic_kernels/.

[25] 杨廷高, 童明雷, 赵成仕, 等. Crab脉冲星X射线计时观测数据处理与分析[J]. 天文学报, 2018, 59(2): 10-16.

[26] TAYLOR J H. Pulsar timing and relativistic gravity[J]. Philosophical Transactions: Physical Sciences and Engineering, 1992, 341(1660): 117-134.

[27] 朱鸿旭, 童明雷, 杨廷高, 等. XPNAV-1卫星先期发布数据的计时分析[J]. 宇航学报, 2019, 40(12): 1492-1500.

[28] 帅平, 李明, 陈绍龙, 等. X射线脉冲星导航系统原理与方法[M]. 北京: 中国宇航出版社, 2009: 431-434.

[29] RAY P S, KERR M, PARENT D, et al. Precise gamma-ray timing and radio observations of 17 fermi gamma-ray pulsars[J]. Astrophysical Journal Supplement, 2011, 194(2): 17.

[30] LIVINGSTONE M A, SCOTT S M, CAMILO F, et al. X-ray and radio timing of the pulsar in 3C 58[J]. Astrophysical Journal, 2009, 706(2): 1163-1173.

Analysis of the influences of TOA number on timing precision and navigation

HAN Meng-na1,2,3, TONG Ming-lei1,2, ZHU Hong-xu4,ZHAO Cheng-shi1,2, ZHU Xing-zhi1,2

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China；2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China；3. University of Chinese Academy of Sciences, Beijing 100049, China；4. Shandong Institute of Space Electronic Technology, Yantai 264000, China)

Using the first public data set of Crab pulsar observed by XPNAV-1 satellite, we obtained the resulting pulse times of arrival (TOA) and the uncertainty using the Taylor frequency domain correlation method. After removing the fifth group of data for its too few photons, we obtained the root-mean-square (RMS) of the pre-fit and post-fit timing residuals of the 34 groups left to be about 27.1 µs and 22.5 µs, respectively. The data in the 24th group, which is with the most photons, were divided according to various photon quantities. The relations between the signal to noise ratio (SNR) of the pulse profiles, and the measurement uncertainties of TOA and the timing residuals, and the number of photons were obtained. On the real-time positioning requirements from spacecrafts, the effect of increasing the number of TOAs while maintaining a given SNR on the positioning precision is analyzed. By regrouping the whole data set by 20 000 photons, 214 TOAs were obtained, and the RMS of the pre-fit and post-fit residuals are about 61.8 µs and 61.3 µs. It not only largely enhances the real-time of the navigation, but also improves the positioning precision by about 10 percent.

X-ray pulsar; pulsar timing; number of photons; pulse profile

10.13875/j.issn.1674-0637.2021-01-0066-11

韩孟纳, 童明雷, 朱鸿旭, 等. X射线脉冲星TOA数量对计时精度和导航的影响分析[J]. 时间频率学报, 2021, 44(1): 66-76.

2020-06-12；

2020-07-20

国家自然科学基金资助项目（U1831130；U1531112；11873050）；中国科学院青年创新促进会资助项目（2017450）