一种基于稀疏信号的时差频差联合估计方法研究
王善和,华宇,高媛媛,向渝,黄长江,赵弦,薛伟成
一种基于稀疏信号的时差频差联合估计方法研究
王善和1,2,华宇1,高媛媛1,向渝1,黄长江1,赵弦1,薛伟成2
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院大学,北京 100049)
基于非合作信号的时差频差估计是无源探测中的关键技术之一。对于给定信号,为提高时差估计精度,可通过提高采样率或增加采样时长来实现,但是增加了数据存储和传输的成本。因此,针对在频域上稀疏的信号,结合相关函数的性质,本文通过理论分析与推导,给出了一种时差频差联合估计方法。数据仿真结果表明该方法与传统的互模糊函数法相比,在相同的时差频差估计精度下,能显著地压缩原始数据的存储容量,减少数据存储和传输的压力。
时差频差联合估计;稀疏信号;无源探测
0 引言
无源定位已经成为电子对抗最重要的技术之一,该技术自身不发射信号,不容易受到干扰和攻击,因此具有较好的隐蔽性和战场生存力[1]。无源定位中常用的测量基础是辐射源方位测量和时差测量,而对于目标辐射的非合作信号到达两个接收站的时差可以采用互相关函数进行估计,如广义互相关法[2-3]、自适应滤波算法[4]、互功率谱相位算法[5]、小波变换法[6]等。若要提高探测精度,上述方法都需要大量的观测数据以提高相关增益,给数据保存和传输方面带来了压力。
为突破采样数据不断增加的瓶颈,国外一些学者开展了基于压缩感知(compressed sensing)[7-8]的时差估计,如2010年K. Gedalyahu采用压缩感知思想提出低采样率的时延估计方法[9],2013年K. Fyhn提出的用内点法进行压缩感知时延估计[10],2017年Yujie Gu提出的压缩感知核优化方法时延估计及克拉美罗边界估计方法[11],这些理论与方法都是根据信号在某种变化下具有稀疏性的特点,对被采样信号以远低于奈奎斯特采样定理的要求对信号进行压缩采样,且可保证一定的时差估计精度,但这些方法都是针对体制已知的信号在研究,尤其是雷达发射的脉冲信号。
本文融合压缩感知技术在无源探测方面的应用,开展对信号体制未知的卫星辐射信号进行研究,提出基于稀疏信号的时差频差联合估计方法(简称为稀疏估计法),通过将观测数据进行稀疏化处理,一方面能够解决混频和采样时频率与相位不一致导致的时差频差估计精度低的问题,另一方面可以去除部分噪声,提高时差频差估计精度,同时也便于下一步的数据压缩与传输,减少无源授时与定位系统对数据链的要求[12]。
1 时差频差联合估计方法
1.1 稀疏信号
稀疏信号是指信号中非零元素非常少,大多数元素为零,或者近似为零。通常情况下的信号并不是稀疏信号,但是经过某种变换后可能成为稀疏信号,比如简单的正弦波组合采样信号

卫星辐射信号为人造信号,经傅里叶变换或小波变换后,大部分信号都具有稀疏性,因此本文开展基于稀疏信号的时差频差联合估计方法研究。在给出该方法之前,先简要介绍一种常用的时差频差联合估计方法:互模糊函数法。
1.2 互模糊函数法


在信号接收过程中,一般先经过混频与滤波处理,将信号频率从射频变频为中频信号,比如为 70 MHz,再进行采样。由于两接收站本振信号的频率和相位存在一定的差异,一方面导致在下变频处理过程中引入频率和相位的偏差,影响时差估计精度;另一方面,本振信号的不同将导致采样率的不同,使得两接收信号的频谱不一致,进一步影响时差估计精度。
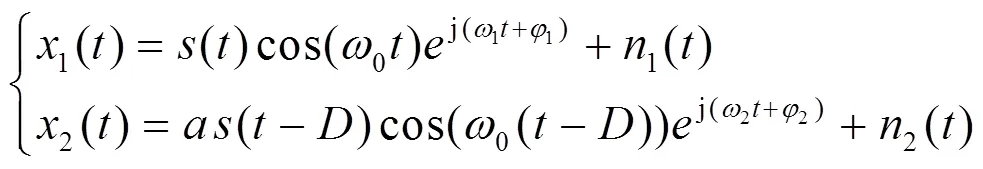
滤除高频项,得到
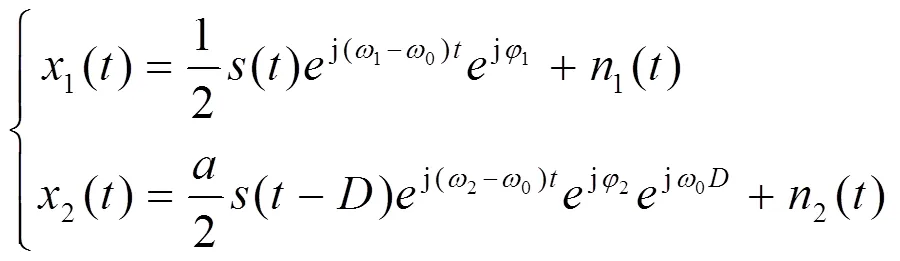

将式(5)代入式(6)得

利用柯西—施瓦茨(Cauchy Schwarz)不等式[13]有


1.3 基于稀疏信号的时差频差联合估计方法
式(5)经傅里叶变换,得



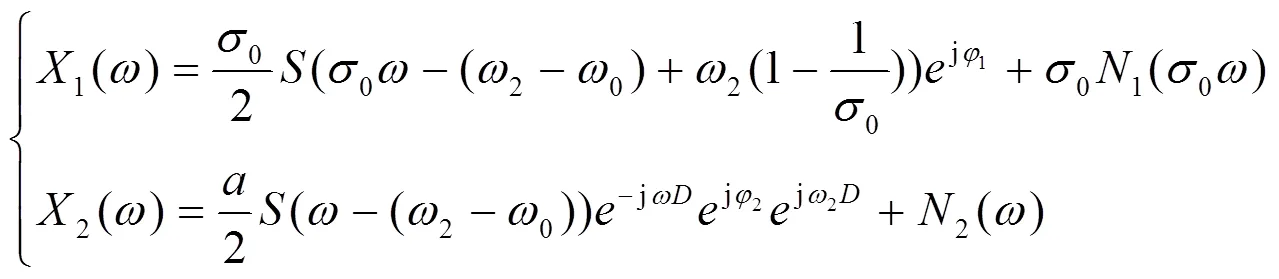

假设噪声为互不相关的零均值白噪声,信号与噪声相互独立,根据相关函数的性质,两个信号的相关函数和它们傅里叶变换的乘积互为傅里叶变换,结合式(9)有


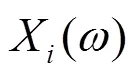
1.4 时差频差联合估计流程
基于稀疏信号的时差频差联合估计流程如图1所示。

图1 基于稀疏信号的时差频差联合估计流程图
结合图1,基于稀疏信号的时差频差联合估计的流程为:
① 1#站和2#站同时接收同一RF信号,与本地时钟的频率信号混频,下变频至IF信号;
② 两站通过本地时钟产生的采样频率对IF信号进行采样,得到离散信号;
③ 对离散信号进行FFT变换,仅保留大的分量,对信号进行稀疏化,并传输至同一地点;
2 仿真试验
为了验证基于稀疏信号的时差频差联合估计方法的有效性和时差频差估计精度,本节开展在高斯信道上对通信卫星信号与北斗卫星导航系统中B1I信号的时差频差联合估计方法的仿真验证,通过与互模糊函数进行比较,横向对比本文所提方法的时差频差估计精度。在以下仿真试验中均假设噪声为互不相关的零均值白噪声,信号与噪声相互独立。
2.1 通信卫星信号为辐射信号仿真试验

仿真过程中,对于图1中信号稀疏化过程本文采用对信号进行傅里叶变换后,仅保留大的幅值分量,较小的幅值赋值为零的方式。假定稀疏度设为99%,即稀疏化后幅值不为零的分量个数仅占原信号长度的1%,99%的分量均为零,图2给出了仿真信号的频谱图和稀疏化后的信号频谱图。


图3 通信卫星信号时差频差联合估计结果

表1 稀疏估计法对通信信号时差频差估计精度
从表1可以看出,随着稀疏度的提高,时差和频差的估计误差有增加的趋势,这是因为稀疏化程度越高,信号中所包含的信息量越少,导致相关峰的精度越低,但当稀疏度提高至99.99%时,信号中的有效信息太少,无法对时差和频差进行有效估计。另外,在稀疏度为90%时,时差的估计精度最高,这是由于稀疏化过程中保留了大量有效的信息,同时也滤除了部分噪声对时差估计的影响。
为了检验稀疏估计法在不同信噪比下的时差和频差估计精度,我们将一个信号的信噪比固定为 10dB,改变另一个信号的信噪比,在稀疏度设为50%和90%的情况下进行时差和频差估计。由于在较低信噪比下,时差或频差的估计误差可能会非常大,因此,本文将时差和频差估计偏差同时落在[-10 ns,10 ns]和[-10 Hz,10 Hz]区间上的比例作为方法性能优劣的判断标准,表2给出了稀疏估计法与互模糊函数法经过100次蒙特卡洛仿真试验对时差和频差的估计结果。其中,表2中等效信噪比定义为:
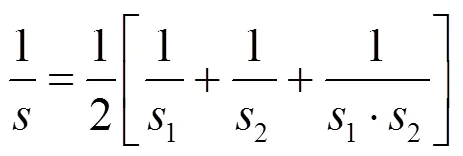
表2 不同信噪比下两种方法对通信信号的时差和频差有效估计率

表2表明随着信噪比的降低,两种方法对时差和频差的有效估计率都在下降。当等效信噪比大于-23.4 dB时,两种方法均可100%地有效估计出时差和频差;当等效信噪比小于-37.4 dB时,两种方法均无法有效估计出时差和频差。在稀疏率为50%的情况下,即保持原信号频谱几乎不变,稀疏相关法和互模糊函数对时差和频差的有效估计率基本相同;当稀疏率提高至90%的情况下,稀疏相关法对时差和频差的有效估计率有所下降。
2.2 北斗卫星导航B1I信号为辐射信号仿真试验

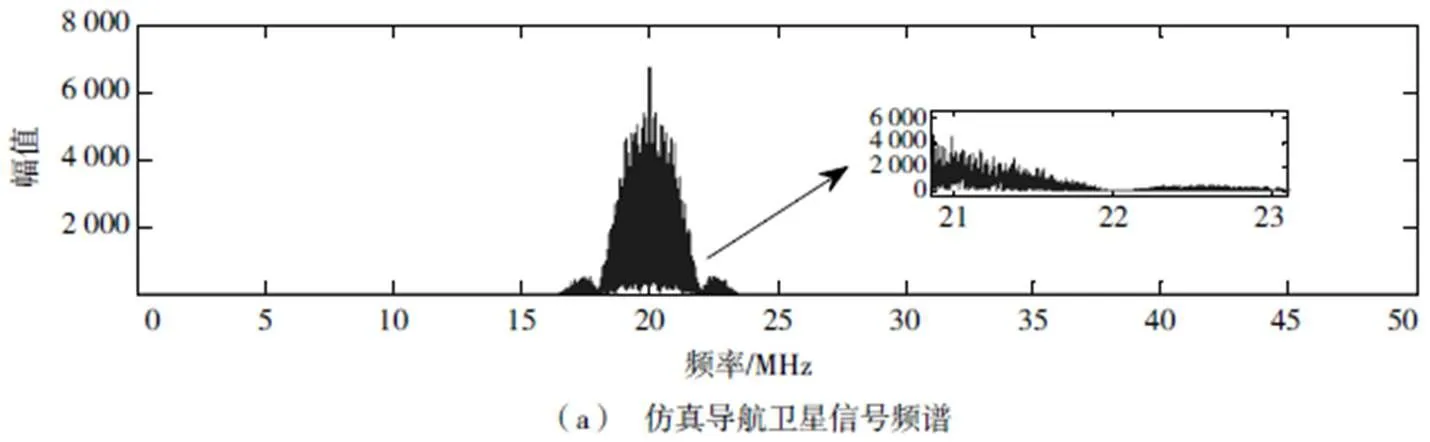
从图4可以看出,原始信号的频谱具有较好的稀疏性,稀疏度约为84%,但经过稀疏化过程后,稀疏度提高至99%。同通信卫星信号为辐射信号仿真试验的方法和参数保持一致,表3给出了稀疏估计法对时差和频差估计的RMSE统计结果,表4给出了在稀疏度设为90%和99%的情况下两种方法进行时差和频差估计的有效性统计结果。
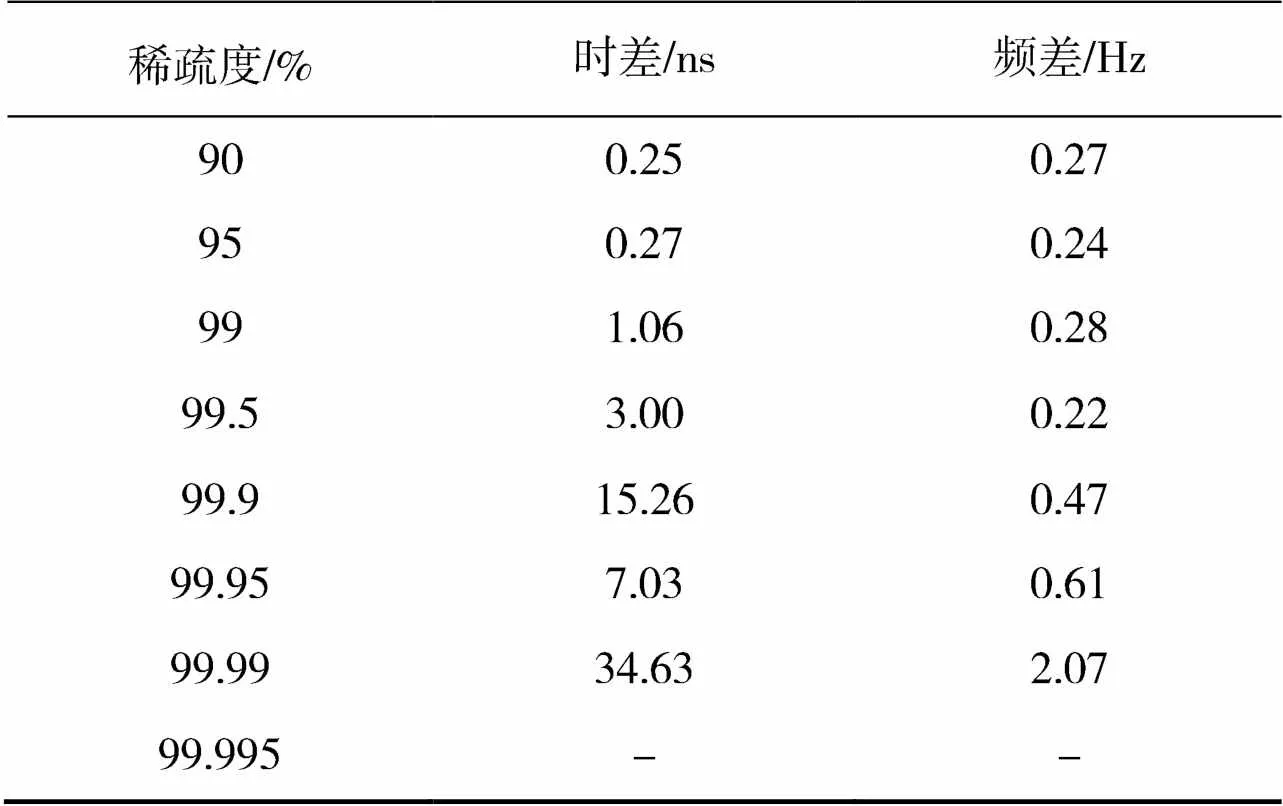
表3 稀疏估计法对导航信号时差频差估计精度
表4 不同信噪比下两种方法对导航信号的时差和频差有效估计率

从表3和表4的数据可以得出跟表1和表2类似的结论,不同之处在于导航信号的频谱本身稀疏度高,因此在更高的稀疏化过程后,如稀疏度设为99%,仍能够较好地估计时差和频差;同时,导航信号的带宽较窄,为了能够达到指定的估计精度,需要信号具有较高的信噪比。
2.3 仿真试验小结
综合比较上述仿真试验,可以得到如下结论。
① 使用信号的频谱数据或对频谱数据稀疏化程度不高时,利用稀疏估计法对时差和频差的估计精度与互模糊函数法相当。
② 对频谱数据稀疏化后仍可以对时差和频差进行有效估计,但稀疏度越高,对时差和频差的估计精度越低。
③ 在相同的时差和频差有效估计率的情况下,等效信噪比越高,可接受的稀疏度越高。
3 结语
基于稀疏信号的时差频差联合估计方法是通过对信号的频谱数据进行稀疏化和变换来实现时差和频差估计,在较高信噪比下,对于通信卫星信号和导航卫星信号可实现在高度稀疏化条件下的有效估计。在实际应用中,若两接收站利用1.2 m抛物面天线接收卫星下行信号,此时接收C波段卫星信号的信噪比约为0.4~16dB,可将稀疏率设为99%,压缩方法为记录非零系数的值和位置,尽管压缩后的数据仅有原数据的2%,但仍可以对时差和频差进行有效估计,这对于提高和优化无源探测系统具有重要的学术和应用价值。
[1] 胡来招. 无源定位[M]. 北京: 国防工业出版社, 2005: 1-3.
[2] KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976, 24(4): 320-327.
[3] CARTER G C. Coherence and time delay estimation[J]. IEEE Xplore, 1987, 75(2): 236-255.
[4] SO H C, CHING P C, CHAN Y T. A new algorithm for explicit adaptation of time delay[J]. IEEE Transactions on Signal Processing, 1994, 42(7): 1816-1820.
[5] NIKIAS C L, PAN R. Time delay estimation in unknown gaussian spatially correlated noise[C]//International Conference on Acoustics, Speech and Signal Processing, New York: [s.n.], 1988(5): 2638-2641.
[6] 王成刚. 基于小波变换和形态学的图像去噪方法研究[D]. 西安: 长安大学, 2009: 37-59.
[7] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[8] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[9] GEDALYAHU K, ELDAR Y C. Time-delay estimation from low-rate samples: a union of subspaces approach[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3017-3031.
[10] FYHN K, JENSEN S H, DUARTE M F. Compressive time delay estimation using interpolation[J]. Global Conference on Signal & Information Processing, 2013: 248-251.
[11] GU Y J, GOODMAN N A. Information-theoretic compressive sensing kernel optimization and bayesian Cramér-Rao bound for time delay estimation[J]. IEEE Transactions on Signal Processing, 2017, 65(17): 4525-4537.
[12] 高媛媛. 基于非合作卫星信号时差测量的无源定位方法与关键技术研究[D]. 北京: 中国科学院大学, 2018: 144-145.
[13] 孙晓莉. 柯西—施瓦茨不等式的推广与应用[D]. 合肥: 合肥工业大学, 2013.
[14] 吴丹. 通信信号调制方式分类识别算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2007: 12-13.
A joint estimation method of time difference and frequency difference based on sparse signal
WANG Shan-he1,2, HUA Yu1, GAO Yuan-yuan1, XIANG Yu1,HUANG Chang-jiang1, ZHAO Xian1, XUE Wei-cheng2
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. University of Chinese Academy of Sciences, Beijing 100049, China)
Joint estimation of time difference and frequency difference based on non-cooperative signals is one of the key technologies for passive detection. For a given signal, in order to improve the accuracy of time difference estimation, it can be achieved by improving the sampling rate or increasing the sampling time, but it will increases the cost of data storage and transmission. Therefore, for the signal sparse in the frequency domain, combined with the properties of the correlation function, this study proposed a joint estimation method of time difference and frequency difference through the theoretical analysis and derivation. Data simulation results shown that compared with the traditional corss-ambiguity function under the same accuracy of time difference and frequency difference estimation, this method can compress the storage capacity of original data significantly, thus reduces the pressure of data storage and transmission.
joint estimation of time difference and frequency difference; sparse signal; passive detection
10.13875/j.issn.1674-0637.2021-01-0001-09
王善和, 华宇, 高媛媛, 等. 一种基于稀疏信号的时差频差联合估计方法研究[J]. 时间频率学报, 2021, 44(1): 1-9.
2020-06-18;
2020-07-19
中国科学院国家授时中心“青年创新人才”资助项目(国授发字〔2017〕48号)

