森林生态系统涡度相关法碳通量长时间连续性缺失数据插补方法的比较*

周 宇，黄 辉，张劲松**，孟 平，孙守家

（1.中国林业科学研究院林业研究所，北京 100091；2.国家林业和草原局林木培育重点实验室，北京 100091；3.南京林业大学南方现代林业协同创新中心，南京 210037）

涡度相关法是目前测定大气与植被群落间净CO2交换（NEE）最直接、理论与技术发展最为迅速的一种微气象学方法，得到微气象学和生态学界的广泛接受和认可，广泛应用于全球不同陆地生态系统的物质与能量交换研究中，其观测数据也经常应用于各种模型的检验和验证[1]。由于涡度相关观测仪器需要定期进行校准和维护，观测过程中经常遇到难以避免的系统故障（仪器故障或供电系统故障等）和外界干扰（暴雨、连续阴雨、雾霾等恶劣天气条件等），涡度相关观测系统的原始数据往往会出现缺失；而在对通量数据进行数据质量控制后，如进行异常值剔除、低湍流条件（如夜间大气层结稳定等）下数据的剔除等，观测数据又会出现新的缺失。最终，年通量观测数据往往存在20%～65%的缺失，其中还可能出现较长时段的连续缺失（长达半个月，甚至一个月）[2−4]。为了获取完整和可靠的通量数据，需要采取合理的插补方法对缺失数据进行插补[5]。

目前，常用的数据插补方法主要有平均昼夜变化法（Mean Diurnal Variation，MDV）、查表法（Look-Up Table，LUT）、非线性回归法（Non-Linear Regression，NLR）、边际分布采样法（Marginal Distribution Sampling，MDS）和人工神经网络法（Artificial Neural Network，ANN）等[3,6−15]。选择不同的插补方法会产生不同的结果[1]。MDV 方法不依赖通量和环境变量的函数关系，插补夜间数据适合7d 的窗口，而日间适合14d 的窗口，在极端晴天或阴天条件下容易产生估算偏差[6]。LUT 方法通过气象变量建立索引表估计NEE，日间最适合使用气温，夜间适合使用土壤温度，而NLR 方法则利用生态系统呼吸方程和光响应曲线估算NEE。LUT 和NLR 方法的各个环境变量的分组越详细，插补效果越好，但均受到建立索引表或回归方程时所选取的时间阶段、站点光响应曲线的离散性、云量和干旱等因素的影响[6]。MDS 方法综合了MDV 与LUT方法，自动延长插补窗口，不需假设环境响应方程和预设初始值，被欧洲通量网和FLUXNET（全球长期通量观测网络）用作标准化处理[10]。ANN 方法在处理不同数量级和非连续变量方面具有巨大的优势，可通过更多的变量对NEE 进行插补，但在某些情况下输出结果可能不稳定[7]。是否进行u*校正对计算结果影响很大，u*校正通常使年总NEE更偏正[6]。保留NEE 与气象变量间基本生态学响应关系的方法能够取得较为认同的插补结果。综上，以往针对通量数据缺失插补方法的研究，大多关注不同插值方法在较短时间缺失情景下的插补性能，对不同方法在长时段且连续缺失情景下的插补精度和稳定性及其能够取得较好插补效果的缺失范围关注较少，且一直未形成通用的缺失数据插补方案。

本研究以华北低丘山地栓皮栎人工混交林生态系统为例，以基于涡度相关法观测得到的NEE数据为研究对象，在随机生成连续1、3、7、15和31d 数据缺失的情景下，选取平均昼夜变化法（MDV）、查表法（LUT）、非线性回归法（NLR）、边际分布采样法（MDS）和人工神经网络法（ANN）分别对50 个缺失数据集进行NEE 数据插补，探究不同插值方法在不同缺失情景下的插补精度和稳定性，并评估不同插值方法对缺失片段长度的敏感性，探讨不同插补方法所适用的连续数据缺失时长，以期为山地森林生态系统涡度相关法通量观测数据插补方法的选择提供参考，为准确估算区域碳收支、预测气候变化对碳储存及碳汇的影响、深入量化净生态系统碳交换等提供理论基础。

1 数据与方法

1.1 基准数据集

通量观测地点位于黄河小浪底森林生态系统国家野外定位观测研究站南山观测区（35°01'45''N，112°28'08''E，海拔410m）。该站位于河南省济源市辖区，地处太行山南麓与黄河中游的交错带。观测对象为栓皮栎（Quercus vari abilisBl.）、侧柏[Platycladus orie ntalis(L.) Franco]和刺槐（Robinia pseudoacacia）人工混交林生态系统，造林时间分别为1972年、1974年和1976年，平均株高分别为10.5、8.2 和9.3m，主要树种为栓皮栎（约占80%）。研究区属暖温带亚湿润季风气候，年平均气温为12.4℃。历年平均降水量为641.7mm，受季风气候影响，降水季节分配不均匀，5−9月平均降水量为438.0mm，占全年的68.3%[16]。生长季风向以东北偏东、西南方向为主。

涡度相关通量观测系统由CSAT3 型三维超声风速仪（USA）、LI-7500A 型开路式CO2/H2O 气体分析仪（USA）组成，安装高度距地面36m。数据采集器为SmartFlux 型（USA），原始数据采样频率为10Hz[17]。

小气候梯度观测系统包括7 层HMP155 型温湿度传感器（安装高度分别为5、8、11、14、18、26 和32m），6 层WindSonic 型二维超声风速计（安装高度分别为5、8、11、14、18 和26m），CNR1 型四分量辐射计（安装高度为17m），3 层土壤温湿度传感器（安装深度分别为 5、10 和20cm），土壤热通量计2 个（分别位于塔的东西两侧）[18]。数据采集器为CR1000 型，数据存储间隔为10min。

选取2017年3月1日−11月30日10Hz 通量观测数据，经涡度协方差数据分析软件EddyPro（USA）处理后，剔除数据质量标记为不可用的数据[19−20]，使用R Package ‘REddyProc’（https://github.com/ bgctw/REddyProc）计算摩擦风速阈值[10,21−22]，剔除低湍流条件（摩擦风速小于0.22m·s−1）下的观测数据[23]，将最终获得的 0.5h 尺度净生态系统碳交换量（NEE）数据作为基准数据集。NEE 基准数据集共有13200 条数据，数据缺失率为39%，其中白天（Rg＞20W·m−2）数据缺失率为32%，夜间（Rg≤20W·m−2）数据缺失率为48%。将小气候观测系统10min 气象数据聚合为30min，数据缺失率为9%，小于2h 的缺失数据用线性内插法插补，大于2h 的缺失数据采用平均昼夜变化法（MDV）进行插补，选择18m 位置处气温（Ta）、饱和水汽压差（VPD）、17m 处总辐射（Rg）作为气象基准数据集，用于数据插补。

1.2 数据缺失情景

为评估不同插值方法对缺失片段长度的敏感性，随机生成缺失片段重复次数不同，但缺失总数大致相同，以连续1、3、7、15 和31d 数据为缺失片段的5 类数据缺失情景（表1），各缺失片段分布均服从随机分布，每类缺失约占基准数据集的10%。为提高数据利用率，保证计算结果的准确性和稳定性，各类情景随机重复10 次，并与基准数据集相叠加，生成50 个缺失数据集。

表1 五类数据缺失情景Table 1 Description of five gap scenarios

1.3 数据插补方法

1.3.1 平均昼夜变化法

平均昼夜变化法（MDV）使用邻近一段时间内相同时段的观测平均值来代替缺失值，分为独立窗口法和滑动窗口法[6]。独立窗口法使用特定窗口内任一时间点在该时刻所有有效观测数据的平均值来代替缺失值（一般要求窗口内至少有4 个有效观测数据），滑动窗口法则使用缺失数据周围指定大小窗口内的所有有效观测数据的平均值来代替缺失值。窗口大小通常为4～15d。采用独立窗口法，即

式中，h（1，…，48）为一天中每0.5h 的索引，i[1，…，interger（d/n）+1]为平均窗口的索引，n 为窗口大小，d 为一年的天数，k 为一中间变量，上划线表示排除缺失数据后对该上滑线下的子集进行算术平均，下划线表示消除子集中缺失值后的索引。窗口大小选择：（1）固定窗口大小为15d，在连续缺失长达31d 情景下扩大为30d；（2）可变窗口，先以7d 为窗口插补数据，若还有数据缺失，则逐步扩大窗口为14d、21d、28d…，直至完成全部缺失数据插补。分别使用 Excel 和 R Package ‘REddyProc’sEddyProc_sFillMDC 命令基于窗口（1）和（2）进行缺失NEE 数据插补，分别记为MDV 和MDC。

1.3.2 查表法

查表法（LUT）基于6 个双月或4 个季节时段，建立特定站点各种气象条件下的NEE 索引表，根据缺失数据时段的气象条件在NEE 索引表中查找相似环境下的NEE 来代替缺失数据[6]。通常选取光强和温度作为索引因子，光强以100μmol·m−2·s−1的间隔从0 渐增至2200μmol·m−2·s−1，温度以2℃的间隔从可能最低温度到可能最高温度，缺失NEE 数据用线性内插法生成。使用 R Package ‘REddyProc’sEddyProc_sFillLUT 命令建立季节索引表进行数据插补，记为LUT。

1.3.3 非线性回归法

非线性回归法（NLR）基于参数化非线性方程，通过建立一定时间内有效NEE 观测值与相关环境因子（如温度和光强）的经验方程，根据缺失时段的环境因子估算缺失的NEE[3,6,14]。通常，将日间与夜间的NEE 数据分开处理，使用呼吸方程来计算夜间NEE（等于夜间生态系统呼吸），使用光响应方程结合日间生态系统呼吸来计算日间NEE；进行回归分析的时段无明确限定。使用R Package ‘Nonlinear Least Squares’ nls 命令拟合Lloyd & Taylor 方程和Michaelis-Menten 方程进行数据插补，记为NLR。

呼吸方程，即Lloyd & Taylor 方程为[6,24]

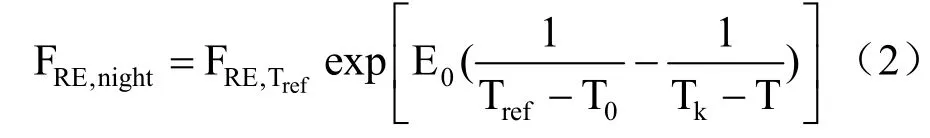
式中，FRE,night为夜间生态系统呼吸（等于夜间的NEE，μmol·m−2·s−1，以CO2物质的量计）；E0是常量，常设为309K；Tref是参考温度（K），一般为298.16K；FRE,Tref为参考温度下的生态系统呼吸（μmol·m−2·s−1，以CO2物质的量计）；T0是生态系统呼吸为0 时的温度（K）； T0为空气或土壤温度（K）。参数T0和FRE,Tref通过观测数据回归拟合得到。

光响应方程，即Michaelis-Menten 方程为[6,25]

式中，QPPFD为光量子通量密度（μmol·m−2·s−1）；α '为生态系统量子效率（μmolCO2·μmol−1quanta）；FGPP,opt是最佳光照条件下的总初级生产力（μmol·m−2·s−1，以CO2物质的量计）；FRE,day是日间的生态系统呼吸（μmol·m−2·s−1，以CO2物质的量计）。参数 α '和FGPP,opt通过观测数据回归拟合得到。

1.3.4 边际分布采样法边际分布采样法（MDS）是平均昼夜变化法和查表法的综合使用，在气温（Ta）、总辐射（Rg）和饱和水汽压差（VPD）观测数据均可用时，在一定的时间窗口（缺失数据前后14～28d）内，分别以2.5℃、50W·m−2和0.5kPa 的变异范围约束Ta、Rg和VPD 进行数据插补；在仅Rg 数据可用时，将插补的时间窗口缩小至前后14d；在气象观测要素全部缺失时，则使用平均昼夜变化法对缺失数据进行插补；若仍有缺失则扩大时间窗口重复上述步骤，直至完成对全部缺失数据的插补[10]。使用R Package‘REddyProc’ sEddyProc_sMDSGapFill 命令对缺失数据进行插补，记为MDS。

1.3.5 人工神经网络法

人工神经网络（ANN）是基于计算机网络还原人脑或生物神经的网络结构和激励行为的并行非线性计算系统[[7,26−28]，通过建立经验非线性回归模型进行数据插补。目前，较常使用的人工神经网络是在监督训练程序下能够还原各环境因子间复杂关系的误差反传、信息前馈神经网络（Feed-forward backpropagation neural network，BP 网络）。在气象样本数据信号（通常经过标准化处理转换为[0,1]）由输入层进入BP 神经网络各结点后，各输入变量都被乘以分配给该结点的权重值，并经转换函数反复修正各层神经元之间的连接权重，使误差评价函数最优，实现网络实际输出与期望输出的误差最小化。以气温（Ta）、饱和水汽压差（VPD）、总辐射（Rg）作为输入变量，以70%的数据作为训练集（training set）、15%的数据作为验证集（validation set）、15%的数据作为检验集（testing set），使用Matlab Neural Net Fit 工具箱构建具有10 个隐含神经元、基于Bayesian Regularization 的BP 神经网络来进行数据插补，记为ANN。

1.4 统计参数

使用决定系数（R2）、相对均方根误差（RRMSE）和平均绝对误差（MAE）评估各插补方法的性能。

式中， pi为各插补方法预测的 NEE（μmol·m−2·s−1），oi为实际观测的NEE（μmol·m−2·s−1），为各插补方法预测NEE 的均值（μmol·m−2·s−1），为实际观测NEE 的均值（μmol·m−2·s−1），均以CO2物质的量计；N 为样本数。

由于基准数据集中昼夜缺失比率不同，在对插补方法进行比较时，若将日间和夜间整合分析，白天和黑夜对统计指标的贡献权重的差异会影响最终的结果，带来一定的偏差。因此，单独计算和分析日间和夜间的统计参数。

使用 SPSS 25 对统计参数进行方差分析（ANOVA）和多重比较。使用Origin 2021 作图。

2 结果与分析

2.1 不同方法日间数据插补效果的比较

如图1a 所示，在5 类缺失情景下，不同方法插补所得日间NEE 与实测NEE 间的R2均在0.5 以下；NLR（非线性回归法）的R2最低，始终在0.2 以下；LUT（查表法）在连续1d 和3d 缺失情景下极差较小（极差在0.12 以下），在连续缺失达到7d 时极差明显增大（极差始终大于0.18）。MDV（固定窗口平均昼夜变化法）和MDC（可变窗口平均昼夜变化法）的R2在连续1、3 和7d 缺失情景下波动较小，结果相对稳定，在连续15 和31d 缺失情景下变异系数显著增大；MDS（边际分布采样法）和ANN（人工神经网络法）的R2在连续1、3、7 和15d 缺失情景下波动较为稳定（极差在0.2 左右），在连续31d 缺失情景下极差开始增大，分布更为离散，获得结果的稳定性趋于减弱。

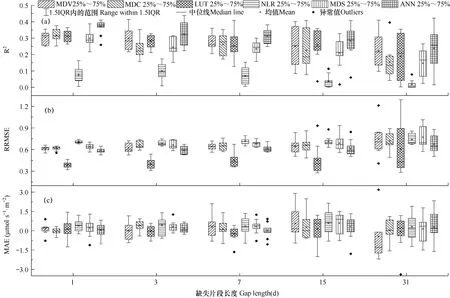
图1 五类缺失情景下不同方法插补所得日间NEE 数据集的统计参数（2017年3月1日−11月30日，Rg＞20W·m−2，0.5h 数据间隔）Fig.1 Statistical parameters of the daytime NEE datasets obtained by six gap−filling methods in five types of gap scenarios(Mar.1st-Nov.30th,2017,Rg＞20W· 0.5h data interval)

由表2可知，在连续1d 缺失情景下，ANN 方法的R2最高，NLR 方法的R2最低，与其它方法存在显著差异（P＜0.05）；在连续3 和连续7d 缺失情景下，NLR 方法的R2仍显著最低，ANN 方法的R2较高，但与MDV 方法差异不显著（P＜0.05）；当缺失达到连续15d 时，NLR 方法的R2最低，与其它方法差异显著（P＜0.05），而其它方法间R2差异不显著。随着缺失片段长度的增加，除MDV 方法外，各方法的R2均呈下降趋势，MDS 方法的R2在连续15d缺失与连续31d 缺失情景下的R2差异显著（P＜0.05）；MDC 和NLR 方法的R2在连续7d 缺失与连续31d 缺失情景下的R2差异显著（P＜0.05）；LUT和ANN 方法的R2在连续3d 缺失与连续31d 缺失情景下的R2差异显著（P＜0.05）；MDV 方法的R2始终无显著差异。

表2 五类缺失情景下不同方法插补所得日间NEE 数据集R2 多重比较表（Duncan 法）Table 2 The multiple comparison of R2 of the daytime NEE datasets obtained by six gap-filling methods in five types of gap scenarios (Duncan method)

如图1b 所示，在连续缺失≤15d 时，LUT 方法插补所得日间NEE 与实测值NEE 间的RRMSE（相对均方根误差）明显低于其它方法，平均值在0.4 左右，极差相对较小，分布较为集中，但在连续31d缺失情景下，极差显著增大，分布较为离散；MDV、MDC 和MDS 方法的RRMSE 在连续1、3 和7d 缺失情景下波动较小，在连续15d 和连续31d 缺失情景下极差显著增大；NLR 和ANN 方法的RRMSE 波动范围相对平稳，在连续31d 缺失情景下，极差有增大趋势，分布开始更为离散。

由表3可知，在连续1d 缺失情景下，LUT 方法的RRMSE 最低，NLR 方法的RRMSE 最高，与其它方法存在显著差异（P＜0.05）；在连续3d 和连续7d 缺失情景下，LUT 方法的RRMSE 仍最低，NLR方法的RRMSE 较高，但与MDS 方法差异不显著，与MDV、ANN 方法差异显著（P＜0.05）；当缺失达到连续15d 时，LUT 方法的RRMSE 较低，与其它方法有显著差异（P＜0.05），而其它方法间RRMSE差异不显著；当缺失达到连续31d 时，各方法间RRMSE 无显著差异。随着缺失片段长度的增加，MDV 和MDS 方法的RRMSE 呈增大趋势，连续1d缺失与连续31d 缺失情景下的RRMSE 差异显著（P＜0.05）；其它方法的RRMSE 差异相对不显著。

表3 五类缺失情景下不同方法插补所得日间NEE 数据集RRMSE 多重比较表（Duncan 法）Table 3 The multiple comparison of RRMSE of the daytime NEE datasets obtained by six gap-filling methods in five types of gap scenarios (Duncan method)

如图1c 所示，在连续缺失＜15d 时，各插补方法所得日间NEE 与实测值NEE 间的MAE（平均绝对误差）无明显差异，分布较为集中；在连续缺失31d 情景下，MDV 方法的MAE 出现较多异常值，各方法之间的MAE 开始出现分化的趋势。

2.2 不同方法夜间通量插补效果的比较

如图2a 所示，与日间通量插补结果不同，在5类缺失情景下，夜间通量插补所得NEE 与实测NEE间的R2普遍较小，不同插补方法的R2始终在0.2 以下。LUT（查表法）的R2始终很小，分布集中且趋近于0；MDV（固定窗口平均昼夜变化法）的R2相对稳定，随连续缺失片段的增加无明显变化；ANN（人工神经网络法）的R2均值相对较高，但始终存在较大波动，稳定性较差，随着连续缺失片段的增加分布趋于集中；在连续缺失片段增加到7d 时，各方法的平均R2趋于相等，差异越来越小；在连续缺失片段增加到15d 时，MDC（可变窗口平均昼夜变化法）、MDS（边际分布采样法）和NLR（非线性相关法）的R2趋于稳定。

由表4可知，在各缺失情景下，ANN 方法的R2较高，LUT 方法的R2较低，二者之间差异显著（P＜0.05）；在连续缺失片段长度大于3d 的情景下，ANN 与MDV、NLR 方法的R2的差异不再显著；在连续缺失片段达到15d 的情景下，ANN 与MDS 方法的R2出现显著差异（P＜0.05）；而在连续缺失片段达到31d 时，ANN 与MDC 方法的R2出现显著差异（P＜0.05）。随着缺失片段长度的增加，MDC、MDS 和ANN 方法的R2呈下降趋势，MDC 和MDS方法在连续7d 缺失与连续31d 缺失情景下的R2差异显著（P＜0.05），ANN 方法在连续1d 和连续3d 缺失与连续15 和连续31d 缺失情景下的R2差异显著（P＜0.05），MDV 与LUT 方法的R2始终无显著差异。

如图2b 所示，在各类缺失情景下，LUT 方法插补所得夜间NEE 与实测NEE 间的RRMSE（相对均方根误差）明显高于其它方法，平均值始终在0.9 以上，且极差相对较大，分布较为离散；NLR 和MDS方法的RRMSE 在连续1d 和连续3d 缺失情景下波动较小，在连续缺失达到7d 时分布开始趋于离散；与MDV 方法不同，MDC 和ANN 方法的RRMSE 波动相对平稳，在各缺失情景下具有相似的极差。

由表5可知，在5 类缺失情景下，LUT 方法的RRMSE 最高，与其它方法存在显著差异（P＜0.05）。除LUT 方法外，在连续缺失≤15d 的情景下，ANN方法的RRMSE 显著低于MDC 方法（P＜0.05），而在连续缺失大于31d 的情景下，各方法的RRMSE 差异均不显著。随着缺失片段长度的增加，各方法的RRMSE 差异无显著变化。

如图2c 所示，夜间不同方法插补所得夜间NEE与实测NEE 间的MAE（平均绝对误差）远低于日间；LUT 方法的MAE 始终为正，明显高于其它方法，且分布较为离散，在连续缺失1d 情景下极差约为其它方法的2 倍；在连续缺失片段长度达到7d 时，除LUT方法外，其它方法的MAE 开始出现较大的波动，分布趋于离散；在5 类缺失情景下，除LUT 方法外，其它方法的MAE 无明显差异；与其它方法相比，MDV 方法的MAE 更趋近于0，NLR、MDS 和ANN方法的MAE 趋近于负值。

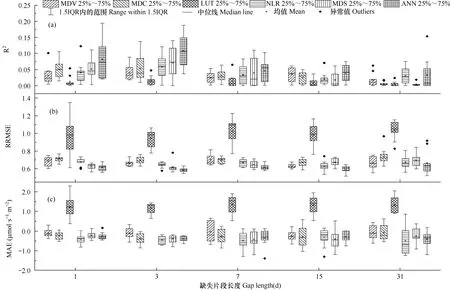
图2 五类缺失情景下不同方法插补所得夜间NEE 数据集的统计参数（2017年3月1日−11月30日，Rg≤20W·m−2，0.5h 数据间隔）Fig.2 Statistical parameters of the nighttime NEE datasets obtained by six gap-filling methods in five types of gap scenarios(Mar.1st-Nov.30th,2017,Rg≤20W·m−2,0.5h data interval)

表4 五类缺失情景下不同方法插补所得夜间NEE 数据集R2 多重比较表（Duncan 法）Table 4 The multiple comparison of R2 of the nighttime NEE datasets obtained by six gap-filling methods in five types of gap scenarios(Duncan method)

表5 五类缺失情景下不同方法插补所得夜间NEE 数据集RRMSE 多重比较表（Duncan 法）Table 5 The multiple comparison of RRMSE of the nighttime NEE datasets obtained by six gap-filling methods in five types of gap scenarios (Duncan method)

2.3 不同方法典型晴天日变化数据插补效果的比较

为探究不同方法在0.5h 尺度上日变化的插值效果，以在5 类缺失情景中均涉及的生长稳定的典型晴天2017年5月25日NEE 数据（数据缺失率为8%）为例，对比插补NEE 与实测NEE 的差异，分析各方法在不同缺失情景下对NEE日变化趋势的还原效果（图3）。

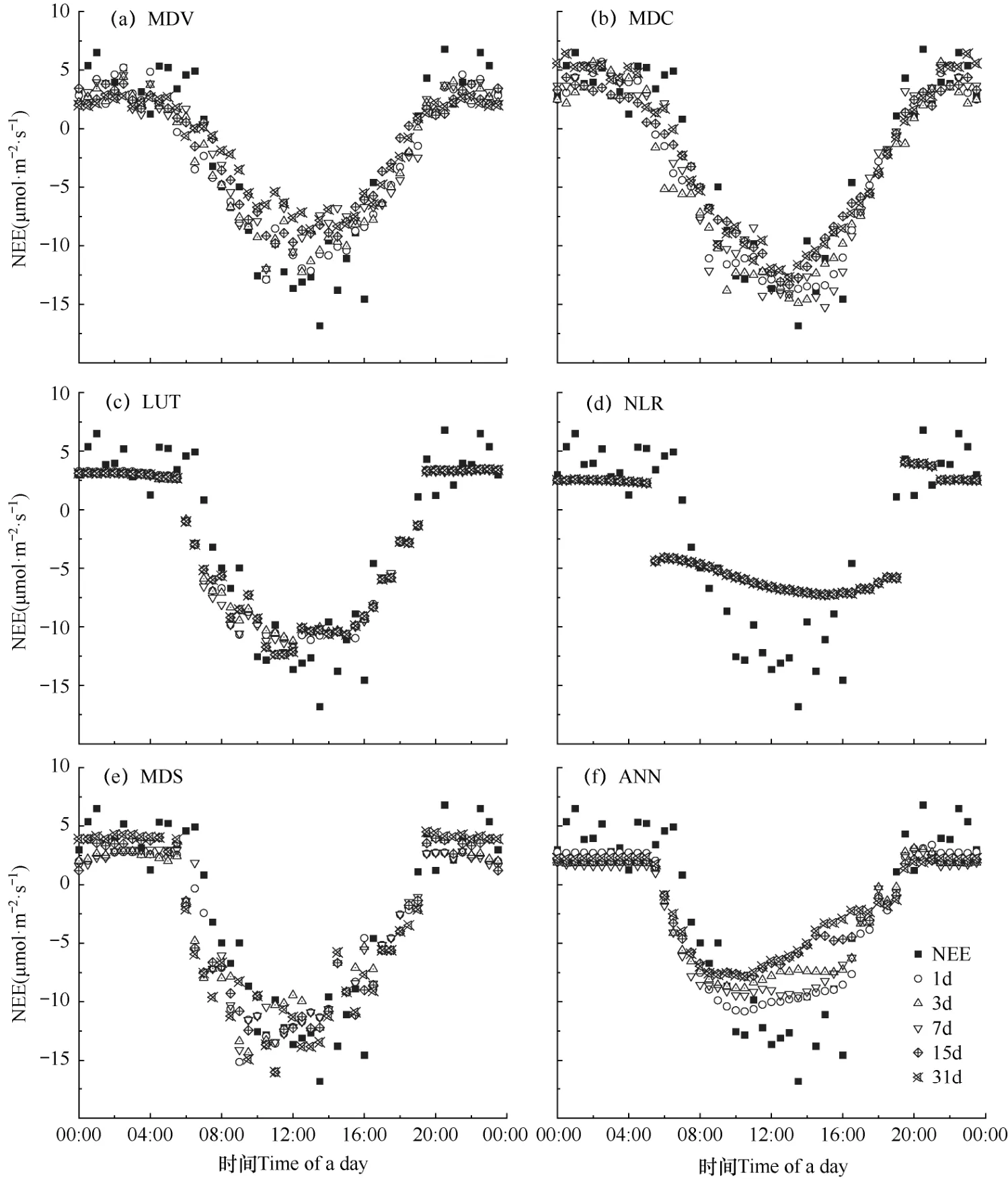
图3 典型晴天下不同插补方法在五类缺失情景下NEE 的日变化（2017年5月25日，0.5h 数据间隔）Fig.3 Variation curve of the daily change of NEE filled by six gap-filling methods under five types of gap scenarios in a typical sunny day (May 25,2017,0.5h data interval )

由图3可见，MDV（固定窗口平均昼夜变化法）在1d、3d 连续缺失情景下，对0.5h 尺度NEE 插值效果相对较好，但当连续缺失达到7d 时，对夜间0.5h尺度NEE 开始出现较为明显的低估，对日间0.5h 尺度NEE 开始出现较为明显的高估，不能准确预测日间CO2的吸收峰值。

MDC（可变窗口平均昼夜变化法）对0.5h 尺度NEE 插值效果相对最优，在不同连续缺失情景下均能较好地还原NEE 的日变化。

LUT（查表法）对夜间0.5h 尺度NEE 存在明显且稳定的低估，在不同连续缺失情景下无明显差异，对日间0.5h 尺度NEE 预测效果相对较好，在6：00−9：30 存在一定程度的低估，在10：00−16：00 存在一定程度的高估，使得日变化曲线在12：00−15：00时出现不明显的“上凸”现象。

NLR（非线性回归法）在不同缺失情景下，插补效果相对稳定，但对夜间0.5h 尺度NEE 存在明显低估，对日间0.5h 尺度NEE 存在明显高估，“U”型曲线不明显，对NEE日变化趋势的还原效果最差。

与MDV 和MDC 方法类似，MDS（边际分布采样法）能够在一定程度上还原夜间0.5h 尺度NEE 的波动，但还原效果会随着连续缺失片段长度的增加而降低；与MDV 和MDC 方法不同，MDS 方法对日间0.5h 尺度NEE 曲线的还原具有明显的左偏现象，在9：00 左右会出现一个极小值。

与LUT 和NLR 方法类似，ANN（人工神经网络法）对夜间0.5h 尺度NEE 预测相对较差，存在明显的低估，不能捕捉到夜间NEE 的波动。同时，ANN 方法对日间NEE 存在高估，预测NEE 最小值出现的时间比实际观测提前4h（由14：00 提前至10：00），与实际NEE 曲线相比在10：00−16：00存在明显“上凸”现象。随着缺失片段长度的增加，ANN 方法对夜间NEE 的低估和对日间NEE 的高估程度呈增加趋势。

3 讨论与结论

3.1 讨论

3.1.1 日间和夜间NEE 插补效果的差异

在对缺失NEE 数据进行插补时，日间和夜间插补效果存在显著差异，日间不同方法插补所得NEE数据与实测数据的R2明显高于夜间，RRMSE（相对均方根误差）明显低于夜间，插补效果明显优于夜间。

日间大气层结不稳定，热量交换频繁，对流作用较强，适合湍流交换，基本满足利用涡度相关观测系统进行通量观测的要求，经过数据质量控制后数据缺失较少。而夜间辐射冷却导致大气层结稳定，对流较弱，抑制湍流混合，涡度相关法通量观测结果较差，在剔除不满足通量观测条件的值后，往往会产生较多的缺失。同时，夜间经常发生平流、泄流效应，垂直方向上湍流运动倾向于向高频移动，以小涡运动占优势，开路式涡度相关系统传感器的分离等会造成观测仪器响应的不足，进而引起对夜间通量的低估，引入选择性系统误差[1]。在对NEE数据进行插补时，由于夜间可用样本数远低于日间，再加上夜间涡度相关法更倾向于低估NEE 的特性，使得夜间NEE 插补效果远低于日间。

3.1.2 不同插补方法NEE 插补效果的差异

不同插补方法的通量插补效果存在差异。不管是日间还是夜间，ANN（人工神经网络法）往往总能取得相对较好的插补结果，而NLR（非线性相关法）则相对表现较差；LUT（查表法）在日间的表现明显优于夜间；MDV（固定窗口平均昼夜变化法）、MDC（可变窗口平均昼夜变化法）和MDS（边际分布采样法）之间差异不显著。

与Moffat 等[29−30]的研究结果相比，本站点各方法对NEE 数据插补结果的R2相对较低。这可能与站点因素有关，本研究所用通量观测数据来源于山地丘陵林区，下垫面相对较为复杂，与农田和草地相比，对通量观测和数据插补的要求更高。

与Ooba 等[12,29,31]的结果类似，ANN 方法在连续缺失小于7d 时，数据插补结果的R2较稳定，高于其它方法，RRMSE（相对均方根误差）也相对较低，表现出较好的插值效果。ANN 方法对0.5h 尺度NEE的日变化还原较差，倾向于高估中午时分的NEE，一方面源于统计平均效应，另一方面也与输入参数的数量有关。除将总辐射、气温、饱和水汽压作为输入参数外，进一步增加土壤温湿度、风速等气象因子，并引入季节、生长期等非连续变量，可以进一步提高ANN 方法的精度。

NLR 方法在夜间通量插补中表现出较高的R2和较低的RRMSE，但在日间通量插补中则相反，与Moffat 等[29,32]NLR 方法在日间仍表现相对较好的结果存在差异。这可能与环境响应方程的选择和拟合方程时所选择的时段有关，不同物候期内栓皮栎人工林可能具有不同的光响应曲线，使用单月或更为精确的物候分期分段拟合环境响应方程或先将观测数据按温度分组后再利用环境响应方程进行回归模拟可能取得更好的插补效果。

LUT 方法在日间通量插补中表现出较高的R2和较低的RRMSE，在夜间通量插补中则相反。夜间可用实测NEE 的数据量远少于日间，绝对值也较日间低，在以季节为单位建立索引表时，较多的缺失会引起LUT 方法倾向于低估夜间NEE，带来难以避免的系统误差。

MDV、MDC 和MDS 方法具有一定的相似性，3 种方法均使用缺失数据周围一段时间内相关数据的均值来代替缺失值。但MDV 和MDC 方法并未考虑气象因素，MDS 方法则以气温、总辐射和饱和水汽压差梯度为限制条件；MDV 方法的窗口大小是固定的，MDC 和MDS 方法的窗口则是动态变化的。与Falge 等[6,29−30,32]的研究结果一致，在连续缺失15d以下情景时，MDV 方法技术具有较好的性能。但在统计平均效应的作用下，当连续缺失大于15d 时，MDV 方法会对日间NEE 产生高估。在数据连续缺失≤15d 时，MDV、MDC 和MDS 方法的R2和RRMSE 无显著差异，都能较好地还原0.5h 尺度NEE的日变化，但MDC 方法还原性能更好。

3.1.3 不同插补方法的适用性

不同NEE 插补方法的插补效果与数据缺失的持续时间有关。随着数据缺失时间的延长，各插补方法所得日间NEE 结果的稳定性一般会越来越差。各通量插补方法一般有其适用范围，即在一定限度的连续缺失时间内具有较好的插补效果，超过此限度后插补效果会显著降低。ANN（人工神经网络法）适用范围较广，即使是31d 的连续缺失，往往也能取得较好的插补效果，但在连续缺失少于7d 时能获得更好的结果；LUT（查表法）、MDV（固定窗口平均昼夜变化法）、MDC（可变窗口平均昼夜变化法）和MDS（边际分布采样法）的适用限度均在15d 以内；NLR（非线性相关法）表现相对较差，更适合7d 内的缺失插补。

Moffat 等[29,31]发现，ANN 方法在连续缺失少于7d 时能获得非常好的结果，在连续12d 缺失时，仍保持最优的插补效果。即使缺失时间延长至31d，ANN方法仍能取得较优的插补结果。与Falge 等[6,29−30,32]的研究结果一致，在缺失3～7d，甚至是12d 左右时，MDV 方法仍保持较好的性能，但在缺失时间继续延长时，其稳定性会大幅下降。Moffat 等[29−30]发现在连续缺失少于12d 时，MDS 方法具有较好的插补性能，与本研究MDS 方法在连续缺失达到15d 时插补性能出现下降且稳定性开始变差略有差异。这可能与站点特性有关，Moffat 等[29]分析对象为欧洲典型森林，而Du 等[30]关注的则是退化草地和玉米农田，与本研究所探讨的暖温带落叶阔叶林存在较大差异，站点的差异影响了不同插补方法的适用性及稳定性。

在对缺失NEE 数据进行插补时，当NEE 数据缺失＜15d 且气象数据不可用或缺失严重时，可以使用MDV 或MDC 方法；而当NEE 数据缺失＜15d，且气象数据可用时，则优先使用LUT、ANN 和MDS方法；在NEE 数据缺失≥15d 时，多次利用ANN 方法进行插值并取均值可能是比较好的选择。在关注NEE日变化趋势时，可优先使用MDC 方法。在数据缺失比较严重，可用数据量较少时，NLR 方法会有较大的误差。

除站点因素外，不同插补方法选取的时间步长和窗口大小的差异等也会影响缺失通量数据插补效果，进而影响各插补方法的适用性，本研究仅考虑了单一站点一年（除冬季）的通量数据，在构建人工缺失集时忽略了实际缺失的分布，所选插补方法在进行插补时所选用的时间步长和窗口大小也不尽相同，其结果可能并不适用于所有站点，但可为其它站点数据插补方法的选择提供参考。同时，部分通量数据的缺失源于降水、露水等异常天气的影响，通过上述方法插补所得的通量数据可能与实际通量有较大差异（显著高估），尤其是不考虑气象因素的MDV 和MDC 方法，要准确估计这部分通量，还需与闭路式涡度相关观测系统相结合，进行相应的数据校正研究。

3.2 结论

（1）在对缺失NEE 数据进行数据插补时，由于湍流稳态因素和开路式涡度相关观测系统传感器分离等的影响，日间插补效果显著优于夜间。由于插值策略的差异，不同插补方法的插补效果存在差异。ANN（人工神经网络法）插值效果总体较好，而NLR（非线性相关法）则相对表现较差；LUT（查表法）在日间的表现明显优于夜间，对夜间NEE 存在低估现象；MDV（固定窗口平均昼夜变化法）、MDC（可变窗口平均昼夜变化法）和MDS（边际分布采样法）之间差异不显著，但MDC 方法对半小时通量变化的还原性能更好。

（2）不同NEE 插补方法的插补效果与连续数据缺失的持续时间有关。随着连续缺失时间的延长，各插补方法所得结果的稳定性一般会越来越差。NLR 方法适用于气象数据完备、NEE 数据连续缺失少于7d 的情景；MDV 或MDC 方法适用于气象数据不可用或缺失严重、NEE 数据连续缺失少于15d 的情景，优先选用MDC 方法；LUT 和MDS 方法则适用于气象数据缺失较少、NEE 数据连续缺失少于15d的情景；ANN 方法适用性相对较广，可用于气象数据缺失较少、NEE 数据连续缺失长达31d 的情景。