基于机器学习方法的西安市数值模拟优化研究

李 娟， 尉 鹏， 戴学之， 赵 森， 张博雅， 吕玲玲， 胡京南

1.西安科技大学测绘科学与技术学院， 陕西 西安 710054 2.中国环境科学研究院大气环境研究所, 北京 100021 3.合肥市气象局， 安徽 合肥 230041

近年来，我国大气污染问题突出，引起社会高度关注，大气污染物对人体健康、大气能见度以及气候变化等都有重要影响[1-2]，因此对大气污染物进行预报、调控及污染机理分析成为当下亟待解决的科学问题. 大气化学模式是研究大气污染的重要工具，它以大气动力学为基础，考虑多种物理和化学过程，定量描述污染物的扩散和输送规律，但由于物理化学机理复杂、排放源不确定性等原因，使得数值预报结果存在不确定性[3-4].

为提高模式预报能力，结合数值模式与统计方法对模式预报结果进行统计修正的应用也较为普遍. 研究表明，利用机器学习方法可以有效提高模式预报准确率[5-6]，如利用多元线性回归(MR)、随机森林、BP神经网络、深度学习以及集合预报等方法对模式输出结果进行优化[7-9]. 王茜等[10]采用学习型线性回归方法对上海市ρ(PM2.5)数值预报结果进行修正，统计检验结果明显提高了ρ(PM2.5)预报效果；张岳军等[11]在BREMPS预报结果的基础上，结合MR、BP及多层递阶建立10 d滚动修正模型，PM2.5预报准确率升高；潘锦秀等[12]利用多元线性回归方法对北京市多模式系统(CMAQ、CAMx、NAQPMS)预报值和观测值进行集合预报，改进了模式的高估或低估现象. 但线性回归模型无法解决非线性问题，随着机器学习的发展，许多学者利用机器学习方法对污染物预报值进行订正优化，如张恒德等[13]基于CUACE、BREMPS、WRF-Chem模式预报产品，利用BP神经网络方法建立多模式集成预报模型，集成预报结果的归一化平均偏差及均方根误差均下降；戴李杰等[14]应用支持向量机(SVM)和粒子群优化算法建立PM2.5滚动预报模型，使得预报准确度提高；马井会等[15]结合WRF气象预报数据、地面及高空气象观测数据、ρ(PM2.5)观测数据，基于人工智能深度学习序列到序列的算法建立了上海市PM2.5统计修正预报模型，能有效提升ρ(PM2.5)预报精度. 机器学习可以很好地解决非线性问题，但目前大多数研究集中在单个机器学习模型对预报值进行优化，而对多种机器学习模型优化结果的对比以及模型对不同污染物优化效果评估的研究相对较少.

为提高CAMx污染物模拟值精确度，该研究以西安市为研究对象，基于CAMx模式污染物浓度预报数据、WRF模式气象要素预报数据以及环境空气质量监测国控点污染物浓度观测数据，利用6种机器学习优化模型(多元线性回归、岭回归、lasso回归、决策树、随机森林以及支持向量机)，对CAMx污染物浓度预报数据进行优化，旨在修正PM2.5、O3模拟值预报误差，以期为西安市大气空气质量预报预警方法做出改进.

1 数据与方法

1.1 数据来源

该研究所用气象数据来自中尺度气象模式WRF(V4.1)，其中WRF模式每日对初始场进行初始化，每次模拟时长为31 h，Spin-up时间设置为6 h. WRF模式中心点坐标为35 °N、110 °E，采用三层区域嵌套网格，水平分辨率分别为27、9、3 km，依次覆盖整个中国地区、陕西省和关中地区，与CAMx模式对应. WRF三层嵌套网格数分别为238×168、94×121、169×121，覆盖垂直层为35层. 气象背景场和边界条件资料来自NCEP(National Centers for Environmental Prediction)的再分析逐日资料FNL，分辨率为1°×1°，时间分辨率为6 h. 地形和下垫面输入资料分别来自USGS30全球地形和MODIS下垫面分类资料. 积云参数化方案采用Kain-Fritsch(new Eta)方案，边界层参数化方案采用Mellor-Yamada-Janjic(Eta)湍流动能方案，大气辐射方案为RRTM长波和云(Dudhia)短波辐射方案.

ρ(PM2.5)及ρ(O3)小时模拟值由综合空气质量模式CAMx提供，模拟时间为2019年1月1日—12月31日. CAMx模式采用Lambert投影，气相及液相化学机理分别为CB05、RADM-AQ；气溶胶热力学平衡模式为ISORROPIA，干沉降参数化方案采用WESELY89；水平平流及垂直扩散方案分别采用PPM、隐式欧拉方案. 模式第1次运行时模拟预测5 d的初始场，以消除初始条件的影响，后续初始场采用前一次的模拟结果，以消除排放源及初始条件累积误差.

人为源采用2016年MEIC (中国多尺度排放清单模型，Multi Resolution Emission Inventory for China)排放清单，分辨率为0.25°×0.25°；天然源运用陆地生态系统估算模型MEGAN[16]计算，整合、处理后的天然源、人为源排放清单共同输入到排放源处理模型SMOKE，转化为网格化的模式源排放文件.

西安市ρ(PM2.5)及ρ(O3)小时观测数据来自环境专业知识服务系统(http://envi.ckcest.cn/environment)，空气质量监测站点选择西安市长安气象监测站(站点号:57039).

1.2 模型建立

1.2.1特征提取及特征缩放

研究表明，气象因素可以影响大气污染物的稀释扩散、积聚清除，是影响污染物浓度的重要因素之一[1]，其中，较低的风速不利于污染物扩散，主导风向影响着污染物的区域输送，较高的相对湿度有利于颗粒物的吸湿增长，而高温则加剧了臭氧的光化学反应，同时天气形势的演变也是污染现象的一个重要原因[17-20]. 可见，风速、风向、相对湿度、温度、气压等气象因子对大气污染物浓度分布有较大影响. 结合西安市气象特点及相关研究[21-25]，该研究从CAMx模式模拟结果中分别选取PM2.5、O3小时质量浓度模拟值，从WRF中提取对应时间的温度、相对湿度、海平面气压、风速及风向小时值5个气象因子，共计6个因子作为建模训练的输入特征，其中回归目标值分别为相应时刻的ρ(PM2.5)、ρ(O3)小时观测值，并在数据集中随机选择80%作为训练集进行优化模型训练，20%作为测试集进行优化结果验证.

特征缩放可以消除各维数据之间的量级差别，提升分类算法和优化算法的性能，训练之前需要对数据进行标准化预处理[26-27]. 特征缩放的主要方法有归一化和标准化，其中，标准化方法使得特征值呈正态分布，利于训练阶段的权重更新；同时，标准化方法还可以保持异常值的信息，进一步减少异常值对算法的影响[27]. 标准化函数为

z=(x-u)/s

(1)

式中，x为训练样本，u为训练样本平均值，s为训练样本标准偏差.

1.2.2模型选取

在大气化学模式预报结果的基础上，利用机器学习模型对模拟结果进行优化，可以有效提高预报结果精确度[11]. 目前，机器学习模型中常用模型有多元线性回归[12]、岭回归[28]、lasso回归、决策树、随机森林[29]以及支持向量机[14].

多元线性回归(普通最小二乘法，ordinary least squares，OLS)通过寻找回归参数、回归常数及回归残差，使训练集预测值与真实回归目标值y之间的均方误差最小，利用训练集计算出特征值与观测值之间的函数关系，并将得出的方程应用于测试集，其回归方程表示为

Y=β0+β1X1+β2X2+…+βkXk+ε

(2)

式中：Y为模型预测结果;β0为回归常数;β1～βk均为回归系数;X1～Xk均为特征值，该研究中有6个特征值;ε为回归残差.

岭回归的预测公式与多元线性回归相同，通对预测模型进行显式约束，避免系数过拟合. Lasso回归通过正则化产生稀疏权值矩阵，使某些回归常数βk刚好为0，对特征进行自动化选择. 决策树通过反复切分数据进行回归或分类，与支持向量机、神经网络相比计算量大大降低，而且算法不受数据缩放影响. 随机森林通过随机的方式建立许多决策树并组成森林，是决策树的集成模型，随机森林相较于其他机器学习模型，可以量化的方式体现出模型参数对模型预报效果的影响，且预报效果较好、预报结果稳定. 支持向量机(Support Vector Machine，SVM)基于VC维理论和结构分析风险最小原则的理论，在解决小样本、非线性及高维模式识别中表现出许多特有的优势[30-32].

1.3 评估方法

对CAMx模式模拟结果与模型优化结果进行时间序列分析及统计检验. 统计检验指标选取均值偏差(MB)、标准化均值偏差(NMB)、平均相对偏差(MFB)、标准平均误差(NME)、平均相对误差(MFE)、均方根误差(RMSE)、平均绝对误差(MAE)及相关性系数(R)，计算公式见式(3)～(8). MB与RMSE反映了模拟值和观测值之间的偏差和误差大小，其绝对值越小，表明数值模拟结果与观测结果越接近. NMB、NME反映模拟值与观测值之间相对偏差大小，一般情况下，如果二者均小于50%，则认为模型模拟效果较好[33]. 当MFB≤±60%、MFE≤75%时，符合文献[34]中空气污染物模拟标准，则认为模式结果可靠；当MFB值在-30%～30%之间且MEF小于50%时，则可认为模式表现优秀，模拟结果在理想水平范围内.

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

2 结果与讨论

2.1 数值模拟结果

2.1.1WRF模拟结果

气象小时观测数据来自西安市长安气象监测站(站点号:57039)，利用观测数据对WRF模拟数据进行验证，检验参数包括均方根误差(RMSE)及相关性系数(R). 其中，温度及气压模拟值均与观测值的相关性较好，R分别为0.93、0.97，误差较小，RMSE值分别为2.96 ℃、2.88 hPa；而风速、相对湿度模拟结果均与其观测值相关性稍低，分别为0.70、0.67，RMSE值分别为1.38 m/s、23.1%. WRF模拟值误差分析可知，WRF整体模拟误差较小、精度较高，模拟结果可靠.

2.1.2CAMx模拟结果

为了解CAMx模式的预报特点，首先评估测试集中ρ(PM2.5)、ρ(O3)模拟值与观测值的相关性及时间序列分布. 由图1可见：ρ(PM2.5)模拟值与观测值的散点分布较为散乱，R为0.63；ρ(O3)模拟值与观测值分布较ρ(PM2.5)集中，R为0.78，模拟效果较好. 由图2可见：ρ(O3)模拟值与观测值时间变化序列一致，ρ(O3)模拟值与观测值较为接近，模拟效果较为理想；ρ(PM2.5)模拟值存在高估现象，模拟偏差主要出现在峰值阶段，而排放源的不确定性以及模式本身在多氧化过程和湿清除过程的不确定性对模式模拟结果有较大影响[34-35]. 分析其原因，一方面CAMx模式所用气象场来自WRF，WRF模拟气象场具有不确定性，而气象与污染物的相互反馈作用对污染物的分布有重要影响，从而造成CAMx模拟值偏差；另一方面，人为源排放量及排放类型变化速度快，而排放清单编制时效滞后也会带来预报的不确定性，同时MEIC清单本身存在误差，且排放清单分辨率低于模式网格分辨率，从而导致造成模式值的污染物空间分布具有差异性[36-39].

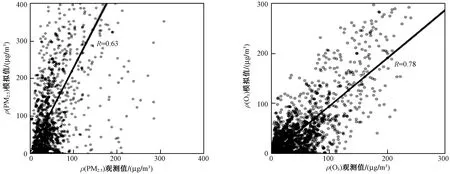
图1 ρ(PM2.5)、ρ(O3)模拟值与观测值的散点分布Fig.1 Scatter distribution of simulated and observed values of ρ(PM2.5) and ρ(O3)

表1为测试集中ρ(PM2.5)及ρ(O3)模拟值与观测值统计评估参数. 由表1可见：ρ(PM2.5)的MB值为74.07 μg/m3，表明模式值对观测值高估；NMB、NME值均大于1，表明模式值高估程度较高；MFB值较小而MFE值偏大，说明存在部分ρ(PM2.5)模拟值被低估现象；RMSE、MAE值分别为174.00、99.85 μg/m3，说明模式模拟结果误差及偏离程度较大.ρ(O3)整体模拟效果较好，其MB值为-3.99 μg/m3，说明模式值对ρ(O3)观测值整体略微低估；NMB值为-8.02%，表明模式值低估现象不明显，模式值与观测值较为接近；MFB、MFE值分别为-19.12%、52.86%，说明模拟结果可靠；RMSE、MAE值分别为37.11、26.81 μg/m3，表明模拟结果误差较小，模拟结果精度较高；R值为0.78，说明模拟值与观测值之间相关性较好. 总体来看，CAMx模式模拟结果能够较好地反映西安市ρ(O3)状况及变化趋势.

2.2 机器学习优化结果检验

2.2.1ρ(PM2.5)优化效果检验

该研究采用机器学习模型对PM2.5小时模拟结果进行优化，结果如图3所示. 由图3可见，对比ρ(PM2.5)观测值及相对应时间的CAMx模拟值、CAMx模型优化值发现，6种机器学习模型对CAMx的ρ(PM2.5)修正效果明显，相关性系数可提至0.70～0.78，散点由分散分布变为线性集中分布，其中，多元线性回归、岭回归及lasso回归优化后相关性系数提至0.70，决策树及支持向量机优化后R值分别提至0.72、0.74，随机森林优化后R值提至0.78.

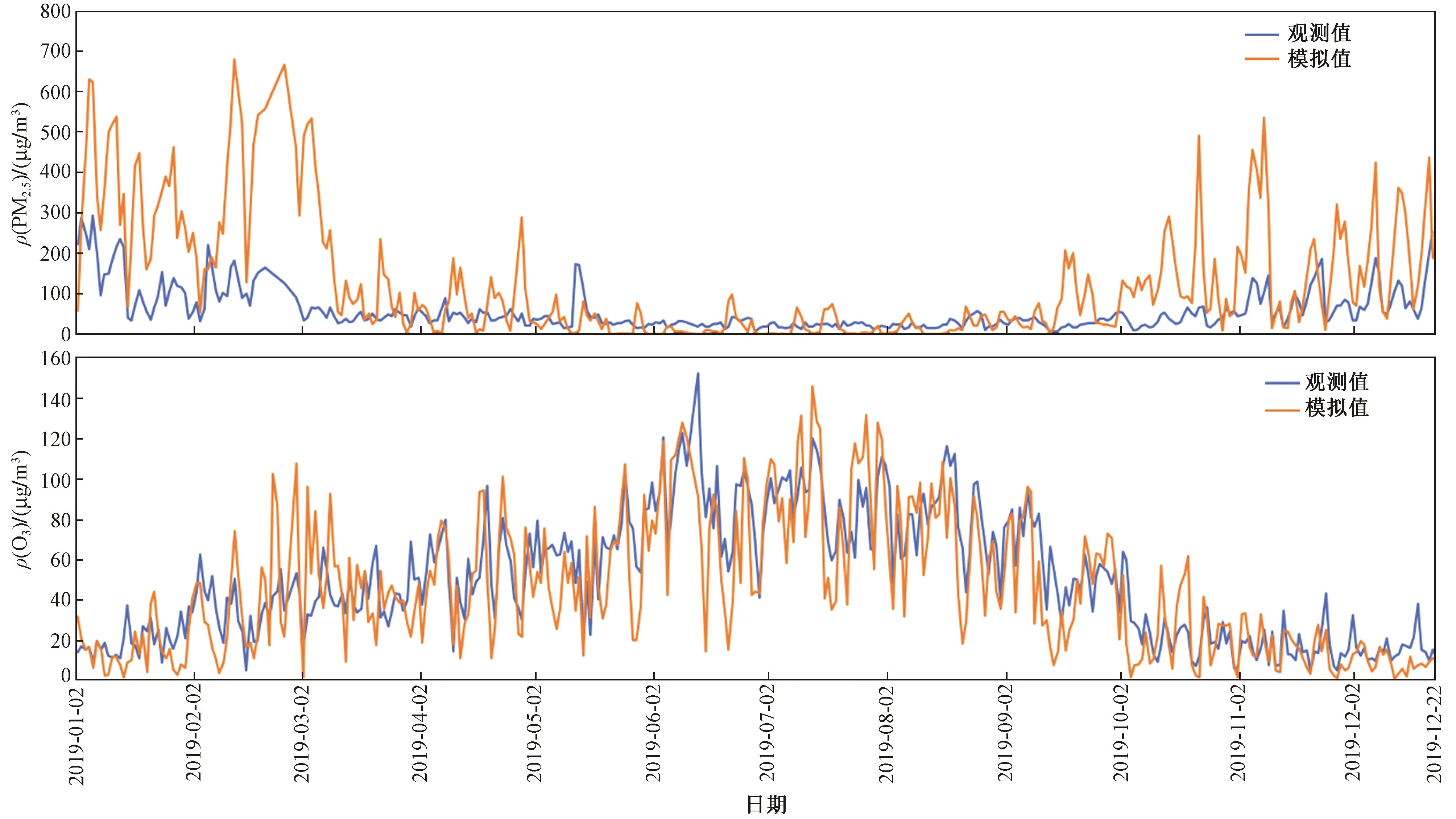
图2 ρ(PM2.5)、ρ(O3)模拟值与观测值的时间序列分布Fig.2 Time series distribution of simulated and observed values of ρ(PM2.5) and ρ(O3)

表1 ρ(PM2.5)、ρ(O3)模式值检验评估参数统计

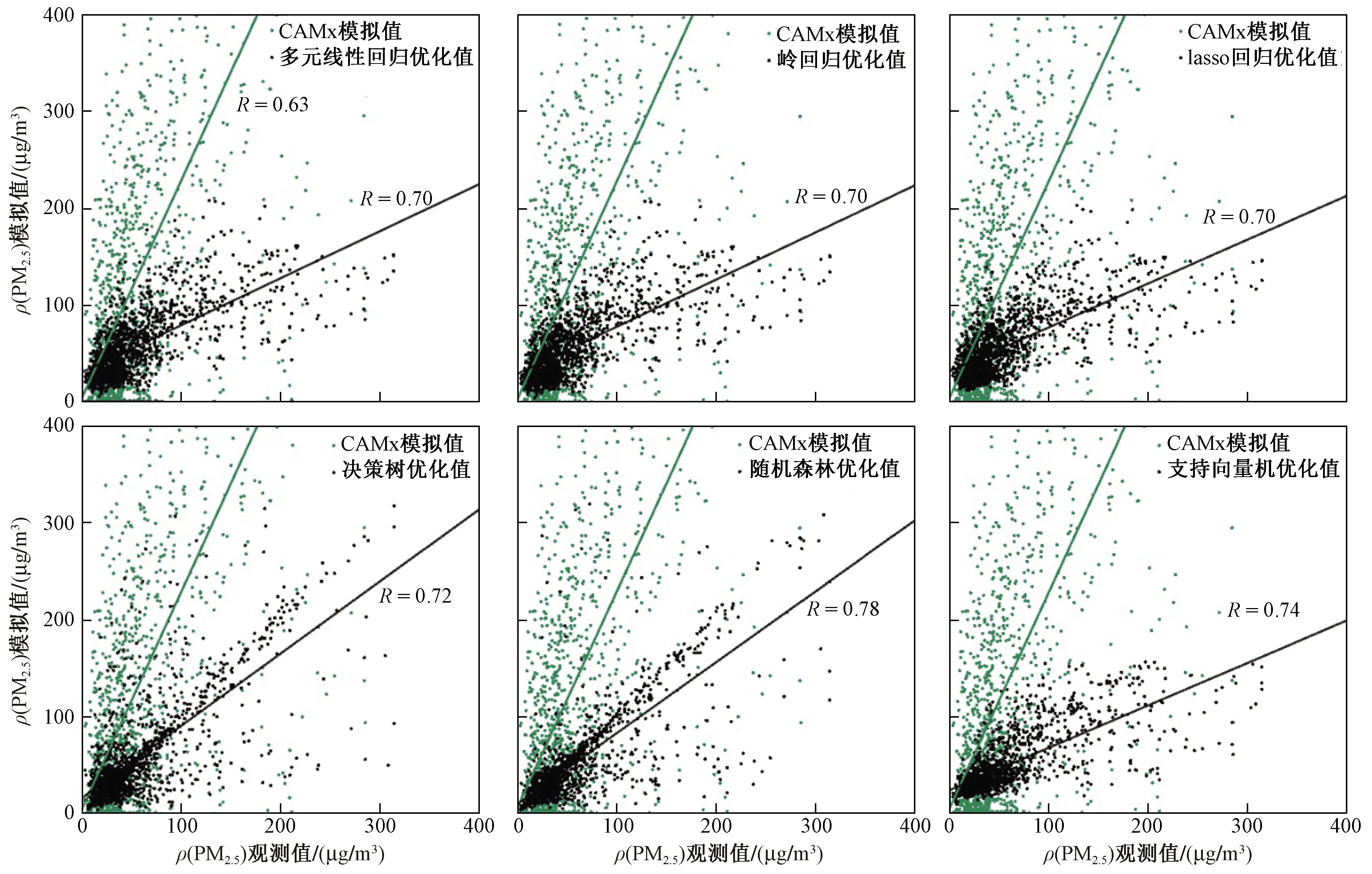
图3 ρ(PM2.5)优化结果散点分布Fig.3 Scatter distribution of ρ(PM2.5) optimization results

由表2可见，经机器学习模型优化后，各统计参数明显降低，ρ(PM2.5)订正结果显著. 多元线性回归优化后，MB、NMB、NME值分别从74.07 μg/m3、132.6%、178.75%降至1.37 μg/m3、2.5%、43.94%，模式值高估的现象得到明显改善，RMSE、MAE分别下降了137.12、75.31 μg/m3，离散程度大大降低；岭回归、lasso回归与多元线性回归的优化结果差别较小，模式优化结果达理想水平. 经决策树优化后，MAE、MFB、MFE值分别降至20.91、5.54、26.21 μg/m3，优化结果合理性提高；但RMSE为39.37 μg/m3，在6种模型中最大，说明优化值与观测值之间的偏差较大. 随机森林优化后MB、NMB值分别为-5.70 μg/m3、-10.21%，支持向量机的优化后MB、NMB值分别为-7.87 μg/m3、-14.09%，表明随机森林与支持向量机的优化结果均出现低估现象，其中支持向量机低估现象较为明显. 随机森林优化后RMSE、MAE值分别降至34.36、16.24 μg/m3，优化结果误差最小，检验指标达到要求标准，且该模型得到优化结果的相关性系数为0.78，R值在6个模型中最大. 综上，各优化模型有不同优势，综合分析可得，随机森林对ρ(PM2.5)的优化结果最优.

表2 ρ(PM2.5)优化模型评估参数统计Table 2 Evaluation parameters of ρ(PM2.5) optimization results

图4 ρ(O3)优化结果散点分布Fig.4 Scatter distribution of ρ(O3) optimization results

2.2.2ρ(O3)优化效果检验

由图4可见，6种机器学习模型对ρ(O3)优化效果表现优秀，相关性系数提高了6.4%～12.8%，优化结果分布更为合理，拟合度较高，其中，决策树、随机森林优化后R值分别提至0.83、0.85，多元线性回归、岭回归及lasso回归优化后R值提至0.86，支持向量机R值提至0.88.

结合表3的ρ(O3)优化结果发现：6种机器学习模型对ρ(O3)的优化效果理想，ρ(O3)模拟结果误差减小. 多元线性回归及岭回归对ρ(O3)优化效果一致，NB、NMB值均较小而NME值均较大；同时，MFB、MFE值分别为-17.27%、68.25%，对ρ(O3)部分数据有低估现象. Lasso回归MFE值降至47.54%，优化结果合理性提高. 随机森林的MB及NMB值均最大，低估现象较明显. 决策树RMSE值为28.82 μg/m3，误差最大，R值为0.83，小于其他5种优化模型，优化性能相对较差. 与其他5种机器学习模型相比，支持向量机优化后的RMSE、MAE值分别为23.76、17.40 μg/m3，预测值与观测值之间偏离程度低、误差小，MB、NMB、NME值较为合理，MFB、MFE值差异小，且拟合程度最好. 综上，支持向量机对ρ(O3)优化结果更为合理.

表3 ρ(O3)优化模型评估参数统计Table 3 Evaluation parameters of ρ(O3) optimization results

2.3 机器学习优化效果评估

2.3.1优化原理分析

CAMx模型的计算过程实质上是求解每个网格中每种污染物的物理化学变化连续方程，连续方程通过分子分裂法积分，进而计算每个主要过程(包括排放、平流、输送、扩散、去除和化学反应)对每个网格单元格内污染物浓度改变的独立贡献，模型核心表达式[40]：

(11)

2.3.2优化效果评估

图5为ρ(PM2.5)及ρ(O3)观测值、CAMx模拟值及优化模型优化结果分布对比. 由图5(a)可见：ρ(PM2.5)的CAMx模拟数据分布离散，与观测值差异较大，经机器学习模型优化后，CAMx模拟数据高估现象明显改善，数据分布形态与观测值更为接近. 对比ρ(PM2.5)观测值，多元线性回归、岭回归、lasso回归及支持向量机的优化结果对高浓度观测值出现低估现象，决策树优化后对高浓度观测值略有高估，而随机森林优化结果与观测值形态分布最为接近. 由图5(b)可见：与ρ(O3)观测值相比，CAMx模拟值出现峰值高估、整体低估现象，经机器学习模型优化后CAMx模拟数据整体更加符合观测值分布. 多元线性回归、岭回归、lasso回归优化后，ρ(O3)观测峰值被低估、ρ(O3)平均值提高，与观测值数据分布存有差异；随机森林优化后改善了观测峰值浓度被高估或低估现象，但整体ρ(O3)值偏低；决策树优化结果与ρ(O3)观测值整体较为接近，但其误差较大；支持向量机对ρ(O3)峰值略有低估，但优化结果与观测值最为接近.

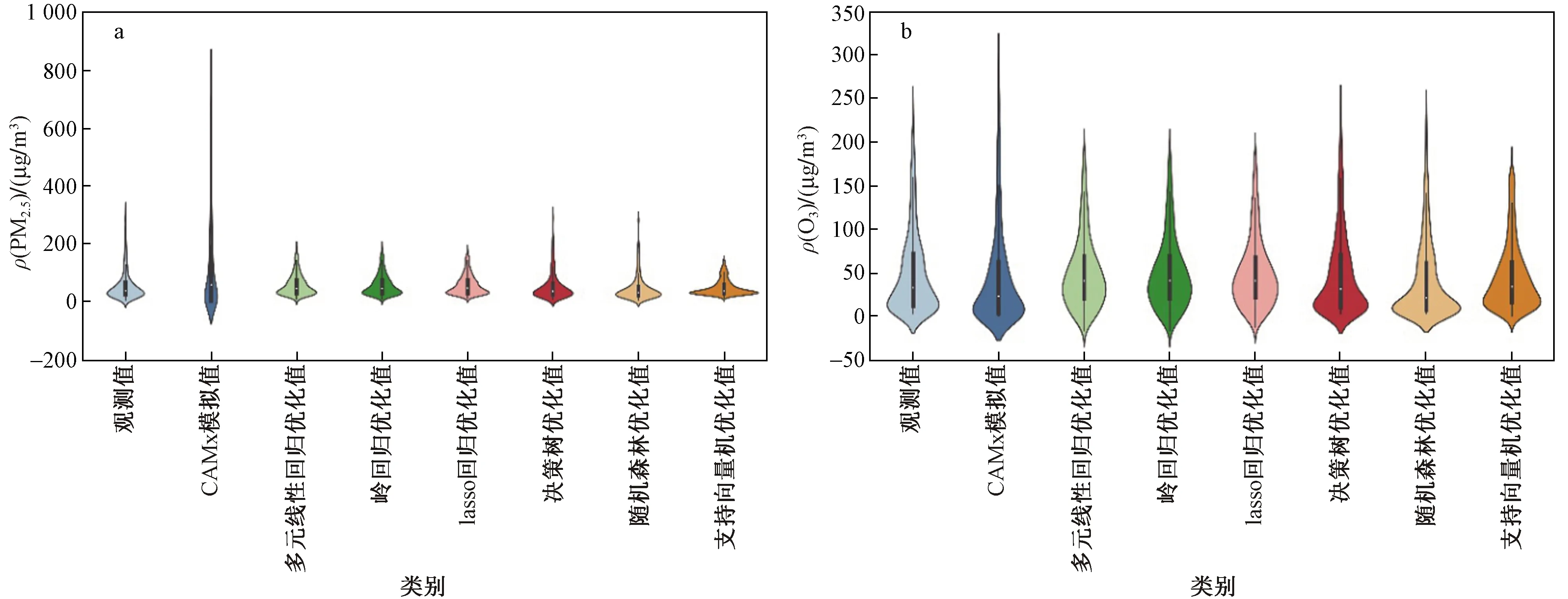
图5 ρ(PM2.5)、ρ(O3)模拟值与优化值统计分布对比Fig.5 Statistical distribution comparison of simulated and optimized values of ρ(PM2.5) and ρ(O3)

各优化模型对ρ(PM2.5)、ρ(O3)优化结果精确度提高率如表4所示. 优化前，ρ(PM2.5)的CAMx模拟值与观测值之间的RMSE为174.00 μg/m3(见表1)，CAMx模拟结果优化后，RMSE大幅降低，预报精度整体提高了77%～80%，其中经随机森林优化后的ρ(PM2.5)精度提高了80%，对ρ(PM2.5)的CAMx模拟值优化效果最好. 优化前，ρ(O3)的CAMx模拟值与观测值之间的RMSE为37.11 μg/m3(见表1)，CAMx模拟效果较ρ(PM2.5)模拟效果要好，机器学习模型优化后的预报精度提高了22%～36%，其中支持向量机优化效果最好. 对比各机器学习模型对ρ(PM2.5)与ρ(O3)的优化结果发现，决策树对ρ(PM2.5)和ρ(O3)的优化效果均较差；随机森林对ρ(PM2.5)的优化效果最好，但对ρ(O3)优化效果较差；多元线性回归、岭回归及lasso回归对ρ(PM2.5)的优化效果较差，但对ρ(O3)的优化效果较好.

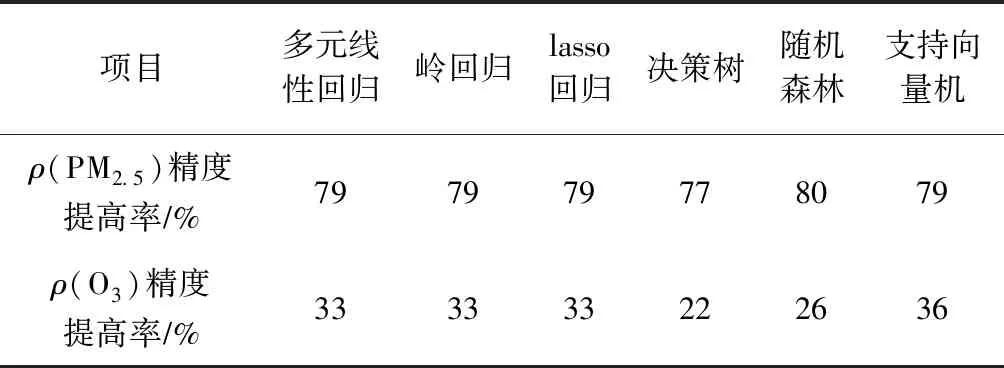
表4 ρ(PM2.5)、ρ(O3)优化模型结果精度提高率Table 4 The accuracy improvement rate of ρ(PM2.5) and ρ(O3) optimization results

3 结论

a) 2019年西安市污染物模拟浓度评估结果表明，CAMx模式在一定程度上能够反映ρ(PM2.5)、ρ(O3)的变化趋势，由于排放源滞后、模式分辨率较低等原因，使预报结果存在系统性偏差，ρ(PM2.5)、ρ(O3)模拟均方根误差分别为174.00、37.11 μg/m3；其中ρ(PM2.5)的CAMx模拟值对观测值出现高估现象，高估现象主要出现在ρ(PM2.5)峰值阶段，ρ(O3)的CAMx模拟值对观测值则略有低估.

b) 利用机器学习模型对CAMx模拟结果进行优化后，ρ(PM2.5)模拟值与观测值的相关性系数提至0.70～0.78，ρ(O3)模拟值与观测值的相关性系数提至0.83～0.88；不同优化模型修正程度不同，其中随机森林对ρ(PM2.5)优化后，其结果的稳定性和修正趋势整体优于其他方法，优化后精度提了80%，但对ρ(O3)模拟值优化效果相对较差；而支持向量机对ρ(O3)模拟值优化结果最接近观测值，优化后精度提高了36%.