旋笛式气动声源的声传播模拟及其计算结果分析
赵智丰,柏文文,时 洋,魏加华,*
(1.青海大学水利电力学院,省部共建三江源生态与高原农牧业国家重点实验室,青海大学,青海 西宁 810016;2.清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
旋笛式气动声源是一种以压缩空气为能源的大功率调制气流声源。因其具有气声转化效率高、输出功率大及声波波形控制能力强等特点,成功应用于多个领域。关于旋笛式气动声源的研究,20世纪70年代,Meyer[1]以准稳态简化为基础,对气流声源进行了严格的计算。马大猷[2]在这一基础上提出了适用于工程计算的近似理论,为研究大功率调制气流声源提供了理论基础。吴建星等[3]利用CFD软件对气动声源的内部流场进行了模拟,提出了谐振管内“气体活塞柱”的概念,进一步阐释了旋笛式气动声源的发声原理;为提高气动声源的发声强度,白春华等[4-5]对变截面、等截面和双曲型谐振系统进行了实验研究,发现变截面、双曲型谐振系统的发声强度均高于等截面的谐振系统;王鹏等[6]对旋笛式气动声源不同形状喷口的换能效率进行了数值计算,得出“异形喷口”换能效率更高,声功率更大;曹炯玮等[7]提出了声波传播与海拔之间的规律;时洋等[8-9]将计算流体动力学和离散元进行耦合(CFD-DEM),提出强声场作用会提高粒子团聚性;柏文文等[10]通过自主搭建的室内实验平台,研究了不同声波频率、声压级、声场行程、雾化通量对粒子团聚的影响效果。现阶段对于旋笛式气动声源的研究主要集中在气流声源的发声原理、结构稳定及声波作用下微粒的力学行为和物理过程等方面,对气动声源的声波传播规律的研究相对较少。鉴于此,本文利用COMSOL软件对旋笛式气动声源200 m范围内的声场进行模拟,研究6.3~200 Hz频段内1/3倍频程下各频率声场数值分布,并与室外实验所测量声压级进行对比。本研究的声波传播特性,对旋笛式气动声源的应用及其设计具有一定的借鉴意义。
1 旋笛声传播模拟与实测方案
1.1旋笛式气动声源本文中使用的旋笛式气动声源如图1所示。主要由发声器、外部电机、渐变谐振管和喇叭构成。其中发声器由定子和动环组成,定子包括渐缩进气口和喷口,动环上等间距有三个和固定喷口面积相等的圆孔,如图2所示。高压气流经定子内的流道到达喷口时,动环在外部电机的带动下高速转动进而周期性改变喷口处的截面面积,在谐振管内形成气体活塞柱。谐振管出口处周期性喷出气流引起空气谐振,形成强噪声,并经谐振管和拢声喇叭辐射到外场空间中。
1.2模拟计算方法流体中的声传播方程是由流体流动的控制方程(连续性方程、纳维斯托克斯方程、能量守恒方程、状态方程等)派生而来,压力声学中假定流体流动是无损且绝热的,本次仿真计算中流体模型选取“大气衰减”模型,控制方程如下式所示:
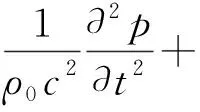
(1)
式中:ρ0表示空气密度,c表示空气中的声速,p表示声压。
1.2.1 声场模型概化及边界条件 本文重点研究声场在广泛空间领域中的传播过程,旋笛式气动声源内部发声单元附近的声波传播过程可以忽略,故略去发声器、外部电机等结构,只保留旋笛式气动声源的谐振管和喇叭。以谐振管底面圆心为定点,建立半球形声场。如图3所示,声场的远场边界处需添加完美匹配层(8 m)用来吸收远场声波,防止声波在数值外边界发生任何反射。此外,旋笛高度为3.4 m,综上所述,声场半径确定为211.4 m。
图3中所建立的声场模型是以旋笛式气动声源的谐振管和喇叭的中心线为轴线的轴对称模型,为节约计算资源,对三维声场进行剖切,得到对称的二维计算模型(图4)。在二维声场模型中,地面、谐振管和喇叭均简化为线形硬边界单元,渐变谐振管出口上边界采用“向内法向加速度”边界模拟声源,如下式所示:
(2)
式中:qd表示偶极声源;an(t)表示边界加速度的声信号。采用声压级SPL量化声波强度,如下式所示:
(3)
式中:pref表示参考压力,空气中取20 μPa,p0表示声压的振幅,与声速U0的振幅有关,如下式所示:
U0=p0/ρc
(4)
式中:ρ和c分别表示空气介质的密度和声速。
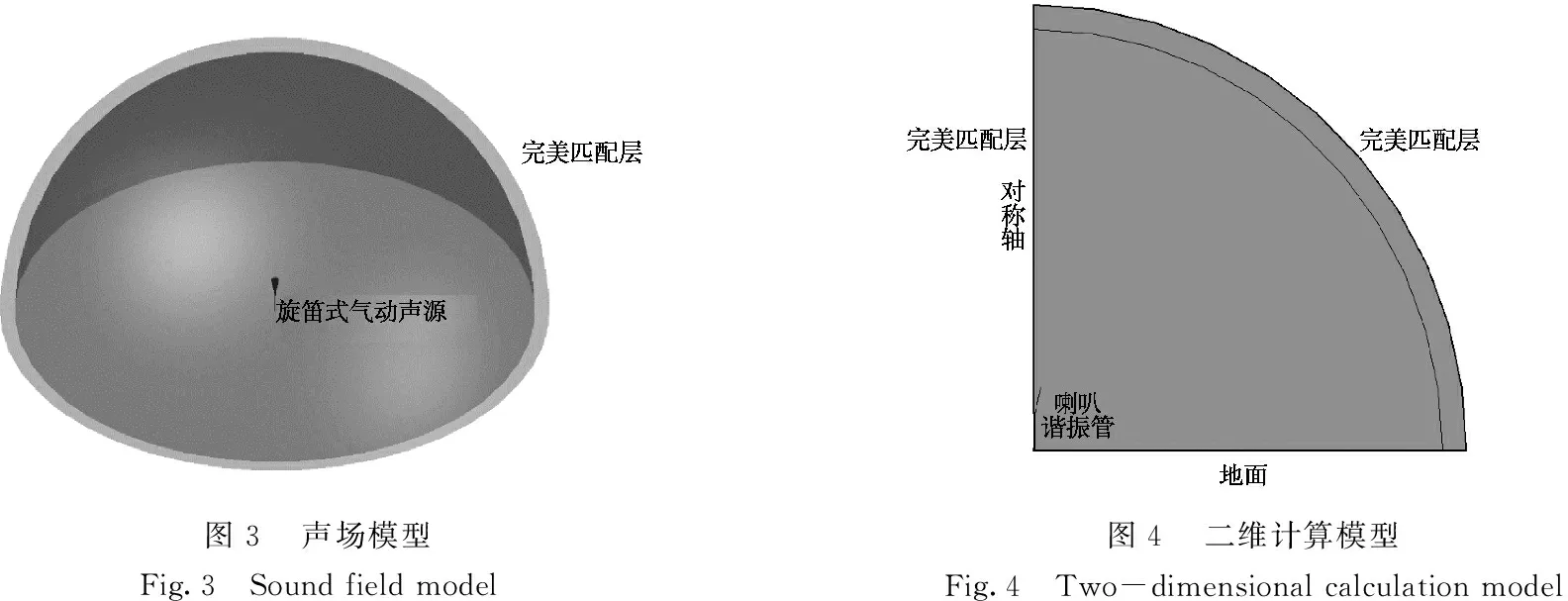
图3声场模型Fig.3 Sound field model图4二维计算模型Fig.4 Two-dimensional calculation model
1.2.2 参数设置及网格划分 利用COMSOL软件中的“压力声学—频域”模块对声场进行计算。声场中的流体材料选取内置的“空气”材料。求解器选用稳态求解器,计算频率取“6.3~200 Hz”频段内的1/3倍频程。
本数值模型采用自适应三角形网格进行划分,为了刻画声波传播过程,要求每个波长上最少5个网格,因此网格的“最大单元尺寸”设定为“空气中声速/最大研究频率/5”。共划分域单元794 460个,边界元3 160个。
1.3实测验证为验证仿真计算的准确性,在青海省海西蒙古族藏族自治州德令哈市实验基地(37°28′34.03″ N,96°48′54.76″ E)进行外场声场测量。
1.3.1 测量方案 测量时,以无风晴朗天气为最佳。为与数值模型保持一致,沿实验基地东西走向取纵剖面,在以旋笛气动声源的喇叭口中心及向其东、西偏移10 m处的测点为基点的3条垂线上进行声压级测量,每条垂线上选定10、20、40、50、80、100、150、160、200 m九个测量点。测量设备采用Ⅰ级声级计(BSWA308),测量范围为6.3~20 000 Hz。选用“1/3倍频程”模式进行测量,测量时将声级计固定在无人机(大疆 M600Pro)的底座上做垂直起降,根据无人机遥控器指示确定无人机的飞行高度,当飞行高度达到测点位置时,悬停在测点位置上并记录无人机飞行时间以确定声级计测量数据。
1.3.2 数据处理 在处理数据时,与模型计算频率保持一致,取6.3~200 Hz频段内各频率的声压级,根据下式计算出总声压级:
(5)
式中:Lxeq代表6.3~200 Hz的总声压级;N代表6.3~200 Hz频段中1/3倍频程所取的频率个数;Lzfi代表“z计权下”的各频率声压级。
测量方案中以无人机搭载声级计的方法进行高空测量,故在后处理时需要将无人机的背景噪声通过式(5)进行去除。
2 结果与分析
2.1模拟结果将计算结果做对称操作,得到6.3~200 Hz频段中1/3倍频程下典型频率声压级等值线分布图(图5)。从图中可以看出,当频率在6.3~12.5 Hz时,因为频率较小,此时的声波波长远大于旋笛尺寸,声波以较为规则的球面形式进行传播;当频率在16~20 Hz时,声波波长大于旋笛尺寸,声波受到喇叭边界影响,传播过程中呈现散射现象;当频率在25~200 Hz时,声波受到喇叭拢声作用以“集束”的形式向外场传播,并在近地面处因声波干涉叠加形成“条纹”状声波结构。当声波频率越高,即波长远低于声源设备尺寸时,因声波干涉叠加所产生的“条纹”状声波越多。
为探究“条纹”状声波波形对声波传播的影响,以喇叭中心点和偏离中心10 m处的点为基点做高度为200 m的垂线1和垂线2,如图6所示。在垂线1和垂线2上以1 m为间隔区200个测点,提取各测点不同频率的声压级,并利用式(5)计算出两条垂线上各测点的总声压级。垂线1和垂线2上的总声压级衰减趋势如图7所示。对垂线1上各测点的总声压级的数据进行非线性拟合,得到下式关系:
SPL=72.11×h-1.112+128.4
(6)
拟合函数的Adjusted R-square(校正决定系数)为0.996 2,呈指数形式衰减。垂线2上的总声压级呈现先增大后减小的趋势,且在10.4 m达到峰值130.75 dB。
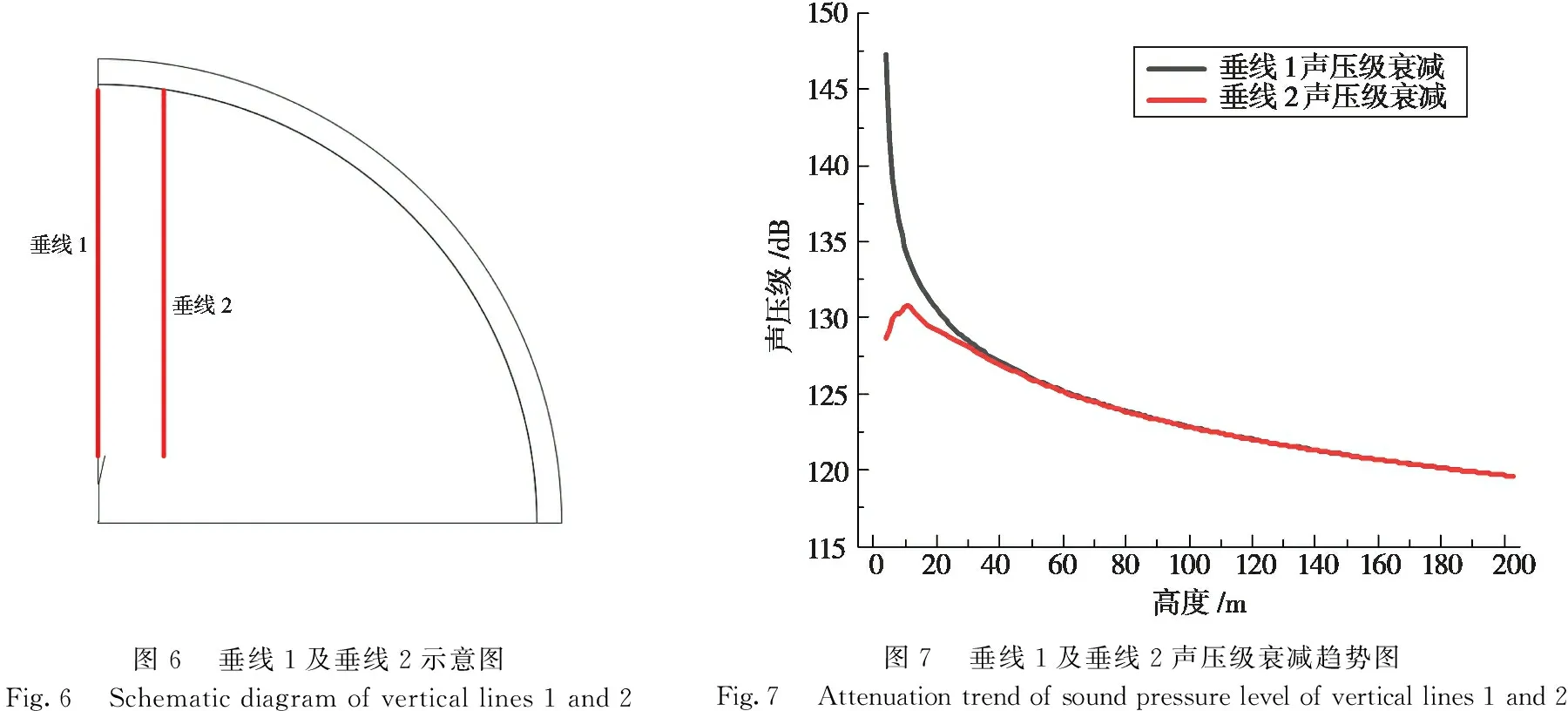
图6垂线1及垂线2示意图Fig.6Schematic diagram of vertical lines 1 and 2图7垂线1及垂线2声压级衰减趋势图Fig.7Attenuation trend of sound pressure level of vertical lines 1 and 2
2.2 实测结果
按照实测验证方案,对实验基础测量的原始数据进行处理后获得旋笛式气动声源在中心处及东、西两侧10 m处的垂线上声压级衰减数据,如表1所示。
对表1中心处垂线上声强信号进行拟合,得到下式关系:
SPL=148.6×h-0.063 39
(7)
拟合函数的Adjusted R-square(校正决定系数)为0.968 9,呈现出较好的指数形式衰减。东、西两侧垂线上的声压级均呈现出先增大后减小的趋势,和模拟结果的趋势相同,东10 m垂线上声压级在50 m处达到峰值114.66 dB;西10 m垂线上声压级在20 m处达到峰值109.15 dB。
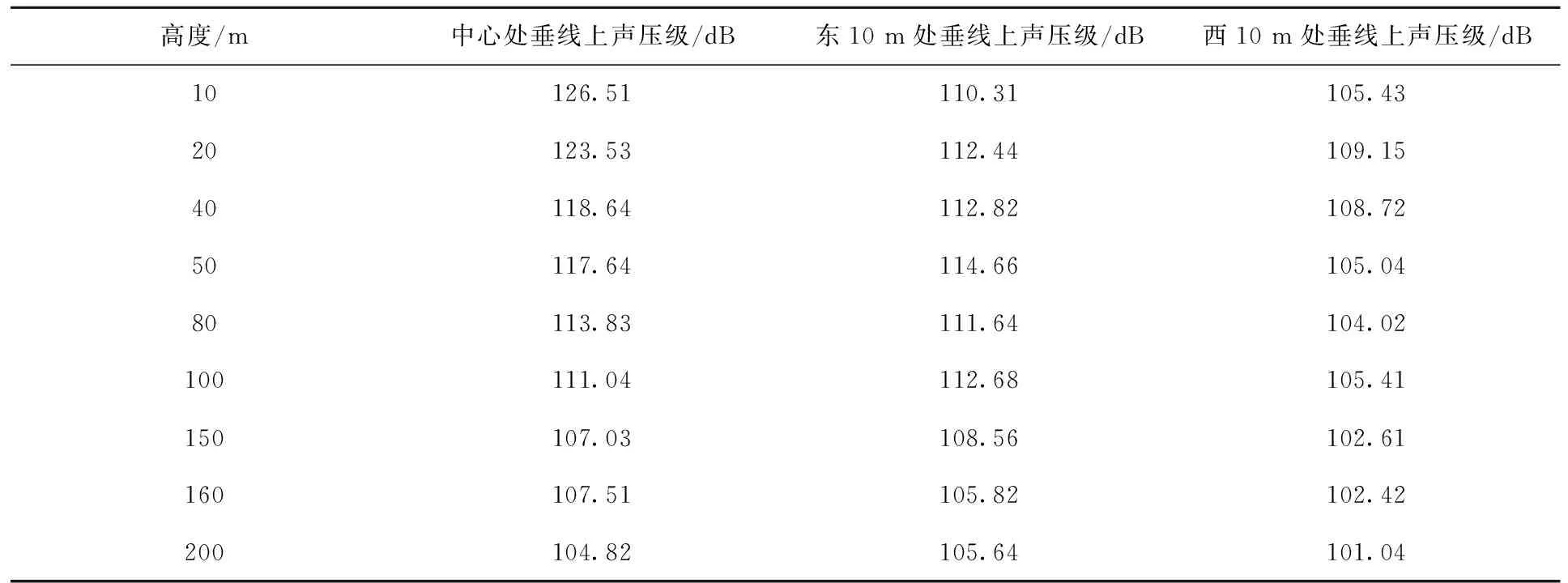
表1 垂线声压级衰减实测数据Tab.1 Measured data of attenuation of vertical sound pressure level
2.3 模拟值与实测值对比分析
从式(6)和式(7)可以看出,在半自由场中,以声源设备喇叭口中心点为基点垂线上的声压级是以指数形式递减的。从图5可以看出,在喇叭的作用下,当声波波长接近于或小于等于声源设备尺寸时,会出现“集束”作用,并在近地面形成指向声源设备的“条纹”状声波,且频率越大,“条纹”越多。通过实测数据和模拟结果的对比分析,可以认定此种“条纹”状声波会导致偏离声源设备喇叭口中心点的垂直面上近地面的声压级随高度的增加,呈现出先上升后下降的趋势。
在偏离声源设备喇叭口中心处垂线上的声压级衰减,实测值和模拟值均呈现出先上升后下降的趋势,不同之处在于实测值的峰值出现在20 m左右,模拟值的峰值出现在10.4 m,实测值与模拟值的峰值出现位置相差10 m左右。原因可能是在实际测量中,设备摆放的下垫面,喇叭壁面都不是完全反射的;且旋笛式气动声源的周边还摆放有其他设备(如空气压缩机等)会影响到近地面的声场分布。在后期工作中应当以“阻抗边界”来定义边界条件,同时将其他设备也进行建模,尽量做到数值模型与实测边界条件一致。
实测值在中心处垂线上200 m的距离声压级衰减值为21.7 dB,模拟值的声压级衰减了14.5 dB,模拟值的声压级衰减比实测值低7.2 dB。原因可能是在实际测量中,大气环境(气压,温度,风速等)不稳定的,在模拟中并没有考虑到大气环境的变化。在后期的工作中将考虑这一因素的影响。
3 结论
本文通过对旋笛式气动声源的发声、传声过程开展数值模拟,并结合实地测量数据,得到以下结论:
(1)当声波频率对应的声波波长远大于声源设备尺寸时,该频率下的声波在半自由场中以较为规则的球面形式传播;当声波频率对应的声波波长接近于或小于等于声源设备尺寸时,会出现“集束”作用,并在近地面形成指向声源设备的“条纹”状声波,且频率越大,“条纹”越多。
(2)声源设备喇叭口中心点处垂线上的声压级是以指数形式递减的;近地面指向声源设备的“条纹”状声波是导致偏离声源设备喇叭口中心的垂线上声压级出现先上升后下降的原因。
(3)实测声压级与模拟声压级的变化趋势相同,但是模拟结果比实测值低,这是因为模拟环境参数与现场环境参数不同而导致的。
本研究可以在一定程度上表征旋笛式气动声源声场的分布规律,对旋笛应用及其设计具有一定的借鉴意义。

