基于深度循环神经网络的大规模风力发电功率预测

向 勇, 王一军, 孔寅恪

(中南大学 自动化学院,湖南 长沙 410083)

1 引言

风电作为未来清洁能源的一种，应用前景广大，但风电输出的独特波动和间歇性，成为制约其快速发展的因素之一。大型风电场功率波动容易引起电网运行和调度较大的波动，尤其是风力发电特殊的防峰调节特性，造成电网调度与管理的难度。随着风电场在电力领域的不断增加和扩容，为保证电网平稳运行，发电站通过限制风力发电产量的办法进行管理与协调，难以适应后续发展。风能的随机性和波动性等难以控制因素，进一步导致了风力发电机运作稳定性差、功率波动、谐波污染、电压波动、电流异常、回路异常等问题，供电网络规模越大，对系统性能影响越大[1-3]。准确预测风力发电的输出功率，可以减少频率调制和峰值调节带来的压力，降低电力系统的波动及异常，提高电力系统对风力发电的兼容和提升能力[4-5]，降低运行成本，扩大风电覆盖面，提高风电场使用率、稳定性和安全性，是保证电网高效运行、促进清洁能源发展的有效措施之一。

本文通过分析大规模风力发电功率特性和风电预测时间序列特性，提出以深度循环神经网络进行预测，结合小波系数多尺度分析的隐马尔可夫预测方法，将深度学习引入到循环神经网络中来，构建基于多尺度隐马尔可夫模型-深度循环神经网络模型的大规模风力发电功率预测模型(MHMM-DRNN)，并通过仿真实验对多种预测方法进行分析比较。

2 风电预测时间序列特性

时序是一组按时间排序的序列变量，如流量、推力、气候、温度、湿度、压力等。时间序列的序列可以是基本时间，也可采用年等单位，没有具体规定。时间序列有确定时间特性和非确定时间特性。确定时间特性是指统计数据与时间发生联系的序列特征；非确定时间特性是指统计数据不与时间发生联系的序列特征。根据实际风电特性如装机容量特性、地域特性、气象特性等，结合时域分析与频域分析，研究对风力发电信号时间序列特性，探索风电预测时间序列分析和预测方法，以实现准确预测。预测风能主要通过分析风的历史时间序列，并对其进行统计预测风力发电功率提供指导，同时采用时变解释模型变量预判和评价风力发电功率[6-8]。

主要结果如下：

(1)连续预测法是风电预测中一种相对简单的方法。基于时间序列分析的预测模型，预测模型分析了风速的时间序列，然后将风速转化为风力发电功率。

(2)数值天气预报以电场周围的实际情况为基础，在一定的受限条件下，通过热力学和水动力学的数学模型解释天气演化过程的变化规律。因此，数值预测模型的输出(包括风、气温、气压等)在给定时间中详细预测了大气状态。

(3)物理预测方法利用微气象学理论，转换风电场功率曲线，可以描述风电场周围影响因素的特点和风电场设备的特点。

(4)采用统计方法无需考虑风电场周围影响因素的特征与风电设备特性的关系。

(5)如果只使用功率曲线进行预测，非线性风向曲线误差引起的误差将进一步放大，风速的微小变化可能导致较大的偏差功率，使用功率曲线的组合e测得的风速和功率曲线可使预测的根均方误差(RMSE) 增加近20%[9-12]。

3 风力发电功率预测模型

3.1 深度循环神经网络

循环神经网络(Recurrent Neural Network，RNN)是其特征为一个具有无限层次结构的深度神经网络。循环神经网络每个层次结构的基本属性是记忆数据，而不是联合处理相关数据。通过每次层次结构的推进，新数据被记忆到每一层次结构, 利用大量数据更新层次结构信息，循环神经网络可以得到大量数据信息[8-10]。深度循环神经网络作为一种深层神经网络，具备多层感应功能，其基本功能是时间反馈和信息传递。每次层次结构更新数据，新数据都通过层次结构之间联系进行传递，神经网络的每一层次结构可获取大量实时信息[12-14]。

设定n维导入序列x1，x2，…，xn，m维网络的隐层时间序列为h1，h2，…，hm，k维导出序列为y1，y2，…，yk，迭代公式如下：

ti=Whxxi+Whhhi-1+bh,hi=e(ti)

Si=Wyhhi+by,yi=g(si)

(1)

式中：Whx、Whh、Wyh为权值矩阵；bh、by为基底；ti为隐层参数导入，Si为导出序列的设置，他们同为k维的参数e、g提前设置的非线性向量参数函数：

(2)

其中第一层隐层的公式如下：

h(1)(xt)=σ(W(1)xt+b(1)+Uh(1)(xt-i))

(3)

式中：RNN模型基于状态参数的输入数据xt和状态参数对xt-1重构参数；h(1)(xt-1) 为计算网络结构h(1)(xt) 激活参数；W(1)和U为连接参数权值；b(1)是当前层的基底数据；σ代表sigmoid函数激活式为：

σ(z)=1/(1+e-z)

(4)

深度循环神经网络(Deep Recurrent Neural Network，DRNN)模型是基于多层RNN模型进行构建，数据具有良好的非线性化适用性，可以兼容不同的状态变量的变化。在此，通过式(5)来描述DRNN网络模型为：

h(i)(xt)=σ(W(i)h(i-1)xt+b(i))

(5)

式中：h(i)(xt) 描述第i层的状态变量，在此i大于1，同时对于每个隐层状态变量都有设置一定权重W(i)和基准值b(i)。

3.2 多尺度隐马尔可夫模型

在有限状态马尔可夫模型中，定义初始分布参数和状态转换概率矩阵参数来分析与评价当前状态的概率特征，而在隐藏的马尔可夫模型，只能分析与评价状态的过程概率。隐马尔可夫树模型更具体反映小波变换的聚合和持久性[15-16]。隐马尔可夫模型树结构的父节点和子节点之间的联系，可以类似于小波变换比例之间的依赖性特征。隐马尔可夫模型和小波变换之间的状态变量联系可以体现在隐马尔可夫树模型结构中，即当每个父状态参数通过一定概率变化到其他子状态参数，或者变化到子状态参数变量时，小波系数可以描述为高斯混合模型特征。相应的隐藏马尔可夫结构描述为：

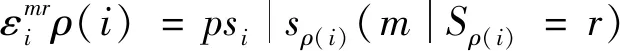
(6)

式中：ps1(m)为根节点Si的概率密度函数；给定父状态|Sρ(i)为r，子状态Si为m的条件概率。

参数向量θ表示为：

r=1,2,…,M}

(7)

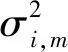
(1)初始化多尺度隐马尔可夫模型向量θ0；

(2)将迭代步长l定义为零；

(3)计算隐状态变量S的联合概率密度函数分布p(S|w,θl)；

(4)令θl+1为当Es[lnf(w,S|w,θl]最大时θ的参数值；

(5)l=l+1 ，如果θ的参数值达到收敛范围，则停止，否则转到步骤(3)。

3.3 MHMM-DRNN预测模型构建

多尺度隐藏马尔可夫模型用于大规模风电时间序列的预处理、多尺度分解和单分支重建，建立基于多尺度隐藏马尔可夫链的深循环神经网络的大型风力发电时间序列预测模型(为MHMM-DRNN模型)。图1显示了MHMM-DRNN预测模型的结构。

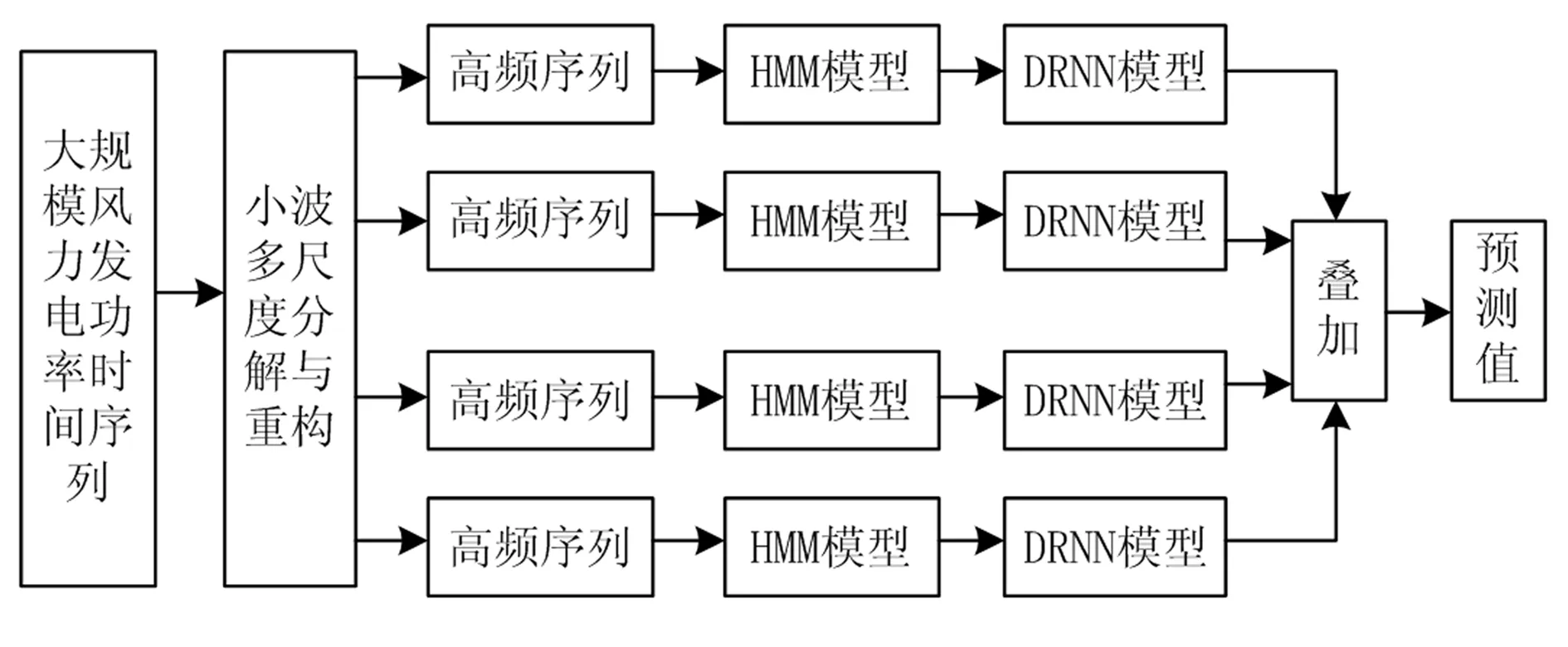
图1 MHMM-DRNN 预测模型结构

首先，将大规模风力发电功率时间序列数据进行多尺度隐马尔可夫分解和单支重构成多条序列。

MHMM-DRNN模型包括：

(1)数据准备：规范化数据，并保存其最大值和最小值；

(2)多尺度隐蔽马尔科夫分解和单分支重建；

(3)阶段空间重建；

对于时间序列{sk}，k= 1，2，…，m，采用先对{sk}进行相空间重构，通过转化为一个nin×mre的矩阵，矩阵结构如下：

式中：X为矩阵导入格式；Y为矩阵出格式。nin×mre的矩阵为n维时间序列x(t)，目标序列可以设置为y(t)。

(4)对DRNN模型进行训练；

(5)经过训练的DRNN模型对子系列的测试样本预测；

(6)多组训练数据分别对DRNN模型进行训练；

(7)用训练好的DRNN模型对子序列的测试样本进行预测。

4 实例

选取内蒙古某风电场2015年历史数据作为研究对象，利用MHMM-DRNN预测模型进行功率预测。数据为采集单台风机轮毂处功率。以二期工程2015年数据为例，选取现有的2015年数据进行分析。由于二期工程2014年底才投运，因此前几个月的数据采集情况稳定性不佳，故选取2015年2月至7月数据作为历史实测数据，如图2所示。

图2 2015年2月至7月数据作为历史实测数据

考虑到随机性使风速可能超过设定范围，2015年2月开始至7月的设备故障、电路故障、风机故障、维护检修、设备更换等原因造成的数据不完整现象(例如2015年5月中一段时间数据缺失)可以使用期平均数据进行代替。如2015年2月开始至7月风速波动不大，比较稳定，因此用平均值代替对预测的准确性以及整体评价影响较小。

单台风机2015年6月6日MHMM-DRNN预测模型功率预测数据如表1所示，其中相对误差均值约为25.12%，均方根误差为14.45。

表1 单台风机2015年6月6日功率预测数据

通过对风电场功率数据进行分析，选择将负功率数据剔除，使用期平均数据代替缺失值后，得到如表1的风电场风机功率预测数据。除了风电功率本身的随机性以及波动性之外，由于风电场建设运行刚刚开始，设备兼容性有待调整，因此风电场风机功率提取受到了较大的影响。

根据图3所示，各种单一模型相对误差平均值：BP神经网络约为31.56%，ARMA模型约为23.20%，小波分析约为26.11%，而MHMM-DRNN预测模型为16.85%。由此可见，MHMM-DRNN预测模型比BP神经网络和小波分析预测值更准确，更接近真实值。

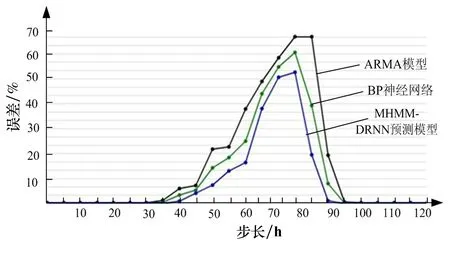
图3 单台风机功率不同方法误差分析

5 结论

通过分析大规模风力发电功率特性和风电预测时间序列特性，结合小波系数多尺度分析的隐马尔可夫预测方法，通过将深度学习引入到循环神经网络，构建基于多尺度隐马尔可夫模型-深度循环神经网络模型进行风电功率预测。通过仿真实验分析可知，本文提出的方法有效提升了大规模风力发电功率预测精度。