田坪特大桥桩基础混凝土力学特性的数值模拟研究

张 雷

(中铁十九局集团第三工程有限公司，辽宁 沈阳 110136)

0 引言

随着国家经济的飞速发展，基础设施建设也在快速推进。桥梁作为交通基础设施中的重要组成部分，其桩基础的承载能力是桥梁安全稳定运营的关键。特征强度是划分混凝土及岩石类材料破坏阶段的临界参数，不同加载速率下混凝土的特征强度将会发生改变，因此有必要对加载机制下混凝土特征强度进行研究。

近年来，颗粒离散元法(PFC，Particle Flow Code)逐渐成为混凝土及岩石类材料力学特性研究的主流方法。该方法最初是基于球状颗粒(3D)和圆形颗粒(2D)模型而逐渐发展起来的，适用于细观颗粒可由球状颗粒近似代替、且颗粒数目相对较多的材料。目前，该方法在岩石类材料数值试验方面应用较多。石崇等[1]系统阐述了颗粒流数值模拟技术及应用。田丰等[2]基于PFC3D对某水电工程混凝土进行了数值模拟研究，并建立冻融损伤本构模型，分析了冻融损伤后混凝土内部的裂隙扩展规律。王俊等[3]利用颗粒流软件对碳化混凝土的细观裂纹扩展机制进行了研究，通过声发射技术记录了混凝土破裂过程中产生的声发射信号，对比细观裂纹和声发射信号可知二者分布情况相似，表明颗粒流软件可在一定程度上对混凝土进行研究。李博等[4]通过PFC数值模拟软件建立了水下导管法混凝土模型，并基于颗粒流理论和细观理论建立混凝土宏细观力学特性之间的关系。刘东海等[5]基于支持向量机模型和自适应差分法给出了沥青混凝土心墙颗粒流模型的参数反演方法。李守巨等[6]为研究混凝土细观参数取值问题，建立了混凝土材料的巴西劈裂试件的二维颗粒流程序计算模型，提出了一种细观参数的估计方法。

综上可知，已有成果对于不同加载速率下桥梁桩基混凝土的力学响应机制研究较少，本文在颗粒流数值模拟软件PFC2D的基础上，对不同加载速率下桩基混凝土的力学响应机制进行研究，分析不同加载速率下混凝土的宏观强度特性，为类似工程提供参考。

1 数值模型建立与细观参数标定

1.1 数值模型建立

本文利用二维颗粒离散元软件PFC2D对田坪特大桥桩基混凝土特征强度的加载速率效应进行数值模拟研究，颗粒间接触采用平行黏结模型，加载方式采用位移控制加载，具体试验步骤如下：

(1)首先建立满足混凝土力学试验标准的试样，PFC2D中模型厚度通常取单位厚度，因此双轴压缩试样尺寸为长50 mm，高100 mm(图1)，图中灰色颗粒代表细骨料，青蓝色颗粒代表粗骨料。

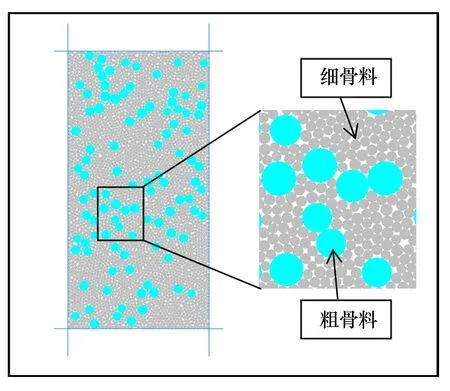
图1 桩基混凝土数值试验模型

(2)然后对试样施加侧向应力，即上下左右墙体同时以相同的加载速率对试样施加侧向应力至预定值，待侧向应力稳定后，以某一固定加载速率对试样施加轴向荷载直至失稳破坏。

(3)试验结束后，在视图窗口上直接导出试验数据，包括应力-应变曲线、试样位移云图等。

本文为研究不同加载速率对桩基混凝土力学特性的影响，结合室内物理试验、工程实际情况和PFC数值模拟软件的特点，拟设置加载速率分别为0.5、1.0、1.5、2.0和2.5 mm/s，设置侧向应力为5 MPa，进而对不同加载速率下混凝土的力学响应机制进行分析。

1.2 细观参数标定

采用颗粒离散元法对混凝土材料进行数值模拟时，细观参数的选取是否符合实际材料内部颗粒之间的接触特性是数值试验的关键。目前的数值试验细观参数标定通常都是由宏观试验开始，从宏细观变量之间对应关系的角度出发，通过"试错法"来反演细观参数。

本文对田坪特大桥桩基础混凝土的力学性质进行数值模拟研究时，同样采用"试错法"对数值试样进行细观参数标定。首先对试样进行单轴压缩试验，获取混凝土的单轴压缩应力-应变曲线，然后通过调整相关的细观参数使数值试样的宏观力学行为能够表现出混凝土真实的力学行为，当数值试验曲线与室内试验曲线基本接近时，即认为该组细观参数可基本满足混凝土的宏观力学特性，并在后续数值试验中继续使用。表1为满足本文混凝土试样的细观参数。

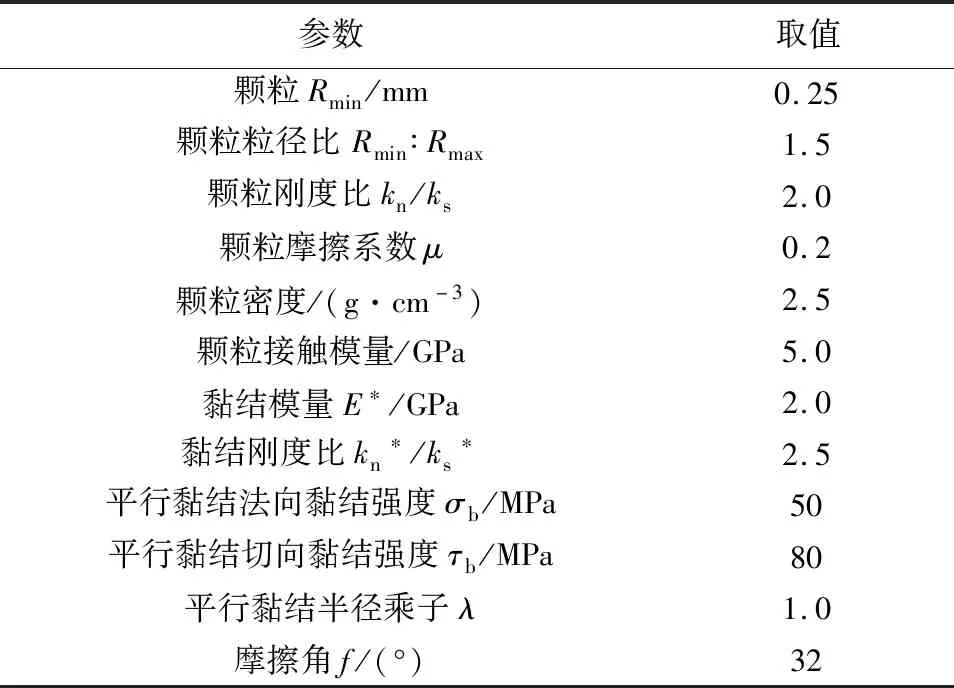
表1 混凝土试样的细观参数

本文室内试验采用MTS815.02多功能伺服试验机，室内试验和数值模拟试验结果如图2所示。从图2中可以看出，室内试验曲线与数值试验曲线的变化规律大体相同，其中室内试验曲线的峰值强度略高于数值模拟曲线，二者峰值应变较为接近，峰后曲线均表现出脆性破坏特征。二者不同点在于数值模拟曲线无明显压密阶段，产生原因是模型生成时已完成自平衡，内部孔隙已被压密，致使数值模拟曲线直接从弹性阶段开始。除压密阶段外，二者在其他各阶段均表现出显著的相似性，因此采用PFC数值模拟方法可较好地反映混凝土的宏观力学性质，且PFC操作简单，能够确保试样的一致性，还可有效节约室内试验成本和时间。

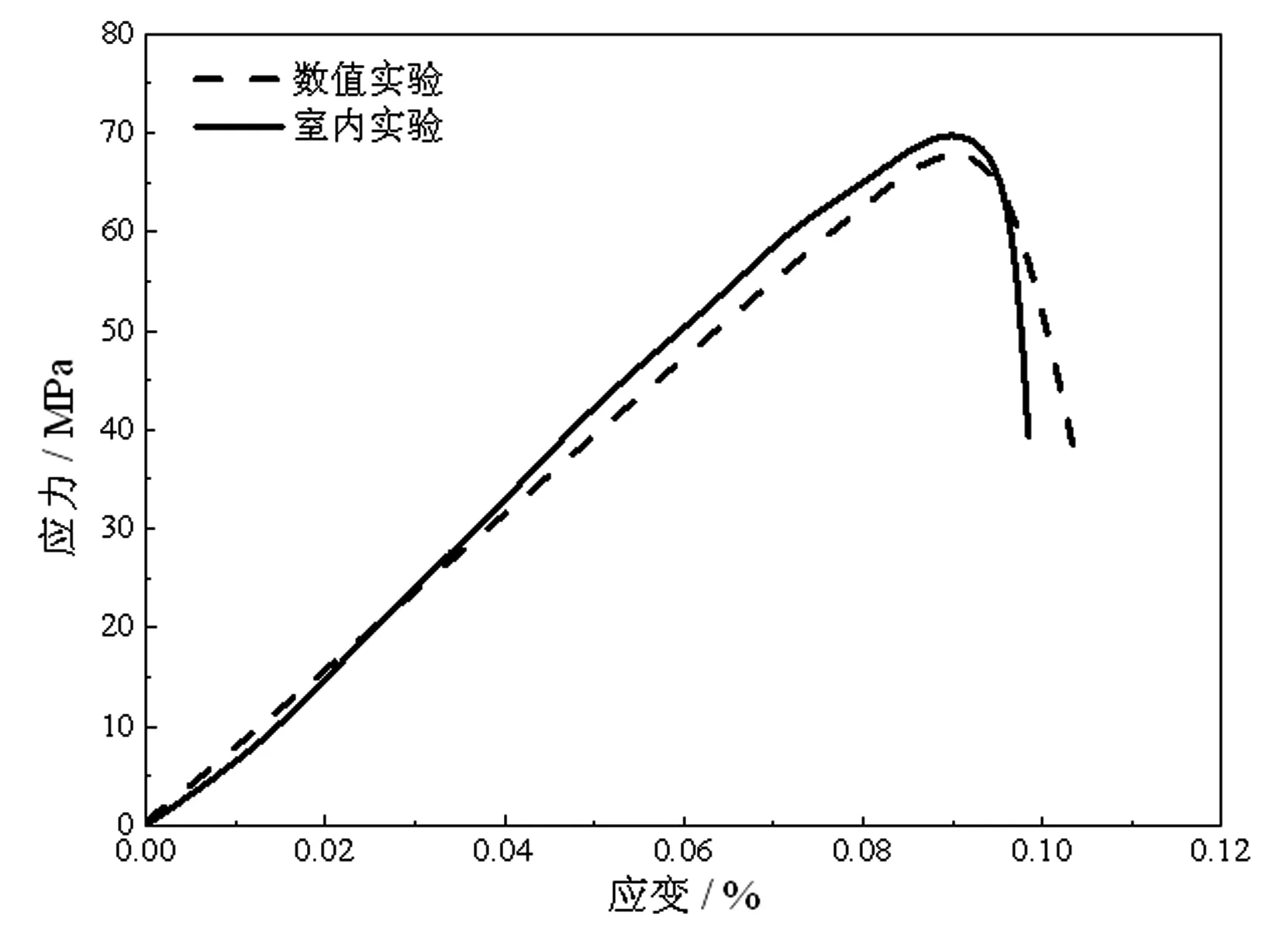
图2 数值试验与室内试验对比曲线

2 数值模拟结果分析

2.1 应力-应变曲线分析

图3为侧向应力5 MPa不同加载速率下桩基混凝土数值试验全过程应力-应变曲线。由图3可知，不同加载速率下混凝土数值试验曲线的变化趋势基本一致。应力-应变曲线全过程大体可分为五个：弹性阶段、裂隙稳定扩展阶段、裂隙不稳定扩展阶段、峰后阶段和残余阶段。

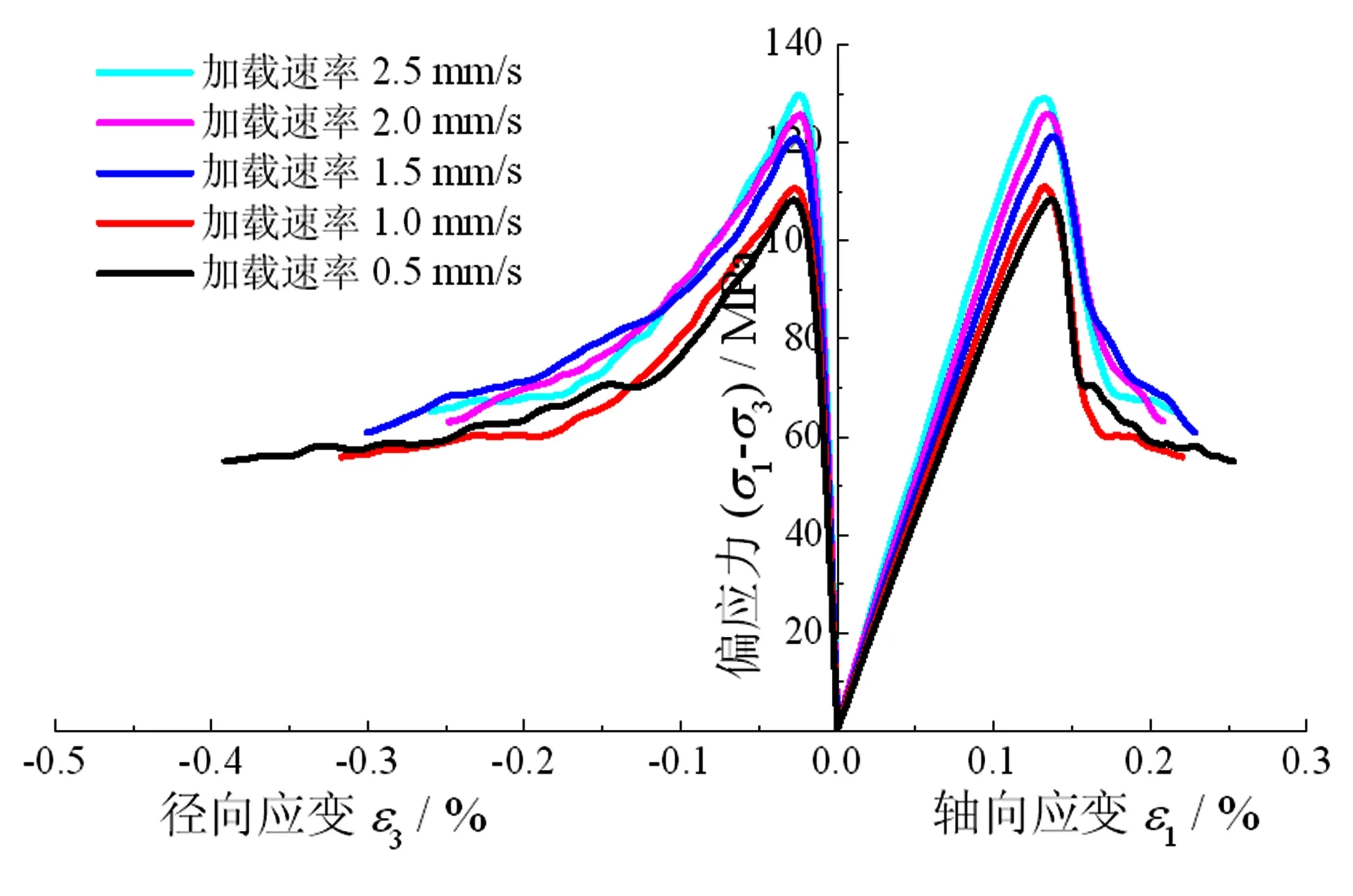
图3 不同加载速率下混凝土应力-应变曲线

表2为不同加载速率下混凝土的数值试验力学参数计算结果。从表2中可以看出，试样的峰值强度、弹性模量均随加载速率逐渐增大，而泊松比则随加载速率呈逐渐递减变化。当加载速率为0.5 mm/s时，试样的峰值强度为108.57 MPa，弹性模量为8.77 GPa，泊松比为0.227；随着加载速率的逐渐增大，当加载速率分别为1.0、1.5、2.0和2.5 mm/s时，试样的峰值强度相对0.5 mm/s时分别提升了2.81%、11.83%、16.28和21.96%，弹性模量分别提升了2.05%、3.99%、5.02%和7.53%，泊松比分别减少了0.88%、2.20%、3.08%和4.41%，可见，加载速率对混凝土的峰值强度影响显著。为了更加直观地看出各力学参数的加载速率效应，将表2中数据绘于图4。

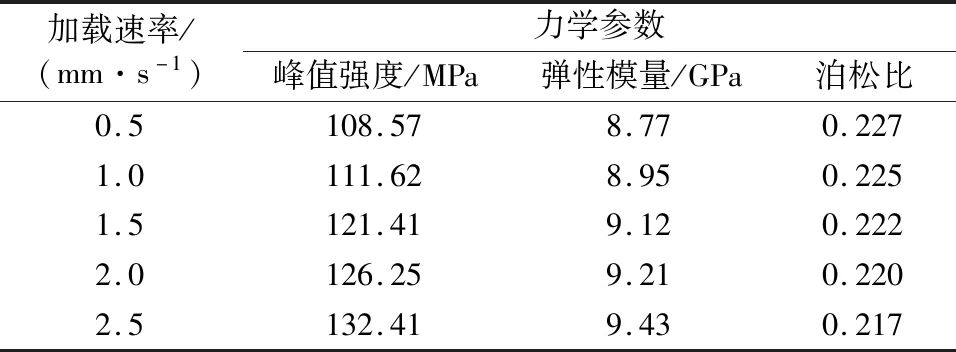
表2 不同加载速率下混凝土的力学参数结果

图4 混凝土的力学参数与加载速率之间关系

2.2 特征应力分析

混凝土的破坏过程与岩石的破坏过程较为相似，大致分为微裂隙压密阶段、弹性变形阶段、塑性屈服阶段及峰后残余阶段，其中塑性屈服阶段包括裂纹稳定扩展阶段和裂纹不稳定扩展阶段。σci、σcd分别表示混凝土由弹性变形阶段进入塑性屈服阶段的起裂应力和由裂隙稳定发展阶段进入裂纹不稳定发展阶段的扩容应力。本文采用裂隙体积应变法来计算不同加载速率条件下的起裂应力σci和扩容应力σcd，以此来分析数值混凝土试样的起裂水平与扩容水平的变化情况。根据岩石力学的计算方法，体积应变可表示为：

εv=ε1+2ε3

(1)

式中：εv为体积应变；ε1为轴向应变；ε3为径向应变。

裂隙体积应变表达式为：

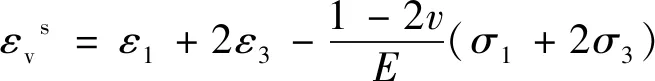
(2)

式中：εvs为裂隙体积应变；E为弹性模量，GPa；v泊松比；ε3为径向应变；σ1和σ3分别为轴向应力和围压，MPa。

式(2)中各参数均可由数值试验得到，根据式(2)对不同加载速率下数值混凝土试样的裂隙体应变εvs进行计算，并绘制裂隙体应变εvs、体积应变εv随轴向应变ε1的分布曲线。限于篇幅，文中仅列出了加载速率为1.5 mm/s时的体积应变与裂隙体积应变曲线，见图5。图5中起裂应力对应的轴向应变是裂隙体积应变由零到非零的临界点，扩容应力对应的轴向应变是体积应变的最大值点。

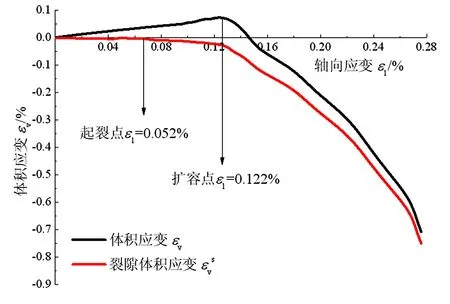
图5 加载速率为1.5 mm/s时混凝土体积应变与轴向应变之间关系

根据试验结果，不同加载速率下混凝土试样的体积应变、裂隙体积应变随轴向应变的分布规律大体相同，由于数值试验应力-应变曲线并未表现出明显的压密阶段，因此图5中的裂隙体积应变同样未表现出明显的压密过程。裂隙体积应变在轴向应力达到起裂应力前恒为零，当轴向应力处于起裂应力与扩容应力之间时，试样内部裂隙以稳定速率扩展，裂隙体积应变稳定增长。当轴向应力达到扩容应力时，体积应变达到拐点值，此后试样进入裂隙不稳定扩展阶段，试样内部裂隙开始快速发育，裂隙体积应变同样快速增大。

根据图5中的起裂点、扩容点所对应的轴向应变值和图2应力-应变曲线，即可得到相应的起裂应力和扩容应力。表3为不同加载速率下混凝土试样的起裂应力和扩容应力，表中起裂水平为起裂应力与峰值强度的比值，扩容水平为扩容应力与峰值强度的比值。图6为表3的直观反映。

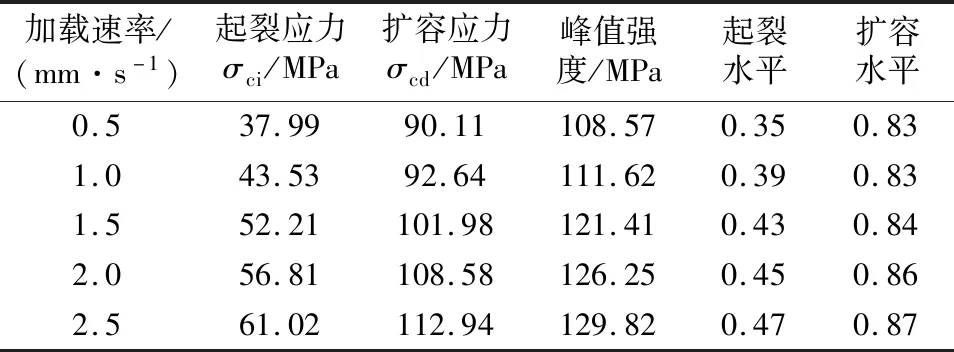
表3 不同加载速率下混凝土试样的特征应力指标

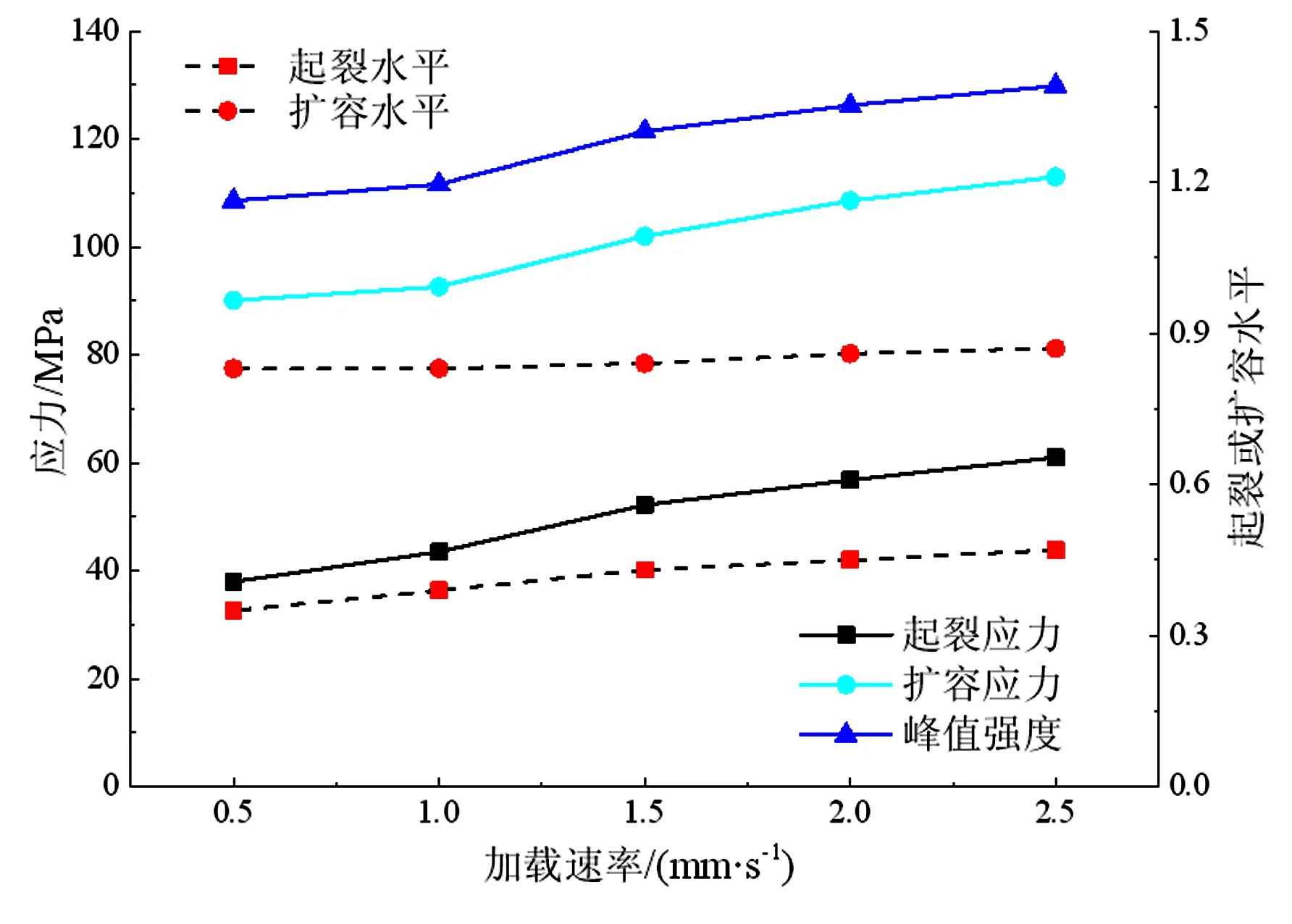
图6 混凝土试样的特征应力指标与加载速率之间关系

由表3和图6可以看出，加载速率对混凝土的起裂和扩容作用具有显著影响，试样的起裂水平与扩容水平均随着加载速率的增大呈逐渐递增趋势，但增幅逐渐减小。当加载速率为0.5 mm/s时，数值混凝土试样的起裂水平为0.35、扩容水平为0.83，当加载速率分别为1.0、1.5、2.0、2.5 mm/s时，试样的起裂水平分别为加载速率0.5 mm/s时的1.11、1.23、1.29和1.34倍，扩容水平分别为加载速率0.5 mm/s时的1.0、1.01、1.04和1.05倍，加载速率由0.5 mm/s提升至2.5 mm/s，试样的起裂水平提升了34.28%，扩容水平提升了4.82%，可见加载速率对混凝土内部裂隙的扩展具有促进作用，且加载速率对混凝土起裂水平的影响更为明显。产生起裂和扩容水平提升的原因是加载速率的增大使混凝土试样内部完整部分产生应力滞后，含原始微裂隙分布在受力后快速扩展。加载速率越大，试样内部完整部分产生应力滞后效应越明显，原始裂隙扩展速度越快，因此混凝土试样的起裂水平随加载速率逐渐提高。但结合室内物理试验和工程实际问题，加载速率不可能无限制地增大，应在某一范围内取值，本文结论适用加载速率为0.5～2.5 mm/s范围内。

5 结论

(1)通过细观参数标定，找到了满足本文桥梁桩基混凝土宏观力学特性的数值模拟微观力学参数，对比室内试验和数值模拟曲线发现，除压密阶段外，二者在其余阶段均表现出显著的相似性，数值模拟曲线无压密阶段，原因是模型生成时已完成自平衡，内部孔隙已被压密，致使数值模拟曲线直接从弹性阶段开始。

(2)随着加载速率的逐渐增大，混凝土试样的峰值强度、弹性模量均呈逐渐递增趋势，泊松比随加载速率逐渐递减；加载速率由0.5 mm/s增大至2.5 mm/s，峰值强度增长了21.96%，弹性模量增长了7.53%，泊松比减少了4.61% ，可见加载速率对混凝土的峰值强度影响更为显著。

(3)随着加载速率的逐渐增大，混凝土试样的起裂应力和扩容应力均呈逐渐递增趋势，起裂水平和扩容水平同样逐渐递增，但二者变化幅度较小。加载速率由0.5 mm/s增大至2.5 mm/s，试样的起裂水平提升了34.28%，扩容水平提升了4.82%，可见加载速率对混凝土起裂水平的影响更为明显。