一种基于QR 分解的观测矩阵优化方法*

周琦宾 ，吴 静 ，2，余 波

(1.西南科技大学 信息工程学院，四川 绵阳 621000；2.西南科技大学 特殊环境机器人技术四川省重点实验室，四川 绵阳 621000)

0 引言

压缩感知理论(Compressed Sensing，CS)是一种有别于传统Shannon-Nyquist 采样定理的信号欠采样理论。该理论指出，对于稀疏或可压缩信号，可以通过线性投影的方式将大部分信号的信息投射在低维空间，然后利用非线性解码的算法将信号恢复到原始状态。

CS 方法被广泛应用于无线通信、模式识别和雷达成像等领域。观测矩阵的设计是CS 方法的关键研究内容之一，构造性能良好的观测矩阵对于信号的压缩观测以及重构都起到了至关重要的作用[1]。现有的文献对观测矩阵的约束条件展开了一系列的探究，文献[2]中阐述了限制性等距原则(Restricted Isometry Property，RIP)；文献[3]提出利用零空间性质作为观测矩阵的约束条件，但由于观测矩阵是否具备约束条件难以准确判断，往往需要涉及组合复杂度的相关问题，因此该方法的实际应用具有一定难度。

文献[4]中为有效测量观测矩阵性能，将矩阵和稀疏基间的互相关性当做衡量标准，相关性越低，信号适应的稀疏度范围越大，精确重建信号所需观测值的数目越少；文献[5]主要以Gram 矩阵为基础伪逆求解观测矩阵，该研究采用了阈值函数，其中的收缩因子能够根据需要进行调节，但是这种方法比较耗时，在收缩过程中可能会产生绝对值较大的相关系数；文献[6]中ABOLGHASEMI V 首次提出利用梯度下降法使得Gram 矩阵逼近单位阵，但是该算法收敛速度较慢并且可能陷入局部最优；文献[7]提出使用矩阵特征值分解对观测矩阵进行优化，将特征值分解后的Gram 矩阵的特征值取平均值，然后间接优化Gram 矩阵的非对角线元素，该方法在一定程度上能够降低矩阵的整体互相干性，但是在使用某些恢复算法(如SP 算法)的情况下，可能无法重建原始信号，在适用范围上有一定的局限性。

文献[8]的研究表明，重构算法要想准确地实现恢复信号的目的，必须满足的条件是使观测矩阵列向量具备一定的线性独立性，而且越强的独立性能够保证重建信号具有越高的质量。

通过梳理相关研究理论，本研究借助于QR 分解的方式提高观测矩阵列向量的独立性，并将QR 分解与自适应梯度下降观测矩阵优化算法相结合，提出了一种Gram 矩阵优化算法，并在实验上对该方法的可行性进行验证。

1 压缩感知理论框架

由CS 理论，信号y 能够稀疏表示为：

其中，α∈RM×1为稀疏信号；Ψ∈RM×L为稀疏基；Φ∈RM×N为投影矩阵；y∈RM×1为观测信号。同时D=ΦΨ 为观测矩阵，需要满足限制性等距原则。由于M＜＜N，可以同时实现信号压缩和采样，大大减少了采样量，从而降低了数据的传输压力。

把压缩感测理论应用于实践操作，需要从观测到的信号y 重建原始信号，这被称为信号重建过程，其原始模型为：

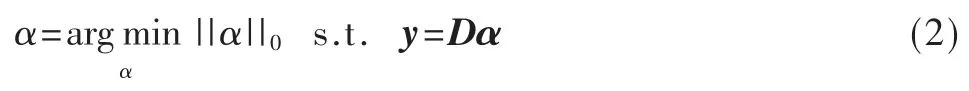
然而，对l0范数问题的求解是NP-hard 的，运算量十分巨大，因此无法在实践中使用。有研究表明，在一定的条件下，可以使用l1范数解代替l0范数解，这两个解等价[8]，如式(3)所示：

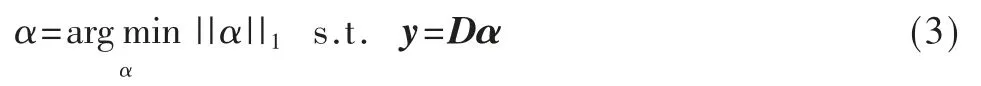
式(3)是一个凸优化问题，要想获得最优解，可以采用基追踪(BP)算法进行求解。

2 优化算法

目前，现有的观测矩阵几乎都存在一些不足，如随机观测矩阵的不确定性与硬件难以实现性；确定性观测矩阵虽然更易于设计快速算法，但使用其采样时重建信号的质量却差强人意。寻求需要更少观测值且具有较好稳定性的观测矩阵是观测矩阵的研究重点。

为得到更好的重建效果，本文提出了一种基于QR分解与自适应梯度下降法相结合的优化方法，以满足观测矩阵与稀疏基础之间的相关性以及观测矩阵列向量间的独立性要求。

2.1 矩阵列向量的独立性与QR 分解

文献[9]研究表明：观测矩阵的优化可以通过增加矩阵的最小奇异值来实现，原因在于最小奇异值和列向量具有显著的线性关系，要想增强矩阵列向量的独立性，就要使其最小奇异值较大，此种方法不会改变原矩阵的性质。

QR 分解不仅可以增大矩阵的最小奇异值，而且可以保持该矩阵的其他性质不变[10]。具体的操作步骤是通过分解矩阵A∈RM×N获得正交矩阵Q∈RM×N(QTQ=I)和上三角矩阵R 的积，也就是A=QR。对R 进行分析，能够看出其对角线元素比非对角线元素大得多，利用这一发现，将R 的非对角元素设置为零得到（，得到A 的还原矩阵：

1）人力支持。专业实验室的运行需要人力资源作为基础，实验室管理人员作为其看护者，必须兢兢业业，保证实验室安全。专业实验室内一般存放大量化学试剂和物理仪器，尤其是很多化学试剂具有一定的危险性，即专业实验室本身就是较易发生安全事故的场所。在专业实验室开放的情况下，学生由于经验不足及容易大意，易发生损坏实验室仪器及安全问题等事故，一旦发生，后果严重。这就对专业实验室管理人员提出更高的要求，不仅要严格要求自己，细致管理仪器试剂，也要严格要求学生。同时，指导教师也应充分发挥作用，认真指导学生操作，避免错误发生。

2.2 基于自适应梯度下降法降低相关性

观测矩阵设计的目的是压缩和采样信号，并确保可以从观测值中准确恢复原始信号。设观测矩阵Φ、稀疏基Ψ，对矩阵D=ΦΨ 进行列单位化处理，得到，文献[4]的研究表明，观测矩阵的性能可以通过观测矩阵与稀疏基之间的相关数来评估，并给出了观测矩阵与稀疏基之间的相关系数定义：

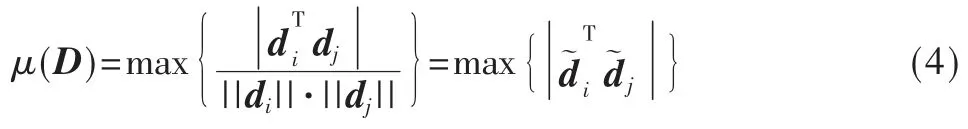
式中，di与(i=1，2，…，N)分别表示矩阵D 与的列向量。设，则称G 为Gram 矩阵。

现有理论表明，相关系数μ(D)越小，被观测信号中包含的信息就越多[5]。互相关数的最佳情况是零，但无法达到该值。它有一个下限μE，即Welch 界:

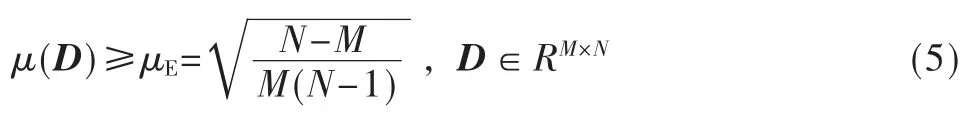
由式(5)知，Welch 界的大小与N 和M 的长度有关。当观测信号长度M 和原始信号长度N 满足式(6)的条件时，互相关系数能够达到Welch 界[11]。

等角紧框架(ETF)是一种特殊的Gram 矩阵[12]，其对角线元素的值均是1，非对角线元素为μE。所以要想将观测矩阵和稀疏矩阵的互相关性尽可能地接近等角紧框架，要得到对Gram 矩阵进行优化后的矩阵Gopt，需要求解式(7)。

用梯度下降法求解Dopt，同时完成D 的更新[13]，计算方法如式(10)所示：

其中，梯度用▽f(D)表示，步长用λ 表示。共轭梯度的带入能够有效减少迭代次数，同时对每次梯度下降的方向进行更新能够加快收敛的速度，这称为自适应梯度下降算法[14]。

2.3 观测矩阵优化

观测矩阵优化算法的初始化涉及的变量包括：稀疏基Ψ，随机高斯矩阵Φ，观测矩阵D=ΦΨ，阈值μG，迭代次数K1、K2，搜索步长λ，约束系数β，l=0。

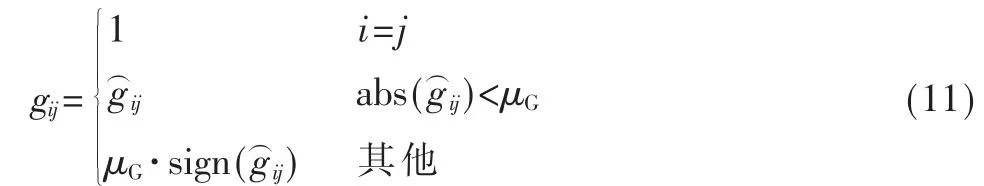
(2)由式(10)计算初始下降方向d0=-▽f(D)，初始化L=0；更新DL+1=DL+λ·dL；更新下一次下降方向dL+1=-▽fL+1+β·dL；更新dL=dL+1，DL=DL+1；

(3)L=L+1，若L=K2，则执行步骤(4)，否则继续更新DL+1=DL+λ·dL；

(4)l=l+1，如果l=K1，则计算：Ψ-1，否则执行步骤(1)；

(7)输出观测矩阵Φ。

3 实验与分析

分别采用QR 分解算法、文献[5]中Abolghasemi 优化算法与本文提出的优化算法进行进行对比试验，以验证本研究中所设计的算法的性能。测试环境：MATLAB R2016a，英特尔i5-4210U，内存为4 GB。

3.1 一维信号采样与重建

首先，使用随机排列(Randperm)的方法生成25 组长度n=200 的一维稀疏信号，其中，初始投影矩阵为高斯随机矩阵，稀疏字典为DCT 变换矩阵，重构算法为OMP算法。

图1 不同观测值下各算法重建信号的性能比较

图1 给出了在相同稀疏度下(K=4)，原始高斯矩阵、QR 分解算法、Abolghasemi 优化算法和本文提出的优化算法对稀疏信号重建质量的影响。图1(a)显示了不同优化算法对稀疏信号重建的峰值信噪比(PSNR)，能够看出基于不同算法的稀疏信号重建的峰值信噪比随着观测值的增加而增加。在观测值M 个数较高情况下，未优化的原始高斯矩阵峰值信噪比最低，本文优化算法重建稀疏信号的峰值信噪比相对QR 分解与Abolghasemi 优化算法分别提高了1.9 dB 和1.4 dB。根据图1(b)和图1(c)中展示的情况可以看出：将稀疏度和信号长度控制在固定水平，基于不同算法的稀疏信号重建的误差以及错误个数会随着观测值的增加而降低，本文所采用的优化算法是4 种算法中误差及错误个数最低的一种。

针对不同观测矩阵优化算法对信号稀疏度的适应性进行研究，分别确定观测值M=30、稀疏度M∈[2，8]，在此基础上得出的基于4 种算法重建信号的质量随稀疏度变化曲线如图2 所示。

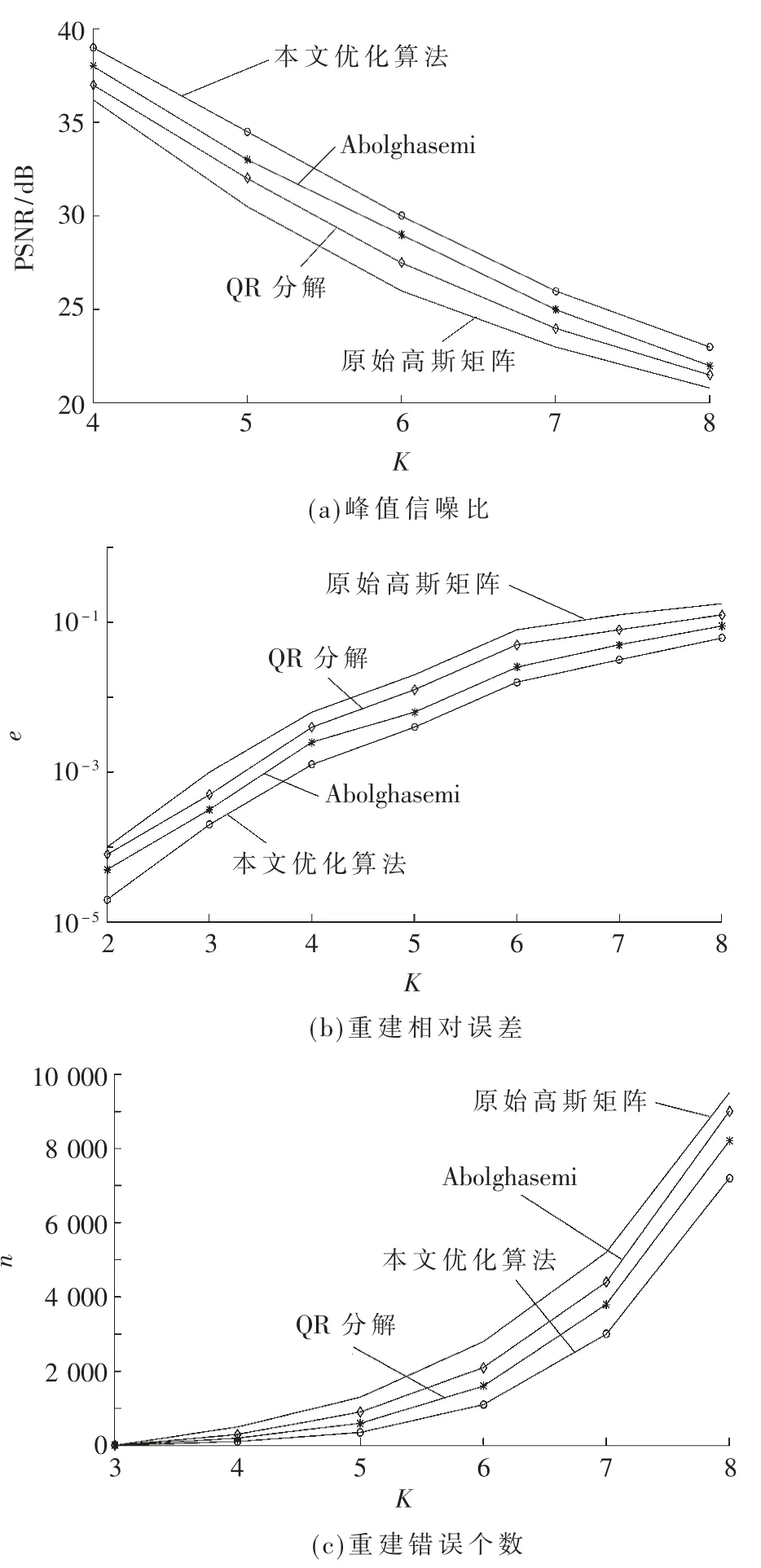
图2 不同稀疏度下各算法重建信号的性能比较

由图2 可以看出，当信号长度和观测值个数M 固定时，随着稀疏度的增加，相对峰值信噪比、重建误差以及重建错误个数都在变差，表明稀疏度越差，重建难度越大，重建精度越低。从图2(a)可知，在稀疏度K=5 情况下，相较于QR 分解算法、Abolghasemi 优化算法，本文采用的观测矩阵优化算法重建信号的峰值信噪比平均提高了1.5 dB。

3.2 二维图像采样与重建

在本节中，对二维图像的压缩感知采样和重建效果进行测试。采用分辨率为256×256 的标准灰度图像CameraMan 用作测试对象。首先把灰度图像归一化后，将其转换为65 536×1 的列向量，观测率为50%，即投影矩阵为32 768×32 768。与上一小节类似，分别采用未优化、QR 分解优化、Abolghasemi 算法优化和本文算法优化后的高斯矩阵进行采样，然后使用OMP 算法进行重建。实验结果如图3、表1 所示。

图3 不同算法优化观测矩阵后的重建图像

表1 优化前后重建参数比较

由图3 可以看出，在观测值的50%下，原始高斯矩阵、QR 分解优化算法、Abolghasemi 优化算法和本文优化算法都可以完整重建原图。然而，经过本文算法重建的图像部分噪点更少，整体细节方面更清晰，重建效果更好。表1 给出了重建图像的峰值信噪比与相对误差的比较，其中，相对误差re=||X-X′||F/||X||F，X 为原图像，X′为重建图像，||·||F为Frobenius 范数。从表1 的数值上可以看出，经过本文算法优化后的观测矩阵重建的图像峰值信噪比较高，相对误差最低。

4 结论

通过对已有的压缩感知观测矩阵算法进行优化，本文提出一种结合QR 分解与自适应梯度下降的观测矩阵优化算法，获得了性能较优的观测矩阵。该矩阵具有较高的列独立性，并且与稀疏基之间具有较低的互相关性。实验结果表明了该算法的有效性，并在重建质量方面有较大的优势。后期的研究工作将着力于进一步降低算法的复杂度，提高重建信号的效率。