基于蒙特卡洛方法的四杆机构输出角可靠性研究*

刘晓静

（山西工程职业学院，山西 太原 030009）

机械可靠性中机构可靠性是非常重要的一部分，它在工程实际中不可缺。现有国内外很多学者研究机构的可靠性。1966年H. P勃鲁也维奇等[1]深入研究了机构运动误差。史天录[2]首次明确归纳出了机构运动精度可靠性分析的基本原理。张义民[3]则提出了机械动态与渐变可靠性理论。四杆机构运动过程中，输出角可靠性会随着时间的变化而发生改变。因此，基于Monte Carol 进行四杆机构输出角可靠性研究，为后续进行可靠性灵敏度研究打好基础。

1 可靠性研究状况

可靠性是产品元件或系统机构在一定条件和一段时间内执行某种设定功能而不发生故障的概率。结构可靠性定量理论的研究始于美国Freuenthal于1947 年在 ASCE 期刊上发表的论文中首次提出了应力-强度干涉模型，从此可靠性理论与方法开始引起理论学术界和实际工程界的普遍关注与重视。

近年来，国内外很多学者对可靠性理论、可靠性的设计方法都进行了比较深入的研究。张义民利用神经网络方法和随机摄动技术对装备零部件的可靠性进行了优化设计和稳健设计。Rhyu以平面四杆机构杆长尺寸误差和运动副精度概率分析为基础进行了机构可靠性优化设计。史天录首次明确归纳出了机构运动精度可靠性分析的基本原理，并对间隙随机特性的研究做了完善[4]。

系统动态可靠性理论的研究最早可以追溯到20世纪40年代。Rice 首先提出了著名的首次超越概率公式，为首次超越破坏的动态可靠性理论奠定了基础。Crandall将数值模拟方法引入首次超越问题中，进一步发展了基于首次穿越模型的动态可靠性分析理论。

2 蒙特卡洛方法及可靠性

系统不能完成规定功能的概率表示为失效概率pf。系统的可靠度pr与失效概率满足以下关系式：

系统可靠性分析的主要问题就是处理系统的随机问题来确定系统的失效概率。

如果连续随机变量Z的概率密度函数为fz(z)，则由失效概率的意义可知：

如果用fX(x) =fX(x1,x2,…,xn)表示基本随机变量X= (X1,X2,…,Xn)T的联合概率密度函数，用表示联合累积分布函数，那么系统的失效概率可表示为：

若各基本随机变量Xi之间相互独立，且Xi的概率密度函数为，则失效概率为

可靠指标是可靠性指标的简称[5]。由于基本随机变量的不确定性，其联合概率密度函数的获取比价困难，联合概率密度函数的计算也非常困难，因此，在工程上一般不使用式（5）来计算失效概率。根据可靠性指标与失效概率的对应关系，通过计算可靠性指标来确定系统的可靠性。

正态分布Y～N (0，1)，那么其概率密度函数和累积分布函数为：

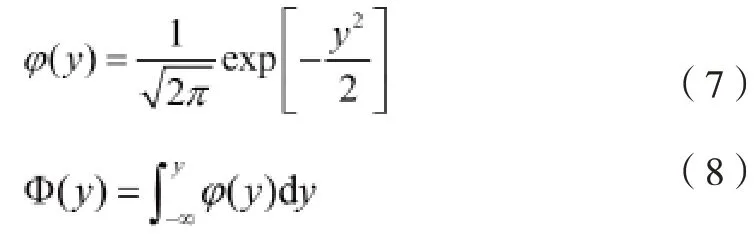
将式（6）代入式（4），并注意到式（7）和式（8），则失效概率[6]为

可靠性指标、失效概率和可靠概率就可以分别表示为：

上述对可靠指标的计算是建立在功能函数服从正态分布的条件下。当pf≥0.001（或β≥3.0902）时，失效概率的计算结果能够满足工程上所要求的精度，因此，可以不考虑基本变量的分布类型而简化计算过程；当失效概率或可靠指标不满足以上关系时，必须考虑功能函数的概率分布形式。

Monte Carol 首先需要根据随机变量的概率分布，产生足够多的样本，即随机数。不同分布的随机变量通过抽样得到不同的随机序列。最基本的随机变量是区间在（0，1）上的均匀分布。

随机数直接生成法是指根据概率分布的定义在该区间内抽取满足分布的随机数。

反变换法：连续的随机变量X 的累积分布函数为FX(x)，且FX(x)单调增加，u 为FX(x)的随机数，则X 的随机数为；对于离散的X，其概率分布为P（x=xi）=Pi（i=1，2，…），，用数值法找出最接近u 的（FX）xi，若满足u≤FX(xi)或FX(xi-1) ≤u≤FX(xi)时，xi为X 的一个随机数。

舍选法：按照一定的标准选择或者舍弃（0，1）上的均匀随机数，从而得到X的随机数x。

Monte Carol 是通过随机抽样的方法解决在极限状态方程未知的情况下的可靠性分析，最简单也是最直接的方法。Monte Carol 解决问题的步骤分为四步：1）定义极限状态方程；2）根据随机变量的联合概率密度分布产生随机数；3）将随机数代入极限状态方程中求解直到完成设定的抽样次数；4）计算结构的失效概率。

Monte Carlo模拟过程中，采用样本均值代替总体均值，数学期望可以用样本函数的均值来估计：

功能函数是结构响应量r（x）与机构响应阈值r*之差，即g（x）= r（x）- r*。失效域F为集合为{ x | g（x）＜b}所构成的区域，安全域为失效域的补集，即S={ x | g(x)≥b}。安全域和失效域之间存在一个分界面，将功能函数简记为g，即方程：

假定结构的功能函数为Z=gX(X)，随机变量X 的概率密度函数fX(X)。按fX(x)对X进行随机抽样，所得的样本代入功能函数Z=gX(X)，Z＜0 则记为失效一次。设模拟次数为N，其中Z＜0的次数为nf次。根据概率论总的大数据定律中的Bernoulli定理知，N次独立试验中的失效概率nf/N收敛于该事件的概率pf，则失效概率估计值为：

结构的失效概率[7]可以表示为：

其中：I(x)是x 的指示函数。规定x ＜0 时，I(x)=1；x ≥0，I(x)=0。

根据式（16），X的第i个样本值为xi，则pf的估计值为：

刚性四杆机构输出角度可靠性的极限状态方程为：

其中：θmax为机构在运动过程中最大的输出角度值，θe为机构的最大允许角度输出值。

刚性四杆机构输出角可靠度[8]为主动杆件转动过程中最大的输出角在允许值范围内的概率，即：

3 算例

图1 为四杆机构的角度示意图，主动杆件转速为300r/min，L1、L2、L3、L4已知，具体值及分布类型见表1。

表1 弹性四杆机构的参数

如图1 所示，四杆分别为L1、L2、L3、L4，将机架AD 作为基准线，曲柄AB 能绕轴线360°范围内旋转，作为主动件带动整个机构运动。机构输出角为θ2，机构输出角为θ4，θ3为构件BC 的辐角。为了方便计算，将四杆机构中的B 点和D 点相连接，将四边形ABCD 分为两个三角形△ABD 和△BCD，设定∠DBC=φ，∠BDA=β，∠CDB=λ，BD=S。

根据四杆机构的角度几何关系得：

图1 四杆机构角度示意图

图2为基于蒙特卡洛方法对四杆机构输出角可靠性分析流程图。

图2 Monte Carlo 法输出角可靠性分析流程图

根据表1 机构变量参数表对参数抽取106个样本点，代入式（6）计算刚性机构输出角，并计算不同输入角下输出角的可靠性和失效概率，如图3和图4所示。

图中可以看出，主动杆件转速为300 r/min，输出角可靠度在主动杆件角度为0～60°达到最小值，120°～240°可靠性基本接近1，超过300°可靠性下降较快，通过计算可得到系统输出角度的可靠性为0.918 3。

4 结束语

弹性机构随着主动杆件转角的改变，输出角可靠度在主动杆件角度为0～60°达到最小值，120°～240°可靠性基本接近1，超过300°可靠性下降较快。由此通过计算可以得到弹性四杆机构中任意一点处的输出角随着主动杆件转动的可靠性，为后续机构的可靠性灵敏度分析打好基础。

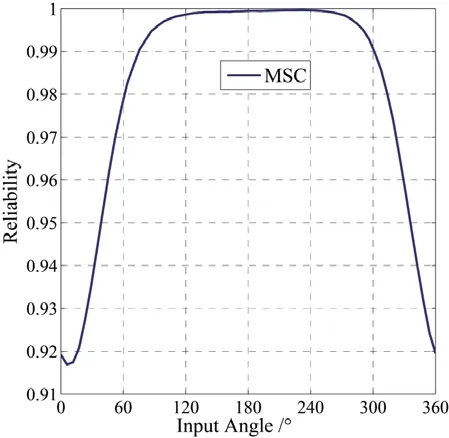
图3 输出角度的可靠性

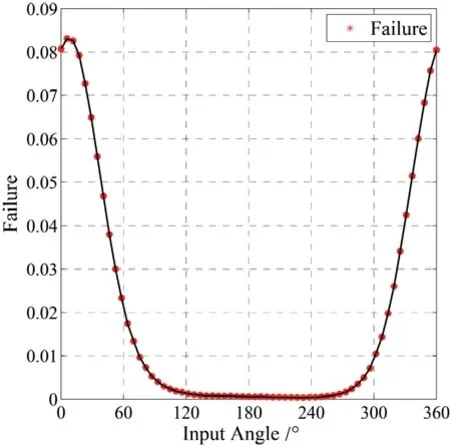
图4 输出角度的失效概率