水下机器人最优刹车轨迹规划设计
朱昱琛
(上海交通大学船舶海洋与建筑工程学院,上海 200240)
0 引言
轨迹规划问题实质为运动优化问题,通过进行轨迹规划能实现时间最短、能量消耗最少、路程最短等目标[1-3]。
目前进行轨迹规划的方法[4]主要分为两类:数值积分[5]方法与数值优化方法(包换动态规划[6]及凸优化[7]等)。数值积分法通常需结合最优控制的相关理论进行,进行数值积分时,通常将最优参数假设为“bang-bang”形式[8]。利用数值积分法进行轨迹规划时,其难点在于切换点的寻找问题[9]。相比较而言,数值优化方法求解较为简单。然而,采用凸优化解法时,可能因为轨迹规划问题的约束过多而无法将其转化为凸优化问题。另外,数值优化解法受到问题的复杂度及维数影响较大,当问题维数增加时,求解时间消耗将以指数方式增长[10]。
轨迹的光滑性[11]对于轨迹跟踪及实际执行等是极为重要的。通常而言,为获取光滑轨迹,在进行轨迹规划时需引入更多约束[12]。前人在进行光滑轨迹规划时,通常将轨迹约束定义为速度约束、加速约束及急动度约束[13]。而本文通过对水下机器人刹车运动的分析,将轨迹约束转化为推进器控制电压约束,从而使问题得到简化。
本研究在完成水下机器人最优刹车轨迹规划问题建模后,基于Pontryagin 极值原理与数值积分提出一种刹车轨迹规划方法。该方法相比于数值优化方法,能极大减少求解时间,具有较强实时性。
1 最优刹车轨迹规划问题建模
1.1 水下机器人垂向运动模型
为简化问题,本文仅研究水下机器人的垂荡运动,忽略转动及侧向平台影响,且运动过程,假定无外界干扰。水下机器人外形为近似四方体结构,该机器人上布置有8 个垂向推进器,并搭载着若干作业载荷,结构如图1 所示。

图1 水下机器人简图
以垂直向下为坐标轴正向,则水下机器人的垂荡方程为:

其中,w为垂荡速度,FT为垂向控制推力,△B为净浮力(经测定为恒为142.8 N),m为质量,Zw˙为附加质量,Zw和分别为一、二阶阻尼力系数。
定义水下机器人的总质量为M=(m-Zw˙),则可将方程转化为水下机器人模型参数如表1 所示。
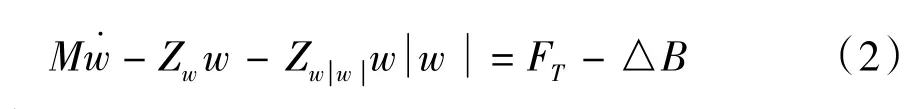

表1 水下机器人模型参数
水下机器人刹车上浮过程中,其制动力为流体阻力与推进器产生的垂向推力。假设垂向推力由N个完全相同的电动推进器产生。将单个推进器产生的推力记作T0,则有垂向推力FT=NT0。
推进电机动态方程为

其中R为电枢内阻,kcmf为感应电动势系数,k为电机减速比,J为转动惯量,kf为黏性摩擦系数。ω为电机角速度(rad/s),Vm为电机控制电压,该电压满足饱和约束。
推进电机模型参数见表2。

表2 电机模型参数
推进器中螺旋桨推力T0与转矩Q0为

其中,ρ为海水密度,D为螺旋桨直径,n为螺旋桨转速(rps)。推力系数KT(J0)和力矩系数KQ(J0)
可通过拟合为进速J0的线性表达式[14]:
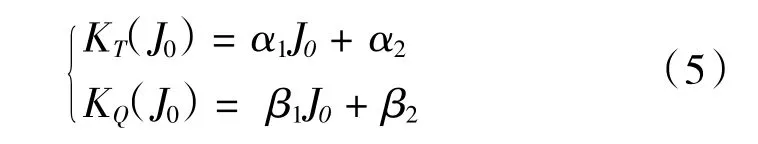
螺旋桨模型参数见表3。
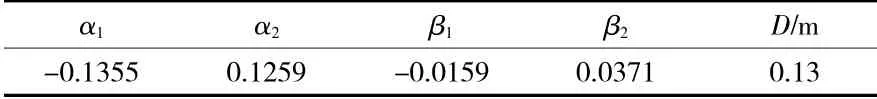
表3 螺旋桨模型参数
新定义参数如下:

经计算,新定义模型参数见表4。

表4 新定义模型参数
综上,可建立潜水器垂荡状态空间方程为:

假设悬停时的系统状态量为xf,控制输入为uf;此时x˙=0。则根据方程可得悬停条件如下:

1.2 轨迹规划问题建模
水下机器人开始运动时,满足x(0)=x0=(w0,0)T。假定此时水下机器人运动速度为,该参数已知。最优刹车轨迹规划问题可建模如下:

其中,T为潜水器开始运动时刻,该参数为未知常数。
轨迹起点z0未知而终点zf已知。可根据x1(t)的表达式与zf完成全过程轨迹规划。
2 最优刹车轨迹规划问题求解
本文采用一种基于Pontrygain 原理与数值积分的方式完成最优刹车轨迹规划,该方法简述如下。
根据方程,可建立Hamilton 函数为:


其中为Lagrange 算子。
根据Pontryagin 极值原理,最优控制输入u*需满足H(x*,u,λ*)≥H(x*,u*,λ*);则u*的形式为

根据方程,结合刹车过程的物理特性,可构造最优控制输入为:
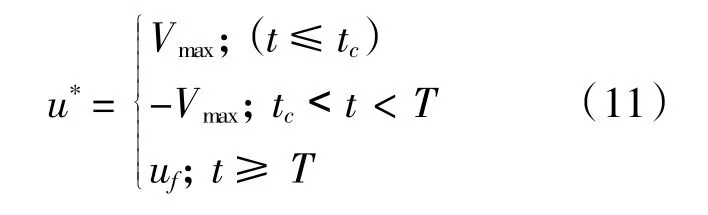
其中tc为未知常量。则最优刹车轨迹规划问题转变为控制电压切换时刻tc及停止时刻T的寻找问题,其中始末状态x0,xf已知。
当tc及此时的水下机器人状态量xc,则可基于数值积分完成T求解。因此,只需完成tc的搜寻即可。tc的搜索算法基于二分法与数值积分法进行,算法实现步骤见表5。其中,δt为极小时间常量。

表5 控制切换点搜索算法
3 仿真验证
基于表1~ 表4 的模型参数,初始条件为x0=(-2.31,0)T,终端条件为xf=(0,22.01)T。利用表5 所示算法解得切换点为tc=11.33 s。根据tc及xc进行数值积分可知T=11.355 s。仿真中,终端位置zf=25。最优刹车轨迹可根据水下机器人运动速度积分获取。根据公式进行仿真,结果如图1 所示。

图1 仿真结果
问题也可通过数值优化方法进行求解,例如可利用伪谱法将问题转化为非线规划问题,而后通过求解非线性规划问题进行求解。
本文利用MATLAB GPOPS-SNOPT 工具箱进行问题求解,对比结果见图2。由图2 知,尽管采用数值优化方法时,控制输入并非“bang-bang”形式。但最终所得的水下机器人速度变化基本一致,因此采用两种方法进行轨迹规划所得的最优轨迹相同。
但采用前述数值积分法求解时间只需数十秒,而采用GPOPS-SNOPT 工具箱求解耗时高达数十分钟。因此,本文提出的基于最优控制理论与数值积分法的刹车轨迹规划算法能在保证所得结果正确的前提下,极大减小求解时间。对比结果如图2 所示。


图2 对比结果
4 结束语
本研究针对水下机器人刹车上浮的运动特性,提出一种基于数值积分与最优控制理论的最优刹车轨迹规划算法。该算法相较于基于数值优化的方法,能极大降低轨迹规划所花费的时间,且不影响轨迹规划精度。
后续的研究将通过实物实验验证本文提出的轨迹规划算法可行性与最优性。同时,后续将考虑空间平动、转动影响,将本文的垂向轨迹规划推广至多维运动中。

