基于提高钻速的待钻井眼轨道设计方法

张洪宁,张建龙,覃德彪， 尹 强,袁 辉

(1页岩油气富集机理与有效开发国家重点实验室 2中国石化石油工程技术研究院 3中石化华北石油工程公司 4中石化胜利石油工程有限公司 5中石化经纬有限公司)

0 引言

在定向井及水平井钻井中，待钻井眼轨道的优化设计对精准中靶和优快钻井至关重要。目前涉及待钻井眼轨迹设计的基础方法主要有斜面法[1]、三维几何分析法[2]、简化方法[3]、无约束最优化方法[4]等，上述方法在设计过程中通常以最短井段或最小摩阻/扭矩为设计目标[5- 6]。但在工程实际中，井段最短或摩阻/扭矩最小，并不一定代表该设计轨道是最优的，井眼轨道设计的最终工程目标应是在满足钻井工程要求(如能否满足套管下入要求、摩阻扭矩、螺杆造斜能力等)的前提下，实现优快钻井。现有方法不仅在最优目标的选取上值得商榷，在工程适用性上，设计过程中经验性和随机性也较强,通用性和科学性均有待提升。

为此，本文在待钻井眼轨道设计时分段考虑了机械钻速的影响，以最短钻进时间为优化设计目标，建立了基于钻速预测的待钻井眼轨道设计方法，该方法可根据组合剖面的类型确定最优轨道设计参数，以保证设计出的待钻井眼轨道更利于优快钻井，更符合工程实际。

1 基础数学模型

在待钻井眼轨道设计时考虑机械钻速的影响，首先需预测螺杆钻具的造斜能力，确定滑动定向钻进和复合钻进的比例。为此，利用机械钻速预测模型，分段预测复合钻进和滑动定向钻进机械钻速，结合通用井眼轨道设计方法，明确钻井工程的限制条件，在确定选取剖面类型后，建立以最短钻进时间为优选目标的目标函数，确定轨道设计参数，具体计算流程如图1所示。基础数学模型主要包含螺杆钻具造斜能力预测模型、定向钻井机械钻速预测模型、不同剖面类型的轨道空间分布计算模型和钻井工程限制计算条件等。

1.1 螺杆钻具造斜能力预测

本文在预测螺杆造斜率能力时采用平衡趋势法预测螺杆钻具造斜能力[7]。该方法的基本思想为：造斜过程的实质是钻头与地层的相互作用并趋于平衡的过程，即当钻进趋势方向与实际钻进方向相同时，对应的井眼曲率即为螺杆钻具的造斜率，此时钻进趋势角[8]的计算公式为：

(1)

其中,w1=k11s1+k21s2+k31s3,w2=k12s1+k22s2+k32s3,w3=k13s1+k23s2+k33s3,s1=Ibircosαf+Ir(1-Ib)cosAafcosαa,s2=IbIrcosβf+Ir(1-Ib)cosAafcosβa,s3=IbIrcosγf+Ir(1-Ib)cosAafcosγa。

式中：Ib和Ir—分别为钻头和地层各向异性指数；Aaf—钻头合力方向与钻头轴向方向的夹角；αa，βa，γa—钻头合力矢量与坐标轴间的夹角；αf，βf，γf—钻进方向与坐标轴间的夹角。

图1 待钻井眼轨道设计流程图

假设某定向段的螺杆造斜能力为kdi，则定向与复合的比例关系如公式(2)所示。

Bi=kαi/(kdi-kαi)

(2)

式(2)中:Bi—第i井段滑动钻进进尺与复合钻进尺的比例关系;kαi—第i井段设计井眼曲率，(°)/30 m;kdi—第i井段底部钻具组合预测造斜能力，(°)/30 m。

1.2 定向钻井机械钻速预测

复合钻进状态下的机械钻速预测与常规钻速预测一致，按计算方式可分为三种：现场数据回归统计法、机械比能法和仿真分析法[9- 12]。为兼顾计算精度和最终目标函数的可解性，本文进行机械钻速预测的计算思路为：利用机械比能预测模型[13]，根据邻井资料，按加权平均的方式确定目标设计井的地质参数，然后根据机械比能预测模型反推机械钻速。具体推导过程见相关文献，在此不再赘述。

滑动钻进时机械钻速与复合钻进时的差异体现在转速、扭矩和钻压传递效率上。为此，利用公式(3)中表征钻头转速、扭矩和钻压传递效率对滑动钻进机械钻速的影响，C1为影响系数[14]。滑动钻进时的钻速预测公式为:

Rh=C1Rf

(3)

式中:Rh—滑动钻进时机械钻速，m/h;C1—钻压、扭矩和转速的整体影响系数，通常通过邻井资料获取，常用取值范围0.2～0.5。

1.3 不同剖面类型的轨道空间分布计算

待钻井眼轨道及空间坐标系如图2所示，在待钻井眼轨道AT上选取微元段dS，则该微元段的增量为:

(4)

(5)

图2 待钻设计坐标系示意图

将式(4)代入式(5)中，积分后可求出T点坐标为:

(6)

对于Z坐标可分为稳斜和变斜两种形式，对E、N坐标则可分为稳斜稳方位、稳斜变方位、变斜稳方位和变斜变方位四种情况。

通过式(4)～式(6)，利用公式变形和轨道几何学[15]便可计算出不同组合剖面类型时的待钻井眼轨道空间分布情况，如图2所示。

1.4 钻井工程限制条件

钻井工程对待钻井眼轨道工程要求主要是对井眼曲率的限制，设计的井眼曲率必须保证起下钻及下套管顺利，具体的限制条件[16]如式(7)～式(8)所示。

(7)

式中：Km—井眼曲率，(°)/30 m;Db—钻头直径，mm;DT—螺杆外径，mm;LT—螺杆长度，m;f—间隙值，mm，取值范围3～6 mm。

套管下入允许的最大井眼曲率：

(8)

式中：σo—井眼曲率，(°)/30 m;C1—安全系数，取值范围1.2～1.25;C2—螺纹应力集中系数，取值范围1.7～2.5;DC—套管外径，cm。

2 最优化设计数学模型

在确定待钻井眼轨道的剖面类型组合方式后，由式(4)～式(6)可确定靶点坐标与井斜角、方位角和段长的关系，假设设计剖面由i段组成，各段由S1、S2、Si表示,则以最短纯钻时间为优选目标的目标函数为：

(9)

其中最大狗腿度应小于套管下入允许的井眼曲率，约束条件为：

(10)

式(9)中:Tc—钻进时间，h;m—工具面调整次数;Tt—工具面平均调整时间，h，该数值根据邻井资料获取，取值范围通常为0.2～0.5 h。

在确定目标函数后，针对本文的具体问题，选用计算连续域的蚁群算法为优化设计算法，目标值为最短纯钻时间，蚁群算法[17- 18]作为一种仿生计算方法，通过模仿蚂蚁觅食时选择路径的行为原理，该算法具有计算速度快、收敛快的特点。

3 应用实例

JPHXX3井是位于鄂尔多斯气田的一口侧钻水平井，该气田的井型多为导眼井+侧钻水平井，通过钻导眼井确定A靶垂深，通过导眼侧钻的方式钻水平段。其中部分侧钻水平井采用的剖面类型为降—稳—增—平四段制剖面，该井眼轨迹设计方案重复定向工作量多、稳斜段控制难度高、复合钻进比例低，严重影响机械钻速和钻井效率。

JPHXX3井在完成导眼施工后，需对其侧钻后的待钻井眼轨道进行优化设计，该井侧钻后井眼轨迹设计起点为2 730 m，井斜为15.24°，方位为346.27°，优化前井眼轨迹如表1所示。

由表1可知，优化前的待钻井眼轨道采取先降斜再增斜，以较小的稳斜角完成稳斜段钻进，以确保靶前位移充足，以较小的设计造斜率钻至A靶点，确保摩阻扭矩小、套管下入安全。但该设计由于过于依赖现场施工人员经验，过度考虑钻井工程的需求，存在设计局限性：①需先降斜后增斜，重复定向工作量多；②稳斜难度大，需反复定向降斜，定向工作量多。

为此，利用本文方法对待钻井眼轨道进行了优化设计，根据现场工程实际，将待钻井眼的剖面选取为增斜稳方位+增斜变方位+增斜稳方位+稳斜稳方位四段制，优化后的井眼轨道如表2所示。

表2 JPHXX3井优化后井身剖面设计表

由表2可知，按照上述方法优化设计的井眼轨道，造斜率增高，可提高复合比例，提高钻井效率，通过设置增斜变方位段，更利于实际工程实践和矢量中靶。

为了分析优化设计前后井眼轨道的差异，利用上文中建立的机械钻速预测模型对两类井眼轨道的机械钻速、复合比例和钻进时间进行了对比，如表3所示。

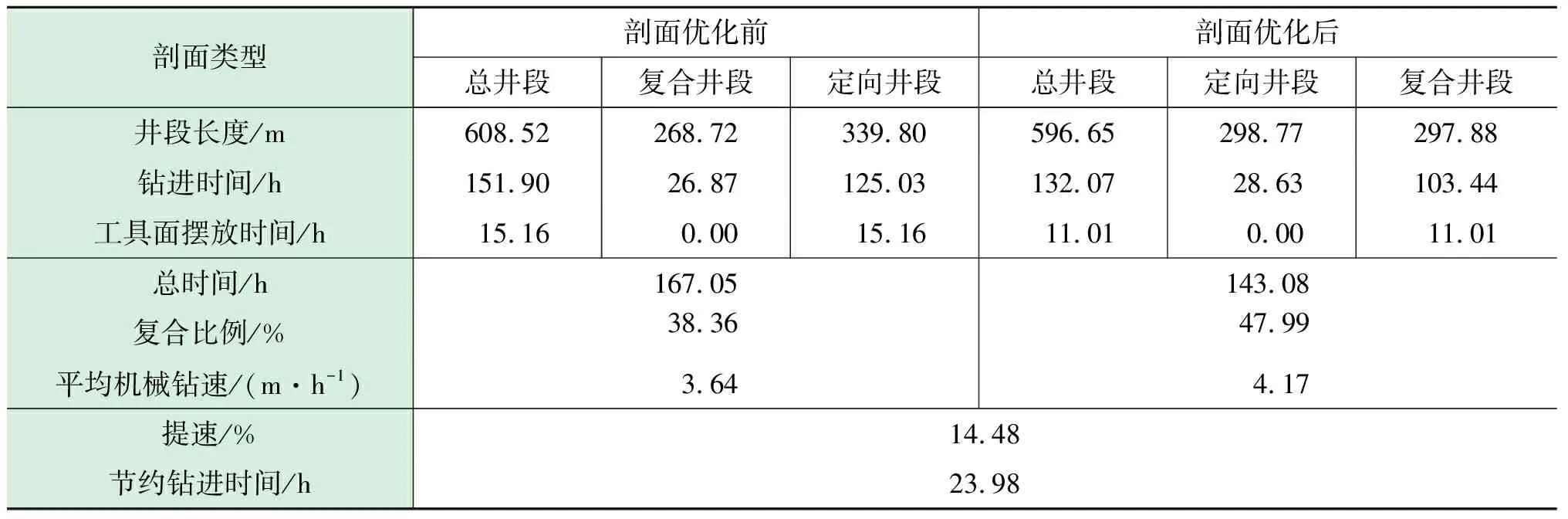
表3 井身剖面优化前后机械钻速、复合比例和钻进时间对比表

对比结果表明：优化后的井眼轨道理论复合钻进比例可达49.53%，较邻井提高19.3%，同等钻速条件下可较邻井节省钻进时间约24 h，并且使该井具备了由侧钻点至A靶点“一趟钻”的提速潜力，摩阻在10 t以内，满足钻井工程需求。

4 结论

(1)根据待钻井眼轨道选取的组合剖面类型，利用待钻井眼轨道设计方法确定最优轨道设计参数，更符合工程实际，提高了待钻井眼轨道设计的实用性。

(2)将最短钻进时间设置为优选目标，建立分段考虑定向钻井机械钻速的目标函数，在满足钻井要求前提下，可保证设计出的待钻井眼轨道更利于优快钻井，提高了待钻井眼轨道设计的科学性。

(3)现场应用实例表明，本文研究得到的待钻井眼轨道设计方法可有效提高复合比例，缩短钻井周期，并且可满足钻井工程需求。