运用斜交分解法巧解类抛体运动问题

刘二虎 郑慧玉

(江苏省泗洪中学,江苏 宿迁 223900)

类抛体运动是中学物理中常见问题,主要通过运动的合成与分解来求解。其中,正交分解法是最常用的分解方法,即将速度和加速度分解到两个相互垂直的方向上,形成各自独立的直线运动。正交分解法形式固定、易掌握,但计算较为繁杂。斜交分解是将运动依据速度和加速度的特点,分解形成两个彼此独立、互不垂直的直线运动,可简化计算过程,方法更加巧妙，以下探讨几类利用斜交分解法处理的类抛体问题。

1 重力场中的一般抛体运动

例1：如图1所示,小球以初速度v0在距离地面高度为h的位置向上斜抛，求抛射的最大水平射程。

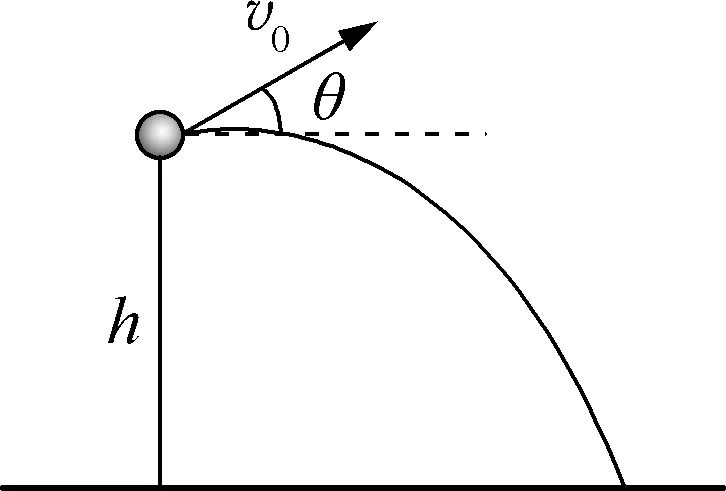
图1

解析:这是典型的重力场中抛体运动问题,用正交分解法解题时，将运动分解成水平方向的匀速直线运动和竖直方向的竖直上抛运动,通过联立两个运动方向上的方程,把水平位移写成关于抛射角度的函数，进而求极值。

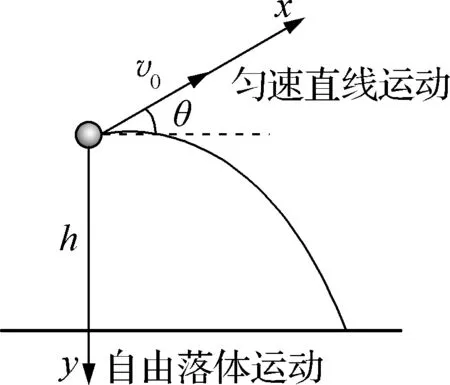
图2

图3

小结:利用斜交分解法避开了较为复杂的函数极值求解,将水平位移巧妙过渡到速度的矢量三角形运算上,计算简洁，在利用斜交分解法时需要透彻理解矢量运算和运动的独立性。

2 静电场中的类抛体运动

例2：如图4所示,在绝缘光滑平面上有与桌面平行,大小恒为E的匀强电场，图中实线为电场的等势面，一带正电、电量为q的小球从A点释放。已知小球初速度为v0,方向与BC平行,过B点的等势线与BC的夹角为30°,AB与等势线垂直,AB=BC，求小球到达C点时间t。

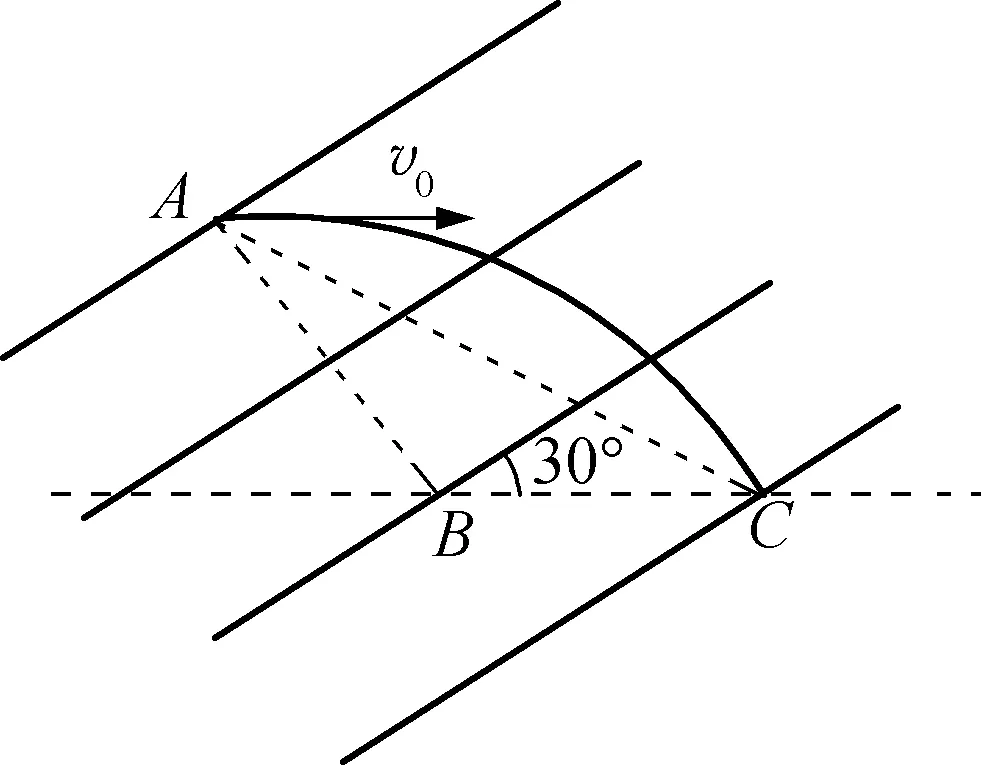
图4

解析:这是常见的带电小球在静电场中做类抛体运动问题,如果运用正交分解法,小球在水平方向上做匀减速直线运动,在竖直方向上做匀加速直线运动,通过联立两个方向上的运动方程来求解。

根据小球速度和受力特点,可以将运动分解为沿着初速度方向的匀速直线运动和沿着电场力方向(即AB方向)的初速度为零的匀加速直线运动(图5)。通过斜交分解后的两个运动形式更简单,处理起来也更为简便。

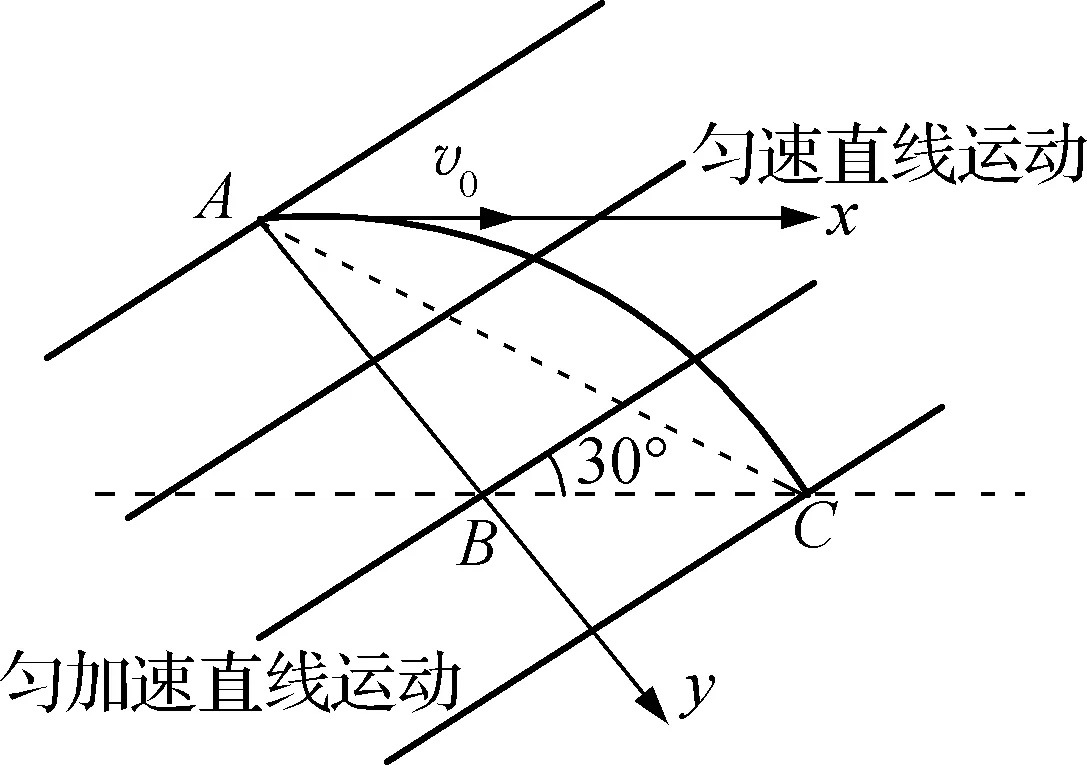
图5

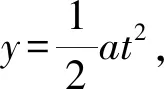
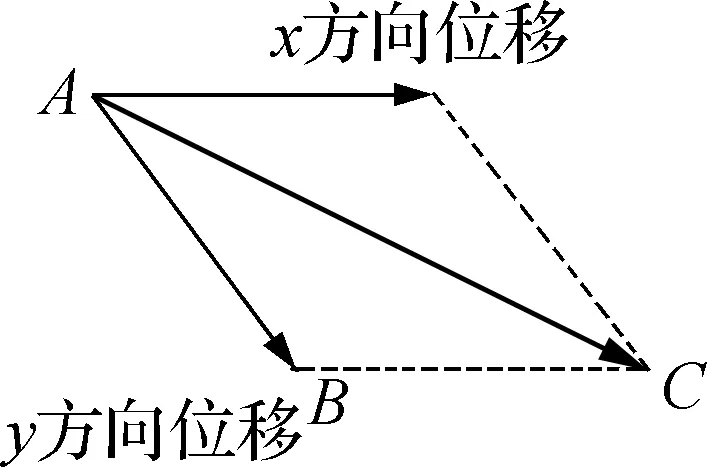
图6

小结:采用正交分解法时，两个分运动都是初速度不为零的匀变速运动；而利用斜交分解，能将运动分解成两个更为简单的运动,结合分运动和合运动的位移关系,能更快解决问题。运用斜交分解法处理这类问题时明显更为巧妙,避开了较为繁琐的计算。

3 重力场和静电场相叠加的类抛体运动

例3：如图7所示,在水平面上有一个带负电的小球,电荷量为q,在平面上有平行地面的水平向右、大小为E的匀强电场,小球在空中以水平速度v0抛出,若小球足够高,求小球落地前的最小速度和时间。

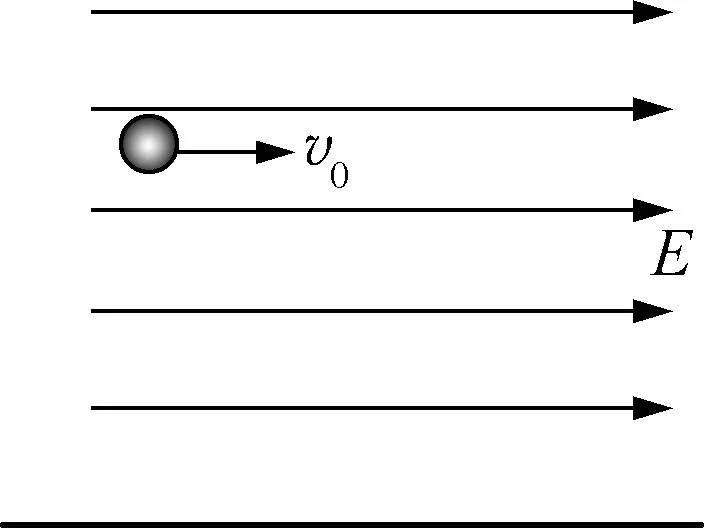
图7

解析:运用正交分解法，小球的运动可分解为水平方向上的匀减速直线运动和竖直方向上的自由落体运动,利用两个分速度可求得小球运动过程中速度和时间的关系,再进行临界值的求解，而运用斜交分解法可以将求解过程简化。

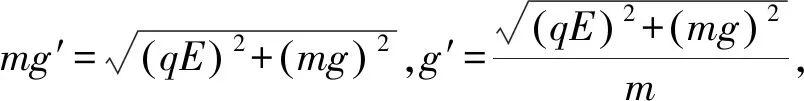
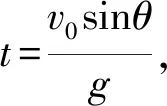
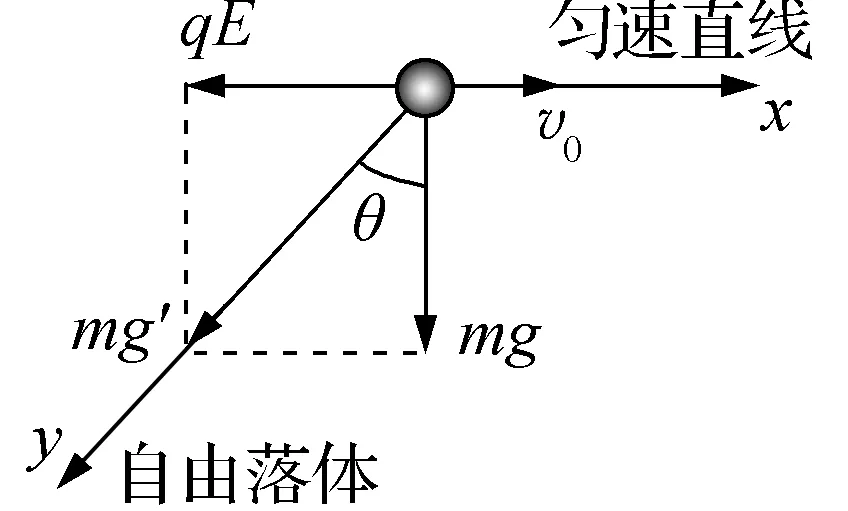
图8

图9

小结:运用斜交分解法后，小球的运动变为匀速直线运动和等效自由落体运动的合成,分运动的形式比用正交分解法更为简单，从而能更加巧妙地找出速度最小时所对应的物理状态。

4 变阻力作用下的抛体运动

例4：如图10所示,质量为m的小球在地面上一定高度水平抛出,平抛的初速度为v0,在重力和空气阻力的作用下经过一段时间落到地面上,已知落地时速度方向和水平面的夹角为θ,空气阻力f=kv,求落地时的速度大小v。

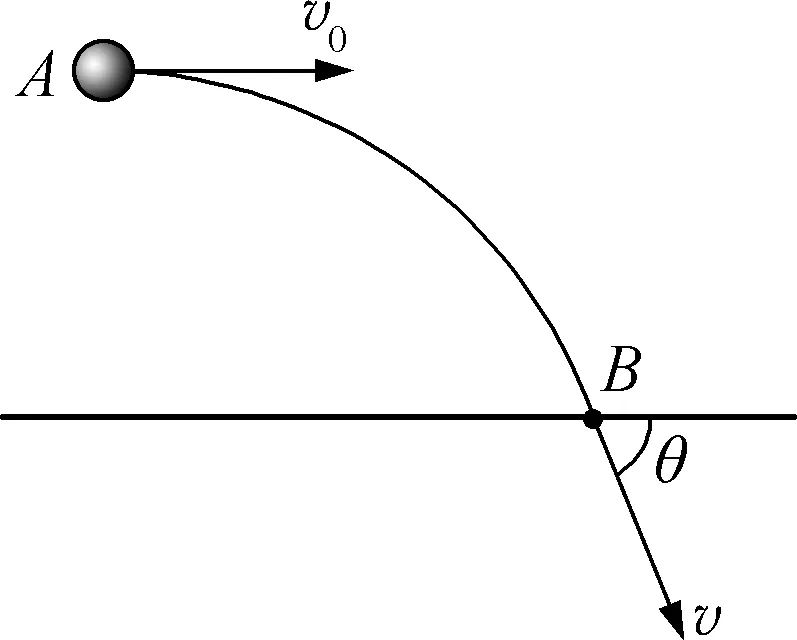
图10

解析:小球在抛射的过程中除了受到恒定的重力的作用外,还受到一个大小随速度变化的阻力的作用。若运用正交分解法,小球在水平和竖直两个方向都受到一个变化的阻力作用,导致两方向上的加速度都不是定值,求解较为复杂，采用斜交分解法可以避开变化的阻力,简化计算过程。

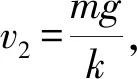
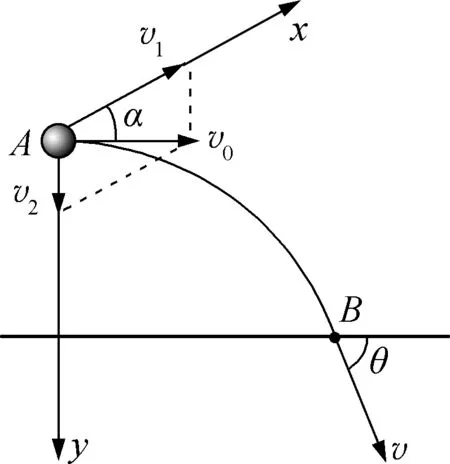
图11

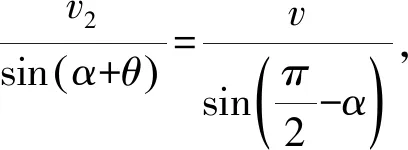
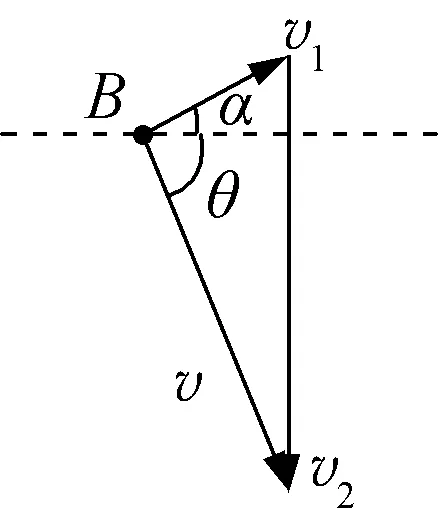
图12

小结：对于这类变阻力问题，在运用斜交分解法构建两个分运动时,通过补偿特定大小的速度，使重力平衡竖直方向上的阻力,从而将这个方向的分运动变成速度大小已知的匀速直线运动，由此来实现对速度矢量的求解,巧妙地将复杂的变加速问题进行简化处理。

5 结语

从重力场、静电场、复合场以及变阻力四种情形下类抛体运动的典型问题的解析可以看出：正交分解对运动分解的“门槛”相对较低,但常常要解析两个方向的运动,处理起来相对繁琐。而运用斜交分解法时能从速度和加速度两个角度出发,分解为更易处理的分运动,往往可以分解出一个匀速直线运动或初速度为零的匀变速直线运动。运用斜交分解法，在计算上更多地利用位移、速度矢量三角形,能更加巧妙地解决问题。