基于正交分析的地铁目标频段隔振排桩参数研究

姜博龙

(中国铁路设计集团有限公司城市轨道交通数字化建设与测评技术国家工程实验室,天津 300308)

排桩屏障被认为是轨道交通环境振动路径隔振中的一种有效方式，因而被广泛研究[1-3]，其隔振效果影响因素包括桩径、桩间净距、土层与桩的材料参数、桩长、桩的布置范围、桩的埋深与地铁埋深的相对关系等。近年来，周期结构带隙理论被引入到排桩隔振的研究中，为目标频段的隔振排桩设计提供了理论基础[4]。

大量学者围绕目标频段隔振的周期排桩展开研究。黄建坤[5]将该问题简化为二维平面应变问题来研究体波的传播衰减规律，进行了无限周期假设和周期边界处理，求解得到桩-土周期系统的频散关系，揭示了首阶完全带隙随桩径、桩间距、桩与地层材料参数等因素的变化规律；刘心男[6]将三维有限元计算结果与二维平面应变模型计算结果对比，发现随着桩长的增加，二者计算结果逐步接近；蒲兴波[7]提出了全新的面波频散曲线识别方法；另外，还有部分学者围绕复阻尼周期排桩[8]以及饱和土条件下周期排桩[9]展开研究。目前，已有原理性实验验证了周期排桩带隙分析理论的正确性[10]，证明在采用无线周期排桩求解的带隙频率范围内与之对应的有限周期排桩会对振动产生大幅衰减；另外，地铁-地层-周期排桩三维有限元模型被建立来预测设计排桩在相应带隙频段内阻隔地铁振动的效果[11]；此外还有研究涉及优化选型方法[12]等。

目前隔振排桩隔振效果研究中针对地下隧道振源的、可以设计调节隔振频段的研究并不多。基于带隙特性的周期排桩设计频段内的隔振性能研究主要分为无限周期排桩带隙特性和有限周期排桩传输衰减特性。由上述分析以及表1可以看出，在带隙特性研究中广泛采用的无限周期、无限桩长假设，明确了带隙随桩径、桩间净距、桩与地层材料的变化规律，但是对桩长、桩的布置数量以及振源与桩相对位置关系等问题研究得不够充分，而这些因素将直接决定计算带隙范围内振动的实际衰减情况，包括排桩屏障后有效衰减区域以及不同区域的振动衰减水平。此外，上述因素对隔振效果影响的强弱顺序、设计取值亟需参数化分析，提供相应的理论依据。本文基于正交理论[13]、带隙理论和数值模型，针对地下振源，对影响有限周期排桩带隙范围内振动衰减效果的因素进行参数研究，包括桩排数、桩列数、桩长、桩到地铁水平距离、桩与地铁埋深相对位置关系等，获得各因素作用主次顺序以及在某种典型地层条件下的建议取值。

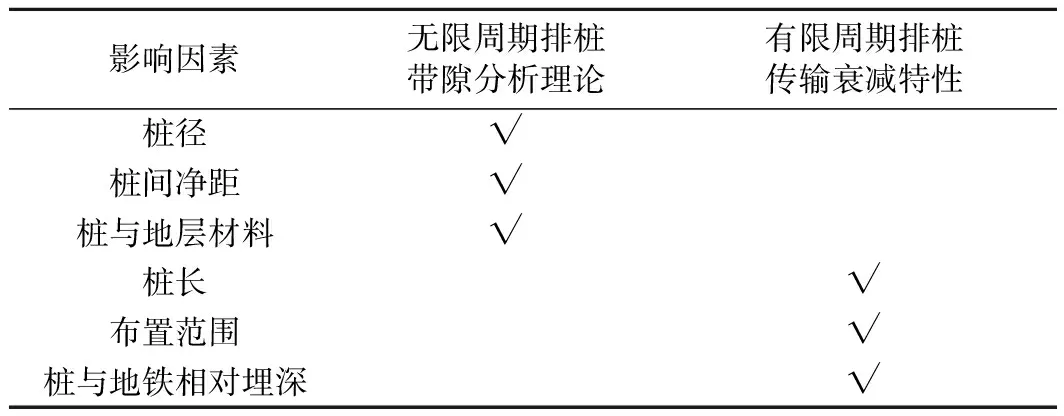
表1 排桩影响因素及对应研究方法

1 周期排桩频散计算的平面波展开法

1.1 平面波展开法

平面波展开法[14]可用于求解周期排桩带隙特性，其基本假设包括无限周期假设和无线桩长假设，此时振动在排桩-土层中的传播可视为平面应变问题，并解耦为平面内问题和出平面问题。不失一般性，波动方程可表示为式(1)的形式

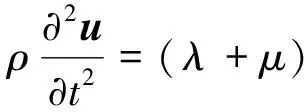
(1)

式中,ρ为密度；λ和μ为拉梅常数；u为位移矢量；uj表示位移分量。

其中,u=[ux，uy，uz]

j=x，y，z

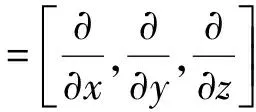
由于排桩的周期性排列，密度ρ和拉梅常数λ和μ可按照傅里叶级数展开为

(2)

式中，G1为倒格矢；r为位置矢量。

其中，f=ρ(r)，λ(r)或μ(r)，r=(x，y，z)

根据Bloch-Floquet理论，位移解可展开为：

(3)

式中，K为波矢；G2为倒格矢；ω为角频率；u(r，t)为位移矢量。

把方程(2)和方程(3)代入方程(1)，可得到本征方程

(4)

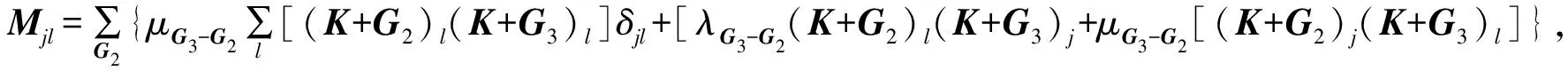
G3=G2+G1;

i，j，l=x，y，z。

对于散射型排桩，傅里叶系数可表示为

(5)

其中，

η=(πR2)/S

(6)

式中，η为单个基本单元中桩的占比；P(G1)为结构函数；S为典型单元面积；J1为第一类第1阶贝塞尔函数。

使波矢K扫掠第一不可约Brillouin区，即得到排桩-土体体系的频散曲线和带隙。

1.2 计算算例

排桩布置形式及基本单元见图1，其中，a=4 m、R=1.2 m、r=0.8 m。粉质黏土(图1(b)中A)密度为2 010 kg/m3，动弹性模量为308 MPa，动泊松比0.327，阻尼比0.03，压缩波速472.6 m/s，剪切波速235.0 m/s。桩体的材料参数见表2。计算带隙如图2所示。

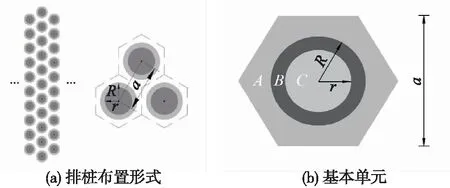
图1 排桩布置形式及基本单元

表2 排桩材料参数

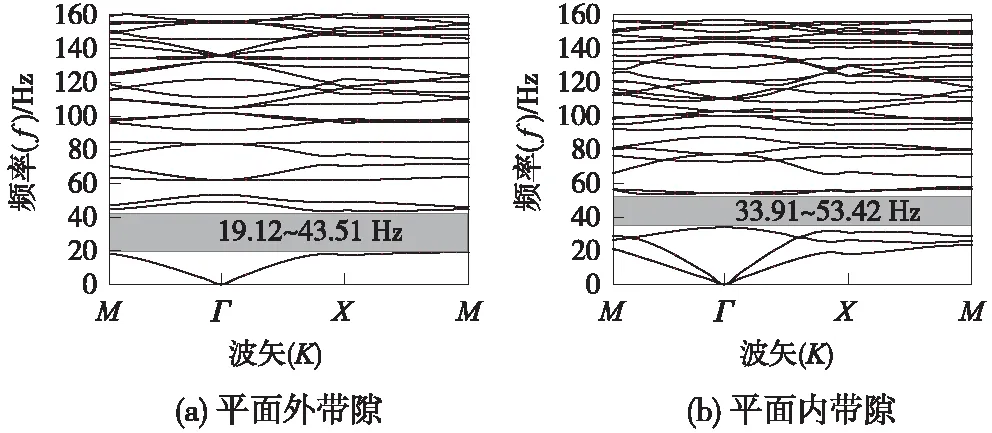
图2 带隙分布

2 采用正交分析的参数研究

由上文可知，对于桩-土周期系统的带隙分布直接相关的参数包括桩径、桩间距、桩与土的材料参数，文献[5]已对其进行了参数化分析。由于带隙分析采用了无限周期、无限桩长的基本假设，因此，忽略了桩长、列数、排数、排桩到隧道水平距离、隧道埋深等5个因素影响，本文采用正交分析方法对这5个因素展开参数分析。本文正交分析所采用的土体信息、桩的排布形式与参数取自上文计算算例，带隙分布见图2。

2.1 相关因素选定

设计带隙频段内振动衰减水平以及屏障后衰减的有效空间受桩长、列数、排数、排桩到隧道水平距离、隧道埋深等5个因素影响。因此，本节开展5因素、4水平的标准正交分析。

2.2 确定水平

根据周期带隙理论，每一排隔离桩对振动都有一定的衰减作用，随着周期复现，最后达到对某些频段完全滤波的目的，从而形成带隙，即桩排数越多，隔振效果越好。然而，考虑工程实际的施作空间及成本限制，很少见到5排及以上排桩，故本次正交分析中桩的排数选取的4个水平为1、2、3、4排。

列数并无严格的限制，本文采用的4个水平为10、8、6、4列。

根据《铁路隧道设计规范》[15]和《地铁设计规范》[16]，振源深度的4个水平选取为0 m(地表情况)、6 m、12 m、18 m，其中0 m为地表振源、6 m为常规浅埋隧道，二者具典型性，其余水平按照增量原则设计。

桩长取1～6倍隧道埋深，并按照等差递增，桩长设计为12，24，30，36 m。

依照《环境影响评价技术导则—城市轨道交通》[17]，7.5 m是环境振动的一个转折距离，将其设为排桩到隧道距离的一个水平。压缩波VP、剪切波VS、瑞利波VR波速关系[18]如式(7)所示

(7)

可得本算例中土层瑞利波速VR=204.9 m/s，关心频段(带隙)介于20～80 Hz，土体波长LR介于2.25～10.245 m。泊松比μ=0.327<0.35，隶属较硬土质，排桩到振源距离r=1.0LR，特征因数ar=2π[19]。

因此，选取排桩到隧道的水平距离为2，7.5，15，22.5 m，远近场均有涉及。

2.3 选用正交表

正交分析采用标准正交表L16_4_5，即5因素4水平共16次试验。根据因素与水平，给出有限元计算的具体方案，见表3。

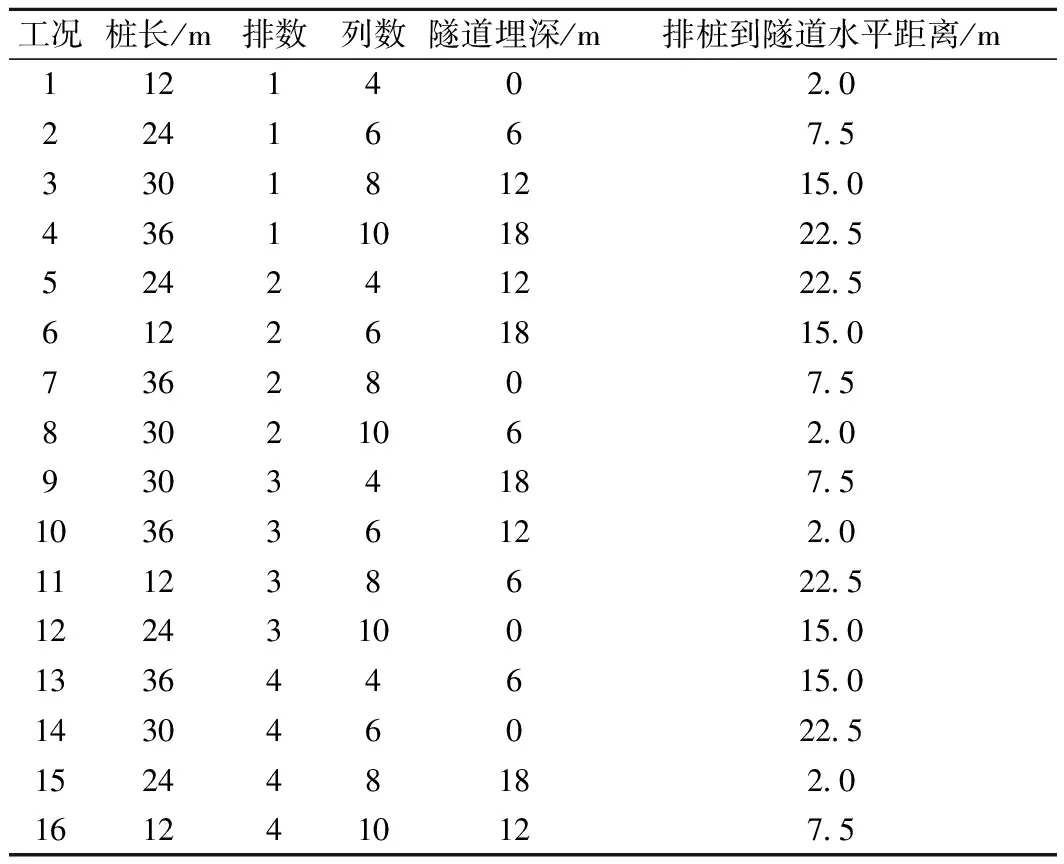
表3 正交分析计算工况

2.4 实施方案

按照设计的正交工况，每组工况计算有桩和无桩两个模型，参数设置相同。

首先，建立隧道-土体-有限周期排桩动力有限元空间模型。由前文可知，首阶带隙主要分布在19～54 Hz频段，土体剪切波速为Vs=235 m/s，故λs，max=12.37 m，λs，min=4.35 m。当荷载位置到边界距离D=1.5λs，max=18.56 m时位移收敛结果较好，当网格尺寸R=λs，min/6=0.725 m时，除靠近荷载0.5λs，min=2.175 m距离外，其余位置计算结果较为理想。本文计算模型范围取为85 m(长)×40 m(宽)×36 m(高)，振源距左边界18 m，隧道内外径分别为5.4，6 m，基底厚0.36 m。左边界网格尺寸为1 m，隧道与排桩区附近网格尺寸取0.5 m，其他部分采取过渡尺寸网格。按照16种工况的设计参数建立16个模型，并建立16个对应的无桩模型对比，共计32个模型。图3给出了工况16有桩条件下计算模型。

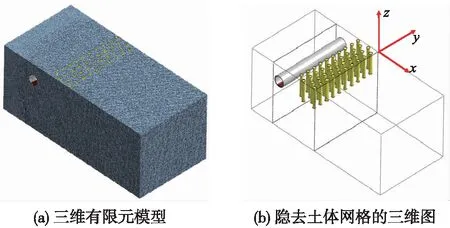
图3 正交分析中工况16的三维有限元计算模型

土体阻尼比取0.03，分析频率1～100 Hz。瑞利阻尼常数α和β分别为：α=0.37，β=9.46×10-5。采用弹簧阻尼边界来解决动力分析中截断边界的波动反射，按照法向和切向两个方向添加。因仅考虑排桩隔振效果与带隙范围内的隔振表现，模型采用脉冲荷载作为激振输入，可节约计算时间且不影响减振效果随参数变化的作用规律，具体时程和频谱参见图4，力的作用点为隧道内道床板上表面的中心点，如图5所示。

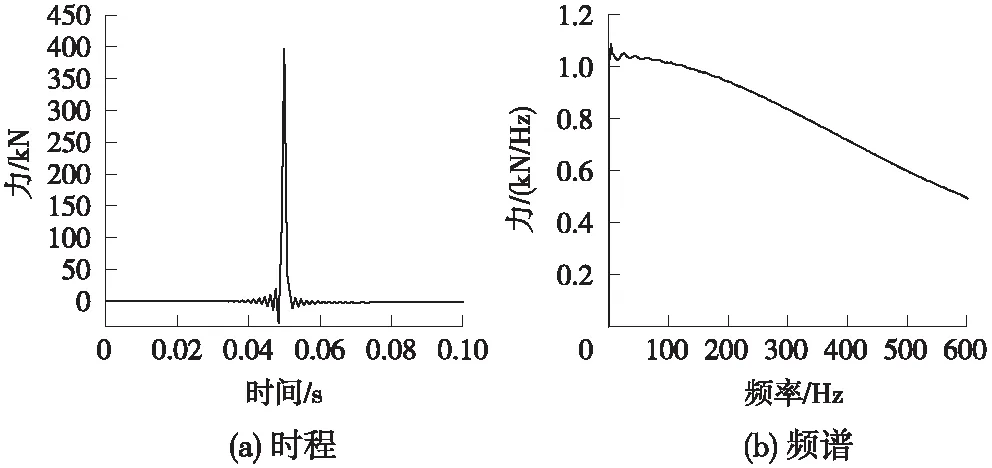
图4 激励力的时程和频谱

图5 激励力作用点

2.5 分析指标

本研究的评价量应能够同时反映带隙频段振动衰减水平以及有效衰减区域两项结果，故定义有限周期排桩首阶带隙中心频率处的分析指标ER作为评价量

(8)

其中

Arn=a有桩/a无桩

式中，δn为桩后区域某点无桩条件下的加速度响应；δp为桩后区域某节点有桩条件下的加速度响应；SR为积分域，即桩后有衰减的区域；Sn、S为节点所占面积；Arn为节点振幅衰减系数；a有桩为减振工况下排桩后节点的振动加速度响应；a无桩为未设置隔振排桩的对比工况下相同位置节点的振动加速度响应；n为节点数。

评价量ER综合反映隔振排桩后区域内有效衰减范围和衰减水平两项内容，ER越大表明衰减效果越佳。本文对桩后地表一定范围进行振动提取，考虑边界效应，提取范围与边界保持一定距离，取40 m(y方向)×45 m(x方向)，如图3所示。计算该范围首阶带隙的中心频率振幅衰减系数，将其绘制成云图，由云图求解评价量ER，分析评价量ER随各因素的变化规律。

2.6 结果分析

(1)直观分析

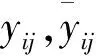
Ri=max[yi1，yi2，…]-min[yi1，yi2，…]

(9)

表4给出了16组正交工况中竖直方向的ER，表5给出了竖直方向ER的极差Ri，并将竖直方向ER结果绘于图6，极差Ri绘于图7。水平方向亦同，仅给出极差结果，绘于图8。由图7和图8可知，各因素对竖向振动衰减影响的主次顺序：隧道埋深>桩长、排数>列数>排桩到隧道的距离；对水平向影响的主次顺序：排桩到隧道距离>隧道埋深、排数>桩长>列数。

表4 各工况竖直方向ER计算结果 m2

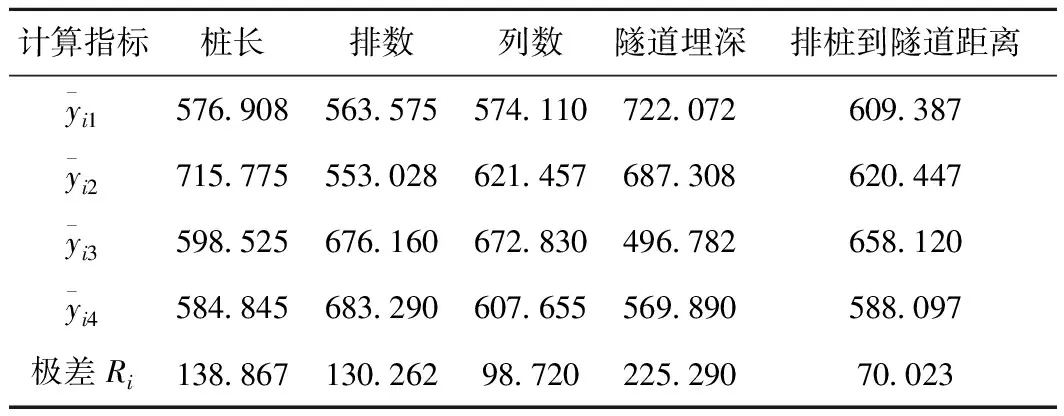
表5 指标ER竖直方向影响因素极差分析结果 m2

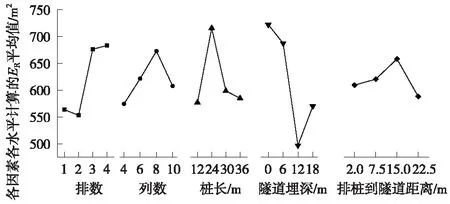
图6 竖直方向效果曲线

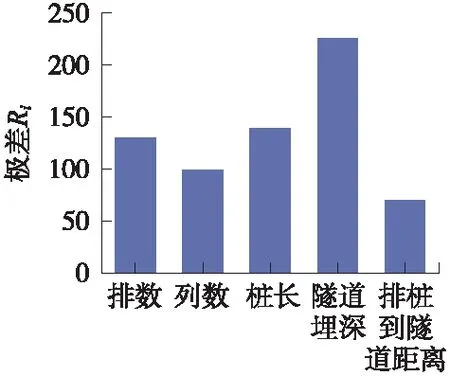
图7 竖直方向极差柱状图

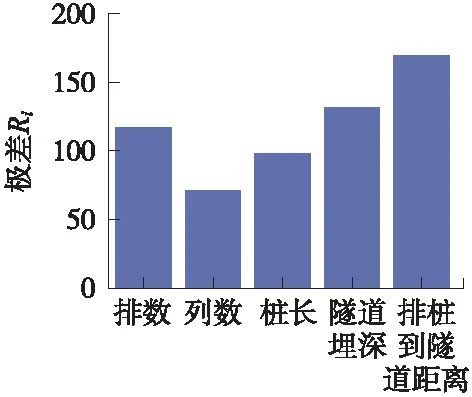
图8 水平方向极差柱状图

(2)方差分析

方差反映数据离散程度，可衡量试验条件稳定性，根据Fisher偏差平方和加和性原理，在偏差平方和分解的基础上依托F检验法，对影响效果及其交互效果进行分析，此方法称为方差分析[20]。将方差分析结果列于表6和表7，并将F比值绘于图9。

表6 竖直向方差分析

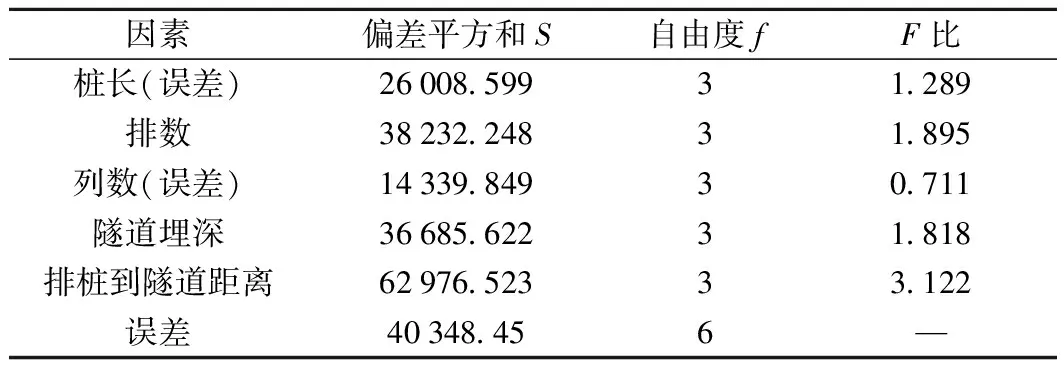
表7 水平方向方差分析

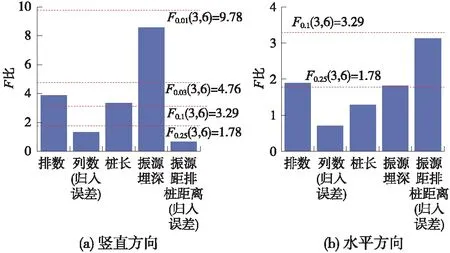
图9 F比

根据方差分析理论，由表6、表7和图9可知，在竖直向，隧道埋深对隔振效果的影响最显著；水平向无显著性影响因素，但相对来说排桩到隧道距离影响较大。

竖直方向，各因素对隔振效果影响排序为：隧道埋深>排数>桩长>列数>排桩到隧道距离；水平方向顺序为：排桩到隧道距离>排数>隧道埋深>桩长>列数。这与直观分析结果一致。

(3)交互分析

交互作用指因素的联合作用对结果的影响，它表征因素间相互促进或相互抑制的作用[20]。正交分析中，交互作用记作A×B，原则上交互作用应当作一个因素看待。为研究直观分析和方差分析中显著因素(竖直方向包括振源埋深、排数、桩长，水平方向包括振源距排桩距离、排数、振源埋深)间两两因素的交互作用，故拆分成多张3因素2水平标准正交表，其中第3个因素为前2个因素的交互作用。如当排数参与交互作用分析时，可选水平组合为(1排、2排)或(2排、3排)或(3排、4排)的3种方式，便可覆盖全部水平。

两因素交互有3×3=9种组合，表8和表9分别给出竖直方向排数-隧道埋深交互分析的9种组合中1种的设计表和极差结果，图10给出了结果柱状图。涉及其他因素组合时情况类似，在此不再赘述，仅将主导因素汇总表整理给出，详见表10～表15。分析过程中，为使体波传播规律不失一般性，有关长度、距离物理量全部以带隙中心频率所对应的土体的体波波长λ作为参照量进行无量纲化，给出相对桩长、相对距离及相对埋深。其中，竖直方向以首阶带隙中心频率fV=31 Hz对应土体SV波长λSV(λSV=VS/fV=7.58 m)为参照量；水平方向同理取土体的SH波长λSH(λSH=VP/fH=10.74 m)为参照量。

表8 竖直方向隧道埋深(0、6 m)与排数(1、2排)交互作用极差分析结果 m2

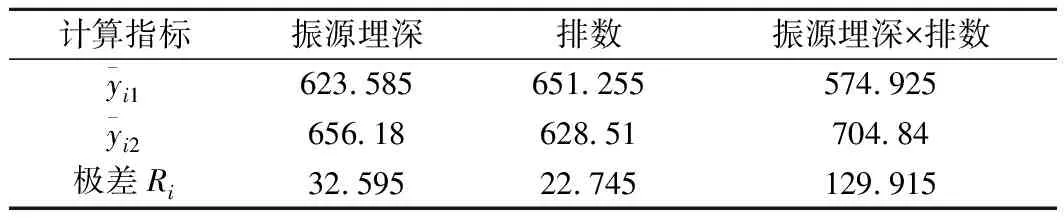
表9 竖直方向隧道埋深(0、6 m)与排数(1、2排)交互作用极差分析结果 m2

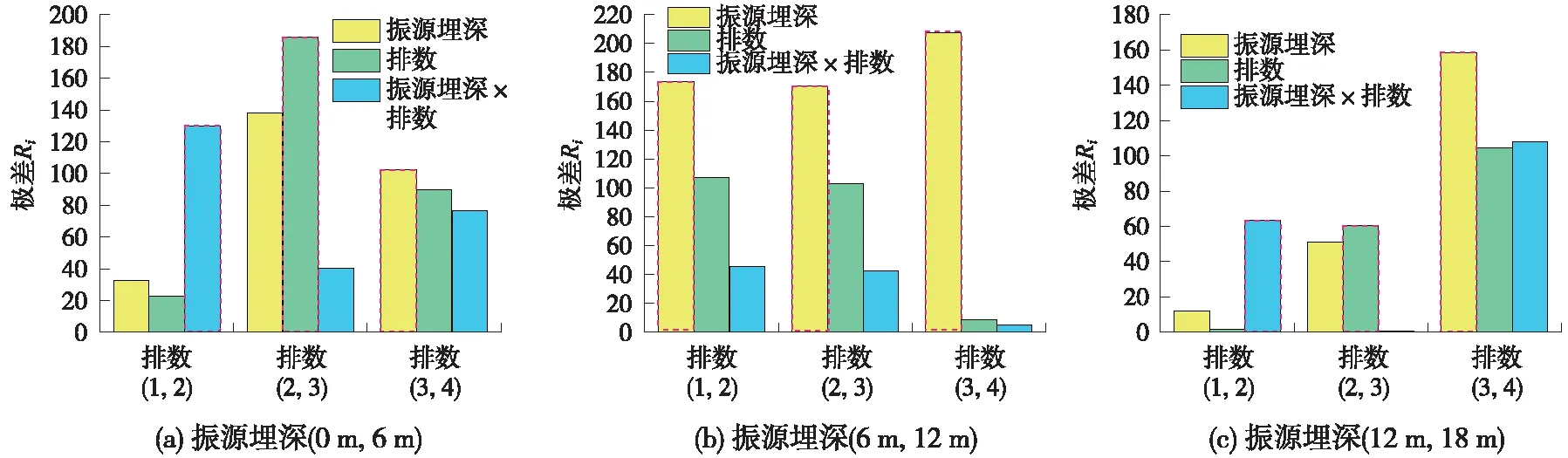
图10 竖直向振源埋深和排数的交互作用极差

表10 竖直方向隧道埋深-排数交互主导因素

表11 竖直方向桩长-隧道埋深交互主导因素

表12 竖直方向桩长-排数交互主导因素

表13 水平向隧道埋深-排桩到隧道距离交互主导因素

表14 水平向排数-排桩到隧道距离交互主导因素

表15 水平向排数-隧道埋深交互主导因素

分析表8～表15，考察桩排数，为取得较好的竖向衰减效果，排数可以考虑增加到3排，继续增加排数改善效果不显著；在距离隧道0.7λSH～2.1λSH区间内布设排桩时，增加排数衰减效果改善明显；1.4λSH～2.1λSH范围内增加桩排数到3排就可以获得较好的水平向衰减，在0.7λSH～1.4λSH范围内增加到4排效果更佳；当隧道埋深为0.56λSH～1.12λSH时，增加排数，水平向衰减效果改善明显，4排效果最佳。

考察桩长：隧道埋深不足0.8λSH时，桩长达到3.2λSH即可取得较好的竖向隔振效果；隧道埋深处于1.6λSH～2.4λSH时，在1.6λSH～3.2λSH和4λSH～4.8λSH范围内增加桩长可有效改善竖直方向隔振效果。

考察排桩到隧道距离：为取得较好的水平向衰减，隧道埋深为0～1.12λSH时，宜采用近场隔振，在距隧道0.7λSH以内设置排桩，效果更显著；隧道埋深1.12λSH～1.68λSH时，不宜采用近场隔振，在距振源1.4λSH以外布置排桩可取得更好的水平向隔振效果；在近场(0.186λSH～0.7λSH)隔振时增加排桩到隧道距离可改善水平向隔振效果。

3 结论

在粉质黏土地层条件下，针对地下振源、频段可调的排桩隔振屏障，基于带隙理论和正交分析理论，研究桩长、排数、列数、隧道埋深以及排桩到隧道距离等因素对振动衰减效果的影响规律，研究结论如下。

(1)各因素对竖向振动衰减影响主次排序：隧道埋深>桩长、排数>列数>排桩到隧道距离。

(2)各因素对水平振动衰减影响主次排序：排桩到隧道距离>隧道埋深、排数>桩长>列数。

(3)为在竖直方向带隙范围内取得良好振动衰减效果，建议如下：隧道埋深<0.8λSV时，桩长取3.2λSV；隧道埋深介于1.6λSV～2.4λSV时，在1.6λSV～3.2λSV和4λSV～4.8λSV范围内增加桩长；排数达到3排就能取得较为稳定的隔振效果。

(4)为在水平方向带隙范围内取得良好振动衰减效果，建议如下：距离隧道1.4λSH～2.1λSH范围内设置排桩，采用3排桩可以取得较为稳定的隔振效果，其他距离建议增至4排；隧道埋深为0～1.12λSH时，距振源0.7λSH以内范围布置排桩；隧道埋深处于1.12λSH～1.68λSH时，在距隧道1.4λSH以外布置排桩。