成对点云对应关系优化的点云配准算法
梁 宏
(江西理工大学 土木与测绘工程学院, 江西 赣州 341000)
三维点云配准问题是计算机视觉[1]、逆向工程[2]和三维重建[3]等领域的一项关键技术,在三维物体的激光扫描测量中,为了完整地表示该物体详细信息需要从不同角度对物体进行扫描,因此必须对多组点云数据进行配准来得到完整的点云。本质上是通过计算基准帧与非基准帧的变换矩阵,把非基准帧的坐标系转换到基准帧的坐标系下。
快速精确的点云配准是三维建模研究的热点和重点,目前已有多种解决点云配准问题的算法。Besl等[4]提出了迭代最近点算法(ICP),它是目前应用最广最为经典的配准算法,中外学者提出了一系列改进[5-7],这些算法在点云变换的幅度较小时配准精度较高,但是对配准初始条件要求较高,否则容易陷入局部最优。因此,研究学者大多先采用初始配准获得良好的初始配准位置,再采用ICP算法进行精确配准。目前,通过扫描对象表面的局部几何特征寻找点云间点与点对应关系是目前点云配准的研究热点之一。常用的 3D特征描述子有旋转图像(spin image)[8]、点特征直方图(PFH)及改进的快速点特征直方图(FPFH)[9-10]、旋转投影统计(RoPs)[11]等,但对于稠密的点云,计算每个点的特征描述子常与特征点相结合。陆军等[12]根据不同邻域半径估算的法向量的方向偏差选择特征点,并依据点云多法向量邻域特征进行配准;舒程珣等[13]将点云转化为深度图像,再利用卷积神经网络进行配准;胡修祥等[14]结合 NARF 特征点与 FPFH 特征描述子获得良好的初始位置,再利用 3D-NDT 进行精确配准;曾繁轩等[15]提出了基于曲率特征结合ICP的配准算法。这些方法描述性强,但是稳健性较差,易出现错误的对应点对,且计算复杂,配准效率低。
基于以上情况,为了提高点云配准的精度和效率,提出一种基于成对点云点云对应关系优化的快速点云配准方法,通过建立点云的对应关系,对对应关系进行优化,通过交替优化的方式来求解点云的变化姿态,从而实现对点云的配准。实验结果表明,与其他算法相比,本文算法配准精度较高,速度较快。
1 基于成对点云对应关系优化的点云配准
1.1 问题提出
给两个曲面点云A、B,目的是找到一个刚性变换矩阵T,使得A、B两个点云能够完美对齐。采用一种针对A、B对应关系进行稳健的优化。这些对应关系通过执行FPFH特征匹配来建立优化。但是,在优化过程中不会重新计算点与点的对应关系,因此这种优化必须要处理一些错误或者虚假的对应关系,如图1所示。
图1 一对有对应关系的表面点云
1.2 对应关系优化
为了生成初始的对应点集L,使用了快速特征点直方图(FPFH),选择该特征是因为它可以在0.01 s内计算出来,并且可以在广泛的数据集中提供良好的匹配精度。定义F(A)={F(a),a∈A},其中F(A)是针对a点计算的FPFH特征,同理定义F(B)={F(b),b∈B}。采用最近邻搜索查找初始的对应点集,即对于每个点a,在F(B)中找到F(a)的最近邻点,对于每个点b,在F(A)中找到F(b)的最近邻点,组成初始对应点集L1。仅仅只通过最近邻点来生成初始点集,此时L1的误差非常高。采用两次优化来削弱误差。首先,特征优化原则,即对应点(a,b)需满足a的最近点是b并且b的最近邻点是a,此时对应点就满足了距离最近原则,优化后得到的点集记为L2;其次对应优化原则,即参考点云特征点之间的L2范数与待配准点云对应点之间的L2范数之比需满足以下关系:
(1)
式中,λ=0.9,对应点满足这个关系之后就认为这两个对应点是完全对应的,通过优化之后得到的点集记为L3。
1.3 优化原理
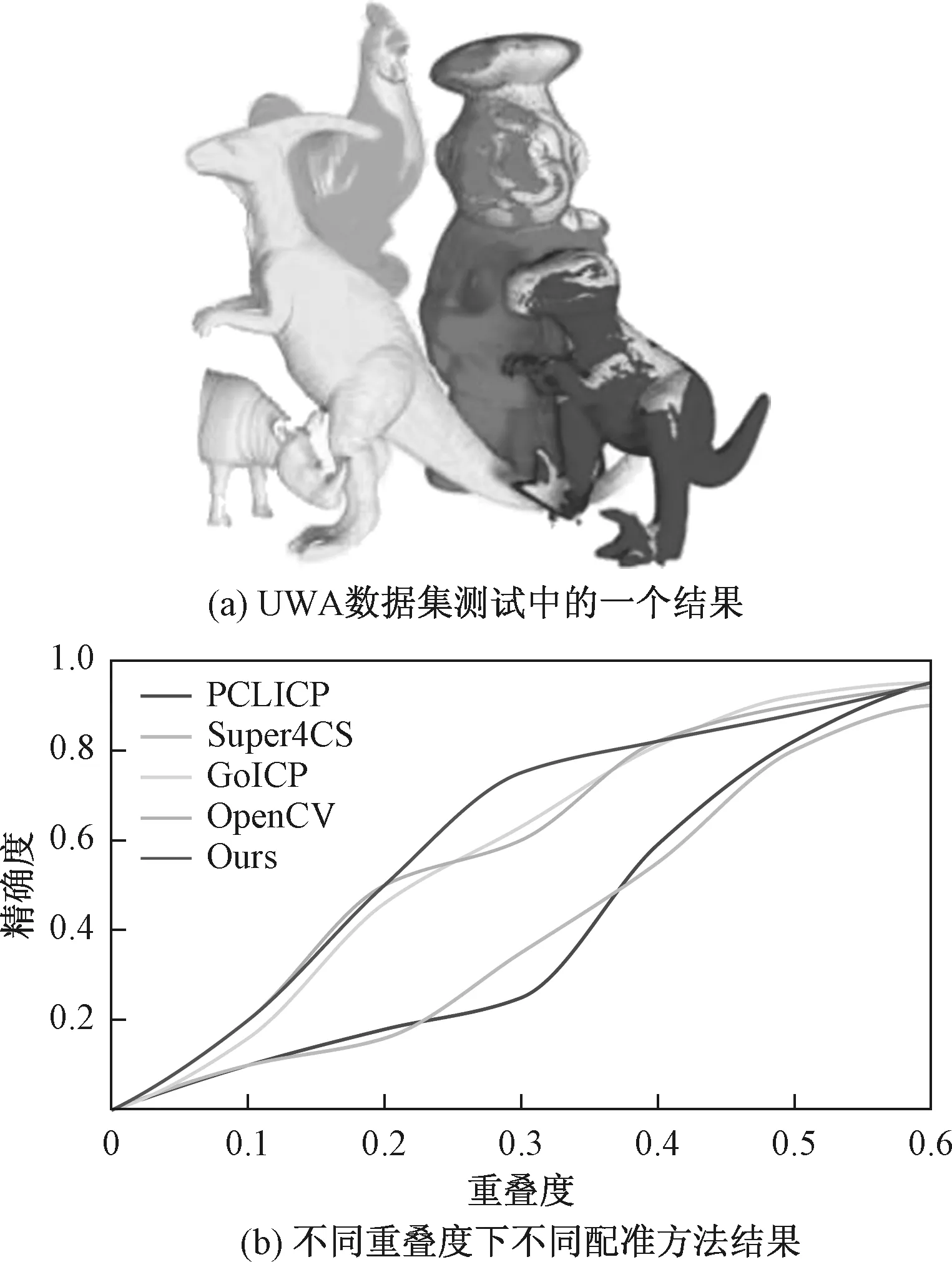
给定一组表面点云{Qi},i=1,2,3,…,n,估计一组转换姿态T组成一个矩阵,使这个矩阵将这些点云在全局坐标系中对齐。首先为重叠区域每对点云(Pi,Qi)经过对应点优化后构造一组候选对应关系rij,i (2) 该函数要实现对错误的点云对应关系进行优化,令Kp,q为对应关系上的处理函数,此时要求解的目标函数变为 (3) 式中, (4) 为了使得加入的处理函数不会影响点云转换姿态T,因此,令函数对变量函数求导后为0,即 (5) 解得 (6) 为了求解该函数的最小化问题,采用交替优化来解决该问题。首先对函数进行优化,根据式(4)、式(5)进行优化,为了简化该问题,实际应用时令μ=1。当把Kp,q优化完成之后,接下来对所有的变换姿态T进行最小化。 首先根据最小L2范数的原则,使得成对点云满足它们之间对应距离最小,通过把变换姿态线性化成6个分量τ=(ωi,ti)=(αi,βi,γi,Δxi,Δyi,Δzi),其中ω、t分别为旋转分量和平移分量。把T通过τ的局部线性函数可近似表示为 (7) 此时目标函数(2)只跟Ti有关系,然后通过高斯牛顿迭代法求解非线性模型的回归参数,可得到 (8) 式中,Jr为雅可比矩阵,其中的元素为目标函数对Ti的一阶偏导数;r为残差。 可以通过非齐次线性方程组的求解方法解出τ,此时得到了点云姿态的6个分量。最后通过Eigen库把这6个分量转化成一个4×4的变换矩阵,再随机选择几组点云,检验这几组点云是否能够完美对齐。 该优化方法一共只有两次循环,而且每次只更新转换的矩阵和残差。其中,建立两个点云的线性关系只需执行一次。在进行迭代之前,需要一次性建立两个点云的k-d树,通过优化的最近邻搜索,增加搜索的速度。其他的计算复杂度与优化算法的迭代次数有关。基于k-d树结构,为Pi个点建立对应关系的复杂度为O(lgPi);为Pi个点更新残差的复杂度为O(lgPi)。假设最大迭代次数为n,则针对循环过程中一对点云的姿态优化算法。可给出表1所示的复杂度分析结果。 表1 复杂度分析结果 为了验证本文方法的有效性,实验采用公开4个数据集进行测试和验证,并且采用三维扫描仪实地采集的点云数据模型进行测试。刚体优化的算法采用C++语言编写,在Visual Studio 2017的开发环境下编译。所有程序均运行在一台内存为32 G,主频为3.6 GHz的四核台式电脑上。 该算法的时间和精度验证通过对点云进行一系列的控制实验。为了进行控制实验,使用公开的数据集中的Bunny、Angel、Lion、Statue点云数据模型和实地采集到的数据Room模型。为了进一步比较本文算法与其他配准算法的配准性能,对5组点云采用不同算法进行20次配准,得到了平均配准误差和配准时间,如表2所示。由表2的实验结果可知,通过4种算法在5种不同的模型上进行实验得到了点云匹配的标注差(RMSE)。通过4种配准算法在不同模型上配准需要的时间t上可以看出,本文算法运行效率是在PCL-ICP以及Scale-ICP算法之上的。跟ICP算法相比,本文算法耗时降低了约60%;跟Scale-ICP算法相比,本文算法耗时降低了50%;跟Sparse-ICP算法相比,本文算法耗时降低了20%左右,同时配准的精度与它们相当。Lion配准图如图2所示。 为了验证本文算法是否解决了已收敛到局部最优的问题,改变点云初始状态,通过旋转与平移改变配准点云的初始位置,结果如图3所示。进行了两组实验,在PCL方法中,对其进行了初始化,在理想情况下时,本文算法可以相当于这些局部修正方法的精度。但是当初始位置偏离过大(旋转20 °或者平移点云直径的10%)时,局部方法的精度会降低。相反,本文算法在所有条件下都具有相同的精度。 表2 不同算法点云配准对比 图2 Lion配准图 图3 局部收敛性对比结果 为了验证本文算法在不同的重叠度下的点云配准精度,对UWA数据集进行测试,数据集总共包含188个成对测试。结果如图4所示,现有的配准算法在此数据集的性能较差。本文算法实现了85%的精确率,与GoICP和OpenCV相当(分别为82%和78%),PCL和Super4PCS的精确度都低于50%。 算法的鲁棒性是衡量算法在有噪声或异常的情况下是否能够进行精确匹配,利用公开的Angel数据验证该方法在不同噪声水平下的鲁棒性。实验中,将3组不同的均匀噪声:①σ=0无噪声;②σ=0.002 5的随机噪声;③σ=0.005的随机噪声随机的加入到Angel模型中。为了消除随机性,该方法在不同的噪声水平进行了15次蒙特卡洛独立测试,并记录了各种方法的运行时间和配准误差。表3给出了各种方法在加入了随机噪声后的配准结果。 图4 测试结果 表3 不同噪声下各种点云配准方法结果 首先通过FPFH生成初始点集,根据最邻近原则对点集进行筛选生成初始的对应关系,在根据L2范数比值去除错误的对应关系,实现点云的精确配准。选取了几个代表性的点云模型进行试验得出以下结论: 1)提出的成对点云对应关系优化的配准算法能够使旋转角度较大、初始距离较远的两点云配准时不易收敛到局部最优,能够实现全局配准 2)本文算法对比其他算法,在确保精度的同时,在迭代次数与配准时间上更具有优势,同时对噪声大、重叠度低点云配准也具有较好的效果。 今后考虑在点云对应点寻找前添加对点云颜色纹理特征的寻找,提高点云匹配的精度,从而提升对应点集的精确性,最终提高配准速度。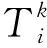
1.4 复杂度分析

2 实验结果
2.1 实验对比

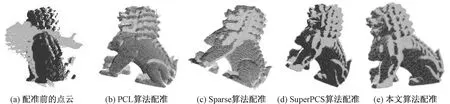

2.2 重叠度与鲁棒性分析

3 结论

